一類具Holling Ⅱ型功能反應的食餌-捕食者模型的定性分析

范學良,雒志學,張宇功

(蘭州交通大學 數理學院,甘肅 蘭州 730070)

自然界中普遍存在的物種間相互作用是一種基本關系為捕食者-食餌的關系,揭示具有功能反應的捕食者-食餌相互作用的關系具有十分重要的意義和價值,許多學者對此已經做了大量的研究工作.

對于兩種群相互作用的具有功能反應函數食餌-捕食模型，人們往往關心的是系統是否有孤立的周期解,換句話說就是系統是否有唯一的極限環,因為穩定的極限環對應穩定的種群的生態平衡.穩定的平衡態對種群的生存具有重要的意義.

文獻[1]研究了具有Holling Ⅰ 型(它適用于藻類,細胞等低等生物)功能反應函數的捕食者-食餌系統：

(1)

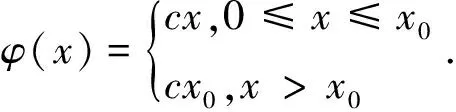
(2)

時,對系統的平衡點及極限環進行討論.其中ω,a,b,k,r,α,β為正常數,l符號不定.

首先作時間變換(1+ωx)dτ=dt,則系統(2)變為

(3)

(4)

1 平衡點的性態

結論1 在平面上l<0或br-al<0時,系統(4)只有平凡平衡點O(0,0)及非平凡平衡點B(x1,0);當l>0且br-al<0時,系統有3個平衡點.

為了方便下面引理的證明，首先給出幾點說明：

若線性系統在平衡點A處的特征方程為λ2+pλ+q=0,如果特征方程有2個異號的實特征根那么平衡點為鞍點,若特征方程有2個同號的實根那么平衡點為結點,若特征方程中的p>0,q>0則結點是穩定的.如果p<0,q>0則結點不穩定.如果特征方程有一對共軛復根,則平衡點為焦點.如果特征方程有一對純虛根那么平衡點為中心焦點.詳見文獻[7].

結論2 在R2平面上,O(0,0)是鞍點,當al-br<0時,B是結點,當al-br>0時,B為鞍點;當l>0,al-br<0時,B為穩定的結點.

證明為了討論平衡點的類型,首先將系統線性化,分別求出系統(4)對應點處的雅克比矩陣：

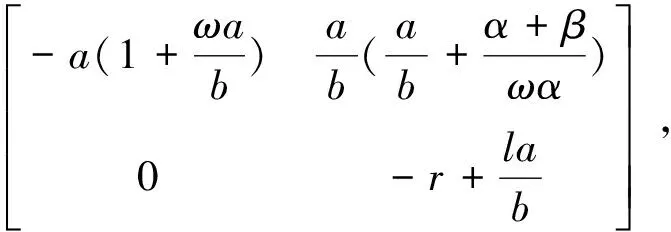
又當B點為結點時所對應的特征方程為……