一種控制增益函數未知的自適應模糊控制

張明君，邵 誠，李世寬

（1.大連理工大學 控制科學與工程學院，遼寧 大連 116024；2.大連大顯集團，遼寧 大連 116620）

0 引 言

模糊自適應控制近20年得到了快速發展，在非線性系統控制領域得到了大量應用［1－13］.目前，模糊自適應控制主要分為基于模糊建模規則的間接自適應控制和基于模糊控制規則的直接自適應控制［2］.間接自適應控制中，模糊系統的語言描述能力被充分用來描述系統，從而使系統中的未知函數可以用模糊模型來建模，文獻［3－5］為典型的模糊間接自適應控制.但是對于較高變量維數的系統，或當模糊模型的規則數增加時，上述文獻中的控制器計算量將會增長迅速.而直接自適應控制通常采用模糊系統去逼近理想的等價控制器，一般要求系統增益函數已知，或者其界值可估計，但實際應用中界值不易確定，這樣可能使控制器的設計過于保守.文獻［6－8］中的直接模糊控制方法均需已知控制增益函數；文獻［9－11］中均假設控制增益為常數；文獻［12－13］中控制方法則是在估計未知控制增益函數界值的基礎上設計的，可能使控制器設計具有保守性.

本文在文獻［13］基礎上，針對含有不確定項的非線性系統，在控制增益函數及其界值均未知的條件下，僅要求控制增益函數為有界函數，設計新穎的等價控制器，應用廣義模糊雙曲正切模型在線逼近等價控制器，并用一個雙曲形式的魯棒補償控制項來消除系統中的不確定項和逼近誤差，以期實現魯棒直接自適應模糊控制.

1 預備知識

廣義模糊雙曲正切模型［14－16］是近年由Zhang等提出的模糊模型，已被證明是一種萬能逼近器.

定義1［15］已 知x＝（x1（t） …xn（t））T為MISO系統的狀態向量，通過平移常數dzj（z＝1，…，n，j＝1，…，wn）構成廣義狀態變量＝xz－dzj，定義模糊集合P和N的隸屬函數分別為

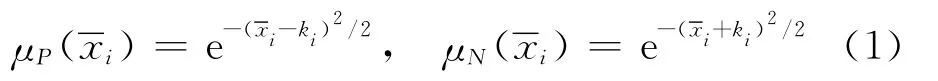
式中：ki為常數.模糊模型的模糊規則（第l條）為

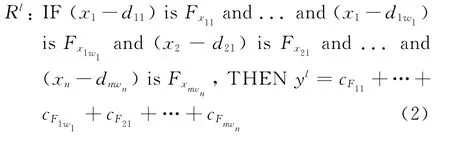
其中Fxzj為廣義狀態變量＝xz－dzj的模糊子集，cFzj是與之對應的常數.系統的輸出變量y（t）由各模糊規則推得為

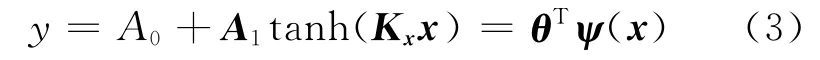
2 控制問題描述

考慮如下形式的SISO 非線性系統：

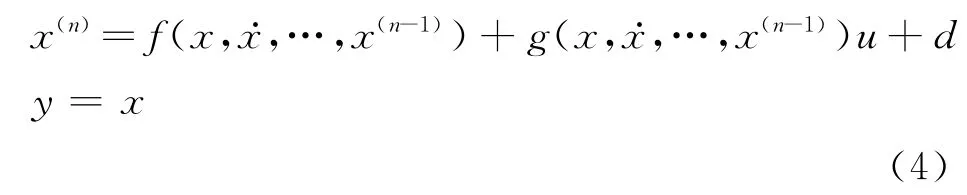
其中f（x）、g（x）是未知的非線性函數；系統的輸入、輸出變量為u（k）∈R，y（k）∈R，狀態向量為x＝（x…x（n－1））T＝（x1…xn）T∈Rn，系統的不確定項d∈R有界，包含外部干擾、未建模動態和測量誤差項，

假設1［17］非線性系統（4）中的非線性函數f（x）和控制增益函數g（x）未知但有界，即x∈Rn，存在未知邊界使得成立.

假設2［17］對于任意x∈D，有g（x）／xn＝0，使得

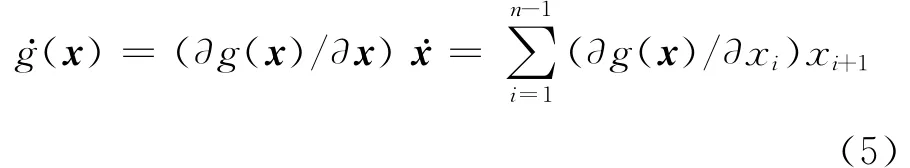
其中D∈Rn表示模糊逼近域，也即（x）只取決于狀態向量x.

控制系統（4）的設計目標是，設計一個控制算法，使系統輸出y（t）跟蹤有界參考信號ym（t）.定義e＝ym－y為系統的跟蹤誤差，假設ym具有n－1 階的各階導數，定義系統（4）等價表示為

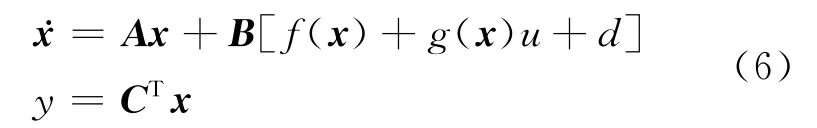
3 魯棒直接自適應模糊控制算法

由文獻［1］知，當f（x）和g（x）均已知，d＝0時，對于系統（6）可設計等價控制器

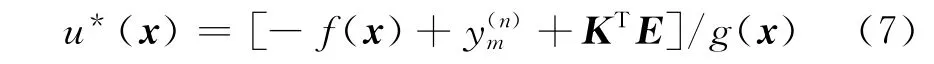
其中K＝（kn…k1）T∈Rn使得h（s）＝sn＋k1sn－1＋…＋kn的所有的極點均落在左半開平面上，即A－BKT為嚴格Hurwitz的.

假設Q為滿足Q＝QT＞0的正定對稱矩陣，P是滿足下列方程的正定解：

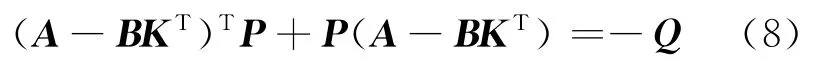
本文對上述控制器修改如下：

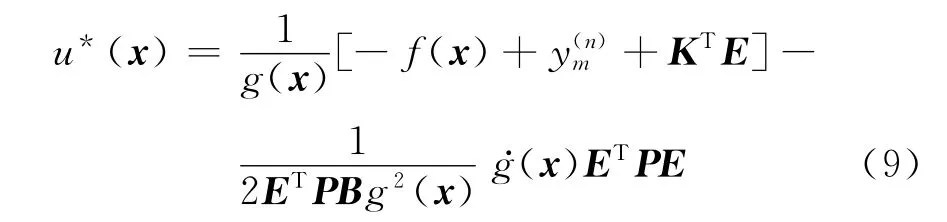
因為f（x）和g（x）均未知，且d≠0，用廣義模糊雙曲正切模型在線逼近上述模糊控制器

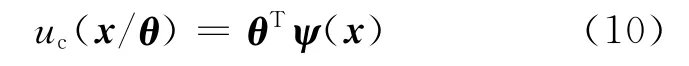
注釋1 在線逼近等價控制器的模糊模型可以采用模糊基結構的多種模糊模型.本文選用廣義模糊雙曲正切模型逼近模糊控制器有如下原因：首先，GFHM 已被證明是萬能逼近器，可以用來構建模糊控制器；其次，其模糊語言簡單易獲得，而且模型的數學表達式簡單，算法易實現［15］.

定義自適應參數θ的約束集為Ωθ＝｛θ∈Rl：θ≤Mθ｝.定義最優參數向量和參數誤差向量分別為

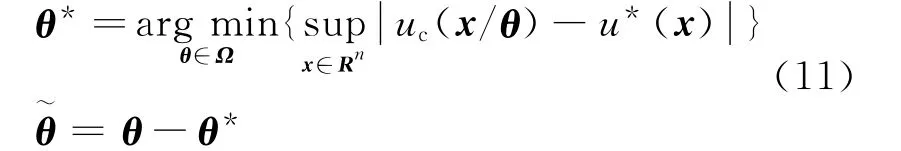
模糊控制器的最優逼近誤差表示為wf＝g（x）［u＊（x）－uc（x／θ＊）］.設計系統（6）的總體控制器如下：

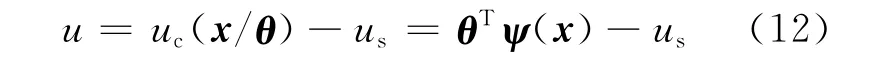
其中的魯棒補償控制項us在后面給出.注意，此控制器表達式中無控制增益函數g（x）或函數的界值，克服了設計的保守性.

由式（6）、（9）、（12），進一步推得系統的閉環動態方程

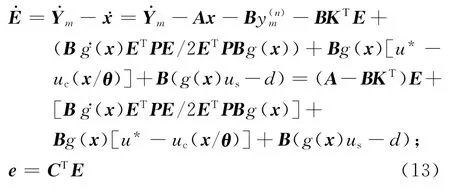
定義誤差w＝（wf－d）／g（x），并假設存在正常數wM，滿足w≤wM.把uc（x／θ）＝θTψ（x）代入式（13）得

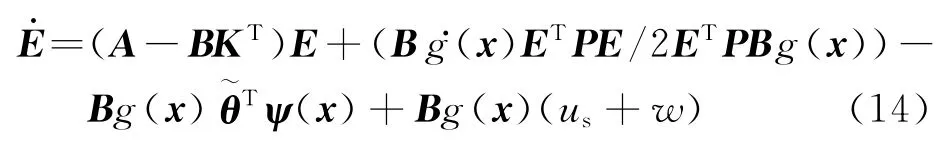
設計魯棒補償控制項us和參數自適應律分別為

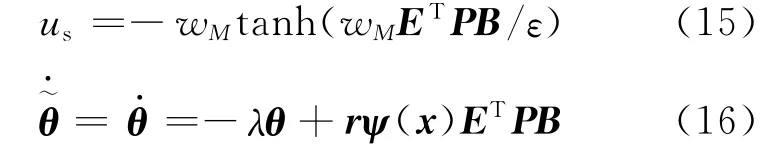
其中λ∈（0，＋∞），r＝diag｛r1，r2，…，rl｝，ri∈（0，＋∞），l是θ的維數，λ、ri、ε是設計者設定的參數.對比文獻［13］，本文的自適應律（16）中不再含有未知函數g（x）或函數的界值，克服了設計中的保守性.下面給出魯棒自適應控制律的有關定理.

定理1 假設形如式（6）的含有不確定項的非線性系統滿足假設1、2，同時滿足式（8），模糊控制器參數θ未知，則設計的模糊控制器式（12）、（15）及自適應律（16）能夠保證系統的所有信號及參數均具有一致有界性；且任意給定ρ＞總存在T（ρ）使得t≥T時，其中rmin＝min｛r1，…，rl｝.

證明 選擇Lyapunov函數如下：

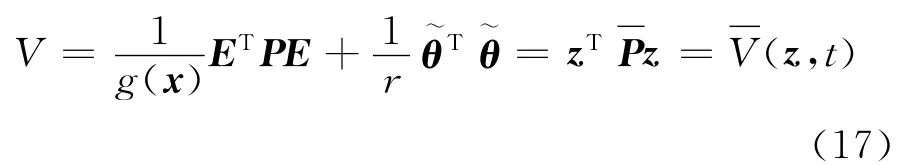
已知對任意的ε＞0和η∈R，存在

其中κ為滿足κ＝exp（－（κ＋1））的常數，即κ＝0.278 5［5］.設η＝wMBTPE，把式（15）代入式（18），并應用式（19）得到

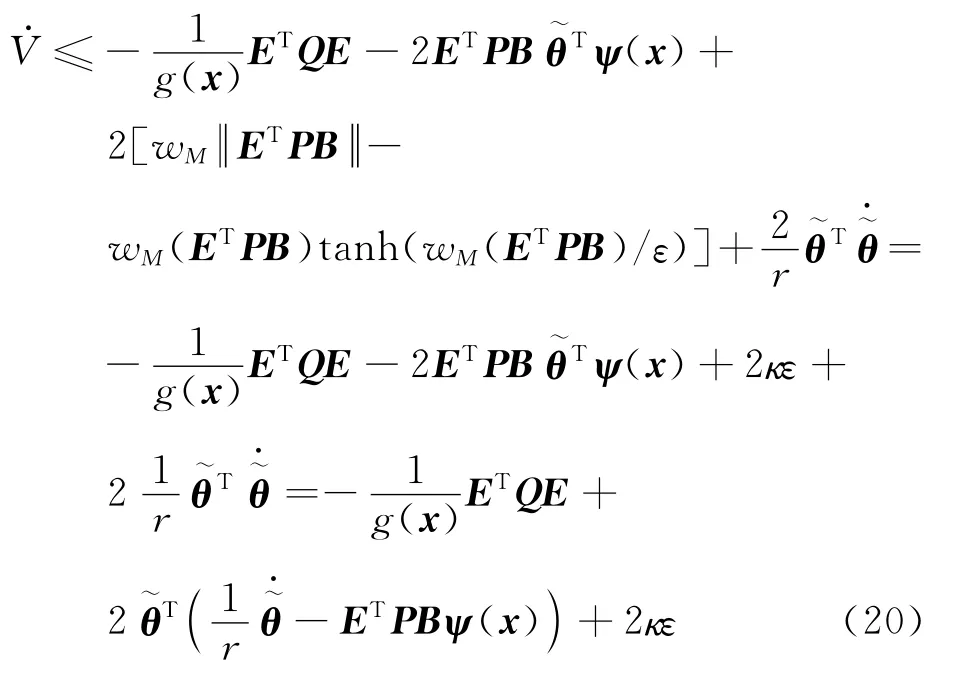
把式（16）代入式（20）得

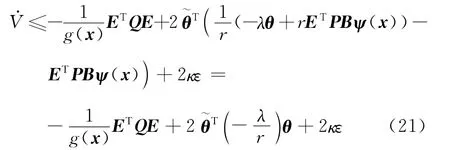
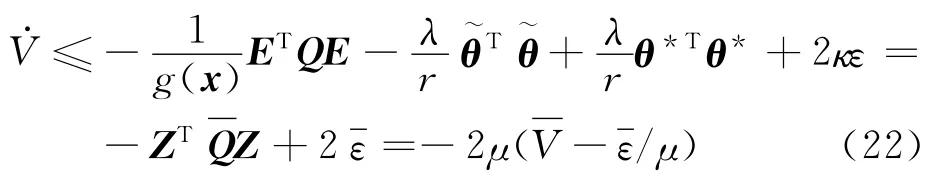
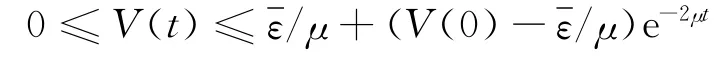
因此，x、θ是一致漸近有界的［18］.進一步，對于任意給定的存在T（ρ）使得t≥T時，滿足證畢.

注釋2 GFHM 是一個全局非線性模型，它由雙曲正切函數的集合組成，模糊控制項uc是連續光滑的變量；另一方面，雙曲正切函數形式的魯棒補償控制項us也是連續光滑的.所以，整個控制輸入是連續光滑控制，無切換抖振現象.

注釋3 當ε取充分小，rmin、λmin（Q）取充分大時，可以使ρ充分小，即閉環跟蹤控制系統的跟蹤誤差充分小.

注釋4 為了確保參數θ∈Ωθ，需要采用投影算法修正參數的自適應律［1］.即如果參數在約束集內部或邊界，且正向約束集內部移動，則使用基本自適應律；如果參數在約束集邊界上，且正向約束集外部移動，則將參數向量的梯度映射到支撐超平面上.應用投影定理修正的自適應律為

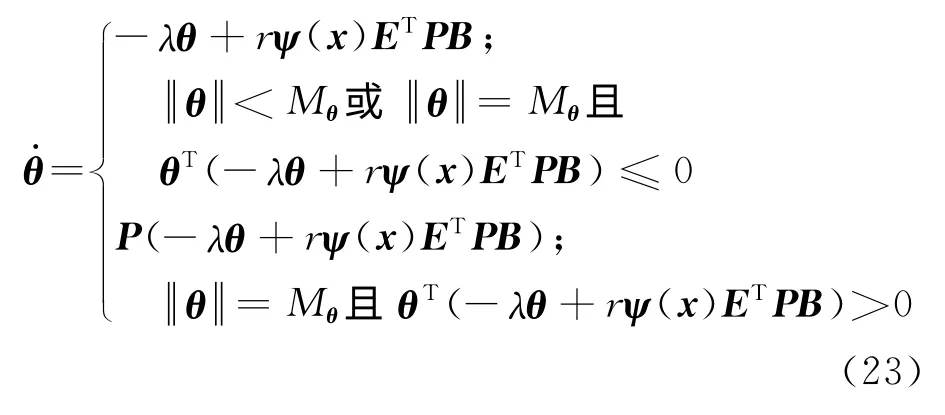
其中投影算子

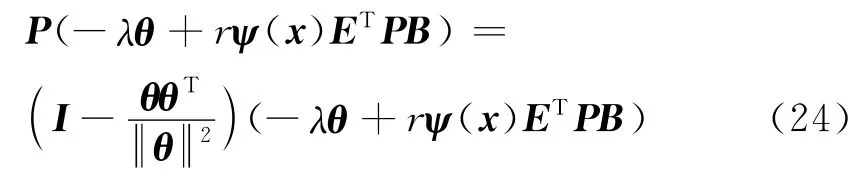
注釋5 在定理1 中，函數g（x）的上界只作分析用途，也即在設計控制器（12）時并不需要用到，從而降低了函數界值估計過大導致的控制器設計的保守性.

4 仿真實例

應用上述魯棒自適應控制算法來控制小車倒立擺跟蹤系統.倒立擺的動態方程［5］：

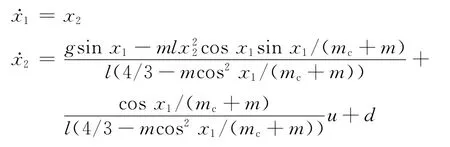
式中：倒立擺的擺角為x1，角加速度為x2.初始條件x（0）＝ （0.2 0）T，跟蹤信號ym（t）＝（π／30）sint，其 他參數同文獻［5］.根據經驗取wM＝3，應用本文提出的控制算法，取λ＝1，（1tanh（0.2x1） tanh（0.4x2））T，外部不確定的干擾d＝0.2sin（20πt）.

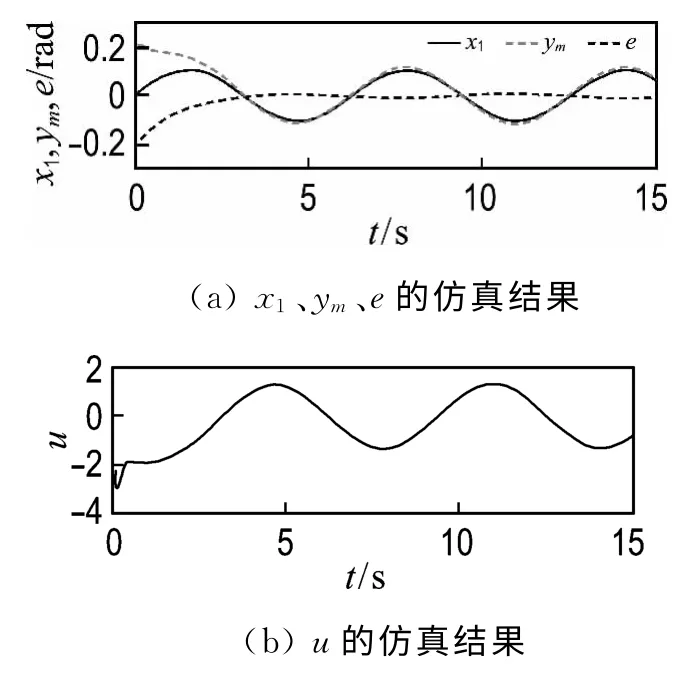
仿真結果如圖1所示.圖中系統跟蹤誤差很快收斂趨于零，并且控制輸入量光滑連續有界，可見，本文的魯棒自適應控制算法實現了系統跟蹤誤差收斂.

5 結 語

本文針對一類含有不確定項的非線性系統，在控制增益函數及其界均未知的條件下，僅要求控制增益函數為有界函數，提出了一種新的魯棒自適應模糊控制算法，從而降低了函數界值估計過大導致的控制器設計的保守性.本文的控制策略能保證控制系統跟蹤誤差收斂至充分小，獲得較好的跟蹤效果，且所有的變量均具有一致有界性.

［1］ WANG Li－xin.Stable adaptive fuzzy control of nonlinear systems［J］.IEEE Transactions on Fuzzy Systems，1993，1（2）：146－155.

［2］ PAN Yong－ping，Er M J，HUANG Dao－ping，etal.Adaptive fuzzy control with guaranteed convergence of optimal approximation error ［J］.IEEE Transactions on Fuzzy Systems，2011，19（5）：807－818.

［3］ PAN Yong－ping，ZHOU Yu，SUN Tai－ren，etal.Composite adaptive fuzzyH∞tracking control of uncertain nonlinear systems［J］.Neurocomputing，2013，99：15－24.

［4］ Lin T C，Wang C H，Liu H L.Observer－based indirect adaptive fuzzy－neural tracking control for nonlinear SISO systems using VSS andH∞approaches［J］.Fuzzy Sets and Systems，2004，143（2）：211－232.

［5］ Park J H，Park G T，Seong S J，etal.Outputfeedback control of uncertain nonlinear systems using a self－structuring adaptive fuzzy observer［J］.Fuzzy Sets and Systems，2005，151（1）：21－42.

［6］ HAN Hu－gang，SU Chun－yi，Stepanenko Y.Adaptive control of a class of nonlinear systems with nonlinearly parameterized fuzzy approximators［J］.IEEE Transactions on Fuzzy Systems，2001，9（2）：315－323.

［7］ SU Chun－yi，Oya M，Hong H.Stable adaptive fuzzy control of nonlinear systems preceded by unknown backlash－like hysteresis ［J］.IEEE Transactions on Fuzzy Systems，2003，11（1）：1－8.

［8］ Chen C S.Quadratic optimal neural fuzzy control for synchronization of uncertain chaotic systems［J］.Expert Systems with Applications，2009，36（9）：11827－11835.

［9］ Lin C M，Hsu C F.Adaptive fuzzy sliding－mode control for induction servomotor systems［J］.IEEE Transactions on Energy Conversion，2004，19（2）：362－368.

［10］ Wai R J，Chang L J.Stabilizing and tracking control of nonlinear dual－axis inverted－pendulum system using fuzzy neural network ［J］.IEEE Transactions on Fuzzy Systems，2006，14（1）：145－168.

［11］ 佟紹成，柴天佑.非線性系統的直接自適應輸出反饋監督模糊控制［J］.控制與決策，2004，19（3）：257－261.TONG Shao－cheng，CHAI Tian－you.Direct adaptive fuzzy output feedback control for uncertain nonlinear systems［J］.Control and Decision，2004，19（3）：257－261.（in Chinese）

［12］ 鄭亞琴，劉艷軍，佟紹成.具有監督控制功能的非線性系統的直接自適應模糊控制［C］／／2009中國控制與決策會議.沈陽：東北大學出版社，2009：918－923.ZHENG Ya－qin，LIU Yan－jun，TONG Shao－cheng.Direct adaptive fuzzy control for nonlinear systems with supervisory control performance［C］／／2009 Chinese Control and Decision Conference.Shanyang：Northeastern University Press，2009：918－923.（in Chinese）

［13］ 張明君，張化光.一種魯棒直接自適應模糊控制算法［J］.東北大學學報：自然科學版，2006，27（1）：5－8.ZHANG Ming－jun，ZHANG Hua－guang.A robust direct adaptive fuzzy control algorithm ［J］.Journal of Northeastern University：Natural Science，2006，27（1）：5－8.（in Chinese）

［14］ ZHANG Hua－guang，QUAN Yong－bing.Modelling，identification and control of a class of non－linear system［J］.IEEE Transactions on Fuzzy Systems，2001，9（2）：349－354.

［15］ 全永兵，張化光.廣義模糊雙曲正切模型及其逼近性研究［J］.東北大學學報：自然科學版，2003，24（1）：1－3.QUAN Yong－bing，ZHANG Hua－guang.Generalized fuzzy hyperbolic model：a universal approximator［J］.Journal of Northeastern University：Natural Science，2003，24（1）：1－3.（in Chinese）

［16］ ZHANG Hua－guang，WANG Zhi－liang，LIU Derong.Chaotifying fuzzy hyperbolic model using adaptive inverse optimal control approach ［J］.International Journal of Bifurcation and Chaos，2004，14（10）：3505－3517.

［17］ Ge S S，Hang C C，Lee T H，etal.Stable Adaptive Neural Network Control［M］.Boston：Kluwer，2001.

［18］ Corless M.Guaranteed rates of exponential convergence for uncertain systems［J］.Journal of Optimization Theory and Applications，1990，64（3）：481－494.