一種NSCT域多聚焦圖像融合新方法

楊 勇， 童 松， 黃淑英， 方志軍， 楊壽淵

（1. 江西財經大學信息管理學院，江西 南昌330032；2. 江西省數字媒體重點實驗室，江西 南昌330032；3. 江西財經大學軟件與通信工程學院，江西 南昌330032）

一種NSCT域多聚焦圖像融合新方法

楊 勇1,2， 童 松1,2， 黃淑英3， 方志軍1,2， 楊壽淵1,2

（1. 江西財經大學信息管理學院，江西 南昌330032；2. 江西省數字媒體重點實驗室，江西 南昌330032；3. 江西財經大學軟件與通信工程學院，江西 南昌330032）

針對多聚焦圖像融合存在的問題，提出一種基于非下采樣Contourlet變換（NSCT）的多聚焦圖像融合新方法。首先，采用NSCT對多聚焦圖像進行分解；然后，對低頻系數采用基于改進拉普拉斯能量和（SML）的視覺特征對比度進行融合，對高頻系數采用基于二維Log-Gabor能量進行融合；最后，對得到的融合系數進行重構得到融合圖像。實驗結果表明，無論是運用視覺的主觀評價，還是基于互信息、邊緣信息保留值等客觀評價標準，該文所提方法都優于傳統的離散小波變換、平移不變離散小波變換、NSCT等融合方法。

多聚焦圖像融合；非下采樣Contourlet變換；Log-Gabor能量；改進拉普拉斯能量和

圖像融合是圖像處理領域的一個重要分支，它的思想是綜合利用不同圖像傳感器或同一傳感器在不同時間或方式得到的多幅圖像合成一幅滿足某種需求或蘊含更多有價值信息的新圖像，使得對目標或場景的描述更加準確、全面。目前，圖像融合技術已被廣泛應用于遙感[1]、醫學診斷[2]、計算機視覺[3]等領域。

在照相機及光學顯微鏡等設備中，由于光學鏡片聚焦范圍有限，要得到場景中所有目標都清晰的成像是很困難的，往往某個場景的成像是一部分聚焦(表現為清晰)，一部分離焦(表現為模糊)[4]。然而，在現實中人們往往希望看到的所有目標圖像都清晰。通過多聚焦圖像融合技術，可以對同一場景下多幅聚焦不同的圖像進行合并得到一幅全景都清晰的圖像[5]。

圖像融合方法通常分為空間域融合方法和變換域融合方法[6]。空間域融合方法是直接在源圖像的像素灰度或色彩空間上進行融合操作，所以其方法也稱為單尺度融合方法；變換域融合方法是先將源圖像經過某種特定的數學變換，然后對變換后的系數按照某種融合規則進行組合，得到融合圖像的變換系數，最后進行數學反變換得到融合圖像。在基于空間域的多聚焦圖像融合算法中，最常用的方法是加權平均法，即對源圖像的各個像素的值進行加權平均處理。該方法對于圖像清晰部分和邊緣部分無法完全或準確地提取，容易造成源圖像中部分有用信息丟失，降低融合結果的對比度[7]，從而使結果的細節部分出現不同程度的模糊。所以這種方法雖然計算簡單，時間復雜度低，但效果卻最差[8]。

基于變換域多聚焦圖像融合算法中比較流行的是使用多尺度變換，包括拉普拉斯金字塔變換(Laplacian pyramid, LP)、梯度金字塔變換(gradient pyramid, GP)、小波變換和其他的多尺度變換[9-15]。由于多尺度變換與人眼視覺多通道分解率的規律一致，可以得到更加接近人眼視覺特性的融合效果[9]。其中，離散小波變換(discrete wavelet transform, DWT)作為圖像融合領域中最為常用的一種多尺度方法因其具有良好的時域和頻域局部分析特性受到廣泛重視[10]。但是小波變換不具有平移不變性，使得融合圖像在奇異處容易產生頻譜混疊效應，導致融合圖像失真。為克服這一問題，有人提出來平移不變離散小波變換(shift-invariant discrete wavelet transform, SIDWT)，并成功用于圖像融合中[11]。但是，由于二維小波基所具有的方向有限，不能最稀疏的表示圖像，只能捕獲到有限的方向信息，導致不能有效地描述圖像的輪廓和方向紋理特征[12]。Do和Vetterli[12]提出的Contourlet變換克服了小波變換的不足。然而，Contourlet變換由于其在分解和重構過程中的上、下采樣導致其同樣不具有平移不變特性，也容易出現頻譜混疊效應[13]。Cunha等[14]在 Contourlet變換的基礎上又提出了非下采樣Contourlet變換(non-subsampled contourlet transform, NSCT)。NSCT不僅繼承了Contourlet變換的優點，而且還不需要上、下采樣達到平移不變的效果，有效地克服了頻譜混疊效應[15]。

在基于多尺度變換的圖像融合過程中，如何在變換域中進行系數融合是決定融合效果的另一重要問題。對于低頻子帶，一般直接采用平均法，但是這種方法容易使源圖像的部分有用信息丟失，在一定程度上降低了圖像的對比度；對于高頻子帶，一般認為絕對值越大的高頻系數，擁有越明顯的細節信息，由文獻[16]可知，這種方式由于忽略了系數之間的相關性，可能得出錯誤的系數映射方式。

為克服這個缺陷，結合局部能量的思想，本文提出了一種基于NSCT的多聚焦圖像融合新方法。該方法首先對源圖像進行NSCT分解；然后對低頻系數采用基于改進拉普拉斯能量和(sum-modified-Laplacian, SML)的視覺特征對比度進行融合，對高頻系數采用基于二維Log-Gabor能量進行融合；最后，對得到的融合系數進行重構得到融合圖像。實驗結果表明，融合圖像無論從主觀和客觀評價上都能得到很好地效果。

1 非下采樣Contourlet變換

Contourlet變換是由 LP和方向濾波器組(directional filter bank, DFB)兩部分結合實現[12]。其中，LP用來捕獲圖像中的奇異點，DFB用來將捕獲的奇異點連接成線性的結構。從濾波器的角度看，LP濾波器是將原圖像分解成低頻和高頻子帶，DFB將獲得的高頻子帶分解為各方向的子帶。Contourlet分解示意圖如圖 1所示。在 Contourlet變換過程中，LP的分解和重構濾波器組為二維可分離的正交濾波器組，帶寬均大于 。由多采樣理論可知，在低頻子帶和高頻子帶均會出現頻譜混疊效應。由于方向子帶是由高頻子帶通過 DFB獲得，所以方向子帶也存在頻譜混疊效應。從而在一定程度上削弱了該方法的方向選擇性。

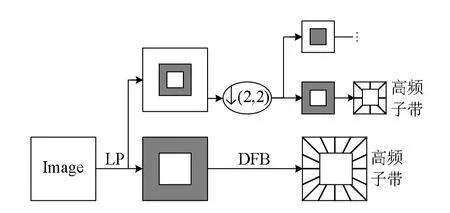
圖1 Contourlet分解示意圖

為解決這一問題，Cunha等[14]提出了NSCT。NSCT變換是在Contourlet變換的基礎上提出來的，它不僅繼承了Contourlet變換多方向、多尺度、各向異性等特性，還增強了它的方向選擇性和平移不變性，有效克服了頻譜混疊效應[17]。NSCT變換分為兩個部分：非采樣金字塔濾波器 (non-subsampled pyramid filter bank, NSPFB)和非采樣方向濾波器(non-subsampled directional filter bank, NSDFB)。圖2為NSCT兩層分解的框架。NSPFB是一個雙通道非下采樣濾波器組，它的結構類似于 LP，但是通過對濾波器采取差值（上采樣）操作來回除下采樣過程。NSDFB的結構與NSPFB相似，它是由一個具有扇形濾波器的非下采樣濾波器組構成。二通道濾波器組的設計是 NSCT算法構造的核心，由于NSPFB和 NSDFB都滿足 Bezout恒等式，因此NSCT可以完全重建。因為NSPFB和NSDFB在分解和重構的過程中沒有下采樣和上采樣，所以NSCT具有平移不變性，并且分解后的低頻子帶也不會產生頻譜混疊效應。

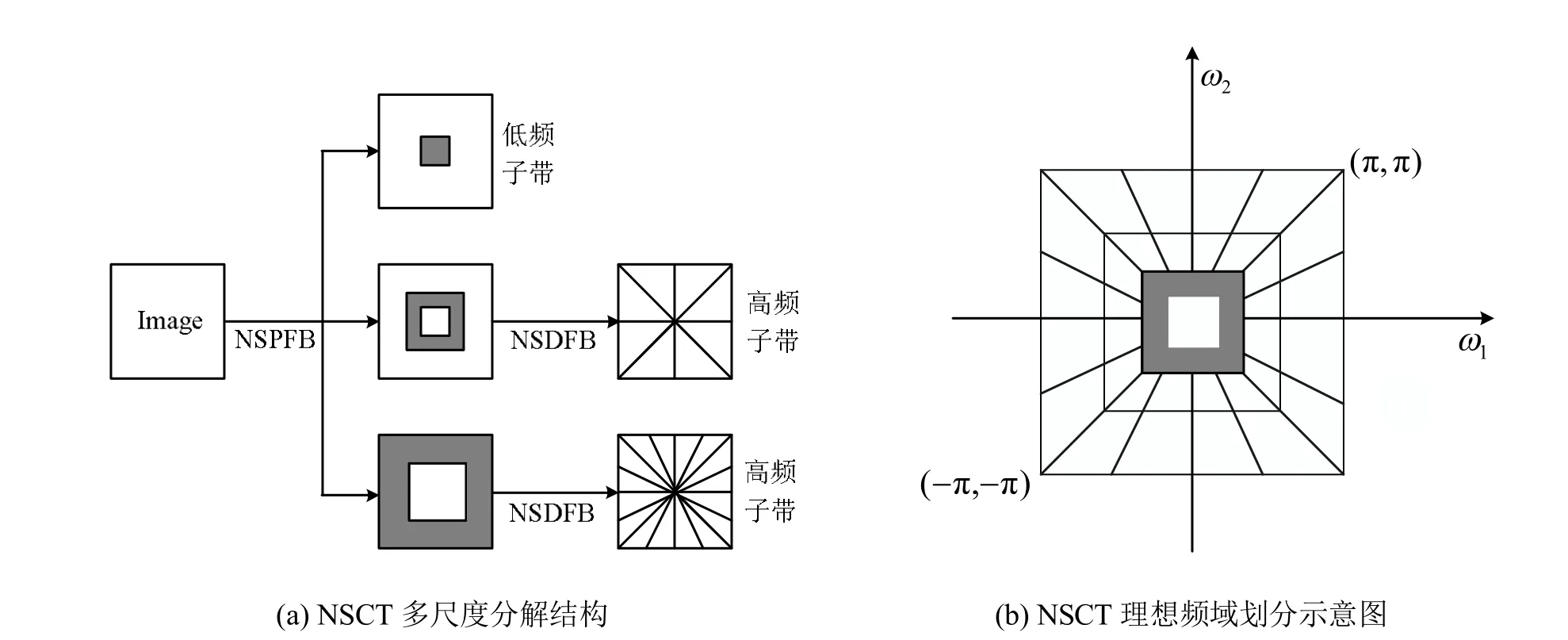
圖2 NSCT二級分解

2 本文提出的融合方法

上一節介紹的 NSCT變換，不僅繼承了Contourlet變換的優良特性，還具有良好的方向選擇性和平移不變性，是一種超完備的多尺度變換，融合性能優越[15]。因此，本文選用 NSCT分解和重構來獲得融合圖像。在 NSCT變換的過程中，如何在變換域中進行系數融合是一個至關重要的問題[17]。為得到一個紋理清楚、視覺效果良好的融合圖像，本文分別構建了基于SML的局部視覺特性對比度和二維 Log-Gabor能量的低頻和高頻融合規則。

2.1 低頻子帶的融合規則

圖像經NSCT變換的低頻系數，代表了源圖像的近似信息，反映了源圖像的灰度信息，包含了源圖像大部分能量。文獻[18]指出，在空間域中，圖像梯度能量(energy of image gradient, EOG)、空間頻率(spatial frequency, SF)、拉普拉斯能量(energy of Laplacian, EOL)、SML等清晰度評價指標的融合性能中，SML最適合局部聚焦程度的評價。

由文獻[19]可知，人眼視覺特性在對比度敏感門限與背景亮度上具有非線性關系。綜合考慮人眼視覺特性及 SML的優良特性，本文提出對低頻子帶系數采用基于 SML的視覺特性對比度的融合規則。以源圖像A的低頻子帶為例，基于SML的視覺特性對比度LV的定義如下：

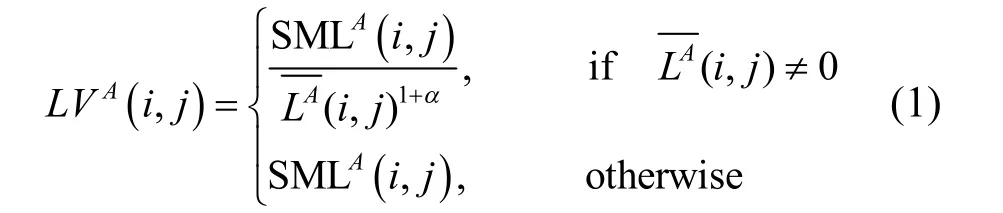
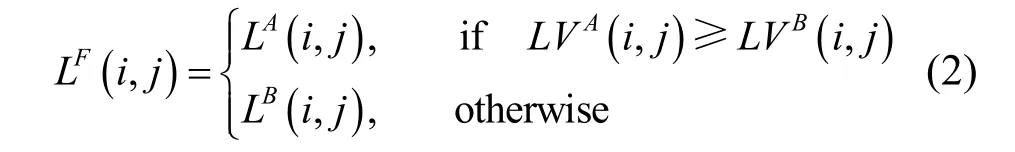
2.2高頻子帶的融合規則

圖像經NSCT變換的高頻子帶主要包括圖像的紋理和邊緣等細節信息。一般認為絕對值越大的高頻系數，擁有越明顯的細節信息，由文獻[16]可知，這種方式由于忽略了系數之間的相關性，可能得出錯誤的系數映射方式。為克服這個缺陷，受文獻[20]的啟發，并結合局部能量的思想，本文設計了一種以局部Log-Gabor能量的大小作為高頻融合規則的新方法。

Gabor濾波器是一種重要的紋理特征提取方法，這種方法借鑒心理生理學的研究成果，模擬方向可選神經元的計算機制，通過將Gabor函數作為小波變換的基函數，來實現尺度不變的特征提取[21]。Log-Gabor濾波器是以Gabor濾波器為基礎提出的，與Gabor濾波器相比，其傳遞函數的設計彌補了Gabor 濾波器對高頻分量表達的不足，更符合人眼視覺感知特性，可以在取得最佳空間定位的同時得到盡可能寬的頻譜信息，更真實地反映自然圖像的頻率響應[22]。

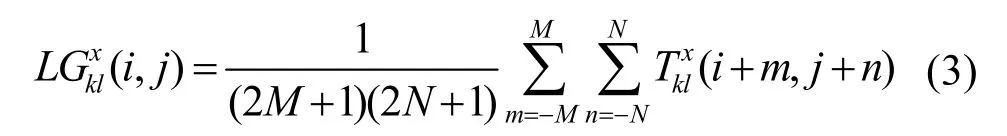
其中，(2 M + 1)(2 N+ 1)為窗口大小， T（i, j ）代表了圖像x在k尺度l方向上的高頻子帶的Log-Gabor能量的大小。

由于多聚焦圖像通常在聚焦區域擁有豐富的高頻信息，非聚焦區域的高頻信息相對匱乏，通過比較圖像各個高頻子帶系數的局部Log-Gabor能量大小分析高頻子帶的聚焦程度，是可行的。為此，本文選擇的高頻融合方案為：

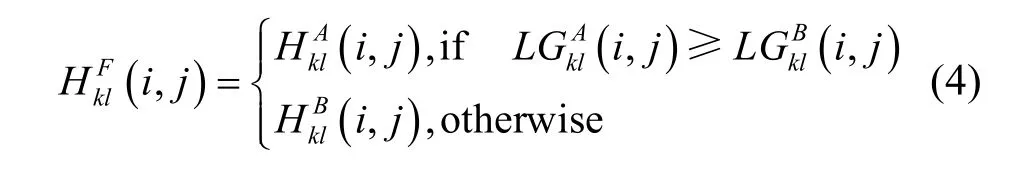
2.3 圖像融合總體框架

設計出低頻和高頻系數融合規則后，基于多尺度變換融合的一般方法，本文提出如圖3所示的基于NSCT的圖像融合框架。具體融合步驟如下：

步驟 1.對預處理后的源圖像 A、B分別進行NSCT分解，圖像大小設為 M0N0。其中定義NSCT的尺度分解為k級，每一級尺度下的方向分解數定義為l個。源圖像A、B分解后得到的NSCT分解系數分別為：｝和，其中L為低頻子帶系數， Hk,l為k尺度下第l個方向的高頻子帶系數。本文中取尺度分解級數 k=3，方向分解數

步驟2.通過上述2.1和2.2節提出的融合規則分別對分解后的低頻子帶和高頻子帶進行系數融合。

步驟3.采用NSCT逆變換對步驟2中得到的低頻子帶融合系數和高頻子帶融合系數 LF（i, j）和H（i,j）進行重構，即可得到融合圖像F。

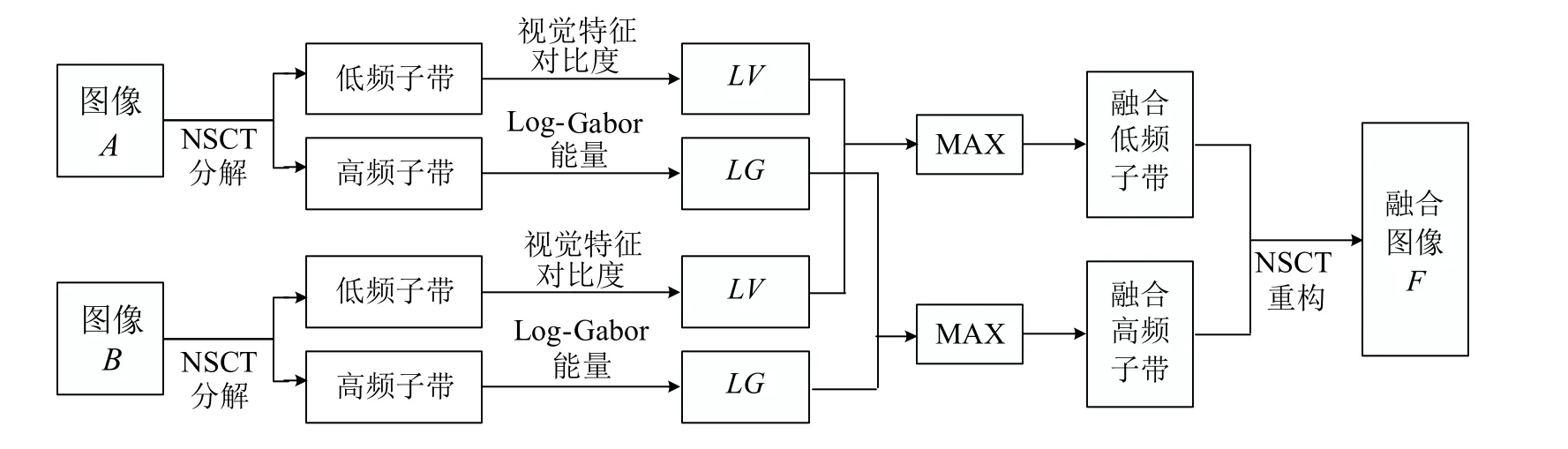
圖3 基于NSCT的圖像融合框架

3 實驗結果及分析

為驗證本文提出融合算法的準確性和魯棒性，論文選取了四組多聚焦圖像進行融合實驗。實驗數據如圖4所示，圖中每兩幅為一組待融合圖像，依次標記為圖像組Cameraman、Pepsi、Clock、Lab。前三組圖像大小均為256×256，圖像組Lab的大小均為640×480。

為更好地評估本文的融合算法性能，對每一組實驗分別采用另外5種融合算法與本文算法進行對比實驗。在5種融合算法中：第一種方法為加權平均法，權值分別是0.5；后4種算法分別采用基于GP的融合算法、基于 DWT的融合算法、基于SIDWT的融合方法和基于NSCT的融合算法，均采用常用的高頻取絕對值最大、低頻取平均的融合規則，其中DWT為三層分解，基為DBSS(2, 2)；SIDWT也為三層分解，基為Haar；NSCT的分解層數及各層方向數是[1, 2, 8]，金字塔濾波器組為‘9-7’方向濾波器組為‘pkva’。

實驗中，除了從視覺效果上評價融合結果外，本文還引入了互信息(mutual information, MI)和邊緣保持度(QAB/F)兩個客觀評價指標來評價本文提出的融合算法的性能。

MI是融合圖像F與源圖像A與B的互信息量，可以用來對融合圖像F包含源圖像A和B的信息量進行度量[23]，其值越大即說明源圖像有越多信息轉移到了融合結果中，則融合效果更好。定義如下：

其中

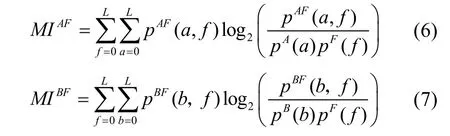
表示融合圖像F分別與源圖像A、B的互信息量。pA(a)、pB(b)、pF(f)分別表示源圖像 A、B和融合圖像F的概率密度函數，由對應圖像的灰度直方圖估計得到。pAF(a,f)、pBF(b，f)分別表示源圖像A或B與融合圖像F的聯合密度函數，由對應兩幅圖像的歸一化聯合灰度直方圖估計得到。

QAB/F評價算子是由Xydeas和 Petrovi?[24]提出的，該算子通過sobel邊緣檢測算子來衡量源圖像邊緣信息轉移到融合圖像的多少，它的值越大，說明轉移的邊緣信息越多，則融合效果越好。其定義如下：

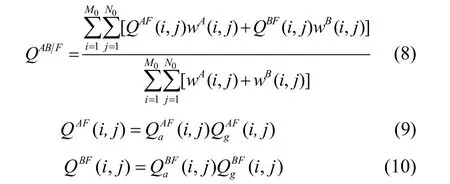
其中，M0與 N0表示圖像的尺寸和分別表示源圖像 A和 B的邊緣強度。 Q(i,j)和Q(i,j)分別表示融合圖像F相對源圖像x的邊緣強度和方向的保留度。

圖4 實驗數據(a)、(b)為圖像組Cameraman；(c)、(d)為圖像組Pepsi；(e)、(f)為圖像組Clock；(g)、(h)為圖像組Lab

第一組實驗，本文選用了人工多聚焦圖像組Cameraman (圖4(a)～(b))進行了融合實驗。圖5(a)～(f)是不同算法所獲得的融合結果。在圖5中，加權平均法得到的融合結果較為模糊，對比度最差；DWT方法得到的融合結果中有偽影存在（如人物的頭發區域）；其他幾種方法從視覺上很難區分融合結果的優劣。為更好地評估融合結果的差異，本文給出了融合結果與源圖像（圖4(a)）的殘差圖，并對殘差圖做了亮度與梯度的銳化，如圖6所示。本組實驗圖像組是一個上下聚焦的圖像，故本文試圖將圖6中的殘差圖像分為上、下兩部分來分析各融合算法的性能差異。從各殘差圖的下半部分即源圖像（圖4(a)）的聚焦區域可以看出，其中圖6(f)效果最好，下半部分幾乎都是黑色，即本文提出的方法幾乎保留了源圖像中聚焦區域所有的像素點；相反，圖6(a)的效果最差，對源圖像的聚焦區域的信息損失最大。圖6(b)與圖6(c)相比，圖6(b)的信息量更大，即丟失的有用信息也更多，圖6(c)對于聚焦區域的信息獲取較多，效果相對較好。圖6(c)與圖6(e)相比，圖6(e)對源圖像有用信息的捕獲能力要明顯好于圖6(c)。圖6(d)與圖6(e)相比，圖6(d)在目標人物的衣服邊界以及相機三腳架的邊界信息丟失要比圖6(e)明顯。從每幅圖像的上半部分（即圖5(a)的離焦區域）可以看出，圖6(c)～(f)都可以看到目標人物以及背景建筑清晰的局部特征，圖6(a)與圖6(b)相對模糊；圖6(c)相對于圖6(d)～(f)，邊緣出現明顯的偽影，邊緣和紋理表現較弱。

綜合圖5和圖6的結果可以看出：加權平均法得到的融合圖像視覺效果最差；基于DWT的方法對于聚焦區域的信息提取方面要明顯優于梯度金字塔變換，這是因為金字塔分解和重構的過程中丟失了較多高頻信息，導致細節特征不明顯。而在圖像的邊緣部分NSCT變換要優于DWT和SIDWT變換，這是因為NSCT使用了更好地分解和重構工具，對于圖像線奇異的捕獲能力更強。本文提出的融合算法也明顯優于傳統的基于NSCT得到的融合結果，這也說明本文融合規則的有效性。因此，從本組實驗對比可以得出，本文提出的融合方法融合效果要優于其他5種算法，有效地保留了源圖像中清晰部分的信息，最大限度地保留了源圖像的有用信息。

圖5 不同方法所獲得的圖像組Cameraman的融合結果

圖6 不同方法所獲得的圖像組Cameraman的融合結果與源圖像（圖4(a)）之間的殘差圖

為說明本文提出的融合算法可以廣泛地適用于多聚焦圖像融合，本文還給出了3組融合實驗。融合圖像分別為多聚焦圖像組Pepsi、Clock和存在配準誤差的圖像組Lab(如圖4(c)～(h))。圖7和圖9為不同方法所獲得的圖像組 Pepsi和圖像組 Clock的融合結果，其中兩組圖像里的(a)、(b)比其他四幅圖像相對模糊，即前兩種方法相對于其他方法要差。圖8和圖10為不同方法所獲得的圖像組Pepsi和圖像組Clock的殘差圖。通過圖8和圖10可以看出，基于NSCT的融合方法相比于基于DWT的融合方法在融合圖像中保留了源圖像聚焦區域更多的細節信息，這是因為NSCT多方向性克服了傳統小波變換方向有限的缺點，保留了源圖像更多的有用信息。圖8(f)和圖10(f)在源圖像的聚焦區域幾乎表現為黑色，這也就說，本文提出的方法幾乎保留了源圖像聚焦區域中的全部有用信息，所提出的方法捕獲源圖像中聚焦部分和細節部分信息的能力要大大優于另外5種方法。

圖11表示不同方法所獲得的圖像組Lab的融合結果。從源圖 4(g)～(h)可以看出，這兩幅圖像的學生頭像之間存在輕微的位置差異，這說明圖像組Lab中的兩幅圖存在少許的配準誤差。從實驗結果圖 11看出，即使存在配準誤差的情況下，本文提出的融合算法也能得到視覺效果良好的融合結果（如矩形框內所示），說明本文融合方法對配準具有很好的魯棒性。

圖7 不同方法所獲得的圖像組Pepsi的融合結果

圖8 不同方法所獲得的圖像組Pepsi的融合結果與源圖像(圖4(c))之間的殘差圖

圖9 不同方法所獲得的圖像組Pepsi的融合結果

圖10 不同方法所獲得的圖像組Clock的融合結果與源圖像（圖4(e)）之間的殘差圖

圖11 不同方法所獲得的圖像組Lab的融合結果

最后，為了更為客觀地評價上述6種融合算法的性能，利用MI和QAB/F進行了定量評價，評價結果如表1所示。從表1的數據分析可以看出，加權平均法所得到融合圖像的 QAB/F最低，而梯度金字塔由于其是一種冗余變換，在變換過程中丟失過多的有用信息，所以在互信息這個指標上要明顯低于其他變換；DWT是一種非冗余變換，在源圖像有用信息的保留和細節的保持度上都高于梯度金字塔變換方法得到的融合結果；SIDWT通過非下采樣變換克服了頻譜混疊效應，所得到的定量評價要明顯好于DWT；NSCT通過其多方向性保留了源圖像更多方向上的細節信息，使得MI和QAB/F兩個方面相對要優于 SIDWT；本文提出的算法也要明顯優于傳統NSCT變換，在兩個評價指標上都獲得明顯地提高，這也說明了本文提出的基于 SML的視覺特征對比度和基于局部Log-Gabor能量的融合規則的有效性。綜上所述，無論是主觀視覺還是客觀指標，本文算法融合效果都要優于其他5種方法。

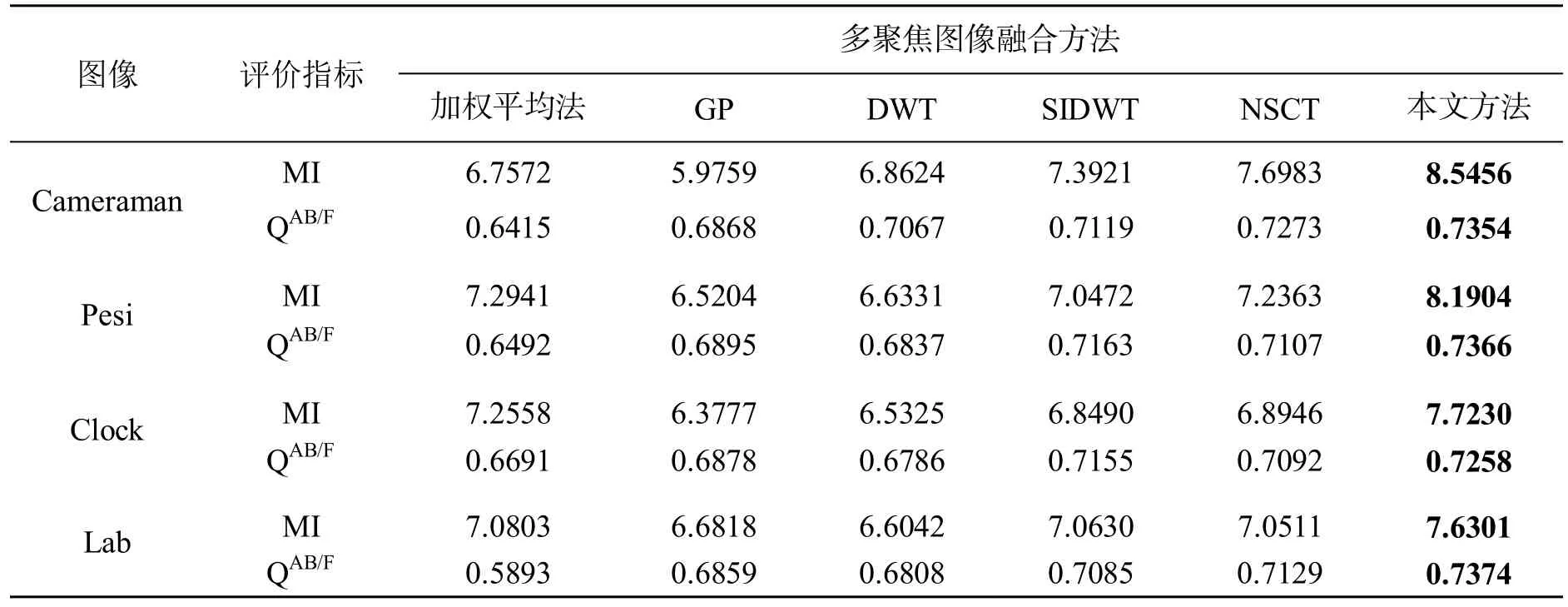
表1 不同多聚焦圖像融合方法得的客觀指標對比

4 結 束 語

針對多聚焦圖像融合存在的主要問題，提出一種基于NSCT的多聚焦圖像融合新方法。首先，構建了源圖像經NSCT分解后的融合規則選取方案，提出了基于 SML的視覺特征對比度的低頻融合規則和基于Log-Gabor能量的高頻融合規則。最后，在此基礎上給出了一個新的NSCT域多聚焦圖像融合框架。大量的實驗結果對比和分析都充分證明了本文所提出的融合方法的有效性。由于NSCT算法自身的復雜度高、計算耗時長，因此下一步將研究提高算法的運算速度。

[1] Zhang Zhou, Shi Zhenwei, An Zhenyu. Hyperspectral and panchromatic image fusion using unmixing-based constrained nonnegative matrix factorization [J]. Optik-International Journal for Light and Electron Optics, 2013, 124(13): 1601-1608.

[2] Miles B, Ben A I, Law M W K, Garvin G, Fenster A, Li Shuo. Spine image fusion via graph cuts [J]. IEEE Transactions on Biomedical Engineering, 2013, 60(7): 1841-1850.

[3] Liang Junli, He Yang, Liu Ding, Zeng Xianju. Image fusion using higher order singular value decomposition [J]. IEEE Transactions on Image Processing, 2012, 21(5): 2898-2909.

[4] Yang Yong, Zheng Wenjuan, Huang Shuying. A novel automatic block-based multi-focus image fusion via genetic algorithm [J]. KSII Transactions on Internet and Information Systems, 2013, 7(7): 1671-1689.

[5] Yang Bing, Li Shutao. Multifocus image fusion and restoration with sparse representation [J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 884-892.

[6] Liu Yipeng, Jin Jing, Wang Qiang, Shen Yi, Dong Xiaoqiu. Region level based multi-focus image fusion using quaternion wavelet and normalized cut [J]. Signal Processing, 2014, 97(4): 9-30.

[7] Zhang Zhong, Blum R S. A categorization of multiscale-decomposition-based image fusion schemeswith a performance study for a digital camera application [J]. Proceeding of the IEEE, 1999, 87(8): 1315-1326.

[8] 李樹濤, 王耀南, 張昌凡. 基于視覺特性的多聚焦圖像融合[J]. 電子學報, 2001, 29(12): 1699-1701.

[9] 王 麗, 盧 迪, 呂劍飛. 一種基于小波方向對比度的多聚焦圖像融合方法[J]. 中國圖象圖形學報, 2008, 13(1): 145-150.

[10] Chipman L J, Orr T M, Graham L N. Wavelets and image fusion [C]//International Symposium on Optical Science, Engineering, and Instrumentation. International Society for Optics and Photonics, 1995: 248-251.

[11] Ioannidou S, Karathanassi V. Investigation of the dual-tree complex and shift-invariant discrete wavelet transforms on Quickbird image fusion [J]. Geoscience and Remote Sensing Letters, IEEE, 2007, 4(1): 166-170.

[12] Do M N, Vetterli M. The contourlet transform: an efficient directional multiresolution image representation [J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106.

[13] 屈小波, 閆敬文, 楊貴德. 改進拉普拉斯能量和的尖銳頻率局部化 Contourlet域多聚焦圖像融合方法[J]. 光學精密工程, 2009, 17(5): 1203-1212.

[14] Cunha A L, Zhou Jianping, Do M N. The nonsubsampled Contourlet transform: theory, design and applications [J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089-3101.

[15] Bhatnagar G, Jonathan Wu Q M, Liu Zheng. Directive contrast based multimodal medical image fusion in NSCT domain [J]. IEEE Transactions on Multimedia, 2013, 15(5): 1014-1024.

[16] 李華鋒, 柴 毅, 張曉陽. 基于多尺度積視覺特性的多聚焦圖像融合算法[J]. 控制與決策, 2012, 27(3): 355-361.

[17] Qu Xiaobo, Yan Jingwen, Xiao Hongzhi, Zhu Ziqian. Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain [J]. Acta Automatican Sinica, 2008, 34(12): 1508-1514.

[18] Huang Wei, Jing Zhongliang. Evaluation of focus measures in multi-focus image fusion [J]. Pattern Recognition Letters, 2007, 28(4): 493-500.

[19] Bhatnagar G, Jonathan Wu Q M, Liu Zheng. Human visual system inspired multi-modal medical image fusion framework [J]. Expert Systems with Applications, 2013, 40(5): 1708-1720.

[20] Redondo R, ?roubek F, Fischer S, Cristobal G. Multifocus image fusion using the Log-Gabor transform and a multisize windows technique [J]. Information Fusion, 2009, 10(2): 163-171.

[21] Yao Peng, Li Jun, Ye Xueyi, Zhuang Zhenquan, Li Bin. Iris recognition algorithm using modified Log-Gabor filters [C]//18th International Conference on Pattern Recognition, IEEE, 2006: 461-464.

[22] Li Shutao, Yang Bing. Multifocus image fusion using region segmentation and spatial frequency [J]. Image and Vision Computing, 2008, 26(7): 971-979.

[23] Qu Guihong, Zhang Dali, Yan Pingfan. Information measure for performance of image fusion [J]. Electronics Letters, 2002, 38(7): 313-315.

[24] Xydeas C S, Petrovi? V. Objective image fusion performance measures [J]. Electronics Letters, 2000, 36(4): 308-309.

A Novel NSCT-Based Technique for Multi-Focus Image Fusion

Yang Yong1,2, Tong Song1,2, Huang Shuying3, Fang Zhijun1,2, Yang Shouyuan1,2
(1. School of Information Technology, Jiangxi University of Finance and Economics, Nanchang Jiangxi 330032, China; 2. Jiangxi Key Laboratory of Digital Media, Nanchang Jiangxi 330032, China; 3. School of Software and Communication Engineering, Jiangxi University of Finance and Economics, Nanchang Jiangxi 330032, China)

In order to overcome the shortcoming of the traditional multi-focus image fusion methods, a novel non-subsampled contourlet transform (NSCT) based technique for multi-focus image fusion is proposed. Firstly, the source multi-focus images are decomposed by using the NSCT. Secondly, the low-frequency subband coefficients are fused by the local visual contrast mechanism based Sum-Modified-Laplacian (SML), and the high-frequency subband coefficients are fused by a 2D Log-Gabor energy rule. Finally, the inverse NSCT is employed to reconstruct the fused image. Experimental results demonstrate that the proposed method is better than series of popularly used fusion methods, including discrete wavelet transform, shift invariant DWT, NSCT, etc, in terms of both subjective and objective evaluations.

multi-focus image fusion; non-subsampled Contourlet transform; Log-Gabor energy; sum-modified-Laplacian

A

2095-302X(2014)06-0854-10

2014-07-02；定稿日期：2014-08-05

國家自然科學基金資助項目(61262034)；教育部科學技術研究重點資助項目(211087)；江西省自然科學基金資助項目(20114BAB21102, 20132BAB201025)；江西省教育廳科技資助項目(GJJ14334, GJJ09022)；江西省高校科技落地計劃資助項目(KJLD14031)

楊 勇(1976-)，男，湖北鄂州人，教授，博士。主要研究方向為圖像處理、醫學圖像處理與分析、模式識別。E-mail：greatyangy@126.com

TP 391.41