含萬向鉸偏斜軸系的超諧波共振及其穩定性分析

朱擁勇，王德石，代仁文

(海軍工程大學兵器工程系，湖北武漢 430033）

含萬向鉸偏斜軸系的超諧波共振及其穩定性分析

朱擁勇，王德石，代仁文

(海軍工程大學兵器工程系，湖北武漢 430033）

研究固有結構偏斜與實際誤差偏斜共同作用下含萬向鉸偏斜軸系的非線性扭轉振動問題。首先推導出偏斜轉子系統的弱非線性扭轉振動方程，然后利用多尺度法求得其在超諧波共振情形下的周期解，并給出穩態周期解的幅頻特性關系式。運用李雅普諾夫第一近似穩定性理論，對系統平衡點進行穩定性研究，得到超諧波共振解振幅隨調諧參數變化的穩定區與不穩定區。最后對不同初始條件下非線性扭轉振動的超諧波共振進行仿真計算。研究結果揭示了含萬向鉸偏斜轉子系統非線性動力學的基本特性，也為進一步分析偏斜轉子系統的分岔與奇異性奠定了基礎。

扭轉振動;超諧波共振;穩定性;偏斜軸系;萬向鉸

0 引言

萬向鉸被普遍應用于各類傳動系統。在該轉子系統中，由萬向鉸引起的角速度波動會導致系統的非線性振動及其運動穩定性問題，同時，在由制造、安裝而產生的實際誤差偏斜作用下，這種振動形式表現出更復雜的特性。在萬向鉸偏斜轉子系統非線性扭轉振動方面，目前研究大都只考慮固有結構偏斜φ，且認為這種固有結構偏斜較小，即將φ當作微量。Porter首先提出了萬向鉸偏斜轉子系統的單自由度非線性扭轉振動模型［1］，這一弱非線性模型成為研究萬向鉸偏斜轉子系統扭轉振動的經典模型并為后續研究者加以推廣。文獻［2］利用KBM方法直接對上述非線性模型進行研究，分析過程較為復雜。文獻［3］將該模型線性化為參數激勵系統，研究簡化系統的穩定圖、幅頻特性曲線及相平面圖，證明了多解共存及突變現象，并指出主參數共振和2階參數共振的鞍點和焦點，整個研究較為全面，但經簡化后并不能完全反映原偏斜轉子系統的振動性態。針對多節萬向傳動軸的扭轉振動也有學者進行了研究［4］，其分析側重點在于研究系統參數對動力放大因素的影響，通過數值計算優化系統參數，達到降低扭轉強度和避免共振的目的。本文主要研究固有結構偏斜與實際誤差偏斜共同作用下萬向鉸轉子系統的非線性扭轉振動問題，利用多尺度法求解非線性模型，得出系統超諧波共振情形下的幅頻特性曲線與相頻特性，并對系統穩態周期運動進行穩定性分析，從而全面反映出萬向鉸偏斜轉子系統的扭轉振動特性。

1 含萬向鉸偏斜軸系的扭振模型

工程實際中，含萬向鉸的轉子系統一般存在2類偏斜:一類是由萬向鉸結構引起的固有偏斜，這種偏斜模型可用驅動軸與從動軸之間的夾角φ表示;另一類為實際誤差偏斜，由于受到軸承安裝誤差等因素影響，驅動軸與實際從動軸之間出現偏斜情形，這種偏斜模型可以用理想從動軸與實際從動軸之間的2個歐拉角α和β表示，也可稱偏斜角，如圖1所示。

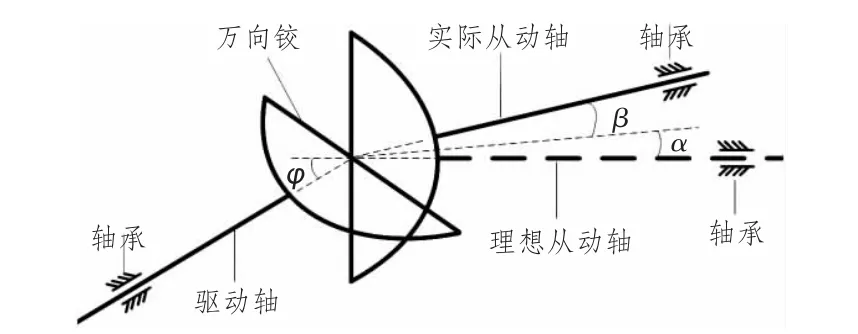
圖1 萬向鉸驅動的偏斜旋轉軸Fig.1 Themodel ofmisaligned rotary shafts driven by universal joint

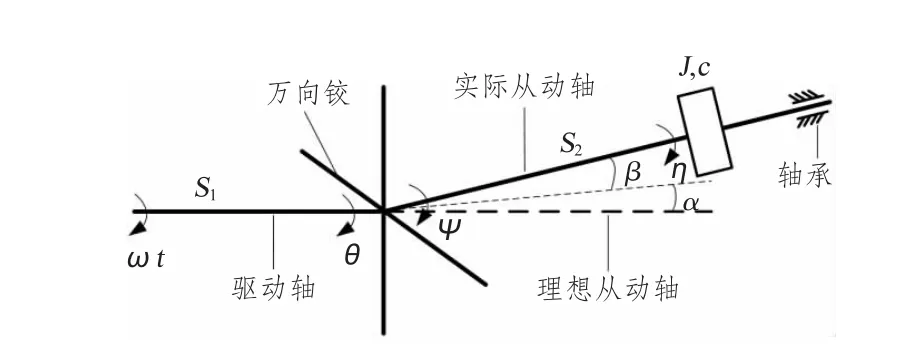
圖2 偏斜轉子系統扭轉振動模型Fig.2 The torsional vibration model on misaligned rotary shafts

為建立偏斜軸系扭轉振動模型，假設:1）驅動軸與從動軸為無質量桿件;2）支承驅動軸與從動軸的軸承足夠長，系統彎曲可以忽略;3）不考慮萬向鉸十字軸的質量，且十字軸與軸叉之間無摩擦。

如圖2所示，在該扭轉振動模型中，驅動軸和從動軸的扭轉剛度分別為S1和S2;驅動軸轉動角速度ω為定值;萬向鉸兩端的輸入角及輸出角分別為θ和ψ，即驅動軸轉角和從動軸轉角;實際從動軸上負載的轉動慣量為J;粘滯阻尼為c(c＞0）;負載端的轉角為η。

一般地，由實際誤差產生的偏斜較小，即偏斜角α和β很小，當萬向鉸固有結構偏斜φ較小時，可以得到驅動軸與從動軸轉動角速度之間的近似關系［5］:

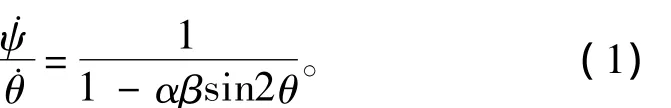
作用在慣性負載上的力矩包括從動軸對負載產生的扭矩以及負載受到的粘滯阻尼扭矩，慣性負載的動力學方程為:

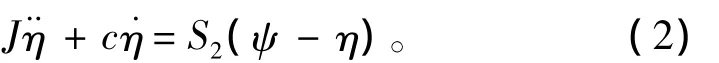
考慮萬向鉸兩端受力情況，萬向鉸輸入端所受力矩為S1(ωt-θ），輸出端產生的力矩為S2(ψη），在假設萬向鉸傳動過程中無摩擦前提下，驅動軸對萬向鉸所做功在某一時刻t的瞬時功率應恒等于十字軸對從動軸所做功在該時刻的瞬時功率，即:

2 超諧波共振情形下的周期解

3 偏斜軸系超諧波共振的穩定性

由式(8）和式(9）得到非線性振動系統超諧波共振情形下的幅頻特性方程:

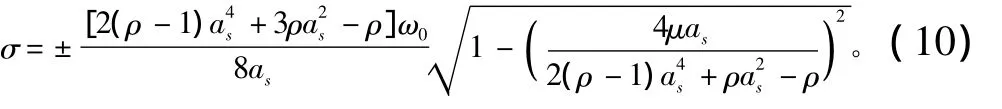
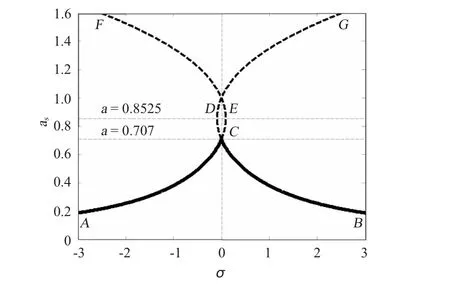
圖3 幅頻特性曲線上的穩定區與不穩定區(ρ =0.5，μ/ρ=0.04）Fig.3 The stability and instability domain on amplitude-frequency curve(ρ=0.5，μ/ρ=0.04）

在圖3所示的幅頻特性曲線中，粗實線ACB為系統周期解的穩定區，其穩定周期解的振幅均小于0.707。虛線a=0.707以上虛線部分為周期解的不穩定區。

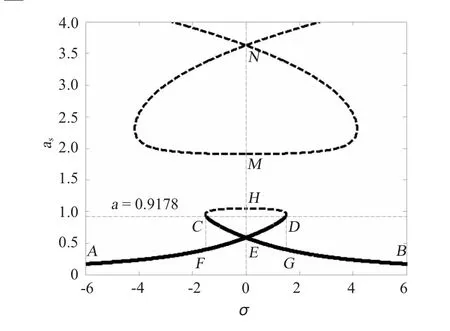
圖4 幅頻特性曲線上的穩定區與不穩定區(ρ =0.9，μ/ρ=0.04）Fig.4 The stability and instability domain on amplitude-frequency curve(ρ=0.9，μ/ρ=0.04）

在圖4所示的幅頻特性曲線中，粗實線AED和BEC為系統周期解的穩定振幅區，其穩定周期解的振幅均小于0.917 8。虛線a=0.917 8以上虛線部分為周期解的不穩定區。若在穩定區上靠近A有一點P，隨著調諧參數σ的不斷增大，點P會沿著曲線AED由點A向點D運動。當調諧參數增大到點D所對應的σ值時，點P會從D點突然跳變到G點，此后再增大σ值，P點將從G點向B點運動。與此相同，若在穩定區上靠近B有一點P，隨著調諧參數σ的不斷減小，點P會沿著曲線BEC由點B向點C運動，當調諧參數減小到點C所對應的σ值時，點P會從C點突然跳變到F點，此后再減小σ值，P點將從F點向A點運動。由此可以看出，當驅動軸的旋轉角速度接近其派生系統的固有頻率的一半時，即在超諧波共振條件下，系統會產生跳躍現象;而且與線性振動系統中最大共振振幅產生在中心頻率不同，在該非線性振動中，系統最大共振振幅并不產生在ω=ω0/2處。圖3與圖4不同，沒有跳躍現象出現。

在圖4產生跳躍現象的區域中，同一調諧參數σ對應于穩定區CEG和DEF上2個不同共振振幅as，即對于同一驅動軸轉速，仍然存在2個穩定的周期解。該現象表明:對于接近于中心頻率ω0/2的某一驅動軸角頻率，其在穩定區CEG和DEF上僅對應一個穩定振幅，該振幅由系統初始條件所決定。

4 不同初始條件下非線性扭轉振動的仿真計算

為驗證非線性扭振系統共振響應對不同初始條件的依賴性，利用式(6）和式(7），對系統超諧波共振振幅進行仿真計算。為與圖4相對應，取ρ=

1）當初始條件為a0=0.8，γ0=0.5時，其共振振幅如圖5(a）所示，其穩定值與圖4中σ=-1時所對應的穩定時的as值基本一致。

2）當初始條件為a0=0.15，γ0=0時，其共振振幅如圖5(b）所示，其穩定值與圖4中σ=-1時所對應的另一穩定時的as值基本一致。

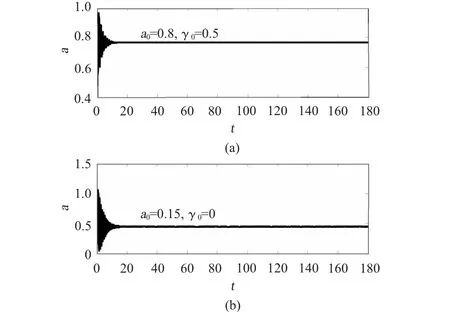
圖5 不同初始條件下的共振振幅 (ρ=0.9，μ/ρ=0.04）Fig.5 The amplitude under different initial conditions(ρ =0.9，μ/ρ=0.04）

5 結語

研究了固有結構偏斜與實際誤差偏斜共同作用下含萬向鉸偏斜轉子系統的非線性扭轉振動問題。在分析從動軸與驅動軸運動學關系的基礎上，推導出偏斜轉子系統的弱非線性扭轉振動方程。利用多尺度法求得該非線性方程在超諧波共振情形下的周期解，并給出穩態周期解的幅頻特性關系式。運用李雅普諾夫第一近似穩定性理論，對系統平衡點進行穩定性研究，得到超諧波共振解振幅隨調諧參數變化的穩定區與不穩定區。最后對不同初始條件下非線性扭轉振動的超諧波共振進行了仿真計算。上述研究表明:

1）固有結構偏斜與實際誤差偏斜的共同作用會引起含萬向鉸轉子系統的非線性扭轉振動，該系統具有形如=0的非自治振動系統形式;

2）在超諧波共振情形下，選取適當的剛度系數ρ、阻尼系數μ時，其幅頻特性曲線會出現跳躍現象，即當驅動軸角頻率ω取某一值時，系統共振振幅發生突變;

3）對于超諧波共振情形，同一調諧參數σ下存在多個振幅與相位;在給定初始條件下，對應于任意驅動軸轉速ω，至多存在一個穩定的共振振幅與共振相位。上述研究結果揭示了含萬向鉸偏斜軸系的非線性動力學基本特性，也為系統進一步的分岔分析奠定了基礎。

［1］PORTER B.A theoretical analysis of the torsional oscillation of a system incorporating a hooke's joint［J］.Journal ofMechanical Engineering Science，1961，3(4）:324 －329.

［2］PORTER B，GREGORY RW.Nonlinear torsional oscillation of a system incorporating a hooke's joint［J］.Journal of Mechanical Engineering Science，1963，5(2）:191 －200.

［3］CHANG S I.Torsional instabilities and nonlinear oscillation of a system incorporating a hooke's joint［J］.Journal of Sound and Vibration，2000，229(4）:993 －1002.

［4］王鴻恩，羅義艮，賀明.三維空間多節萬向傳動軸扭振的分析計算［J］.機械工程學報，2000，36(6）:37 －41.

WANG Hong-en，LUO Yi-yin，HE Ming.Analysis and calculation of torsion vibration of 3－D knottiness hooke's couping［J］.Chinese Journal of Mechanical Engineering，2000，36(6）:37 －41.

［5］朱擁勇，馮昌林，王德石.萬向鉸驅動的偏斜轉子系統運動學分析［J］.機械傳動，2010，34(8）:6 －9，12.

ZHU Yong-yong，FENG Chang-lin，WANG De-shi.The kinematic analysis of misaligned rotor driven by universal joint［J］.Journal of Mechanical Transmission，2010，34(8）:6 －9，12.

［6］劉延柱，陳立群.非線性振動［M］.北京:高等教育出版社，2001:8－18.

LIU Yan-zhu，CHEN Li-qun.Nonlinear vibrations［M］.Beijing:Higher Education Press，2001:8 －18.

Analysis on super-harmonic resonance and stablity of torsional vibration with m isaligned shafts driven by universal joint

ZHU Yong-yong，WANG De-shi，DAIRen-wen
(Department ofWeaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

The nonlinear tosional vibration on rotor system driven by universal joint was studied considering both natural structure misalignment and actual error misalignment.Firstly，the equation with nonlinear vibration was derived.Secondly，the periodic solution was obtained corresponding to superharmonic resonance by multi-scale approach，also the amplitude-frequency characteristic curve.Then the stable regions on the amplitude of the periodic solution were deduced using Lyapunov's approximate stability theory.At last，the calculation simulation were carried outabout super-harmonic resonance of The nonlinear tosional vibration.The results above indicate the fundamental characteristic of the nonlinear dynamic on the misaligned shafts，also applying the foundation for advanced bifurcation and singularity analysis.

torsional vibration;super-harmonic resonance;stablity;misaligned shafts;universal joint

TH133.4

A

1672－7649(2014）05－0089－04

10.3404/j.issn.1672－7649.2014.05.018

2013－03－21;

2013－05－08

國家自然科學基金資助項目(50875259）;海軍工程大學自然科學基金資助項目(HGDQNEQJJ12010）

朱擁勇(1981－），男，博士，主要從事機械動力學、非線性振動研究。