基于回波信號增長率的目標識別方法

譚思煒 任志良

（海軍工程大學兵器工程系，湖北 武漢430033）

引 言

連續波探測系統根據其探測方式可分為主動式和被動式.主動探測系統通常利用回波信號的幅值、相位差和多普勒頻移等特征對目標進行測距、定位［1-3］.但回波信號包絡的增長率特征卻往往被忽略，以至于很少被利用.被動探測系統接收到的目標信號通常為幅度隨距離變化的低頻包絡.目前對于這種信號常用的識別手段多以信號幅值判斷為主［4-5］.同樣缺乏對目標信號增長率特征的有效利用.因而研究基于回波信號增長率的目標識別方法，將有利于提高連續波探測系統的目標識別能力和抗干擾能力.

模擬電路中常用微分電路對信號的時間變化率進行判斷，從而可將有效信號包絡與慢變分量分離開來.雖然微分電路對等幅干擾和慢變干擾有著較好的抑制能力，但對脈沖干擾等快變干擾卻無能為力.目前專門針對連續波探測系統回波信號增長率提取和識別的研究成果相對較少.基于此，提出一種基于回波信號包絡增長率和變化趨勢特征的目標信號識別方法，并以海水中主動式連續波電磁探測系統的回波信號為例，研究該方法的原理及主要性能.

1 目標信號特征分析

1.1 目標信號模型

由于受到目標反射面形狀復雜性和目標方位隨機性的影響，海水中電磁探測系統的目標信號難以用確切的數學公式表示.工程上一般采用理論分析與實際經驗相結合的方式給出計算模型.為方便分析，文獻［6］將目標信號包絡粗略地近似為指數型鐘形函數，并給出了反映目標信號包絡變化規律的歸一化計算公式，如式（1）所示

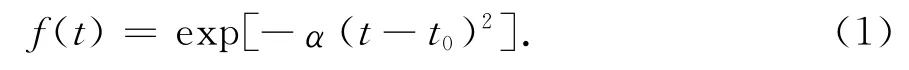
該式將距離等效到時間軸上，即當t＝t0時目標距離最近.式（1）中α為包絡形狀系數，由目標尺度和相對位置關系決定.α可由經驗公式近似表示為

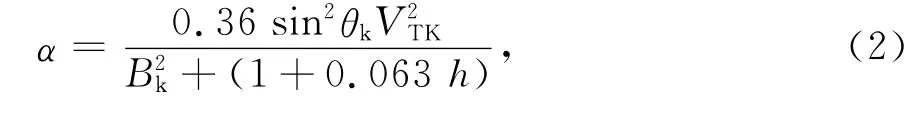
式中：θk為相遇角；VTK為相對速度；h為電磁探測系統的探測距離；Bk為目標反射面的等效寬度.

1.2 包絡曲線特征分析

為簡化分析，考慮相遇角θk＝90°的典型目標信號曲線.對式（1）求一階導數，可得到目標信號包絡曲線f（t）上任意一點的切線斜率，即目標信號包絡的瞬時變化率，如式（3）所示，記為f′（t）.通常情況下，當目標信號包絡幅值達到最大值時，電磁探測系統與目標距離最小.由于接近目標和遠離目標兩種情況下目標信號呈對稱變化，因而只需考慮電磁探測系統接近目標的情況，即目標信號包絡曲線的增長部分.目標信號包絡及其一、二階導數曲線如圖1所示.

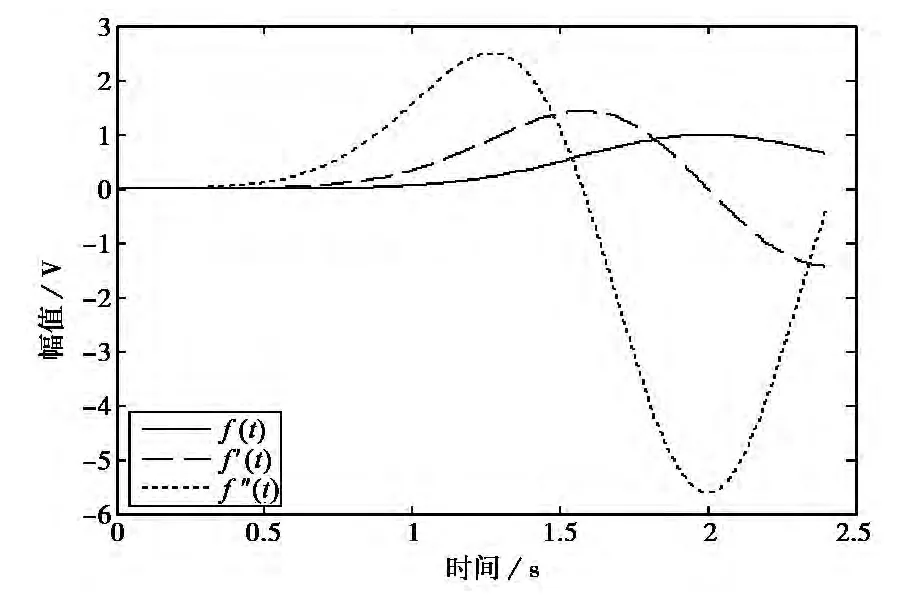
圖1 目標信號包絡曲線及其一、二階導數曲線

歸一化目標信號包絡幅值由0到1變化時，其包絡增長率經歷了先增加后減小的變化過程.這一變化過程在一階導數f′（t）曲線上能夠得到驗證.

f′（t）由0到最大值的過程，是目標信號包絡增長率連續增長到最大的過程.這是因為電磁探測系統感應到的電磁場強度隨著與目標距離的縮短而指數遞增.當距離縮小到一定程度時，包絡增長速度將變緩，即f（t）的增長率逐漸減小.通常情況下，目標反射面尺寸遠大于電磁探測系統輻射器的尺寸，因而接收天線感應到的場強將趨于最大值，即目標信號包絡曲線緩慢趨向最大值［6］，f′（t）逐漸減小為0.通過以上分析不難發現，電磁探測系統與目標距離非常接近時，目標信號包絡增長率的變化特征為逐漸減小到0.

為進一步考察目標信號包絡增長率的變化特征，對式（3）繼續求導，得到原始目標信號包絡曲線的二階導數f″（t），如式（4）所示

對比圖1中曲線f（t）、f′（t）和f″（t）不難發現：當目標信號包絡增長率逐漸增加時，f″（t）的值大于0；反之當目標信號包絡增長率逐漸減小，即包絡曲線增長變緩時，f″（t）的值小于0.

根據以上分析，將電磁探測系統的連續目標信號的包絡變化過程做以下劃分，如圖2所示.

圖2 包絡曲線變化過程的劃分

第Ⅰ階段為AB段，可稱為目標信號包絡幅值的指數上升區.該段上目標信號包絡增長率呈指數遞增，表明目標剛進入電磁探測系統的探測范圍.曲線上B點是目標信號包絡幅值增長率的最大值.該點上，目標信號包絡曲線的二階導f″（t）＝0.從B點開始，目標信號包絡增長率將逐步減小，包絡曲線增長變緩，即f″（t）＜0.

第Ⅱ階段為BC段，可稱為目標信號包絡的線性增長區.從f（t）曲線上看，雖然該段曲線斜率變化不大，但實際上該段目標信號的包絡增長率正逐漸減小，f′（t）呈遞減趨勢，f″（t）＜0.

第Ⅲ階段為CD段，可稱為目標信號包絡幅值的增長飽和區.從f（t）曲線上不難看出，目標信號包絡值正趨于最大，包絡增長率f′（t）逐漸趨于0.此時應為距離最小時，接收天線感應到的電磁場強度趨于最大.

綜上分析，可利用目標信號包絡的一階導數表示包絡的增長率，二階導數表示包絡增長率的變化趨勢，從而根據信號包絡曲線識別目標信號的不同階段.

1.3 包絡增長率的求解分析

實際應用中，包絡曲線是通過接收機等間隔采樣回波信號，并從中提取信號幅值得到的.其得到的是一系列能夠實時反映目標信號包絡變化的離散點.在不考慮采樣誤差和幅值估計誤差的情況下，采用差商法即可從離散點中提取目標信號包絡的增長率和變化趨勢特征，且實時性好.

然而在工程應用中采樣誤差和幅值估計誤差是客觀存在的，主要是因為系統誤差和噪聲干擾的影響.因而實際得到的目標信號包絡曲線是一系列具有一定隨機性和跳躍性的離散點，如圖3所示.

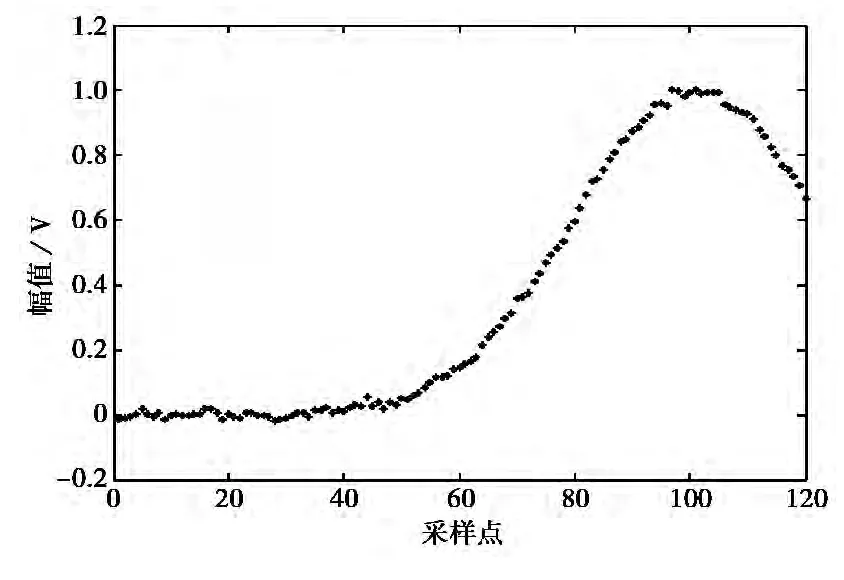
圖3 目標信號包絡曲線采樣

顯然，直接利用這些點來計算包絡的增長率和變化趨勢是非常困難的.這是因為斜率計算對波形的平滑度非常敏感，直接采用差商法計算出的導數誤差非常大.

為真實反映目標信號包絡增長率和變化趨勢，首先采用基于拉格朗日乘數法的多項式擬合算法對采樣信號進行平滑處理，然后再做特征解算.

2 特征求解理論分析

2.1 基于拉格朗日乘數法的曲線平滑

為提高擬合算法的實時性，采用滑動數據窗方式對實驗數據進行處理.窗口中數據段長度保持不變，數據以先入先出的方式逐位更新.這樣既保證了數據處理的實時性，又利用了前后數據的關聯性.采用多項式擬合算法對數據曲線進行平滑處理［7-13］，數據窗每更新一次，就完成一次多項式擬合，并輸出當前窗擬合后第一點數據的校正值，從而實現對目標信號的實時平滑處理.

包絡數據可表示為（ni，xi）（1≤i≤N），其中ni為采樣時刻，xi為采樣數據.數據窗Wi對應的數據區間為［xi，xi＋L-1］，其中i＝1，2，3，…，N-L＋1，設數據窗擬合多項式為

式中：整數m≤L-1；ai，k為待定多項式系數.數據窗W1的擬合多項式p1（n）直接采用傳統最小二乘多項式擬合得到.

從數據窗Wi（i＝2，3，…，N-L＋1）開始，為提高曲線擬合的連續性和光滑性，需在進行多項式擬合時添加如下約束條件

式（6）保證了擬合曲線在（ni，xi）處取值的連續性，而式（7）則利用了一階導數的數學定義保證了擬合曲線在（ni，xi）處的光滑性.

假設

則由式（6）和式（7）可知，多項式擬合的邊界條件應為：Hi＝0和Ki＝0.

令擬合多項式pi（n）對數據窗Wi中ni時刻數據的擬合值與實際采樣值之差為Ri，即Ri＝pi（ni）-xi，則由此可得到新的擬合方程組為

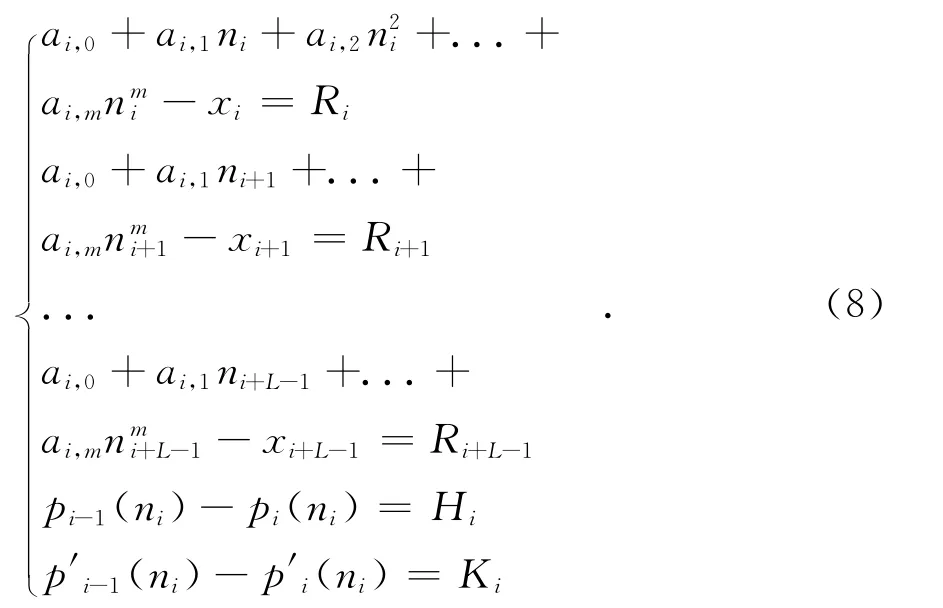
增加了新的約束條件后，傳統最小二乘多項式擬合問題被轉化為多個條件限制的多元函數的極值問題［11-12］，這一類問題通常采用拉格朗日乘數法求解.為此，引入拉格朗日乘數λ1、λ2，則第i個數據窗的拉格朗日函數可表示為

為使曲線擬合誤差最小，即要求拉格朗日函數值Li最小，對式（9）中ai，k和λ1、λ2分別求偏導數，有

式中q＝0，1，2，…，m.

令

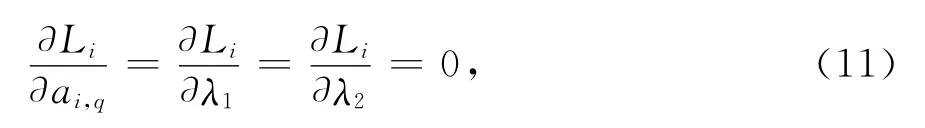
則由式（10）、（11）可分別求出待定多項式系數ai，k（k＝0，1，2，…，m）以及拉格朗日乘數λ1、λ2的值，從而確定數據窗Wi（i＝2，3，…，N-L＋1）的擬合多項式pi（n），并最終確定數據點（ni，xi）的擬合值（ni，pi（ni））.以此類推，數據窗每向前滑動一位，即輸出數據隊列中第一位數據的擬合值，從而依次實現目標曲線的擬合.

2.2 差商法計算離散點導數

擬合后數據點的校正值為（ni，pi（ni）），則可用其一階差商和二階差商來分別表示曲線的一階導數和二階導數

2.3 特征識別

目標信號的特征識別方法示意圖如圖4所示.

圖4 特征識別方法示意圖

其中，d1（B）、d1（C）的值可由實驗測得的典型值確定.數據窗每完成一次數據更新便執行一次以上判別方法，以實現對當前信號特征的及時提取.

3 實驗結果及分析

實驗室條件下，在深5m、寬5m、長7m的水池中，模擬海水中電磁探測系統通過目標時的工作過程.水池中用鹽水模擬海水環境，測得導電率約為7.7Ωm.以長2m、寬2m、厚2cm的鋼板模擬目標反射界面，并用纜繩固定置于水池中.通過上方的滑動導軌，來帶動滑軌2下方1.5m的電磁探測系統，以平行于鋼板平面的方向做直線運動來模擬探測過程.電磁探測系統與鋼板距離取1.2m，如圖5所示.從回波信號中提取到的目標信號包絡如圖3所示.

圖5 實驗示意圖

首先以實驗測得的目標信號包絡曲線為研究對象，并將采用本文算法得到的計算結果與采用文獻［13］中算法得到的結果進行對比.考慮到算法的實時性和擬合效果，折中選取兩種算法的數據窗長度均為L＝5.文獻［13］中算法采用線性插值，取判據SD＝0.1.

3.1 包絡曲線平滑

如圖6（a）所示，本文所采用的擬合法由于在擬合過程中增加了連續、平滑兩個約束條件，因而對解算得到的實際目標信號包絡中的隨機跳動起到了有效的平滑作用，平滑效果比較理想，為隨后的連續增長率計算提供了有利條件.圖6（b）所示的是文獻［13］中算法的擬合結果.可見文獻［13］算法對實驗數據的擬合效果也比較明顯，但在目標信號包絡幅值較小的區域仍有明顯的幅值起伏.

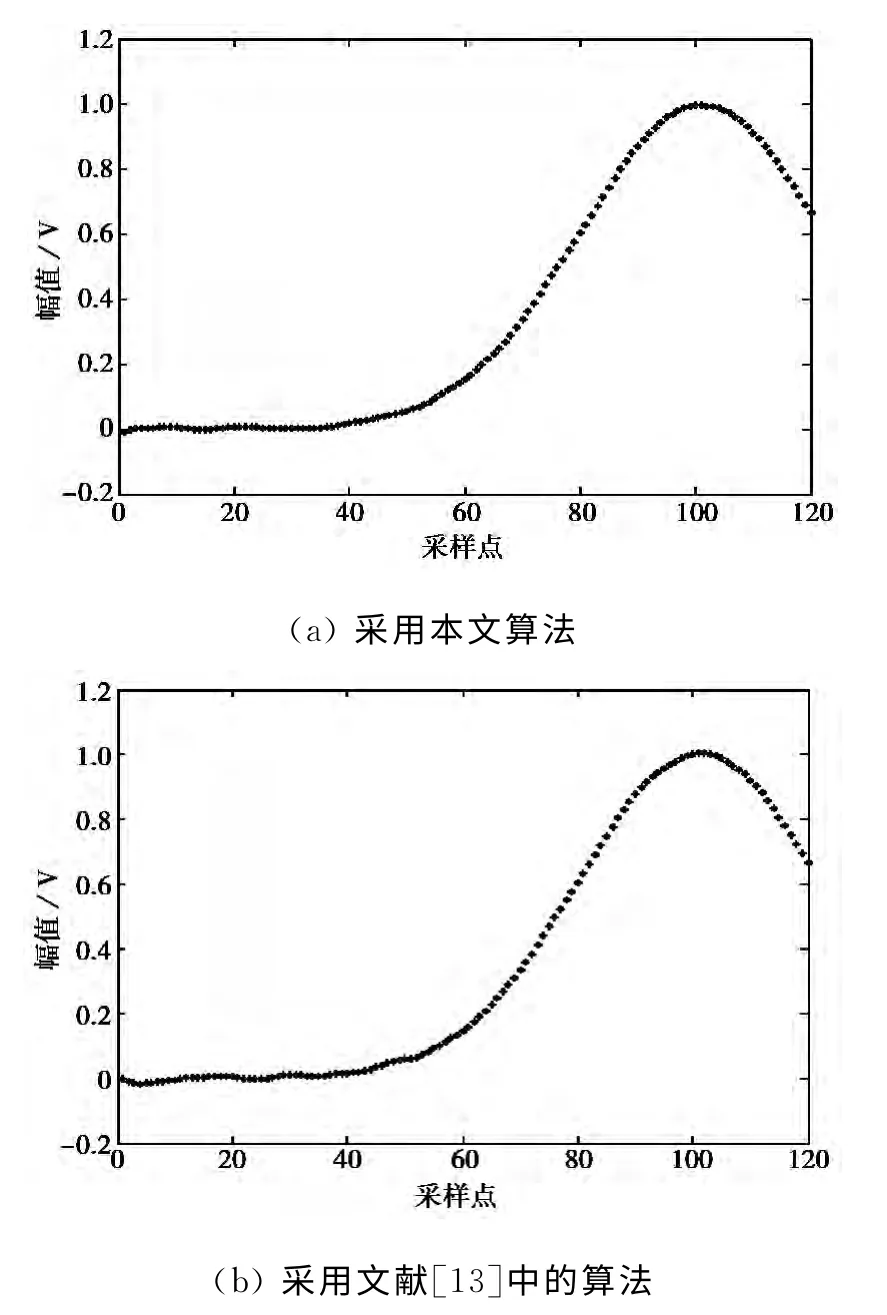
圖6 曲線擬合結果

3.2 包絡增長率計算

采用差商法對經以上兩種算法平滑處理后的數據進行運算，所得到包絡增長率如圖7所示.對比兩圖不難發現，本文采用的平滑算法求得的目標信號包絡增長率的變化規律與理論值較為接近，但仍有明顯的跳動.而文獻［13］中的算法求得的目標信號包絡增長率與理論值相比顯得誤差更為明顯，但能大致反映出包絡增長率的變化規律.這也進一步說明了離散點斜率計算對采樣曲線平滑度非常敏感.

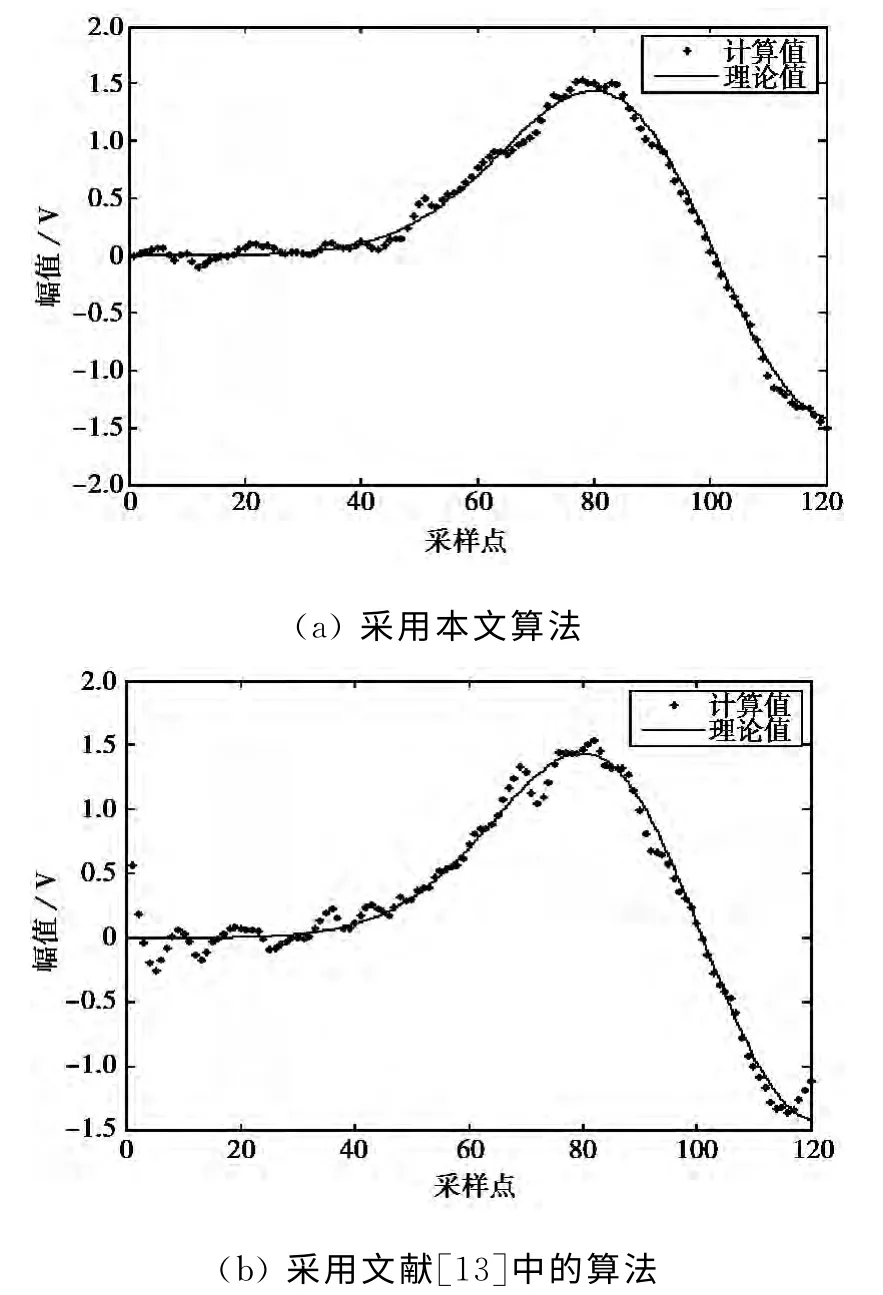
圖7 包絡增長率計算結果

3.3 增長率變化趨勢判斷

首先對解算后的包絡曲線增長率做進一步處理——剔除增長率中誤差明顯較大的點，然后對處理后的包絡增長率變化趨勢進行判斷.判斷標準為：包絡增長率遞增，則變化趨勢判斷結果置1，否則判斷結果置0.不同條件下的判斷結果如圖8所示.

圖8（a）為理論上包絡曲線增長率變化趨勢的判斷結果，圖8（b）為采用本文算法得到的判斷結果，圖8（c）為采用文獻［13］中算法得到的判斷結果.顯然圖8（b）的判斷結果相比圖8（c）更為接近理論值.

3.4 識別率計算

圖8 變化趨勢判斷結果

表1 兩種算法的識別率對比

由表1不難看出，本文提出的目標信號特征識別方法的區間識別率均達到了80%以上，略高于文獻［13］中算法的計算結果.其中，本文算法對增長飽和區的識別率最高，而對線性增長區的識別率最低.這是因為算法對線性增長區的識別主要依賴于對包絡增長率的計算準確度.而增長率的計算準確度卻受到波形平滑程度的直接影響，因而目標信號包絡的平滑度對特征的識別率影響較大.

4 結 論

提出了一種基于回波信號包絡增長率和變化趨勢特征的目標信號識別方法.該方法根據包絡增長率和變化趨勢的不同將目標信號包絡曲線劃分為指數上升、線性增長和增長飽和三個階段.并利用基于拉格朗日乘數法的滑動數據窗多項式擬合算法與差商法聯合求解出包絡曲線增長率和變化趨勢特征.算例表明，該方法對目標信號包絡曲線三個部分的識別率分別達到88.2%、82.7%和91.3%，因而能夠實現對回波目標信號的有效識別.

本文所設計的目標識別方法可廣泛應用于水下近場電磁探測系統的目標識別、連續波雷達探測以及計算機圖形識別等領域，為提高目標信號的特征識別能力和抗干擾性能提供了參考.

［1］郭琨毅，張永麗，盛新慶，等.基于欠定盲分離的多目標微多普勒特征提取［J］.電波科學學報，2012，27（4）：691-695＋759.GUO Kunyi，ZHANG Yongli，SHENG Xinqing，et al.An approach for extracting independent micro-Doppler characteristics of multiple targets based on underdetermined blind source separation［J］.Chinese Journal of Radio Science，2012，27（4）：691-695＋759.（in Chinese）

［2］侯 志，繆 晨，張金棟，等.復雜探測背景下的LFMCW雷達目標二維檢測方法［J］.西安電子科技大學學報：自然科學版，2011，38（4）：167-172.HOU Zhi，MIAO Chen，ZHANG Jindong，et al.Moving target detection and processing method of LFMCW radar under complex background［J］.Journal of Xidian University：Science and Technology，2011，38（4）：167-172.（in Chinese）

［3］劉貴喜，凌文杰，楊萬海.線性調頻連續波雷達多目標分辨率的新方法［J］.電波科學學報，2006，21（1）：79-83.LIU Guixi，LING Wenjie，YANG Wanhai.Novel method to multitarget resolution for linear frequencymodulated continues wave radar［J］.Chinese Journal of Radio Science，2006，21（1）：79-83.（in Chinese）

［4］YU Bo，LIU Yanchun，ZHAI Guojun，et al.Magnetic detection method for seabed cable in marine engineering surveying［J］.Geo-spatial Information Science，2007，10（3）：186-190.

［5］王 靜，黃建國，張群飛，等.噪聲空間譜預白化小孔徑陣列被動目標檢測方法［J］.西北工業大學學報，2012，30（3）：422-427.WANG Jing，HUANG Jianguo，ZHANG Qunfei，et al.An effective noise spatial spectrum pre-whiten approach in passive detection using small aperture array［J］.Journal of Northwestern Polytechnical，2012，30（3）：422-427.（in Chinese）

［6］王紹卿，劉健民.魚雷近炸引信原理與設計［M］.西安：西北工業大學出版社，1992.

［7］CHENG Lerong，XIONG Jinjun，HE Lei.Non-Gaussian statistical timing analysis using second-order polynomial fitting［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2009，28（1）：130-140.

［8］PANG Xufang，SONG Zhan.Detecting and classifying umblic points from polynomial fitting point cloud［C］／／2011IEEE International Computational Conference on Science and Engineering.Dalian，August 24-26，2011：155-160.

［9］WANG Y，WANG D S，BRACKSTEIN A M.On variational curve smoothing and reconstruction［J］.Journal of Mathematical Imaging and Vision，2010，37（3）：183-203.

［10］AZAR R Z，GOKSEL O，SALCUDEAN S E.Subsample displacement estimation from digitized ultrasound RF signals using multi-dimensional polynomial fitting of the cross-correlation function［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2010，57（11）：2403-2420.

［11］王 可，唐忠輝，孫興偉.一種點云數據曲線光順處理算法［J］.組合機床與自動化加工技術，2013，（2）：64-66＋69.WANG Ke，TANG Zhonghui，SUN Xingwei.A curve fairing processing algorithms of point cloud data［J］.Modular Machine Tool ＆Automatic Manufacturing Technique，2013，（2）：64-66＋69.（in Chinese）

［12］張 勇，林 皋，胡志強，等.等幾何分析方法求解靜電場非齊次邊值問題［J］.電波科學學報，2012，27（5）：997-1004.ZHANG Yong，LIN Gao，HU Zhiqiang，et al.Isogeometric analysis for electrostatic problem with inhomogeneous boundary conditions［J］.Chinese Journal of Radio Science，2012，27（5）：997-1004.（in Chinese）

［13］王玉詔，張寅超，陳思穎，等.用于激光雷達回波平滑的半步長插值迭代法［J］.北京理工大學學報，2011，31（12）：1424-1427.WANG Yuzhao，ZHANG Yinchao，CHEN Siying，et al.Half-step interpolation iteration method for smoothing echo from atmosphere lidar［J］.Transactions of Beijing Institute of Technology，2011，31（12）：1424-1427.（in Chinese）