電離層相位污染和多模傳播檢測與識別研究

李 雪 柳 文 李吉寧 孫鳳娟 李川川

（中國電波傳播研究所，山東 青島266107）

引 言

天波超視距雷達（Over-The-Horizon Radar，OTHR）利用電離層作為傳輸介質，可實現幾千千米外的超視距目標探測.電離層是時變、隨機、色散和各向異性的介質，影響雷達信號傳播，特別是電離層相位污染、多模傳播引起OTHR雜波頻譜展寬，嚴重制約低速目標檢測［1］.針對這一問題，近年來開展了諸多研究.

相位污染引起的雜波頻譜展寬，主要采用時域估計補償方法解決，比較流行的算法有最大熵譜估計法［2］、相位梯度 估計法［3］、時頻 分析法［4］、特征分解法［5］和分段多項式相位建模法［6］等.

多模傳播引起的雜波頻譜展寬，主要采用以下三種方法解決：

1）基于二維天線陣列

OTHR采用二維天線陣列，利用俯仰方向上的波束形成使雷達工作于單一傳播模式，但為了滿足一定的俯仰、方位分辨率，造價極高.

2）基于工作頻率選擇

OTHR電離層自適應診斷管理系統實時選擇合適的工作頻率，可以最大可能地避免多模式傳播效應.但考慮對探測目標覆蓋及環境干擾等信息，有時不能選擇出單模工作頻率.

3）基于信號處理技術

當不能從天線結構和頻率選擇上解決多模傳播問題時，就需要考慮采用信號處理技術.文獻［7］提出利用海雜波循環對消去除多個Bragg峰，從而發現目標.

若電離層相位污染和多模同時存在，上述方法均失效.文獻［7］提出利用高分辨時頻分布直接實現目標檢測.

通過上述分析可以看出，僅存在相位污染、僅存在多模傳播以及二者共存抑制方法完全不同.錯誤地使用不同類型的抑制方法，將無法獲得期望的處理增益，甚至會惡化目標檢測能力.同時，若回波數據不存在相位污染和多模傳播，仍采用解相位污染和解多模處理，不但增加大量的無效數據處理，影響系統的實時性，還可能惡化未受污染的回波數據.

綜上所述，若想有效抑制電離層引起雜波頻譜展寬，必須實現回波數據下述四類情形檢測與識別：

I無相位污染，無多模傳播；

II僅存在相位污染；

III僅存在多模傳播；

IV相位污染和多模傳播共存.

國內外關于這一問題研究較少，文獻［8］在滿足相鄰距離、方位單元污染函數相同模型假設條件下提出一種時間可逆算法檢測相位污染，但不能檢測多模，無法實現上述四類情形識別.

本文在時間可逆法基礎上，提出特征分解法檢測多模傳播，級聯使用時間可逆法和特征分解法實現I、III類情形識別，并可估計傳播模式數目.提出了一種基于回波序列Hankel矩陣特性檢測相位污染和多模傳播算法，可實現I、III類情形識別、模式數目估計，且無需相鄰距離、方位單元污染函數相同模型假設.首次提出基于返回散射探測多模傳播檢測算法，聯合時間可逆法或Hankel矩陣算法實現II、IV類情形識別.

1 電離層相位污染檢測方法

1.1 時間可逆法檢測相位污染

OTHR在進行解電離層相位污染之前，可以通過考察回波信號序列的時間可逆性來檢驗是否存在相位污染.

假設來自K個相鄰距離、方位單元的回波信號受到相同的相位污染.其中第k個距離單元上的回波序列表示為

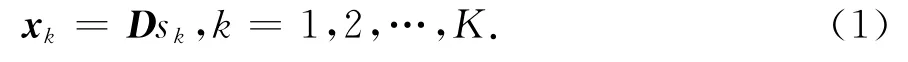
式中：sk為未受污染的回波序列；D稱為模糊矩陣，分別表示為：

式中：TR為脈沖重復周期；N為一個相干積累時間（Coherent Accumulative Time，CIT）內脈沖重復周期的個數.φ（n）（n＝0，1，…，N-1）為相位污染函數.注意φ（n）中不包含任何線性分量，因為線性分量只會使多普勒譜平移，而不是展寬.

用K個回波序列分別構成數據矩陣X的每一列，矩陣的維數是N×K，得到協方差矩陣R＝XXH／K，其時間可逆性指R＝JR＊J，其中J為交換矩陣，JR＊J稱為R的時間逆矩陣.回波信號滿足時間可逆性的充分必要條件是對角矩陣D也滿足該性質，即D＝JD＊J.

充分條件理論推導如下

設RS＝SSH，則

已知RS＝J，則

由于J2＝I（I為單位矩陣），因此，

而

將式（6）代入式（7）得

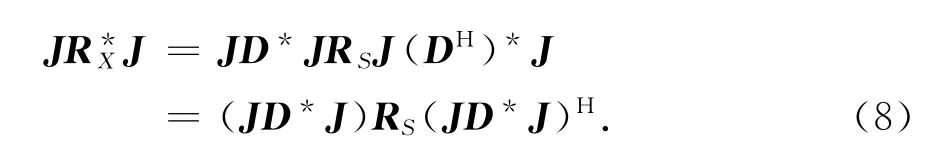
上式的推導利用了交換矩陣J的性質JH＝J.由式（8）可見，當D＝JD＊J時有

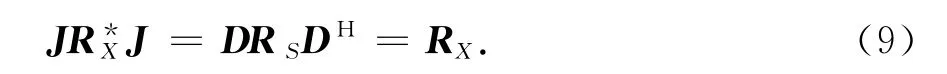
即回波信號滿足時間可逆性.

必要條件理論推導如下

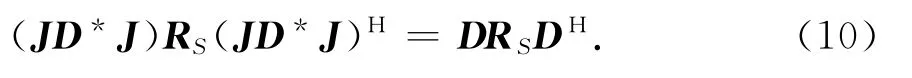
左乘D-1，右乘（DH）-1，可得

由此可推出

即

從上述推導可知，當回波信號滿足時間可逆性時，對角矩陣D滿足時間可逆性，回波信號未經歷相位污染；當回波信號不滿足時間可逆性時，對角矩陣D也不滿足時間可逆性，回波信號存在相位污染.這就給出了回波信號是否存在相位污染的一個判據.實際應用中，通常通過檢驗信號協方差矩陣的噪聲子空間與其時間逆矩陣的信號子空間是否正交來判斷.

若雜波頻譜展寬由多模傳播引起，則未受污染回波序列為

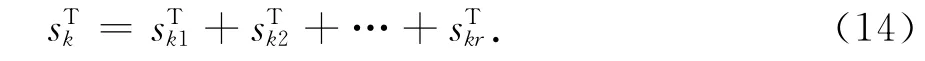
式中r表示模式數目，回波序列協方差矩陣為

即各傳播模式自協方差矩陣和互協方差矩陣之和.由于各傳播模式回波不相關，故互協方差矩陣為零.而各模式自相關矩陣滿足時間可逆性，因此無法利用該方法實現多模傳播檢測.

1.2 特征分解法檢測多模傳播

根據現代譜估計理論，信源數目與回波信號協方差矩陣主特征值數目相對應.若回波不存在相位污染，考慮一階海雜波正負峰成對出現，則回波協方差矩陣主特征值數目為傳播模式數目兩倍.依據此特性可實現多模傳播檢測及傳播模式數目估計.

若回波信號存在相位污染，其時間平穩性受到破壞，即使不存在多模傳播，主特征值數目仍為多個，此時該方法不能檢測多模傳播.顯然，單獨應用該方法也不能實現上述四類情形識別.

1.3 時間可逆法與特征分解法的級聯應用

通過前面分析可以看出，時間可逆法僅能檢測相位污染，但不能實現多模傳播檢測.特征分解法雖能實現多模傳播檢測，但需已知回波不存在相位污染.

若先利用時間可逆法檢測出回波信號未受相位污染，再利用特征分解法檢測多模傳播，則可實現上述第I、III類情形識別.但正如前面所分析，該方法要求相鄰距離、方位單元雜波數據需滿足獨立同分布序列，污染函數需滿足同一性模型假設.

1.4 Hankel矩陣法檢測相位污染和多模傳播

有時，電離層相位污染較為嚴重，回波數據不滿足相鄰距離、方位單元污染函數同一性模型假設.此時，級聯算法失效.本文首次提出一種基于回波時間序列Hankel矩陣的相位污染、多模傳播檢測方法，可實現I、III類情形識別，且無需上述假設條件.

假設信號s（n）由r個時變復正弦分量疊加組成

式中：Ai為信號幅度；φi為信號相位，i＝1，…，r.每條曲線的瞬時頻率為

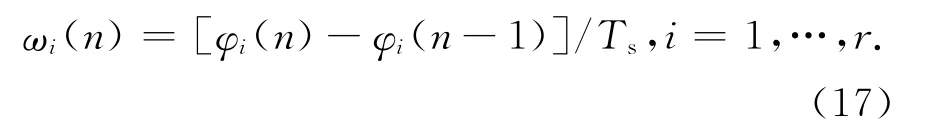
式中：ωi為信號瞬時頻率；Ts為采樣間隔.

考慮由s（n）時間序列構造的Hankel矩陣：

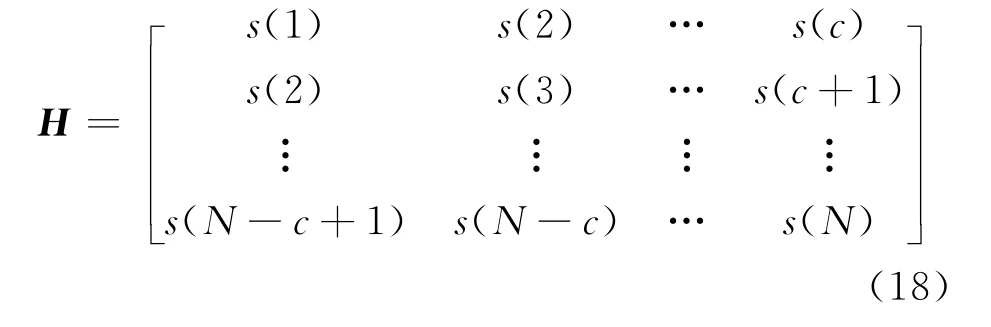
式中c＝3r表示矩陣列數，文獻［9］給出了該矩陣的幾個性質.

性質1：當復正弦分量頻率為常量時，Hankel矩陣的秩為r.

性質2：當復正弦分量頻率是時變時，Hankel矩陣為滿秩.

顯然，式（16）可用于表示OTHR回波零中頻信號，r表示海雜波一階峰數目.當回波信號存在電離層相位污染時，頻率是時變的，回波信號構造的Hankel矩陣為滿秩；當回波信號不存在電離層相位污染時，頻率是常量，回波信號構造的Hankel矩陣秩為r，因此該方法可用于判斷電離層相位污染是否存在.

當不存在電離層相位污染時，根據回波時間序列構造的Hankel矩陣的秩表征了回波信號數目，考慮海雜波一階峰成對出現，則傳播模式數目為r／2.若r／2＞1，則為多模式傳播.Hankel矩陣秩的一半為傳播模式數目.因此，該方法可用于電離層相位污染不存在情況下的多模傳播檢測.該方法與級聯應用時間可逆法和特征分解法相比，具有更小的計算量，且使用條件更加寬泛.但正如文獻［9］指出，該方法易受噪聲影響.OTHR地海雜波回波能量較強，雜噪比通常在50dB之上，有時甚至達70～80dB，因此可忽略噪聲影響.若由于電離層吸收或工作頻率過低引起雜噪比下降時，使用前應先對噪聲進行抑制.文獻［9］采用奇異值分解方法對噪聲進行了抑制，取得較好效果.通過上述分析可以看出，基于時間可逆法和特征分解法的級聯算法、Hankel矩陣法均僅能實現I、III類型識別，當電離層存在相位污染時，無法判別多模傳播是否存在，即不能實現II、IV類型識別.

1.5 基于返回散射傳播模式區提取的多模傳播檢測

返回散射探測是OTHR最重要的電離層環境探測手段，其探測路徑與雷達信號路徑相同.通過對返回散射掃頻探測結果處理，可獲得覆蓋區內全頻段傳播模式信息，圖5（c）是典型的兩層返回散射電離圖.顯然，根據各傳播模式區域信息，可實現某一工作頻率、距離單元回波多模傳播檢測.該方法與時間可逆法（或Hankel矩陣法）級聯使用，可實現II、IV類情形識別.基于返回散射探測傳播模式區提取的多模傳播檢測方法與特征分解法、Hankel矩陣法相比，引入新信息源，在回波信號存在相位污染情形下仍可有效檢測多模.但該方法不能準確估計模式模糊區的傳播模式數目.

2 實測數據驗證

高頻返回散射定頻探測數據與OTHR回波數據特性相同，可利用其進行上述算法驗證.

2.1 I類情形檢測與識別驗證

圖1為某高頻返回散射探測站定頻地物回波功率譜，工作頻率9.656MHz，群距離700km，脈沖重復頻率40Hz，相干積累時間12.8s，頻譜形成過程中，為了抑制多普勒旁瓣，添加了漢明窗.從圖中可獲得頻譜最高譜峰3dB寬度為0.12Hz，與無相位污染條件下回波頻譜寬度理論值0.114Hz幾乎相同.可確定該距離單元回波既不存在相位污染，也不存在多模傳播，符合I類情形.分別采用Hankel矩陣算法和級聯應用時間可逆法、特征分解法處理回波數據，其中Hankel矩陣列數取為9，設A表示回波信號時間逆矩陣信號向量和協方差矩陣噪聲向量的內積均值，取K＝0.01表示正交門限值，定義M表示主特征值數目，N表示傳播模式數目，判斷結果如表1所示.

圖1 返回散射定頻探測譜圖

表1 相位污染、多模傳播檢測與識別

2.2 II類情形檢測與識別驗證

圖2（a）為2010年3月30日7時31分某高頻返回散射探測站定頻地物回波頻譜數據，工作頻率8.726MHz，群距離780km，脈沖重復頻率20Hz，相干積累時間51.2s.圖2（b）為取前12.8s數據進行相干積累獲得的譜圖，顯然，圖形中僅存在一個譜峰，且頻譜峰值3dB寬度為0.17Hz，略大于無相位污染條件下回波頻譜寬度理論值0.114Hz，故圖2（b）所示頻譜僅存在較小相位污染，未受多模傳播影響.綜合上述分析，可確定圖2（a）所示頻譜存在相位污染，但不存在多模傳播，符合II類情形.分別采用時間可逆法和Hankel矩陣算法檢測相位污染，其中Hankel矩陣列數取為9，判斷結果如表2所示.由于相位污染存在，此時只能采用基于返回散射傳播模式區提取檢測多模傳播.圖3為2010年3月30日7時30分55秒探測的掃頻電離圖，其波束指向與圖2（a）相同.圖中黑色“＋”為工作頻率8.726MHz、群距離780km對應的位置，顯然，該距離單元回波為單模傳播，判斷結果如表2所示.

圖2 返回散射定頻探測頻譜圖

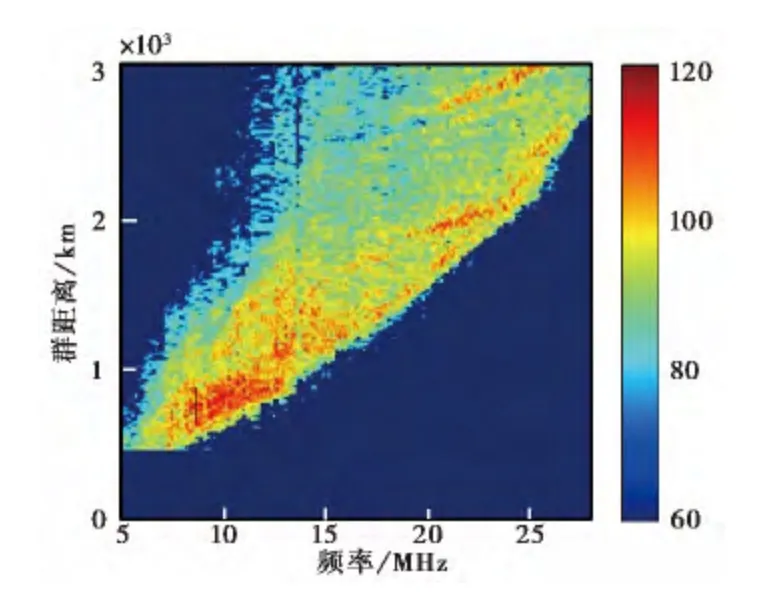
圖3 返回散射掃頻探測圖

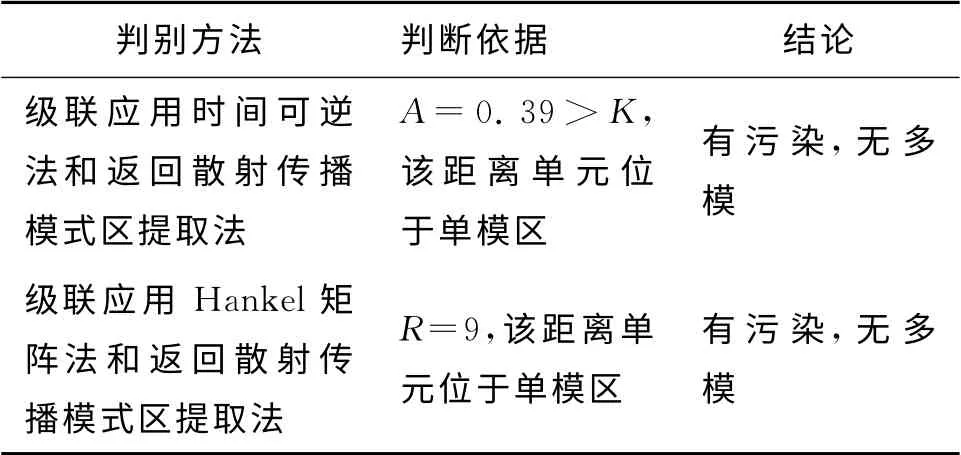
表2 相位污染、多模傳播檢測與識別

2.3 III類情形檢測與識別驗證

圖4為2010年5月12日13時45分某高頻返回散射探測站定頻地物回波功率譜，工作頻率8.532MHz，群距離850km，相干積累時間6.4s，脈沖重復頻率20Hz.顯然，該回波數據存在多模式傳播，同時該組試驗數據錄取于中午時段，電離層較為穩定，且相干積累時間較短，各譜峰3dB寬度與理論值基本相同，故該組數據不存在相位污染，屬于第III類情形.分別采用Hankel矩陣算法和級聯應用時間可逆法、特征分解法處理回波數據，其中Hankel矩陣列數取為9，判斷結果如表3所示.

圖4 返回散射定頻測譜圖

表3 相位污染、多模傳播檢測與識別

2.4 IV類情形檢測與識別驗證

圖5（a）為2009年5月17日15時31分0秒探測的返回散射探測定頻海洋回波功率譜，工作頻率12.077MHz，群距離1 250km，脈沖重復頻率20 Hz，相干積累時間51.2s.圖5（b）為取前6.4s進行相干積累獲得的頻譜圖，其峰值3dB寬度為0.23Hz，略大于理論值，從圖中可明顯看出存在兩個傳播模式.綜合上述分析，圖5（a）所示頻譜多模與相位污染共存，屬于IV類情形.采用時間可逆法和Hankel矩陣法檢測電離層相位污染，其中Hankel矩陣的列數取為12，判斷結果如表4所示.由于相位污染存在，此時只能采用基于返回散射傳播模式區提取檢測多模傳播.圖5（c）為2009年5月17日15時30分55秒探測的返回散射掃頻圖.圖中黑色“＋”為工作頻率12.077MHz、群距離1 250km對應的位置，顯然，該距離單元回波存在多模傳播.故該回波數據多模傳播與相位污染共存.

圖5 返回散射掃、定頻探測圖形

表4 返回散射實測數據相位污染檢測

3 結 論

綜合應用時間可逆法、特征分解法、Hankel矩陣法、基于返回散射傳播模式提取的多模傳播檢測與識別算法，可實現I、II、III、IV類情形識別，為后續信號處理選擇相應類型抑制算法提供依據.實際應用中，首先采用時間可逆法或Hankel矩陣法判別回波數據是否存在相位污染：若不存在相位污染，則采用特征分解法或Hankel矩陣法進行多模傳播檢測；若存在相位污染，則采用返回散射傳播模式提取算法實現多模傳播檢測.

［1］凡俊梅，焦培南，肖景明.海洋雜波對高頻雷達檢測海面上低速目標的影響［J］.電波科學學報，1997，12（2）：205-210.FAN Junmei，JIAO Peinan，XIAO Jingming.The sea clutter effect on the low doppler targets detection by HF radar［J］.Chinese Journal of Radio Science，1997，12（2）：205-210.（in Chinese）

［2］BOURDILLON A，GAUTHIER F，PARENT J.Use of maximum entropy spectral analysis to improve ship detection by over-the-horizon radar［J］.Radio Science，1987，22（2）：313-320.

［3］邢孟道，保 錚.電離層電波傳播相位污染校正［J］.電波科學學報，2002，17（2）：129-133.XING Mengdao，BAO Zheng.Phase perturbation correction in ionospheric electromagnetic wave propagation［J］.Chinese Journal of Radio Science，2002，17（2）：129-133.（in Chinese）

［4］HOWLAND P E，COOPER D C.Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems［J］.IEEE Proceedings-F，1993，140（1）：29-36.

［5］ANDERSON S J，ABRAMOVICH Y I.A unified approach to detection，classification，and correction of ionospheric distortion in HF sky wave radar systems［J］.Radio Science，1998，33（4）：1055-1067.

［6］李 雪，鄧維波，焦培南.分段多項式建模解電離層慢徑相位污染階數選擇新方法［J］.電波科學學報，2009，24（6）：1-6.LI Xue，DEND Weibo，JIAO Peinan.New orderselect method of polynomial modeling for ionosphere phase perturbation correction［J］.Chinese Journal of Radio Science，2009，24（6）：1-6.（in Chinese）

［7］郭 欣.天波超視距雷達信號處理技術研究［D］.南京：南京理工大學，2004.GUO Xin.Study on Skywave Over-the-horizon Radar Signal Processing［D］.Nanjing：Nanjing University of Scienee and Technology，2004.（in Chinese）

［8］ABRAMOVICH Y I，ANDERSON S J，SOLOMON I S D.Adaptive ionospheric distortion correction techniques for HF skywave radar［C］／／Proceedings of 1996 IEEE National Radar Conference.Ann Arbor，1996：267-272.

［9］DIMONTE C L，ARUN K S.Tracking the frequencies of superimposed time-varying harmonics［C］／／Proceedings of 1990IEEE National Radar Conference，1990：2539-2542.