3點Binary插值細分法的性質以及應用

黃樹培， 鄭紅嬋， 閆飛一， 胡 韻

（西北工業大學應用數學系，陜西 西安 710129）

3點Binary插值細分法的性質以及應用

黃樹培， 鄭紅嬋， 閆飛一， 胡 韻

（西北工業大學應用數學系，陜西 西安 710129）

為了使細分格式具有好的性質：如光滑性、保凸性，提出了 3點 binary插值細分格式，然后分析了該細分格式的連續性、保凸性以及分形等性質與參數之間的關系，最后給出了該細分格式性質的一些應用。

插值細分格式; 連續性; 保凸性; 分形性質

細分是一種有效的曲線曲面造型技術。由于具有算法簡單、易于實現等優點，因此廣泛地應用于計算機圖形學、計算機輔助幾何設計、計算機動畫、逆向工程以及醫學圖像處理等領域。

細分格式根據極限曲線曲面是否經過初始控制頂點，可分為插值細分格式和逼近細分格式。通常逼近細分格式生成的極限曲線更光滑，例如Siddiqi和Ahamd[1]提出了3點binary逼近細分格式，其極限曲線是 C2連續的；Siddiqi和Rehan[2]提出了一個改進的4點binary逼近細分格式，其極限曲線可以達到 C5連續。由于具有插值的性質，因此在實際應用中插值細分格式比逼近細分格式更有吸引力。Dyn等[3]提出了 4點binary插值細分格式，其極限曲線是C1連續的；Weissman[4]提出了6點binary插值細分格式，其極限曲線可以達到 C2連續。在這基礎上，后來又出現了一些其他改進的binary插值細分格式如蔡志杰[5]，并分析了其光滑性等基本性質。

Bézier方法是一種幾何造型方法，其優點是具有保形性，但其缺點之一是不具有插值性質，于是為了滿足插值性質以及保形性質，丁友東和華宣積[6]提出了一類保凸的非線性插值細分格式。

在分形理論中，分形的生成時非常重要的。有很多方法可以用來生成分形，例如，Bahar[7]利用函數迭代系統的方法；Prusinkiewicz和Lindenmayer[8]利用L系統的方法；齊東旭和戈建濤[9]利用細分的方法等。

在實際應用中有時要求極限曲線具有好的性質：如光滑性、局部性和保凸性等。于是本文構造了一個3點binary插值細分格式，其極限曲線是 C1連續的。該細分格式具有好的性質：局部性，3點細分格式的支撐寬度是 4，Dyn等[3]

中的4點插值細分格式是也 C1連續的，但其支撐寬度是6。保凸性：當給定的初始數據為嚴格凸時，3點binary插值細分格式的細分參數滿足一定條件時，極限曲線也是凸的。同時還可以發現細分曲線的形狀與細分參數有一定的關系，可以控制曲線的膨脹與收縮，而且當細分參數在一定的條件下時，細分格式可以產生分形曲線。

1 預備知識

其中 J0為初始有序控制頂點的有限下標集，設

為第k次細分后的有序控制頂點集， Jk為相應的有限下標集。均勻穩定的binary細分法可表示為：

定義1 由 maskα 確定的多項式稱為細分法S的生成多項式。

定理1[10]若細分法S一致收斂，則其，滿足

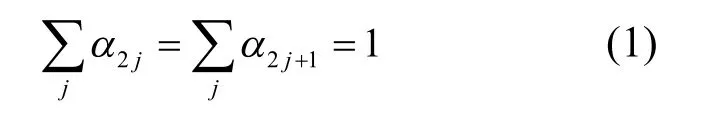
細分法的收斂性與光滑性分析可歸結為向量值函數的分量的收斂性與光滑性分析，而每個分量是由同一細分法產生的標量函數，因此只需要對初始控制實數集進行分析。

定理2[10]設細分法S的滿足式(1)，則存在一個細分法 S1，滿足

S1稱為S的一階均差細分法,S稱為基細分法。 S的 n階均差細分法 Sn的 mask為則 其 生 成 多 項 式 為

定理3[10]細分法S一致收斂當且僅當細分法對任何初始數據一致收斂于0。

定理4[11]設細分法S的maskα滿足式(1)。若 存 在 正 整 數L及 實 數 c, 0 ≤ c＜1,使則細分法S一致收斂。

根據定理1和定理4，當細分法S及其i階均差細分法 Si（i = 1,2,… ,n ）的 mask和分別滿足

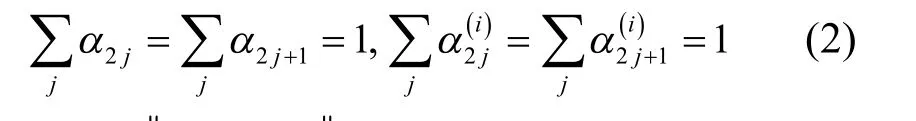
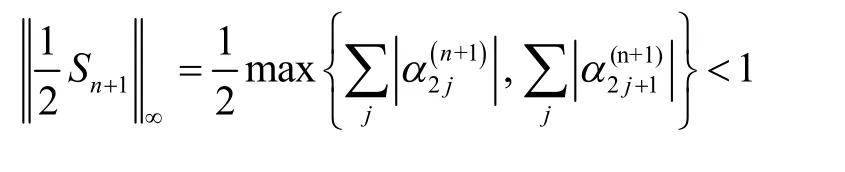
2 3點Binary插值細分格式

下面給出單參數的3點binary插值細分格式：

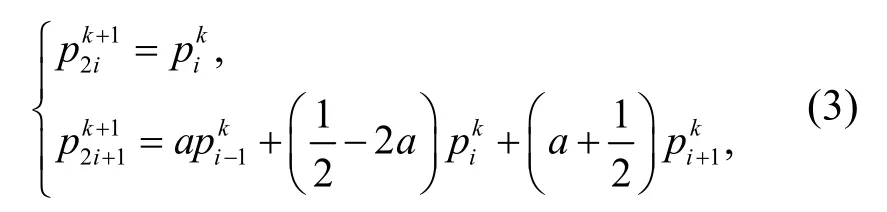
經過變形可化為：

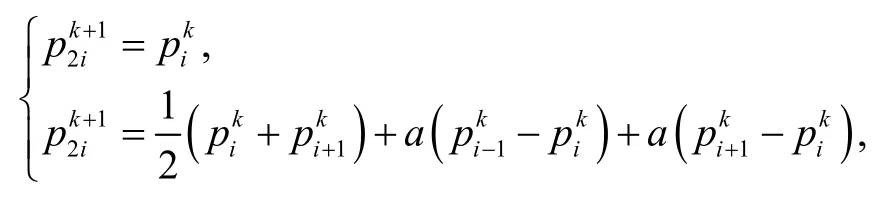
其中，a為細分參數。

3 3點Binary插值細分格式的性質

下面研究本文提出的3點binary插值細分格式的性質：光滑性、保凸性以及分形性質。

3.1 連續性

下面利用生成多項式的方法來分析 3點binary插值細分格式的連續性。

因為滿足式(1)，故有

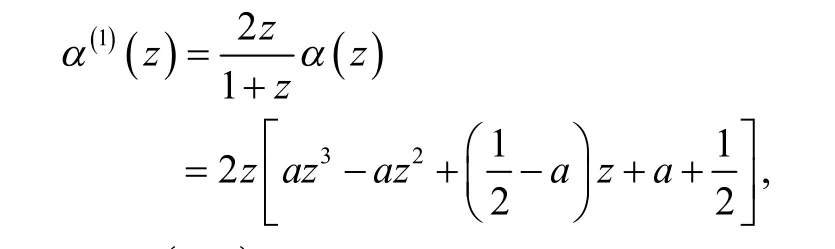
因為 α（1）滿足式(2)，故有

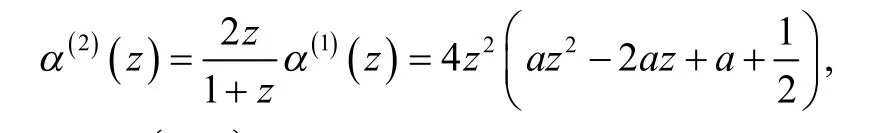
實驗發現：當 a＜ 0時，極限曲線向外膨脹；當 a＞ 0時，極限曲線向內收縮；當 a= 0時，極限曲線為初始控制多邊形。

3.2 保凸性

定理5 當初始數據是嚴格凸時，3點插值細分格式是保凸的。

利用二階差分定義：

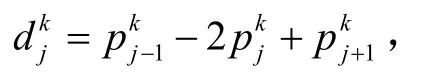
得到相應的二階差分格式：

其中

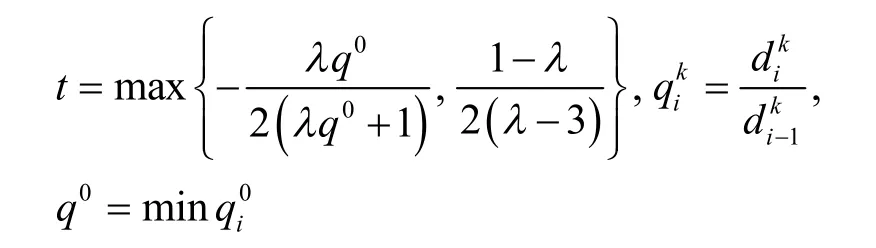
證明由于而因此，當 a＜ 0時，＞ 0。

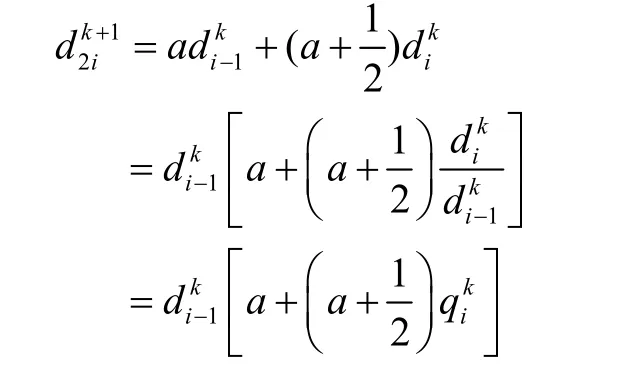
假設k時，命題成立。下面證明 k+1時，命題也成立。

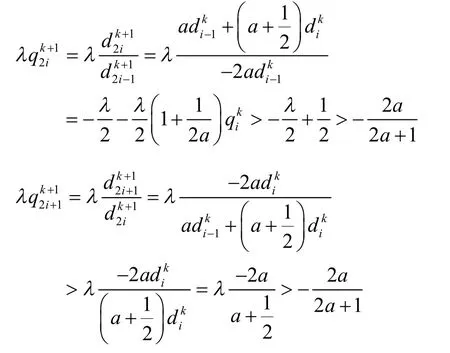
因此，該細分格式對于嚴格的凸數據是保凸的。

3.3 分形性質

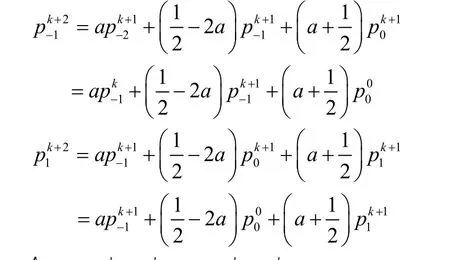
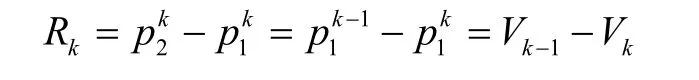
即

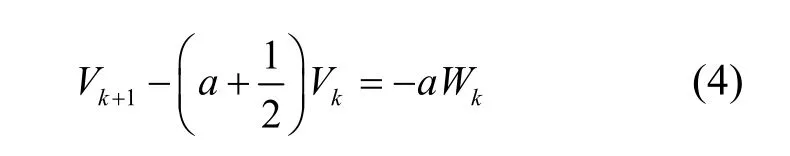
相應的特征方程是：

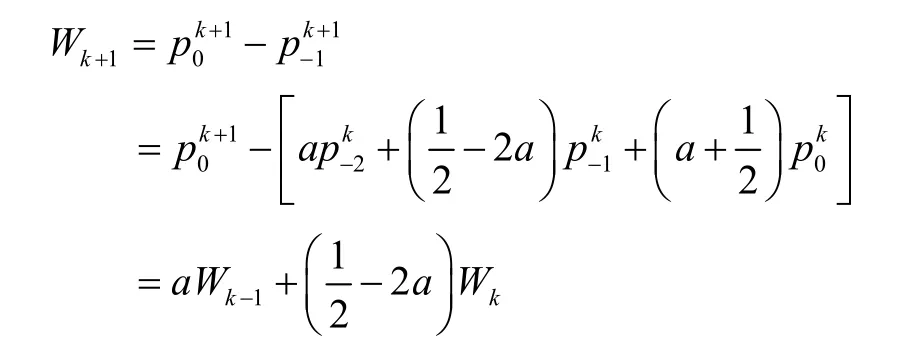
即

相應的特征方程是：

由于初始條件

可知式(6)的特解為

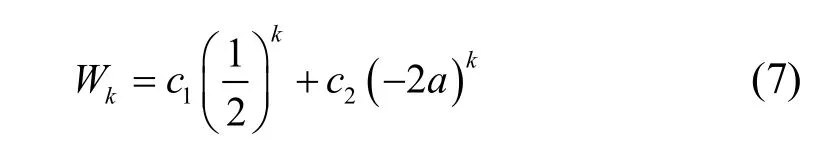
其中

由式(7)可知，式(4)可化為

其特解為

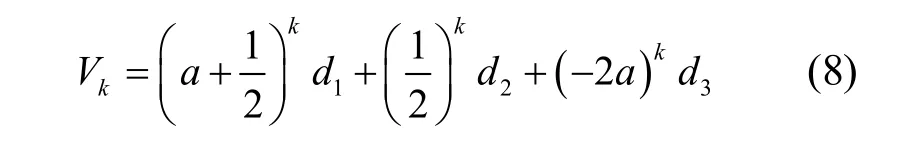
其中

由于

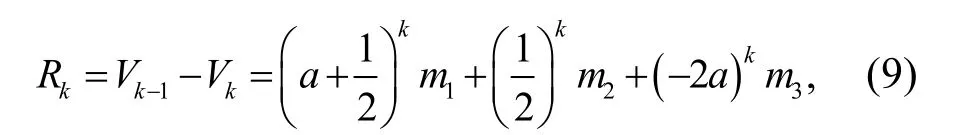
其中

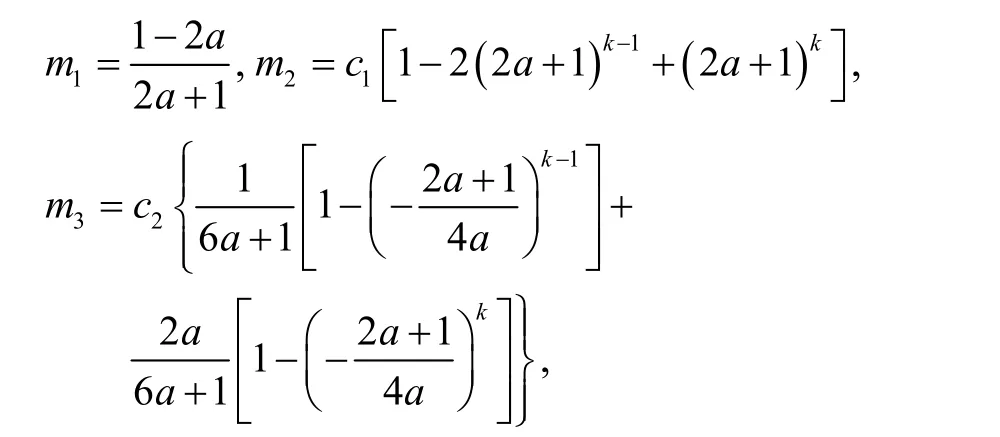
c1,c2同式(7)。

定理6 當0＜ a＜時，3點binary插值細分法的極限曲線是分形曲線。

證明當0＜ a＜時，由式(8)和式(9)歸納推理可知，經k次細分后位于和之間的2k個小邊向量可表示為

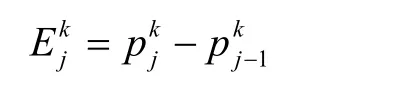
其中， αij≠ 0,1 = 1,2,3。通過計算可知，當

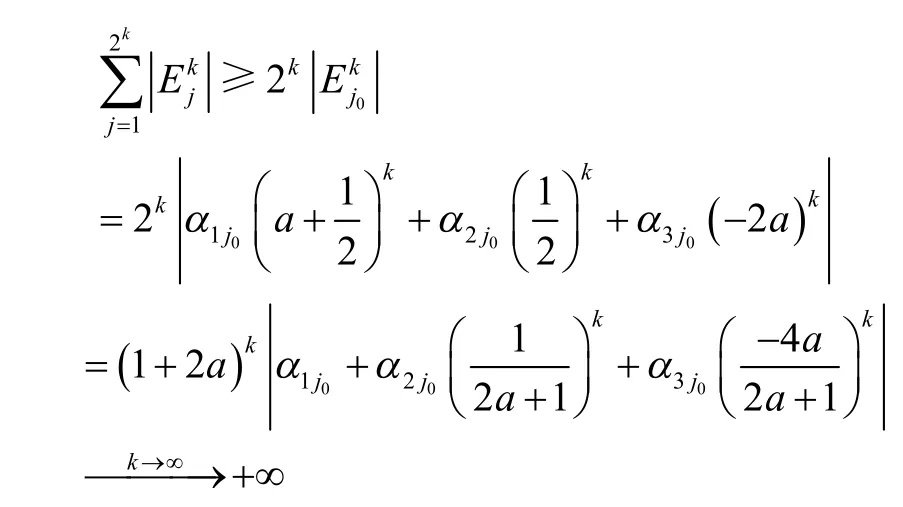
4 數值算例

下面給出關于3點binary插值細分格式性質的算例。

圖中的藍色實線表示初始控制多邊形，‘*’表示初始數據點，其他顏色的實線表示細分格式生成的極限曲線。

圖1 3點插值格式（綠線）與文獻[1]中的3點逼近格式（紅線）生成極限曲線的比較

圖2 細分參數a影響細分極限曲線

圖3中初始數據為 y-4= 16, y-3= 9, y-2=4, y-1= 1, y0= 0, y1= 1, y2= 4, y3= 9, y4= 16。品紅色實線表示 3點插值格式滿足保凸條件時細分八次的極限曲線；綠色實線表示細分格式不滿足保凸條件時細分八次的極限曲線。

圖3 細分格式滿足保凸條件和不滿足保凸條件

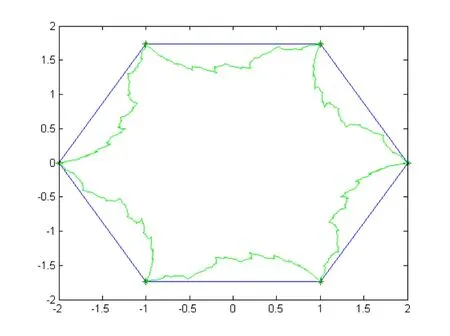
圖4 細分格式在a=時生成的分形曲線

從圖1中可以看出本文細分格式生成的插值細分曲線不具有幾何上的對稱性，但與逼近細分曲線比較起來具有保留初始數據的特點。從圖2和圖4可以看出細分曲線的形狀要受細分參數a的影響。而從圖3可以得出初始數據的性質和細分參數a共同決定細分格式的保凸性。

5 結 論

本文提出了一個3點binary插值細分格式，分析了該細分格式的連續性、保凸性以及分形等性質與細分參數之間的關系：

本文提出的細分格式為實際應用（如保凸性）以及快速生成分形曲線提供了一種方法。

[1] Siddiqi S S, Ahamd N. A new three point approximating C2subdivision scheme [J]. Applied Mathematics Letters, 2007, 20(6): 707-711.

[2] Siddiqi S S, Rehan K. Improved binary four point subdivision scheme and new corner cutting scheme [J]. Computers and Mathematics with Applications, 2010, 59(8): 2647-2657.

[3] Dyn N, Gregory J A, Levin D. A 4-point interpolatory subdivision scheme for curve design [J]. Computer Aided Geometric Design, 1987, 4(4): 257-268.

[4] Weissman A. A 6-point interpolatory subdivision scheme for curve design [D]. Tel-Aviv University, 1989.

[5] 蔡志杰. 變參數四點法的理論及其應用[J]. 數學年刊, 1995, 1(4) : 524-531.

[6] 丁友東, 華宣積. 一類非線性細分格式的保凸與分形性質[J]. 軟件學報, 2000, 11(9) : 1263-1267.

[7] Bahar S. Chaotic orbits and bifurcation from a fixed point generated by an iterated function system [J]. Chaos, Solitions & Fractals, 1995, 5(6): 1001-1006.

[8] Prusinkiewicz P, Lindenmayer A. The algorithmic beauty of plants [M]. New York: Springer-Verlag, 1990.

[9] 齊東旭, 戈建濤. 點解序列與分形構造 Ⅰ[ J]. 北方工業大學學報, 1993, 5(3): 1-13.

[10] Dyn N. Subdivision schemes in computer-aided geometric design. Advances in Numerical Analysis(Light W, ed.)[M]. Clarendon Press, 1992: 36-104.

[11] Cavaretta A S, Dahmen W, Micchelli C A. Stationary subdivision [J]. Memoirs of the American Mathematical Society, 1991, (93): 1-186.

Properties and Applications of a 3-point Binary Interpolatory Subdivision Scheme

Huang Shupei, Zheng Hongchan, Yan Feiyi, Hu Yun
(Department of Applied Mathematics, Northwestern Polytechnical University, Xian Shaanxi 710129, China)

In order to make the subdivision scheme which has good properties, such as continuity, preserving-convexity, a 3-point binary interpolatory subdivision scheme is proposed. Then, the relationship between the properties including continuity, preserving-convexity and fractal property and the parameter are analyzed. Finally, some applications are given about the properties of the subdivision scheme.

interpolatory subdivision schemes; continuity; preserving-convexity; fractal property

TP 391

A

2095-302X (2014)01-0031-06

2013-05-07；定稿日期：2013-05-21

國家自然科學基金資助項目（61070233）

黃樹培（1987-），男，河南許昌人，在讀碩士研究生。主要研究方向為計算機輔助幾何設計、計算機圖形學。E-mail：hsp_0906@163.com