Excel在非參數檢驗中的應用

何桂娟 黃守婷 楊建敏 王景偉 福建農林大學動物科學學院 福州 350002

Excel在非參數檢驗中的應用

何桂娟 黃守婷 楊建敏 王景偉 福建農林大學動物科學學院 福州 350002

本文以畜牧生產中兩個具體實例，介紹了符號秩和檢驗法與Mann-Whitney秩和檢驗法的相關原理及利用Excel電子表格進行檢驗的計算方法和操作步驟。該方法具有直觀、便捷和操作簡單等特點，在實際畜牧生產中有較大的實用性。

Excel配對樣本 非配對樣本 秩和檢驗

在畜牧生產過程中，許多資料總體分布類型未知，且樣本容量又較小，無法用參數統計法來解決，這時就可以采用非參數檢驗法（non-parametric test）。非參數檢驗在檢驗時不需利用總體參數（如平均數、標準差等）信息，主要利用樣本數據之間的差值比較及大小順序來檢驗數據資料是否來自同一個總體假設的檢驗方法，主要包括中位數檢驗、Wilcoxon符號秩和檢驗、Mann-Whitney秩和檢驗、Kruskal-Wallis檢驗等［1］。相對參數檢驗等方法，非參數檢驗對檢驗的限制較少，更能避免先見偏差；減少了應用中對假設條件的依賴，直觀性強，易于接受［2］。

與大型專業統計軟件如SAS和SPSS等相比較，Excel是一個統計功能豐富、操作方便、高效的統計軟件。Excel在畜牧生產中已廣泛運用于飼料配方優化計算，試驗數據記錄處理，繪制統計圖等。利用Excel實現非參數檢驗，主要是利用其公式與函數等功能，逐一實現理論算法的每一步驟，具有操作簡單，直觀易懂等特點。因此，以畜牧生產中兩個具體實例，介紹Excel的統計函數功能，實現樣本資料的秩和檢驗，為解決生產實際問題提供參考。

1 利用Excel實現配對樣本Wilcoxon符號秩和檢驗

1.1 配對樣本 Wilcoxon符號秩和檢驗原理Wilcoxon符號秩和檢驗在符號檢驗法的基礎上進一步考慮了差值絕對值的大小。絕對值的秩和能較明確地看出在數據的散布程度。設x1，x2，…xn，和y1，y2，…yn分別為來自總體X、Y的樣本，X、Y的分布函數分別為連續函數F1（x）和F2（x），建立假設：

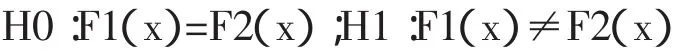
差值Zi=xi-y i（i=1，2，…n），取差值絕對值的秩，記為Ti。若Zi＞0，記其秩為Ti+，稱為正秩，若Zi＜0，記其秩為Ti-，稱為負秩。秩和絕對值較小者即為檢驗統計量T，再根據樣本容量數查符號秩和檢驗表得5%水平的顯著性臨界T0.05，當檢驗統計量T小于該臨界值時，就表明在這一顯著水平下可以否定原假設［3］。

1.2 實例分析

1.2 .1 數據來源 資料來源于某奶牛場利用兩種方法檢測10個奶樣的乳脂率（%）（表1）。

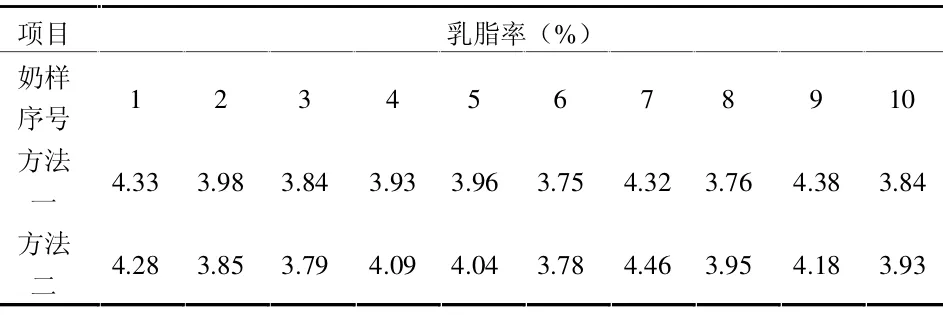
表1 兩種方法檢測的奶樣乳脂率

1.2 .2 數據輸入 打開Excel工作表，將數據輸入到電子表格（圖1）。

1.2 .3 分析步驟 根據輸入數據計算兩方法測定結果的差值，利用函數“ABS”得出各差值的絕對值，利用Excel排序功能，將絕對值的大小按從小到大順序排列，每一差值絕對值對應的順序號為該差值的秩次，若遇絕對值相同的情況則先求平均秩次，最后將秩次標上原差值符號，完成秩次的編輯（圖1）。

點中G2單元的空白框后，在“公式”菜單欄中選擇“插入函數”條目，點擊“SUMIF”分析工具，彈出函數參數對話框（圖2），點中表格秩次數據欄開始的F2單元，并拖動鼠標至F11單元，此時秩次數據自動進入變量區域，在“Criteria”選項中輸入“＞0”的條件，點擊“確定”按鈕，即求得正秩次和T+，輸入“＜0”的條件，則求得負秩次和T-（圖1）。

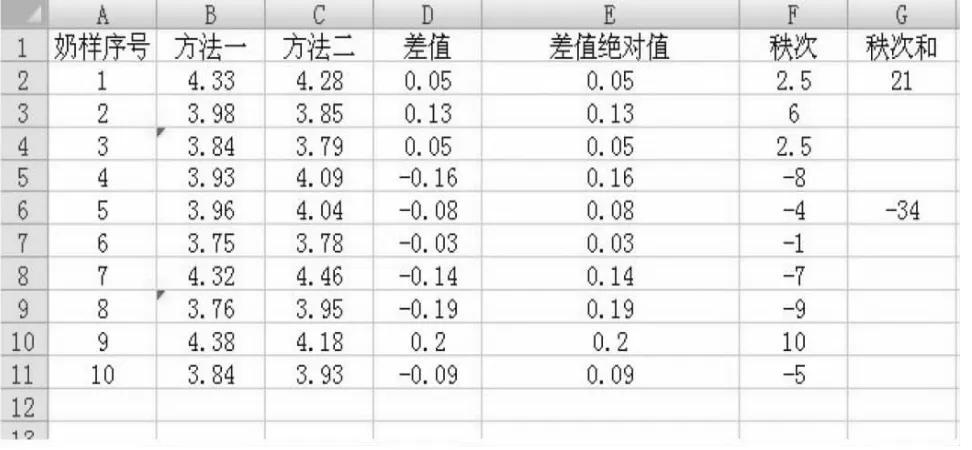
圖1 數據輸入格式及秩次和計算結果

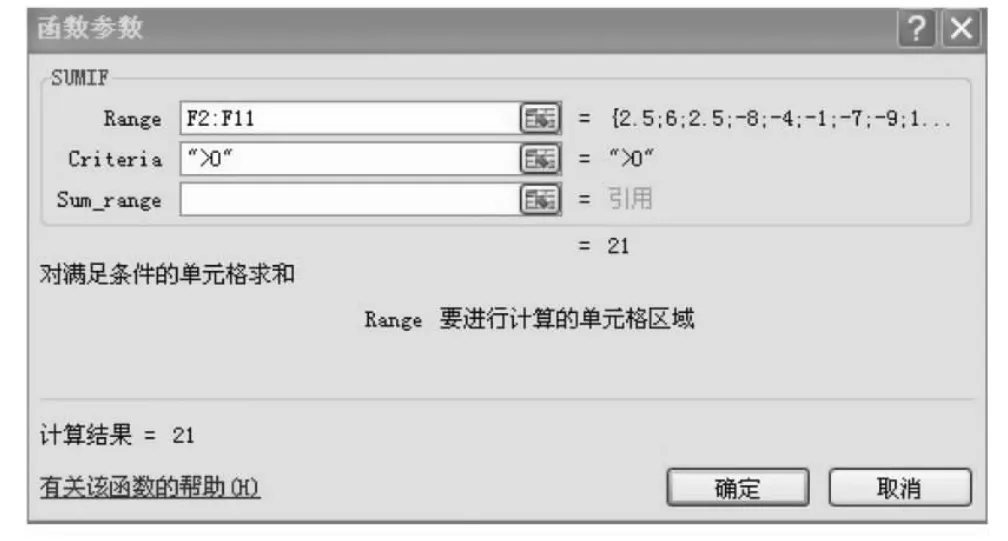
圖2 條件求和參數對話框

1.2 .4 結果分析 根據樣本含量對子數n（n=10），查符號秩和檢驗表，得顯著性水平為5%的臨界值為T0.05（10）=8。由圖1可知，秩和絕對值較小者為T+=21＞T，不能否定兩種檢測方法結果無差異的假設，表明兩種檢測方法結果在5%水平下差異不顯著。

2 利用Excel實現獨立樣本符號秩和檢驗

2.1 獨立樣本符號秩和檢驗法 獨立樣本秩和檢驗是抽自兩個獨立總體的兩個獨立樣本之間的比較，該檢驗法又稱為曼-惠特尼（Mann-Whitney）秩和檢驗。其基本原理是設兩個總體X和Y，它們的分布函數分別為F1（x）和F2（x），建立假設：

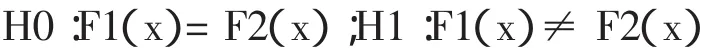
分別從這兩個總體X、Y抽取容量為n1、n2的樣本，n1+n2=n。計算取自總體X的樣本秩次和為T1，取自Y的秩次和為T2，抽樣較小的總體秩和即為檢驗統計量T值。如果兩個總體的分布沒有顯著性差異，則T值不會太大或太小，而是靠近最大值和最小值的中間，于是可以將T值作為秩和檢驗的統計量，當T的實際值超過臨界值時，就可以否定兩總體的分布沒有顯著性差異的原假設［2］。

2.2 實例分析

2.2 .1 數據來源 資料來源于某種禽公司孵化室對該公司2個養殖分場2012年1-8（9）月海蘭蛋雞的孵化率（表2）。

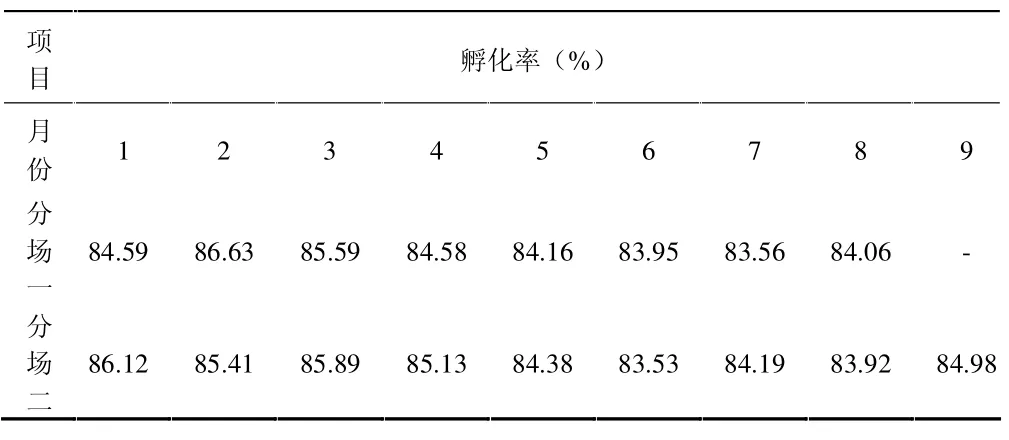
表2 海蘭蛋雞的孵化率

2.2 .2 數據輸入 打開Excel工作表，將數據輸入到電子表格（編號1-8為分場一的孵化率，編號9-17為分場二的孵化率）（圖3）。

2.2 .3 分析步驟 將兩組數據合并，按數值大小由小至大順序排列，數值最小的秩次為1，數值最大的秩次為兩組樣本容量之和，相同數值計算平均秩次（圖3）。點中D2單元區域的空白框，在“公式”菜單欄中選擇“插入函數”條目，點擊求和函數“SUM”，彈出求和函數參數對話框，點中電子表格該列數據開始的C2單元，并拖動鼠標至C9單元，此時秩次數據自動進入變量區域。點擊“確定”按鈕，即輸出計算結果。用同樣的方法求出分場二孵化率秩次和（圖3）。

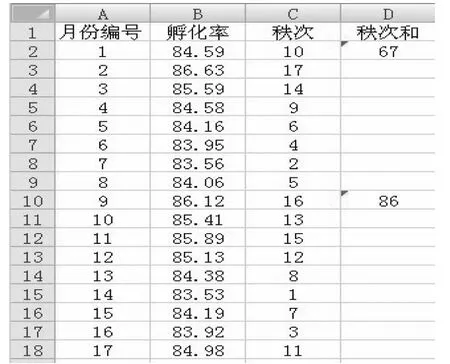
圖3 數據輸入格式及秩次和計算結果圖

2.2 .4 結果分析 根據樣本含量令較小一組為n1，樣本含量較大一組為n2，查非配對資料的秩和檢驗表可知，5%顯著水平的上限與下限兩個臨界值T1= 54，T2=90。由圖3可知，樣本含量較小組的秩和T= 67＜T2，不能拒絕兩總體分布沒有顯著性差異的原假設，即該公司兩分場海蘭蛋雞孵化率在5%水平下差異不顯著。

3 結論

通過以上兩個實例的分析發現，基于Excel的非參數檢驗方法，簡便實用，對于不太熟悉專業統計軟件的人員來說具有較強的實用性，在畜牧業生產及科研中有著重要的應用價值。

［1］ 謝莊.獸醫統計學［M］.北京：高等教育出版社，2005：107-110.

［2］ 袁加軍.統計基礎實驗［M］.廈門：廈門大學出版社，2010：119-129.

［3］ 張勤.生物統計學［M］.北京：中國農業大學出版社，2008：214-216.

A

1003-4331（2014）01-0021-02