Weighted Learning for Feedforward Neural Networks

Rong-Fang Xu, Thao-Tsen Chen, and Shie-Jue Lee

Weighted Learning for Feedforward Neural Networks

Rong-Fang Xu, Thao-Tsen Chen, and Shie-Jue Lee

—In this paper, we propose two weighted learning methods for the construction of single hidden layer feedforward neural networks. Both methods incorporate weighted least squares. Our idea is to allow the training instances nearer to the query to offer bigger contributions to the estimated output. By minimizing the weighted mean square error function, optimal networks can be obtained. The results of a number of experiments demonstrate the effectiveness of our proposed methods.

Index Terms—Extreme learning machine, hybrid learning, instance-based learning, weighted least squares.

1. Introduction

Neural networks have been becoming a powerful tool in many fields and disciplines. For example, in medical science, they can be used to recognize whether a person is suffering from cancer and help doctors to undertake subsequent diagnoses. In the financial field, they can be used to do stock forecasting or market analysis. In computer science, they can be used in speech recognition or image processing for identifying special objects or events.

There are many learning algorithms for training a multilayer perceptrons. In 1980s, a well-known algorithm called back propagation was proposed by Rumelhartet al.[1]. Since then, many methods have been proposed subsequently to accelerate the speed of convergence, such as the Levenberg-Marquardt back propagation[2], conjugate gradient[3], momentum term[1],[4], and adaptive step sizes[5].

Choet al. proposed a hybrid learning method[6]which combines gradient descent optimization and least squares for multilayer perceptrons. The weights connecting from the input layer to the hidden layer are optimized by gradient descent, while the weights connecting from the hidden layer to the output layer are optimized by least squares. Huanget al. proposed a very fast learning algorithm, called extreme learning machine (ELM)[7], for single hidden layer feedforward networks. The difference between Cho’s method and Huang's method is that the weights connecting from the input layer to the hidden layer are assigned random values in Huang’s method. Leeet al. proposed a neuro-fuzzy system with self-constructing rule generation and developed a hybrid learning algorithm consisting of a recursive singular value decomposition based least squares estimator and the gradient descent method[8].

For most aforementioned learning methods, training patterns are considered to be independent of the query which is the unknown input to be recognized. In other words, all training instances are of equal importance to the derivation of the weights involved in the neural networks. In 1990s, Ahaet al. proposed instance-based algorithms[9]. Its concept is that different training instances are of different degrees of importance to the query. If a training pattern is close to the query, it offers a large contribution. Otherwise, a small contribution is offered. Atkesonet al. surveyed some methods about locally weighted learning for regression problems and recognized positively the value of different contributions provided by different training instances to regression problems[10].

In this paper, we propose two weighted learning methods for the construction of single hidden layer feedforward neural networks. Both methods allow different contributions to be offered by different training instances. The first method, called weighted ELM (WELM), is an improvement on the extreme learning machine proposed by Huanget al.[7].The weights between the hidden layer and the output layer are optimized by weighted least squares. The second method, called weighted hybrid learning (WHL), applies back propagation to WELM and optimizes the weights between the input layer and the hidden layer. Our idea for both methods is to allow the training instances nearer to the query to offer bigger contributions to the estimated output. By minimizing the weighted mean square error function, optimal networks can be obtained. The results of a number of experiments demonstrate the effectiveness of our proposed methods.

The rest of this paper is organized as follows. Section 2 briefly introduces ELM. Section 3 presents WELM. In Section 4, we describe WHL which is another version of WELM. In Section 5, results of experiments are presented. Finally, concluding remarks are given in Section 6.

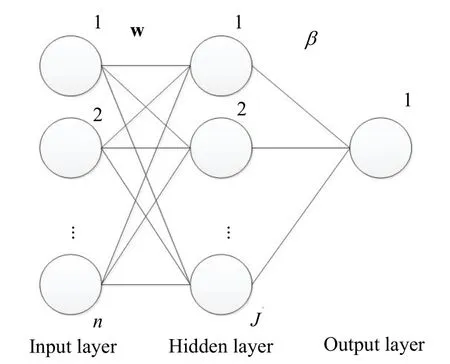
Fig. 1. Single hidden layer feedforward network.

2. ELM

ELM was introduced in [7]. Suppose a set ofNdistinct training instances (xi,ti),i=1, 2, …,N, are given, wherexiandtidenote the input and the desired output, respectively, of instancei, andsingle hidden layer feedforward network to do regression for this case is shown in Fig. 1, in which the first layer is the input layer, the second layer is the hidden layer, and the third layer is the output layer. The input layer hasnneurons, the hidden layer hasJneurons whereJis a number specified by the user, and the output layer has one neuron. Note thatnis the dimensionality of the input.

For any inputxi, the predicted output?iyis modeled as

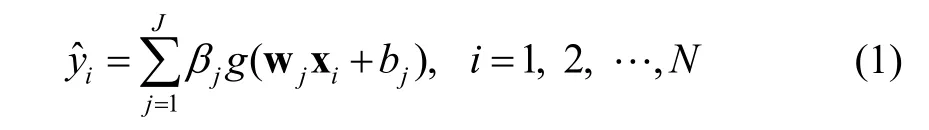
The weightswjand biasesbj,1jJ≤ ≤ , are set to randomly selected values. However, the weightsβj, 1jJ≤ ≤ , are learned from the training instances by minimizing the following summation:

which can be written as

where

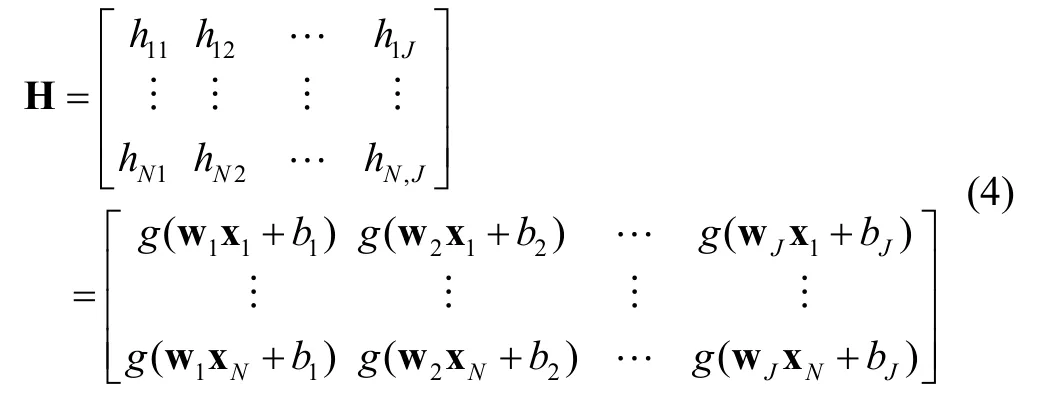
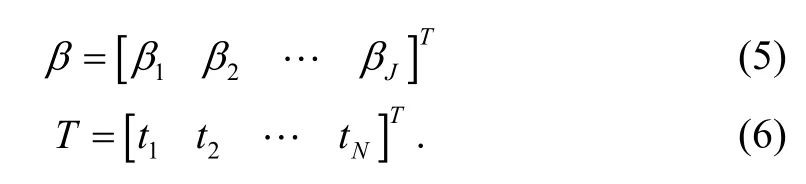
The least squares solution of (3) is

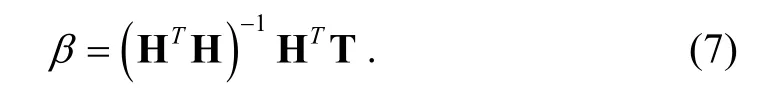
3. WELM

WELM is an improvement on ELM. As in ELM, the weights between the input layer and the hidden layer are set to randomly selected values. So are the biases of the hidden neurons. For ELM, the weights between the hidden layer and the output layer are optimized by least squares. For WELM, they are optimized by weighted least squares. Assume that we are givenq, called a query,q=[q1,q2, …,qn]T∈Rn, and we expect to derive the estimated output for the query. We compute the instance weightγifor theith training instance,i= 1, 2, …,N, by

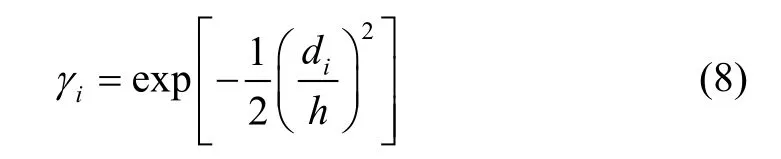
wherediis the distance between theith training instance and the query:

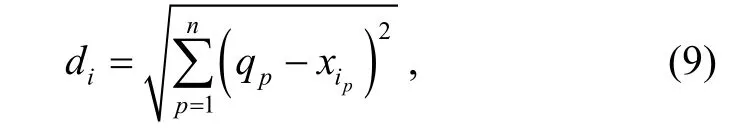
andhis a user-defined parameter, 0＜h≤1. Fig. 2 shows the relationship betweendiandγi. As it can be seen from this figure, when the training instance is closer to the query, the corresponding instance weight is bigger. On the contrary, when the training instance is farther away from the query, the corresponding instance weight is smaller.

Now we take the instance weights into account and (2) becomes

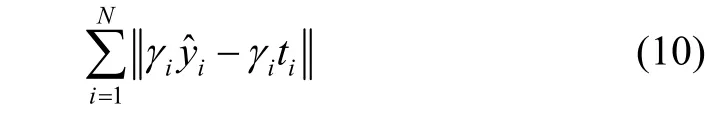
which can be written as

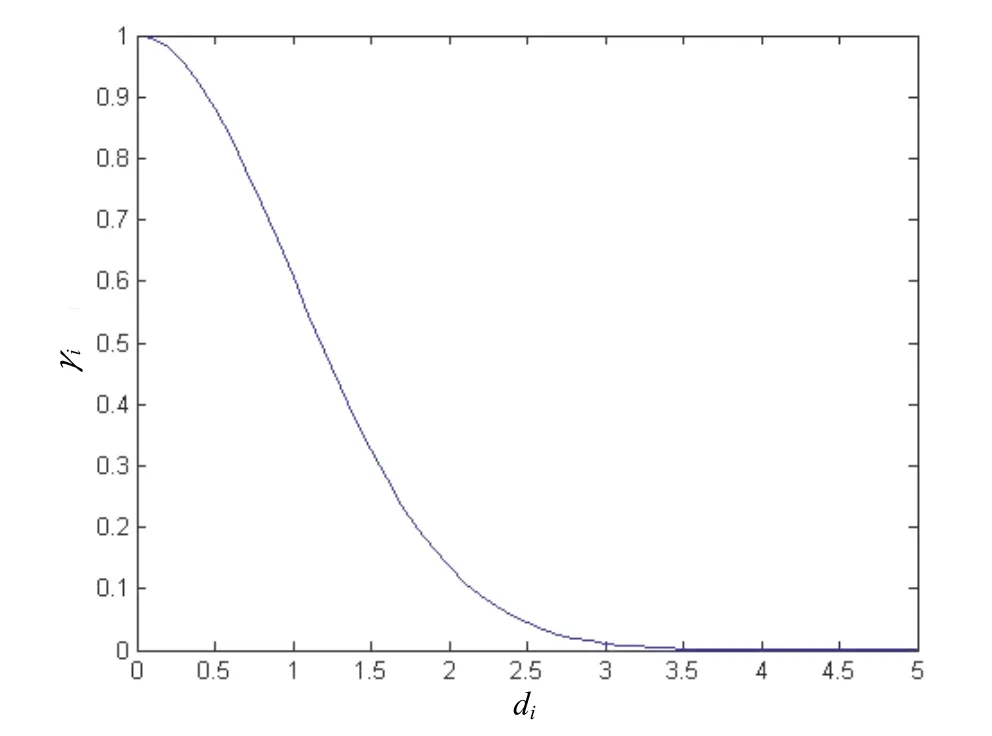
Fig. 2. Instance weight distribution.

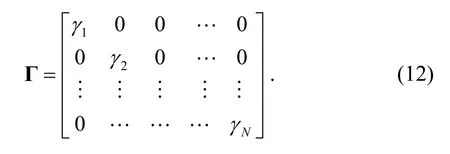
whereΓis the following diagonal matrix

The weighted least square solution of (11) is

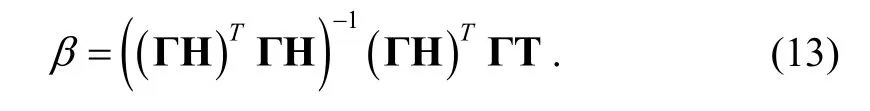
4. WHL

Weighted hybrid learning consists of gradient descent optimization and weighted least squares. The weights between the input layer and the hidden layer as well as the biases of the hidden neurons are updated by gradient descent[8]as follows:

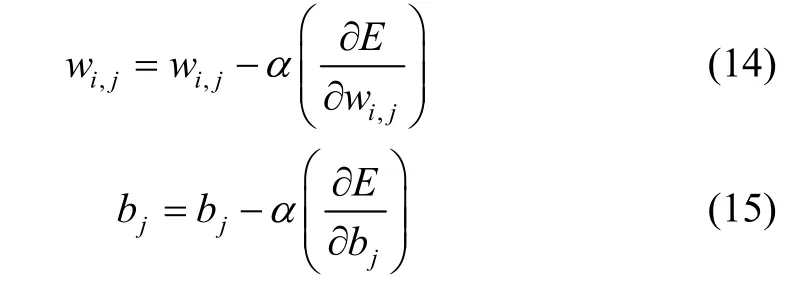
where

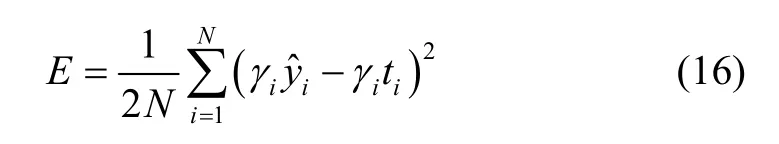
andαis the learning rate. Note that

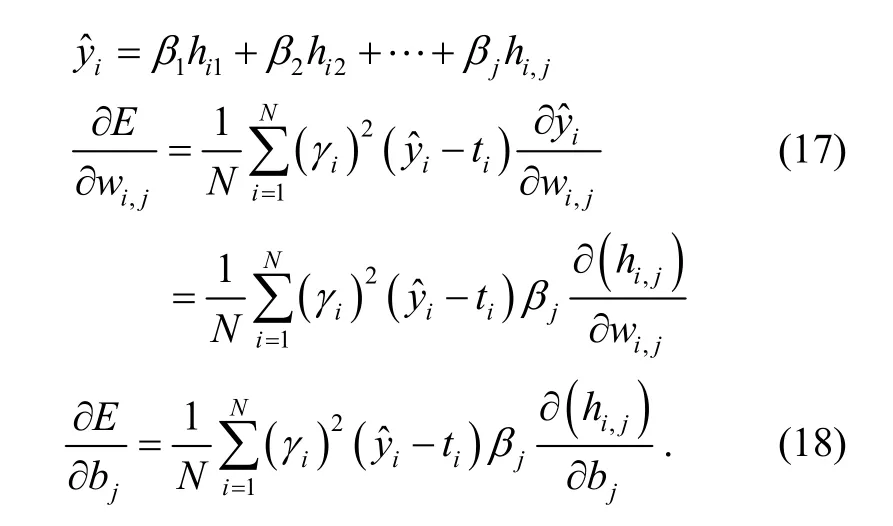
The whole process of weighted hybrid learning proceeds as follows. Random values are assigned to the weights between the input layer and the hidden layer. The biases of the hidden neurons are also assigned random values. First, the weights between the input layer and the hidden layer are kept constant. The biases of the hidden neurons are also kept constant. Then optimal values for the weights between the hidden layer and the output layer are obtained by weighted least squares. Next, the weights between the hidden layer and the output layer are kept constant. Then the weights between the input layer and the hidden layer, together with the biases of the hidden neurons, are updated by gradient descent. This process is iterated until the training error is acceptably small.

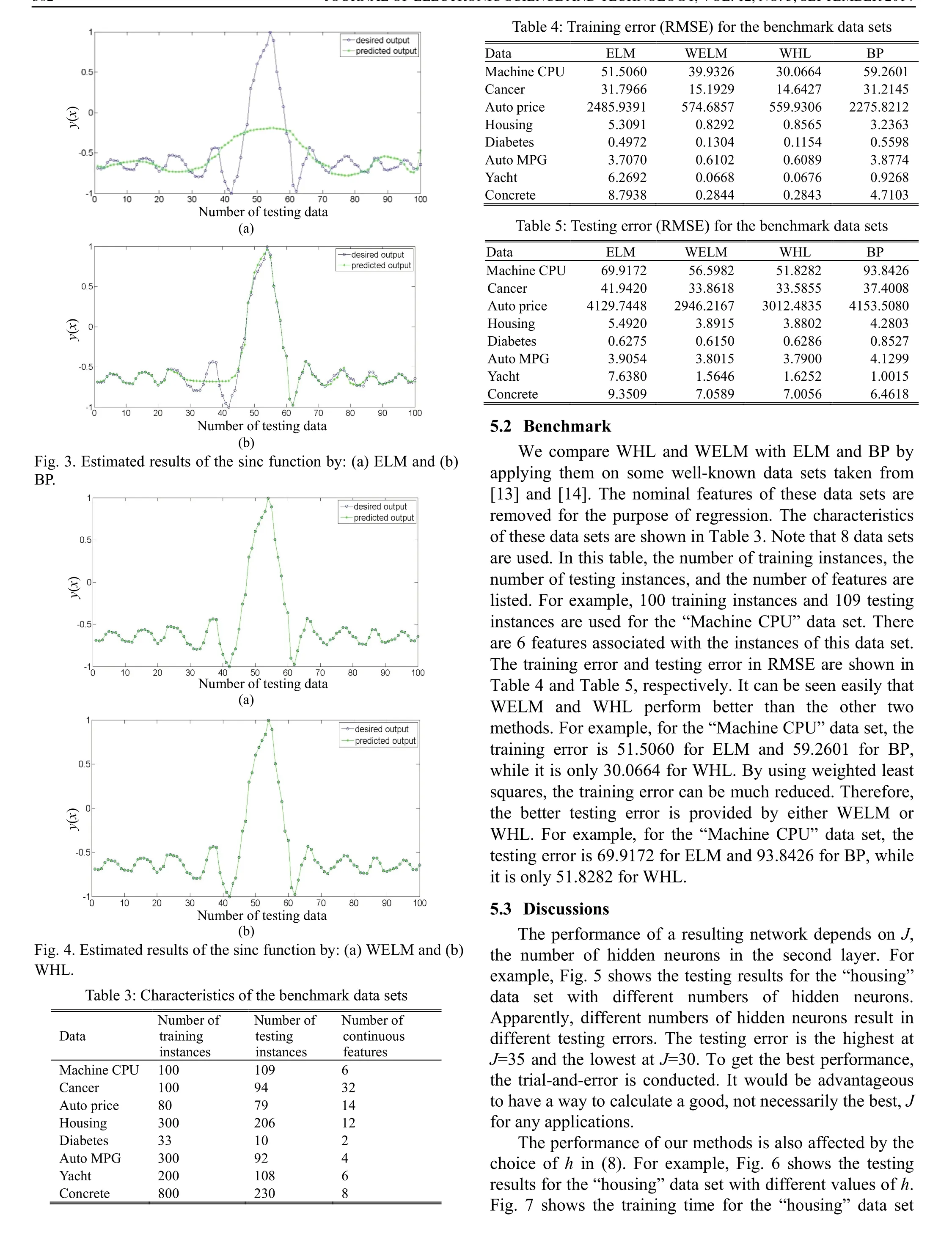
5. Experimental Results

We show the effectiveness of WELM and WHL in this section by presenting the results of experiments on some data sets. Comparisons with other methods, including ELM[11]and BP (Levenberg-Marquardt)[12], are also presented. In the following experiments, the features of all data sets are normalized to within the range of [0, 1] and the targets are normalized to within the range of [-1, 1]. The performance index adopted is the root mean square error (RMSE) defined as

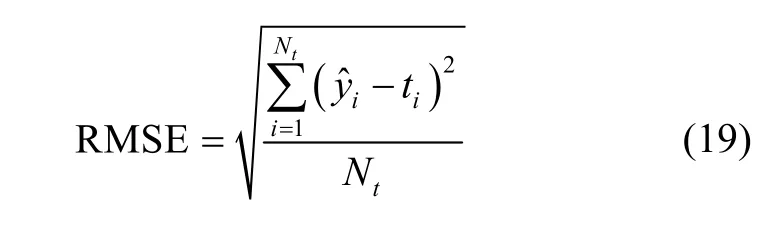
whereNtis the total number of instances involved, andtiand ?iyare the desired output and estimated output, respectively, of instancei. Note that for training RMSE,Ntis the number of training instances, and for testing RMSE,Ntis the number of testing instances. For each data set, ten-fold cross validation is used.

5.1 sinc

The sinc data used which is generated by the MATLAB function “sinc” can be represented as

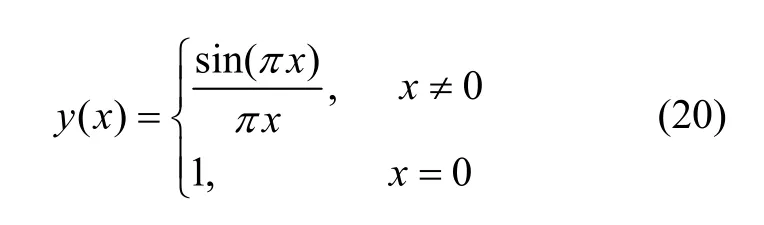
The range of the input is from -10 to 10. The number of training data is three hundred and one and the number of testing data is one hundred. The training error and testing error are shown in Table 1 and Table 2, respectively. Note that in these tables, “E-07” indicates “10-07”. Fig. 3 shows the estimated results obtained by ELM and BP, while Fig. 4 shows the estimated results obtained by WELM and WHL. It can be seen easily that WELM and WHL perform much better than the other two methods. For example, the training error is 0.1811 for ELM and 0.0179 for BP, while it is only 6.71E-07 for WHL. By using weighted least squares, the training error can be much reduced. Therefore, a nearly perfect match to the testing data is provided by either WELM or WHL. For example, the testing error is 0.1909 for ELM and 0.0182 for BP, while it is only 1.72E-05 for WHL.with different values ofh. Apparently, testing error decreases whenhis greater than 0.2. However, training time increases along withhclose to 1. From the above two figures, it can be seen that our methods perform well withhin the range of [0.2, 0.6].

Table 1: Training error for the sinc data set

Table 2: Testing error for the sinc data set

We have found that the approximation accuracy is considerably relevant to the relationship between training data and the query. Also, if there is a stronger relationship between a feature and the output, the weighted least squares method is more effective. Therefore, it is a good idea to use some preprocessing like feature selection or feature weighting to select highly relevant features before applying our weighted least squares methods.

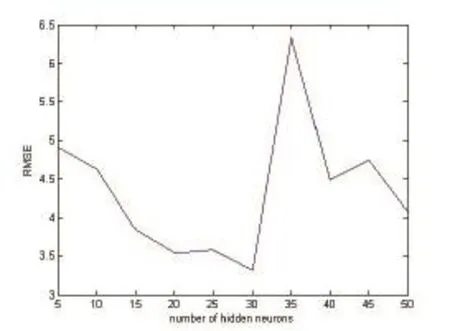
Fig. 5. Results for the housing data set with different numbers of hidden neurons.

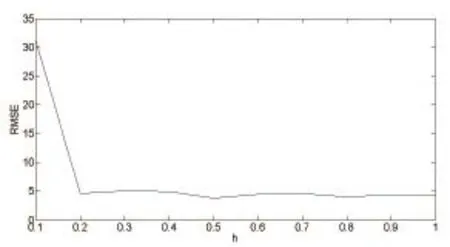
Fig. 6. Testing error for the housing data set with different h values.

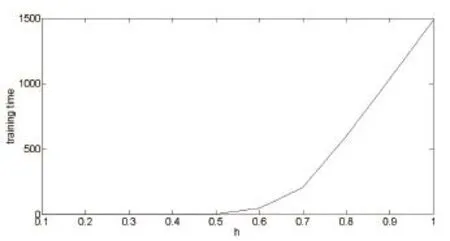
Fig. 7. Training time (sec) for the housing data set with different h values.

6. Conclusions

We have presented two methods, weighted extreme learning machine (WELM) and weighted hybrid learning (WHL), for single-hidden layer feedforward neural networks. Both methods allow different contributions to be offered by different training instances. WELM is an improvement on the extreme learning machine proposed by Huanget al.[7]. The weights between the hidden layer and the output layer are optimized by weighted least squares. On the other hand, WHL applies back propagation to optimize the weights between the input layer and the hidden layer of WELM. Our idea for both methods is to allow the training instances closer to the query to offer bigger contributions to the estimated output. By minimizing the weighted square error function, optimal networks can be obtained. The performance of both methods is shown to be better than ELM and BP by demonstrating the results of experiments on function approximation of several mathematical and real-world data sets.

[1] D. E. Rumelhart, G. E. Hinton, and R. J. Williams,“Learning representations by back-propagating errors,”Nature, vol. 323, pp. 533-536, Oct. 1986.

[2] M. T. Hagan and M. B. Menhaj, “Training feedforward networks with the Marquardt algorithm,” IEEE Tran. on Neural Networks, vol. 5, no. 6, pp. 989-993, 1994.

[3] C. Charalambous, “Conjugate gradient algorithm for efficient training of artificial neural networks,” IEE Proc. G, vol. 139, no. 3, pp. 301-310, 1992.

[4] T. P. Vogl, J. K. Mangis, A. K. Rigler, W. T. Zink, and D. L. Alkon, “Accelerating the convergence of the backpropagation method,” Biological Cybernetic, vol. 59, no. 4-5, pp. 257-263, 1988.

[5] R. A. Jacobs, “Increased rates of convergence through learning rateadaptation,” Neural Networks, vol. 1, no. 4, pp. 295-308, 1988.

[6] S.-Y. Cho and T. W. S. Chow, “Training multilayer neural networks using fast global learning algorithm—least-squares and penalized optimization methods,” Neurocomputing, vol. 25, no. 1-3, pp. 115-131, 1999.

[7] Q.-Y. Zhu, G.-B. Huang, and C.-K. Siew, “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1-3, pp. 489-501, 2006.

[8] S.-J. Lee and C.-S. Ouyang, “A neuro-fuzzy system modeling with self-constructing rule generation and hybrid SVD-based learning,” IEEE Trans. on Fuzzy Systems, vol. 11, no. 3, pp. 341-353, 2003.

[9] D. Kibler, D. W. Aha, and M. K. Albert, “Instance-based learning algorithms,” Machine Learning, vol. 6, no. 1, pp. 37-66, 1991.

[10] A. W. Moore, C. G. Atkeson, and S. Schaal, Lazy Learning, Norwell: Kluwer Academic Publishers, 1997.

[11] Source codes of ELM. [Online]. Available: http://www.ntu.edu.sg/home/egbhuang

[12] BP source codes in the MATLAB toolbox. [Online]. Available: http://www.mathworks.com/help/nnet/ug/trainand-apply- multilayer-neural-networks.html.

[13] UCI dataset. [Online]. Available: http://archive.ics.uci.edu/ml/

[14] Regression Datasets. [Online]. Available: http://www.dcc.fc. up.pt/ltorgo/Regression/DataSets.html

Rong-Fang Xuwas born in Tainan in 1990. He received the B.Sc. degree from National Kaohsiung University of Applied Sciences, Kaohsiung in 2012. He is currently pursuing the master degree with the Department of Electrical Engineering, National Sun Yat-Sen University. His current research interests include data mining and machine learning.

Thao-Tsen Chenwas born in Penghu in 1989. He received the B.Sc. degree in electrical engineering from Tamkang University, Taipei in 2011 and the M.Sc. degree in electrical engineering from National Sun Yat-Sen University, Kaohsiung in 2013. His research interests include data mining and machine learning.

Shie-Jue Leewas born in Kin-Men in 1955. He received the B.Sc. and M.Sc. degrees in electrical engineering from National Taiwan University, Taipei in 1977 and 1979, respectively, and the Ph.D. degree in computer science from the University of North Carolina, Chapel Hill in 1990. Dr. Lee joined the Faculty of the Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung in 1983, and has been a professor in the department since 1994. His current research interests include artificial intelligence, machine learning, data mining, information retrieval, and soft computing.

Prof. Lee was the recipient of the best paper award in several international conferences. The other awards won by him are the Distinguished Teachers Award of the Ministry of Education in 1993, the Distinguished Research Award in 1998, the Distinguished Teaching Award in 1993 and 2008, and the Distinguished Mentor Award in 2008, all from National Sun Yat-Sen University. He served as the program chair for several international conferences. He was the Director of the Southern Telecommunications Research Center, National Science Council, from 1998 to 1999, the Chair of the Department of Electrical Engineering, National Sun Yat-Sen University from 2000 to 2003, and the Deputy Dean of the Academic Affairs, National Sun Yat-Sen University from 2008 to 2011. He is now the Director of the NSYSU-III Research Center and the Vice President for Library and Information Services, National Sun Yat-Sen University.

Manuscript received December 7, 2013; revised March 10, 2014. This work was supported by the NSC under Grant No. NSC-100-2221-E-110-083-MY3 and NSC-101-2622-E-110-011-CC3, and also by “Aim for the Top University Plan” of the National Sun-Yat-Sen University and Ministry of Education.

R.-F. Xu and T.-T. Chen are with the Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung 80424 (e-mail: rfxu@water.ee.nsysu.edu.tw; ttchen@water.ee.nsysu.edu.tw).

S.-J. Lee is with the Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung 80424 (Corresponding author e-mail: leesj@mail.ee.nsysu.edu.tw).

Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.03.011