一類二部圖生成的廣義格子圖的鄰點可區(qū)別邊染色

劉信生，緱 艷，姚 兵，劉元元

（西北師范大學數(shù)學與統(tǒng)計學院，甘肅 蘭州730070）

1 預備知識

圖的染色問題是圖論的重要研究內容之一，具有重要的理論價值和實際意義.由不同實際問題引出了不同的染色概念，如倉庫數(shù)的研究、地圖染色、有線通信網、無線通信網等引出的鄰點可區(qū)別邊染色問題，得到國內外圖論研究者的關注.近些年來，雖然許多學者在這一領域已經取得了很多成果［1－8］，但這方面的研究工作尚屬開始，許多猜想的解決處于特殊圖的驗證階段.本文定義了一類2維廣義格子圖H2（G，n，m；k1，k2），且通過從圖的結構出發(fā)，利用構造染色的方法，得到了圖H2（Kp，p，n，m；p，p）的鄰點可區(qū)別邊色數(shù).從而驗證了鄰點可區(qū)別邊色數(shù)猜想.

定義1［1］設G（V，E）是階數(shù)至少為3的簡單連通圖，k－是正整數(shù).若G（V，E）是一個k－正常邊染色f 滿足：?uv∈E（G），S（u）≠S（v），其中S（u）＝｛f（uv）｜uv∈E（G）｝，則稱f 為G 的一個k－鄰點可區(qū)別邊染色，簡記為k－AVDPEC，且稱χ′a（G）＝min｛k｜G 存在k－AVDPEC｝為G 的鄰點可區(qū)別邊色數(shù).

猜想［1］設圖G 是階數(shù)至少為3的簡單連通圖，若G≠C5，則χ′a（G）≤Δ＋2.

定義2 把一個根圖G 做n 個拷貝，記做G（1），G（2），…，G（n）.連接每相鄰兩個G（i）與G（i＋1）（i＝1，2，…，n－1）間的k1對頂點，所得的圖記做H1（G，n；k1），并稱為1 維廣義格子圖，見圖1.然后把H1（G，n；k1）做m 個拷貝，記做H（1）1（G，n；k1），H（2）1（G，n；k1），…，H（m）1（G，n；k1）.將H（j）1（G，n；k1）中的每個根圖記為G（1，j），G（2，j），…，G（n，j）（j＝1，2，…，m）.連接G（i，j）與G（i，j＋1）（i＝1，2，…，n；j＝1，2，…，m－1）間的k2對頂點，所得的圖記做H2（G，n，m；k1，k2），并稱為2維廣義格子圖，見圖2.

注 定義2中的2維廣義格子圖不難推廣到t維廣義格子圖Ht（G，n1，n2，…，nt；k1，k2，…，kt）.

圖1 1維廣義格子圖H1（G，n；k1）

引理1［1］對階數(shù)不小于3的簡單連通圖G，有χ′a（G）≥Δ.若G 中存在相鄰的最大度點，則

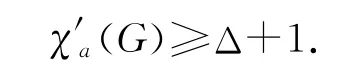
其他的相關術語和記號，可參見文獻［9］.

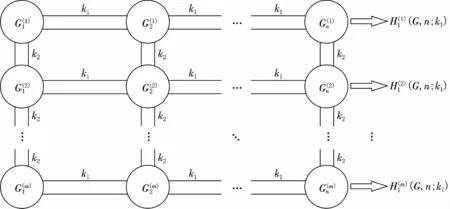
圖2 2維廣義格子圖H2（G，n，m；k1，k2）

2 主要結果

定理1 對n≥3，m≥3，有χ′a（H2（Kp，p，n，m；p，p））＝p＋6.

證明 把根圖Kp，p做n 個 拷 貝，記 做Kp（1，p），Kp（2，p），…，Kp（n，p）.且 記V（Kp（i，）p）＝Xi∪Yi，Xi∩Yi＝?，｜Xi｜＝｜Yi｜＝p，其 中Xi＝｛v1（i），v2（i），…，vp（i）｝，Yi＝｛u1（i），u2（i），…，up（i）｝（i＝1，2，…，n）.連 接vj（i）與vj（i＋1），uj（i）與uj（i＋1）（i＝1，2，…，n－1；j＝1，2，…，p）后所得的圖記做H1（Kp，p，n；p）.然后把H1（Kp，p，n；p）做m 個拷貝，記做H1（1）（Kp，p，n；p），H1（2）（Kp，p，n；p），…，H1（m）（Kp，p，n；p）.其中，H1（j）（Kp，p，n；p）中的每個根圖記為Kp（1，p，j），Kp（2，p，j），…，Kp（n，p，j）（j＝1，2，…，m）.且 記V（Kp（i，，pj））＝Xi，j∪Yi，j，Xi，j∩Yi，j＝?，｜Xi，j｜＝｜Yi，j｜＝p，其中Xi，j＝｛v1（i，j），v2（i，j），…，vp（i，j）｝，Yi，j＝｛u1（i，j），u2（i，j），…，up（i，j）｝（i＝1，2，…，n；j＝1，2，…，m）.連接vt（i，j）與vt（i，j＋1），ut（i，j）與ut（i，j＋1）（i＝1，2，…，n；j＝1，2，…，m－1；t＝1，2，…，p）后所得到的圖記做H2（Kp，p，n，m；p，p），見圖3.

圖3 2維廣義格子圖H2（Kp，p，n，m；p，p）

由于圖H2（Kp，p，n，m；p，p）中存在相鄰的最大度頂點，且Δ（H2（Kp，p，n，m；p，p））＝p＋4，由引理1可知，χ′a（H2（Kp，p，n，m；p，p））≥p＋5，如果χ′a（H2（Kp，p，n，m；p，p））＝p＋5，那么不失一般性，可設（在這里，我們用（u）表示S（u）在顏色構成的集合｛1，2，…，p＋6｝中的補集）.那么點vt（i，j）的所有鄰點的補集合里都必須包含色q.由于無論p是奇數(shù)還是偶數(shù)，由圖H2（Kp，p，n，m；p，p）的結構可知，這些點中的任意兩點之間都只有偶數(shù)條邊相連，故不存在這p＋4個點的完美匹配.因此，用p＋5種顏色不能對圖H2（Kp，p，n，m；p，p）進行鄰點可區(qū)別邊染色，故χ′a（H2（Kp，p，n，m；p，p））≥p＋6，為證χ′a（H2（Kp，p，n，m；p，p））＝p＋6，只需給出H2（Kp，p，n，m；p，p）的一個p＋6－AVDPEC即可.我們分兩種情況來證明結論.

情況Ⅰ 當p≡1（mod 2）時，分以下四個步驟給出具體染色f：

ⅰ 對拷貝H1（1）（Kp，p，n；p）的邊進行染色，令f 為：

當h≡1（mod 2）時，f（vi（h，1）uj（h，1））＝［j＋2（i－1）］p＋2（i＝1，2，…，p；j＝1，2，…，p；h＝1，2，…，n）.

當h≡0（mod 2）時，f（vi（h，1）uj（h，1））＝［j＋2（j－1）］p＋2（i＝1，2，…，p；j＝1，2，…，p；h＝1，2，…，n）.

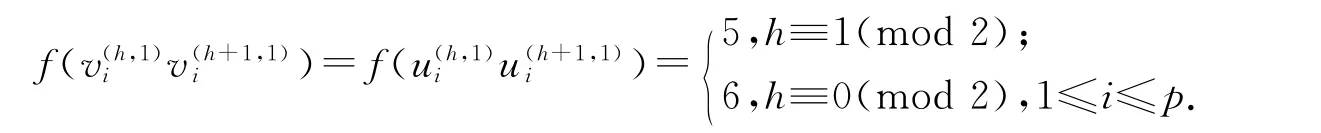
ⅱ 對拷貝H1（2）（Kp，p，n；p）的邊進行染色，令f 為：

當h≡1（mod 2）時，f（vi（h，1）uj（h，1））＝［j＋2（j－1）］p＋2（i＝1，2，…，p；j＝1，2，…，p；h＝1，2，…，n）.

當h≡0（mod 2）時，f（vi（h，1）uj（h，1））＝［j＋2（i－1）］p＋2（i＝1，2，…，p；j＝1，2，…，p；h＝1，2，…，n）.

ⅲ 拷貝H（j）1（Kp，p，n；p）（j≡1（mod 2）且3≤j≤m）的邊染色與H（1）1（Kp，p，n；p）的邊染色完全一致，拷貝H（j）1（Kp，p，n；p）（j≡0（mod 2）且4≤j≤m）的邊染色與H（2）1（Kp，p，n；p）的邊染色完全一致.

ⅳ 對每相鄰兩個拷貝H（j）1（Kp，p，n；p）與H（j＋1）1（Kp，p，n；p）（1≤j≤m－1）之間的邊進行染色，令f 為：

下證明以上染色是鄰點可區(qū)別的：

由圖H2（Kp，p，n，，m；p，p）的結構可知，只需證明中的各頂點是鄰點可區(qū)別的即可.因此，當i≡0（mod 2）且j≡0（mod 2）或當i≡1（mod 2）且j≡1（mod 2）時，對f 有當i≡0（mod 2）且j≡1（mod 2）或當i≡1（mod 2）且j≡0（mod 2）時，對f有

綜上，易看出當p≡1（mod 2）時，圖H2（Kp，p，n，m；p，p）中任意相鄰兩頂點的色集合均不同，故f是圖H2（Kp，p，n，m；p，p）的一個p＋6－AVDPEC.且滿足鄰點可區(qū)別邊色數(shù)猜想.

情況Ⅱ 當p≡0（mod 2）時，分以下四個步驟給出具體染色f：

ⅰ 對拷貝H（1）1（Kp，p，n；p）的邊進行染色，令f 為：

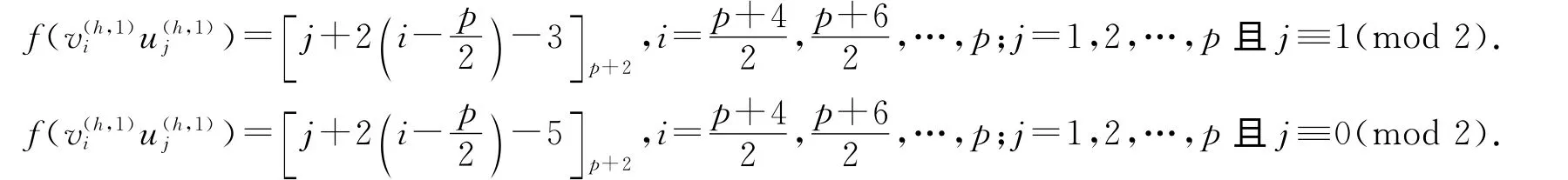
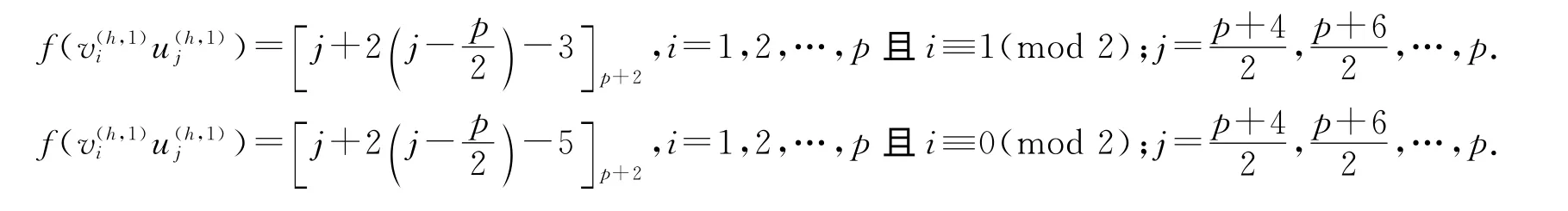
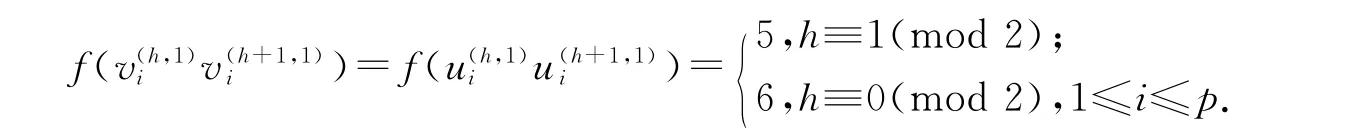
ⅱ 對拷貝H（2）1（Kp，p，n；p）的邊進行染色，令f 為：

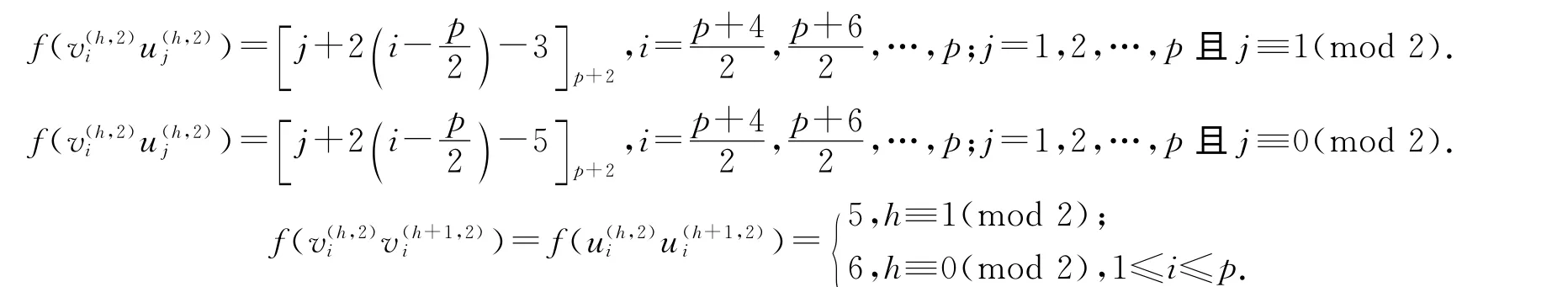
ⅲ 拷貝H（j）1（Kp，p，n；p）（j≡1（mod 2）且3≤j≤m）的邊染色與H（1）1（Kp，p，n；p）的邊染色完全一致，拷貝H（j）1（Kp，p，n；p）（j≡0（mod 2）且4≤j≤m）的邊染色與H（2）1（Kp，p，n；p）的邊染色完全一致.

ⅳ對每相鄰兩個拷貝H（j）1（Kp，p，n；p）與H（j＋1）1（Kp，p，n；p）（1≤j≤m－1）之間的邊進行染色，令f為:

下面證明以上染色是鄰點可區(qū)別的：

由圖H2（Kp，p，n，，m；p，p）的結構可知，只需證明中的各頂點是鄰點可區(qū)別的即可.因此，當i≡0（mod 2）且j≡0（mod 2）或當i≡1（mod 2）且j≡1（mod 2）時，對f 有且且6≤t≤p.當i≡0（mod 2）且j≡1（mod 2）或當i≡1（mod 2）且j≡0（mod 2）時，對f 有且0（mod 2）且

綜上，易看出當p≡0（mod 2）時，圖H2（Kp，p，n，m；p，p）中任意相鄰兩頂點的色集合均不同，故f是圖H2（Kp，p，n，m；p，p）的一個p＋6－AVDPEC，且滿足鄰點可區(qū)別邊色數(shù)猜想.