淺談概率論中“數(shù)學(xué)期望”概念的講解

曹小玲

（長江大學(xué) 信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023）

淺談概率論中“數(shù)學(xué)期望”概念的講解

曹小玲

（長江大學(xué) 信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023）

在概率論與數(shù)理統(tǒng)計的學(xué)習(xí)中，“數(shù)學(xué)期望”是一個比較抽象的概念，本文闡述了“數(shù)學(xué)期望”概念講解中比較重要的三個內(nèi)容，即：如何“定義”，如何“引申”到連續(xù)型隨機變量的定義，以及如何“過渡”到方差。

數(shù)學(xué)期望；概率論與數(shù)理統(tǒng)計；教學(xué)

在我們進行概率論與數(shù)理統(tǒng)計的教學(xué)中，教材的編排往往是在進行了隨機變量及其分布函數(shù)的學(xué)習(xí)之后，立刻進入隨機變量數(shù)字特征的學(xué)習(xí)，而最先面對的數(shù)字特征就是數(shù)學(xué)期望。“數(shù)學(xué)期望”這個概念的起源源于下面這個經(jīng)典典故。

早些時候，法國有兩個大數(shù)學(xué)家，一個叫做布萊士·帕斯卡，一個叫做費馬。帕斯卡認(rèn)識兩個賭徒，這兩個賭徒向他提出了一個問題。他們說，他倆下賭金之后，約定誰先贏滿5局，誰就獲得全部賭金。賭了半天，A贏了4局，B贏了3局，時間很晚了，他們都不想再賭下去了。那么，這個錢應(yīng)該怎么分？是不是把錢分成7份，贏了4局的就拿4份，贏了3局的就拿3份呢？或者，因為最早說的是滿5局，而誰也沒達到，所以就一人分一半呢？這兩種分法都不對。正確的答案是：贏了4局的拿這個錢的3/4，贏了3局的拿這個錢的1/4。這是為什么呢？假定他們倆再賭一局，A有1/2的可能贏得他的第5局，B有1/2的可能贏得他的第4局。若是A贏滿了5局，錢應(yīng)該全歸他；若B贏得他的第4局，則下一局中A、B贏得他們各自的第5局的可能性都是1/2。所以，如果必須贏滿5局的話，A贏得所有錢的可能為1/2+1/2× 1/2=3/4，當(dāng)然，B就應(yīng)該得1/4了。數(shù)學(xué)期望由此而來。

通過這幾年的教學(xué)體會和教學(xué)經(jīng)驗，筆者發(fā)現(xiàn)“數(shù)學(xué)期望”這一概念盡管來源于生活，而且跟現(xiàn)實生活結(jié)合得非常緊密，但因為它非常抽象，一般同學(xué)學(xué)到這個地方就會感覺到難于理解和接受。本文對數(shù)學(xué)期望概念的講解進行了介紹，以期起到“拋磚引玉”的作用。

一、關(guān)于如何定義“數(shù)學(xué)期望”

首先是如何引入的問題。對于如何引入“數(shù)學(xué)期望”，我們?yōu)榱藛酒饘W(xué)生的學(xué)習(xí)興趣，激發(fā)他們的學(xué)習(xí)動力，可以舉一些密切聯(lián)系生活的例子，比如上面的經(jīng)典典故，或者將上面的經(jīng)典典故作稍許變動，得到另外一個例子，如文獻[3]中就是將“賭金問題”換成了“乒乓球比賽問題”。我們也可以作這樣類似的變動，以吸引學(xué)生的課堂注意力，加深他們對《概率論與數(shù)理統(tǒng)計》這門課程在解決生活實際問題的作用是非常大的印象，喚起他們對這門課程的興趣，也激發(fā)他們對用數(shù)學(xué)方法處理現(xiàn)實問題的熱情。

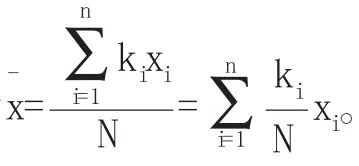
這種引入方法的特點是直接、簡單，節(jié)省上課時間，如果教師認(rèn)為教學(xué)任務(wù)比較繁重、教學(xué)時間比較緊張，無法保證后續(xù)內(nèi)容時間的把控，那么可以采用這種簡潔的方式進行引入工作。

由引例我們可以得到當(dāng)X是離散型隨機變量時，其數(shù)學(xué)期望的定義為：設(shè)離散型隨機變量X的分布律為：P{X=xk}=pk，k=1，2，…，n，如果級數(shù)絕對收斂，則稱級數(shù)為隨機變量X的數(shù)學(xué)期望（或均值），記為E（X）（在不產(chǎn)生混淆的情況下，也可記為EX），即

接著可通過一個例題來求解數(shù)學(xué)期望，從而加深學(xué)生對定義的理解和記憶。例如下面這則簡單例子：擲一枚六面骰子，已知其各面朝上的可能性是相同的，則擲得的點數(shù)的數(shù)學(xué)期望是多少呢？

此時可以引導(dǎo)學(xué)生思考：骰子的任何一面都不可能為3.5，然而最后算得的擲得的點數(shù)的數(shù)學(xué)期望卻是3.5，這說明了什么問題呢？這說明了期望值并不一定等同于常識中的“期望”，“期望值”也許與每一個結(jié)果都不相等。換句話說，期望值是該隨機變量取值的平均數(shù)，期望值并不一定包含于隨機變量的取值集合里，這就加深了學(xué)生對數(shù)學(xué)期望定義的理解和把握。

二、關(guān)于如何“引申”到連續(xù)型隨機變量期望的定義

對于連續(xù)型隨機變量其值充滿整個區(qū)間，且取每一特定值的概率均為0，因此不能直接利用上述離散型隨機變量期望定義求其數(shù)學(xué)期望。但可將連續(xù)型隨機變量離散化，再由離散型隨機變量的數(shù)學(xué)期望的定義引申出連續(xù)型隨機變量的數(shù)學(xué)期望的定義。

設(shè)連續(xù)型隨機變量為X，它的取值范圍可視為（-∞，+∞），把（-∞，+∞）劃分為無數(shù)個小區(qū)間，[x0，x1]，[x1，x2]，…，[xn-1，xn]，（n→∞），則X在其中任意一個小區(qū)間[xk-1，xk]中取值的概率近似為f（xk-1）Δxk-1，其中f（xk-1）是X的概率密度函數(shù)在xk-1的值（其實是在xk-1附近的值，可近似這樣認(rèn)為），Δxk-1=xk-xk-1。由離散型隨機變量期望的定義：X的數(shù)學(xué)期望就是X能取到的每個值乘以它取這個值的概率的積的和，即可引申得到連續(xù)型隨機變量的數(shù)學(xué)期望為：

由此得到連續(xù)型隨機變量數(shù)學(xué)期望的定義為：設(shè)連續(xù)型隨機變量X的概率密度函數(shù)為f（x），若積分xf（x）dx絕對收斂，則積分的值為隨機變量X的數(shù)學(xué)期望，記為E（X），即：

三、關(guān)于如何“過渡”到方差

因為方差本身就是一種數(shù)學(xué)期望，但是如何引出“方差”這一數(shù)學(xué)期望卻是要費一點心思的。比如說現(xiàn)在我們面前擺放著兩只手表，它們每日的走時誤差（以分為單位）分別以隨機變量和表示，其分布律如下。

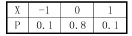
圖1 隨機變量X的分布律表

圖2 隨機變量Y的分布律表

從圖1、圖2中容易看出：E（X）=E（Y）=0，因此無法從期望評選出哪只手表質(zhì)量更優(yōu)。但直觀可看出：第一只手表的每日走時誤差X與其均值得偏離程度更小，走時更精確，質(zhì)量更好。此時可引導(dǎo)學(xué)生思考：我們應(yīng)該選擇什么樣的一個量來表示隨機變量與其均值的偏離程度呢？直接用X-E（X）顯然不太好，因為它有正負(fù)號差別，不便于比較大小。那么用好不好呢？它已經(jīng)避免了正負(fù)號的討論，顯然也不太好，因為它涉及到如何脫去絕對值的討論。此時我們可能想到用（X-E（X））2這個量比較好，因為它永遠(yuǎn)是非負(fù)的，便于比較大小，又不用考慮脫去絕對值的問題，但是我們又想到X的取值是隨機的，此時表示隨機變量與其均值的偏離程度應(yīng)該考慮X能夠取到的所有的點，而并非單一的一個點。那么怎么樣才能考慮到所有的點呢？此時我們可以回顧之前期望的定義，會發(fā)現(xiàn)期望正是考慮了隨機變量取值的所有的點的情況。因此，再在（X-E（X））2上加上期望符號就變成了，這就是用來表示隨機變量與其均值的偏離程度的量，我們稱它為方差，記為：，由此可得到方差的定義：設(shè)X是一個隨機變量，若存在，則E為X的方差，記為D（X）或Var（X），即：D

四、結(jié)語

通過實際的教學(xué)實踐，我們發(fā)現(xiàn)“數(shù)學(xué)期望”概念對于許多同學(xué)來說是非常抽象的，因此，對它概念的講解就應(yīng)該是我們必須注意的地方。本文是筆者對“數(shù)學(xué)期望”概念的講解的一點經(jīng)驗總結(jié)，希望能對概率論與數(shù)理統(tǒng)計的教學(xué)起到一點“拋磚引玉”的作用。

[1]盛驟，謝式千，潘承毅.概率論與數(shù)理統(tǒng)計[M].北京：高等教育出版社，2008.

[2]李正耀，周德強.大學(xué)數(shù)學(xué)——概率論與數(shù)理統(tǒng)計[M].北京：科學(xué)出社，2009.

[3]熊歐，仇海全，武潔.數(shù)學(xué)期望的教學(xué)方法新探[J].科技信息，2010，（3）.

G642.41

A

1674-9324（2014）45-0199-03

長江大學(xué)教研項目（JY2011023）

曹小玲（1981-），女，數(shù)學(xué)與應(yīng)用數(shù)學(xué)系，講師，現(xiàn)主要從事數(shù)字圖像處理和高等工程數(shù)學(xué)的教學(xué)與研究工作。