基于有限元強度折減法多級邊坡穩定性研究

陳寅春，胡文亮

(重慶市設計院，重慶 400015)

在我國西部交通事業的發展中，道路工程建設往往伴隨著高邊坡的出現。高邊坡在具有放坡條件的情況下多采用多級邊坡的形式，以提高邊坡穩定性。

20世紀末，有限元數值解法以其適用性強的優點在巖土工程領域廣泛應用，同時國內外多個研究采用有限元強度折減法求解均質土質邊坡的穩定系數，因其結果與傳統方法求解結果比較接近，逐漸得到學術界的認可。趙尚毅，等[1]采用有限元法不需做滑動面假設計算邊坡穩定性，其結果滿足應力應變關系，表明該分析方法的可靠性；韓愛民，等[2]采用強度折減法分析臺階寬度對邊坡破壞形式的影響；鄭穎人，等[3]采用強度折減法計算分析巖質邊坡和土質邊坡，并與傳統方法作對比，說明強度折減法的廣泛適用性；劉文治，等[4]對多級邊坡擋墻應力進行實驗測量，發現多級邊坡擋墻后水平推力有別于單級邊坡擋墻；周應華，等[5]分析認為多級邊坡平臺寬度達到一定值時，各級邊坡的相互影響較小，當某級邊坡產生局部失穩時不會導致其他級邊坡破壞。

鑒于目前多級邊坡在工程中應用較多而又缺少對其穩定性的系統研究，筆者采用有限元強度折減法分析邊坡級數、邊坡坡率及邊坡平臺寬度對多級邊坡穩定性的影響，為今后類似工程提供參考。

1 有限元強度折減法基本原理

1.1 強度折減法原理

強度折減法的原理就是不斷降低巖土強度指標直到邊坡數值計算達到失穩狀態[6]。以摩爾-庫倫材料屈服準則為例就是通過折減巖土材料強度參數(黏聚力c和內摩擦角φ)使結構處于臨界失穩破壞狀態。

選擇適應巖土材料屈服性質的摩爾庫倫屈服準則作為強度屈服準則，邊坡穩定性系數定義為沿滑動面的抗剪強度與滑動面上實際剪力的比值，如式(1)：

(1)

將式(1)兩邊同時除以F，得到式(2)：

(2)

式中：c為巖土的黏聚力，Pa；φ為巖土的內摩擦角，(°)；c′為巖土折減后的黏聚力，Pa；φ′為巖土折減后的內摩擦角，(°)；σ為正應力，Pa；τ為剪應力，Pa；l為受剪面積，m2。

令式(2)等于1，即巖土強度折減F倍后巖土達到臨界失穩的狀態。

1.2 臨界失穩狀態判斷依據

1)塑性區貫通法，即以某一幅值的廣義剪應變的貫通作為結構失穩標志，該方法不能準確地描述塑性區的發生與發展過程，并且廣義剪應變圖中設置的變化幅值大小會影響圖形中剪應變的顯示，使臨界狀態的標準定義具有模糊性[7]。

2)特征點位移法，繪制特征點在強度折減過程中的位移曲線，以該曲線出現較為明顯的轉折處作為判斷依據，此方法的難點在于特征點應選取在合適位置[8]。

3)計算不收斂法，有限元軟件計算過程中巖土結構失穩破壞時計算不收斂。迭代范圍、網格劃分及不平衡力系數等收斂條件會影響收斂性，但是在網格劃分規則的前提下收斂條件對穩定性系數的影響可以忽略[9]；若計算不收斂，則說明巖土結構某個區域產生無限大位移即失穩破壞。

以有限元迭代計算不收斂作為邊坡失穩破壞的判據依據標準更明確，更有說服力。

2 多級邊坡穩定因子分析

為了全面分析多級邊坡穩定性的影響因子對其穩定性的影響，分別建立每種因子的對比分析模型進行單因子研究。邊坡巖土材料參數：泊松比μ= 0.38，內摩擦角φ= 30°，彈性模量E= 1 300 MPa，重度γ= 22 kN/m3，黏聚力c= 20 MPa。

2.1 邊坡級數對邊坡穩定性的影響

邊坡級數分別取1，2，3級(圖1)，建立有限元模型，采用強度折減法計算，得到邊坡穩定性系數分別為1.238，1.288，1.363。可見，一定高度的邊坡放坡級數越多，其穩定性越好。

圖1 級數因子計算模型Fig.1 Calculation model of step factor

提取 3 種情況下多級邊坡臨界失穩狀態的最大剪應變云圖(圖2)。由圖2可見，3種情況下最大剪應變區有所變化，邊坡臨界失穩時最大剪應變區隨級數增多而增大。

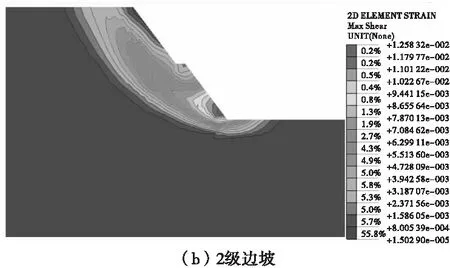
圖2 邊坡最大剪應變云圖Fig.2 The max shear strain map of slope

2.2 邊坡坡率對邊坡穩定性的影響

多級邊坡可有多種坡率，每一級坡率的改變對邊坡穩定性的影響均不相同，分別用a，b，c來表示(圖3)。建立有限元模型，采用強度折減法計算得到4種工況下多級邊坡穩定性系數(表1)。

圖3 坡率因子計算模型Fig.3 Calculation model of ratio factor

工況1234邊坡坡率a1∶0．751∶1．001∶0．751∶0．75b1∶0．751∶0．751∶1．001∶0．75c1∶0．751∶0．751∶0．751∶1．00穩定性系數1．3631．4631．4881．563

分析邊坡坡率因子可知，一定高度的邊坡，減小任意一級邊坡坡率都能一定程度提高邊坡穩定性。不同級的坡率對其穩定性的影響不同，計算結果表明，多級邊坡下部坡率變化對邊坡穩定性的影響比上部大。

提取各個工況下多級邊坡臨界失穩狀態的最大剪應變云圖，如圖4。由圖4可見，4種工況下最大剪應變區有所變化，邊坡臨界失穩時最大剪應變區隨邊坡坡率減小而增大，邊坡下部坡率變化對最大剪應變區影響較大。

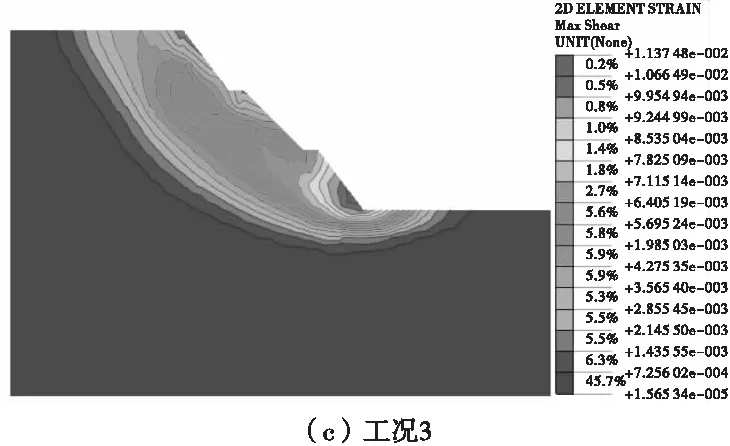
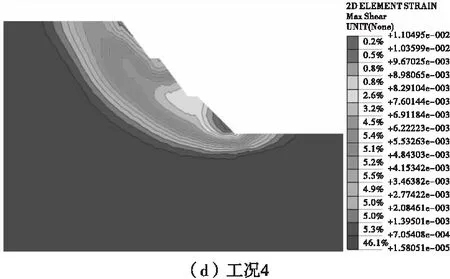
圖4 邊坡最大剪應變云圖Fig.4 The max shear strain map of slope

2.3 邊坡平臺對邊坡穩定性的影響

邊坡平臺是劃分邊坡級數的表現形式，同時也影響著多級邊坡穩定性。建立高度相同坡率相同平臺寬度不同的計算模型，每級平臺寬度分別用d，e來表示(圖5)。

圖5 平臺因子計算模型Fig.5 Calculation model of platform factor

建立有限元模型，采用強度折減法計算得到不同平臺寬度下多級邊坡穩定性系數(表2)。

表2 穩定性系數Table 2 Factor of safety

分析平臺寬度因子可知，一定高度的邊坡，平臺寬度增大能提高邊坡穩定性，增大相同平臺寬度，下部平臺對多級邊坡穩定性的影響比上部大。

提取各個工況下多級邊坡臨界失穩狀態的最大剪應變云圖(圖6)。可見，3種工況下最大剪應變區有所變化，邊坡臨界失穩時最大剪應變區隨平臺寬度增大而增大，邊坡下部平臺寬度對最大剪應變區影響較大。

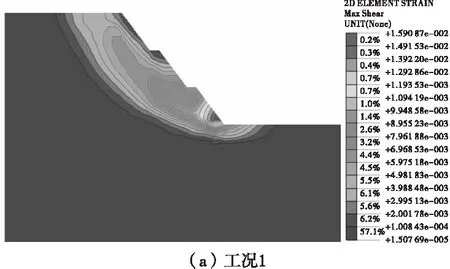
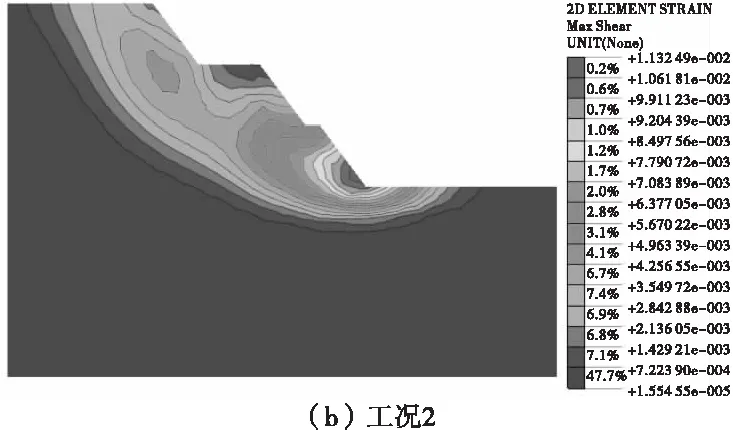
圖6 邊坡最大剪應變云圖Fig.6 The max shear strain map of slope

3 結 論

通過分析多級邊坡的級數、坡率及平臺寬度等因子對邊坡穩定性的影響，可以得到各種因子對多級邊坡穩定性的影響規律，得到結論如下：

1)高度一定的多級邊坡，在坡率及臺階寬度一定的情況下，邊坡級數越多，邊坡坡率越小，邊坡臺階寬度越大其穩定性越高。

2)多級邊坡的下部邊坡坡率對邊坡穩定性的影響比上部大；多級邊坡的下部邊坡平臺寬度對邊坡穩定性的影響比上部大。

3)邊坡受剪區域增大表現為邊坡穩定系數提高。邊坡受剪區域增大即邊坡更多土體參與抵抗邊坡滑動，提高了邊坡的抗滑力。

4)改變多級邊坡的級數、坡率及平臺寬度等工程措施提高邊坡穩定性的實質是增大邊坡臨界失穩時受剪區域而提高邊坡的抗滑力。

[1] 趙尚毅,鄭穎人,石衛民,等.用有限元強度折減法求邊坡穩定安全系數 [J].巖土工程學報,2002,24(3) :343-346.

Zhao Shangyi,Zhen Yingren,Shi Weimin,et al.Analysis on safety factor of slope by strength reduction FEM[J].Chinese Journal of Geotechnical Engineering,2002,24(3):343-346.

[2] 韓愛民,李建國,傅國利,等.基于有限差分強度折減法的多級邊坡破壞模式研究[J].工程地質學報,2007,15(6):784-788.

Han Ai’min,Li Jianguo,Fu Guoli,et al.Numerical analysis of failure modes in slopes with multi-steps using shear strengthen reduction FDM[J].Journal of Engineering Geology,2007,15 (6):784-788.

[3] 鄭穎人,趙尚毅.有限元強度折減法在土坡與巖坡中的應用[J].巖石力學與工程學報,2004,23(19):3381-3388.

Zheng Yingren,Zhao Shangyi.Application of strength reduction FEM in soil androck slope[J].Journal of Rock Mechanics and Engineering,2004,23(19):3381-3388.

[4] 劉文治,康小宏,王瑞,等.高填土邊坡多級擋土墻土壓力觀測試驗研究[J].云南農業大學學報,2010,25(3):424-431.

Liu Wenzhi,Kang Xiaohong,Wang Rui,et al.Observation experiment research on earth pressure of high filled soil slope multi-level retaining wall[J].Journal of Yunnan Agricultural University,2010,25(3):424-431.

[5] 周應華,周德培.均質邊坡分級開挖寬平臺設計初探[J].山地學報,2007,25(3):381-384.

Zhou Yinghua,Zhou Depei.Preliminary design of excavation platform for homogeneous slope[J].Journal of Mountain Science,2007,25(3):381-384.

[6] 徐干成.地下工程支護結構[M].北京:中國水利水電出版社,2001:3-5.

Xu Gancheng.The Underground Engineering Support Structure[M].Beijing:China Water Conservancy and Hydropower Press,2001:3-5.

[7] 魏海波,吳敏.邊坡的有限元分析及ANSYS軟件對邊坡開挖的模擬[J].東北水利水電,2004,20(4) :42-44.

Wei Haibo,Wu Min.Finite element analysis of side slope and side slope excavation simulated by ANSYS software[J].Water Resources & Hydropower of Northeast China,2004,20(4):42-44..

[8] 連鎮營,韓國城,孔憲京.強度折減有限元法研究開挖邊坡的穩定性[J].巖土工程學報,2001,23(4):407-409.

Lian Zhenying,Han Guocheng,Kong Xianjing.Stability analysis of excavation by strength reduction FEM[J].Chinese Journal of Geotechnical Engineering,2001,23 (4):407-409.

[9] 鄭穎人,肖強,葉海林,等.地震隧洞穩定性分析探討[J].巖石力學與工程學報,2010,29(6):1081-1088.

Zhen Yingren,Xiao Qiang,Ye Hailin,et al.Study of tunnel stability analysis with seismic load[J].Journal of Rock Mechanics and Engineering,2010,29(6):1081-1088.