稀疏度自適應的寬帶壓縮頻譜感知方法*
趙知勁,胡俊偉
(1.杭州電子科技大學通信工程學院 杭州310018;2.中國電子科技集團第36研究所通信系統信息控制技術國家級重點實驗室 嘉興314001)
1 引言
認知無線電(cognitive radio,CR)[1]允許次用戶(secondary user,SU)以機會式接入或共享方式動態利用主用戶(primary user,PU)空閑頻段,從而提高頻譜利用率,被認為是緩解頻譜短缺問題的有效方法。頻譜感知是認知無線電的關鍵技術之一,寬帶頻譜感知需要對低利用率的寬帶信號進行采樣,以奈奎斯特率采樣產生的數據量非常大,現有硬件水平很難滿足數據存儲和處理的要求。
壓縮感知(compressed sensing,CS)[2,3]理論允許稀疏信號以低于奈奎斯特速率的速率進行采樣,大大減輕了硬件的處理負擔。無線寬帶信號在頻域上具有天然的稀疏特性,因此壓縮感知在寬帶頻譜感知領域具有廣泛的應用前景。
[4]最先提出將壓縮感知技術應用于寬帶頻譜感知,參考文獻[5]在此基礎上,利用模擬信息轉換器(analog-to-information converter,AIC)對寬帶模擬信號進行欠采樣,這兩種方法均需要已知稀疏度。然而在實際寬帶頻譜感知中,信號頻譜的稀疏度通常是未知且動態變化的。參考文獻[6]在信號功率譜稀疏性未知的情況下,通過壓縮采樣和最小二乘重構出信號頻譜。參考文獻[7]通過少量測量值對稀疏度進行估計,并通過估計值盡可能減少采樣數目,但該方法需要通過兩個階段得到采樣信息,復雜度較高。本文首先提出一種基于分布式模型的稀疏度估計方法,通過匹配測試得到原子集合;然后根據約束等距性(restricted isometry property,RIP)條件[3],估計出信道稀疏度,并將此稀疏度作為支撐集重構的先驗信息;最后根據分布式系統中誤差的突發特性,引進頻點置信系數,改進支撐集選取和最終判決過程。本方法提高了稀疏度未知且信噪比較低時的頻譜感知性能。
2 基于分布式網絡的稀疏度估計方法
在稀疏度未知的情況下,很多算法都不能對信號進行精確重構,而稀疏度自適應匹配追蹤算法[8]采用較多迭代次數才能實現精確重構,其復雜度較高。參考文獻[9]以觀測矩陣滿足RIP條件為前提進行初步估計,然后通過與子空間追蹤(subspace pursuit,SP)算法相結合的迭代更新,估計出信號的稀疏度。此方法將稀疏度的更新放在SP迭代的內部,具有較高復雜度,且僅適用于SP算法。對此,本文提出了基于分布式模型的稀疏度估計方法。
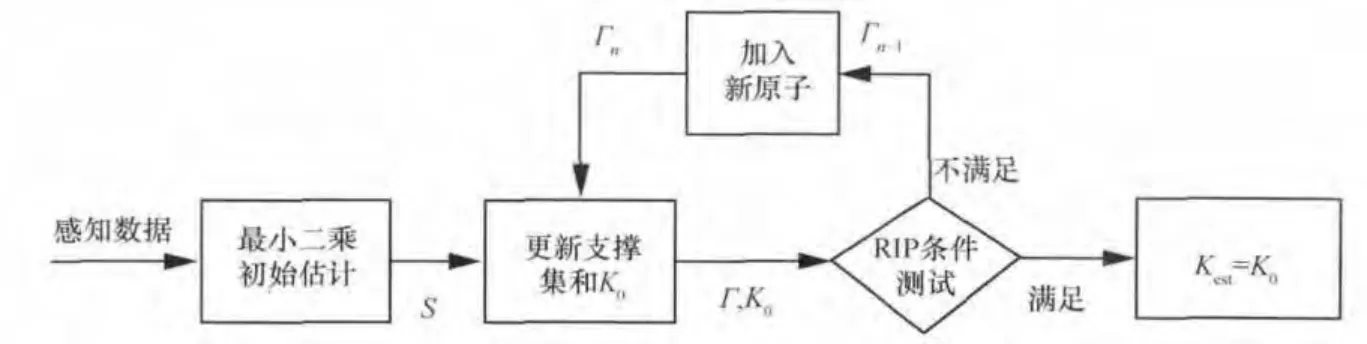
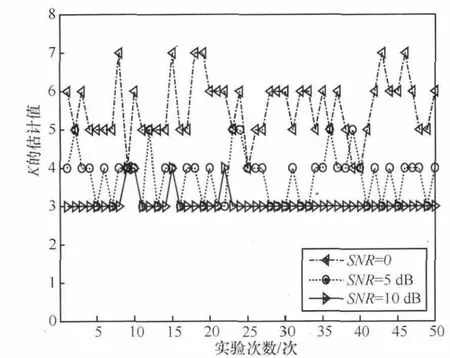
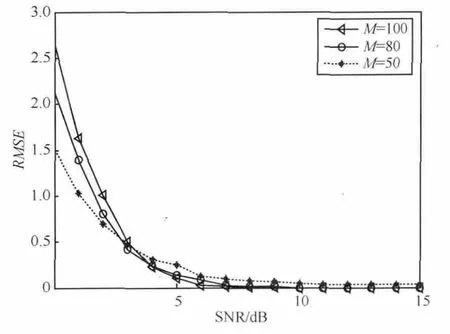
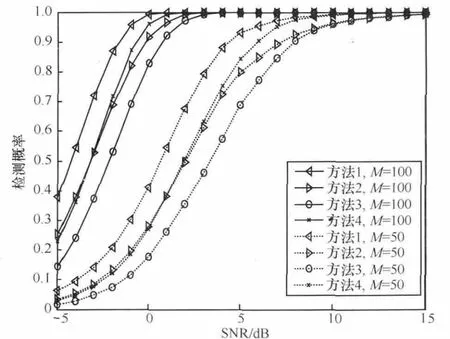
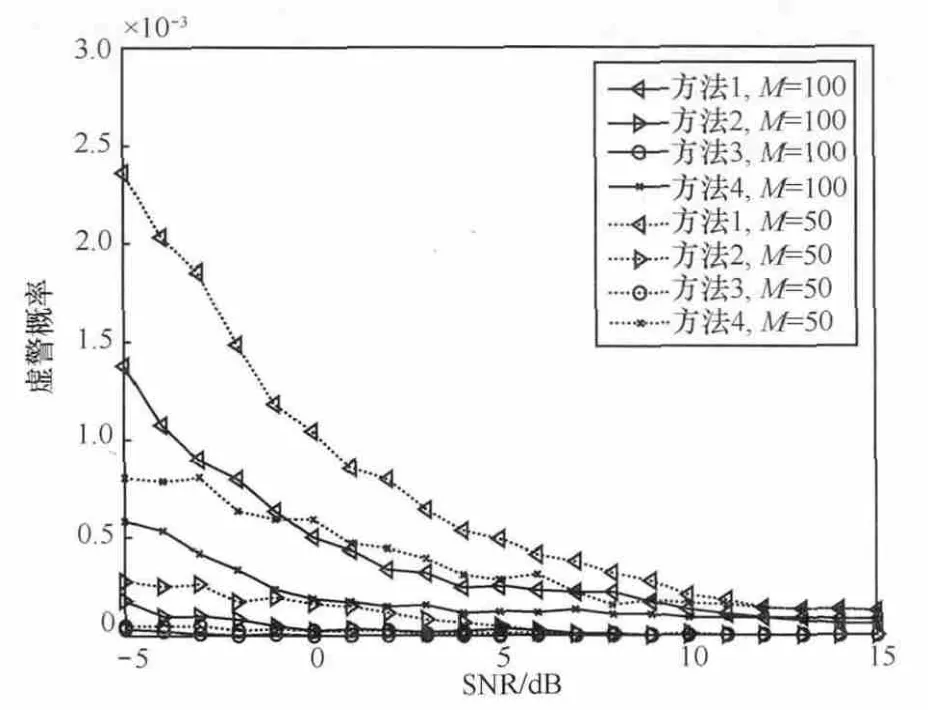
壓縮感知問題可以表示為:y=Φx。其中,x是N維的K稀疏信號,y是M維觀測向量(M< Candes E和Tao T在參考文獻[10]中給出了RIP的定義式,表示為: 若式(1)成立,則表示Φ滿足s階RIP性質,其中,δs∈(0,1)。 命題1[8]設Φ以參數(K,δK)滿足RIP性質,如果K0≥K,則: 其中,ΦΓ0為選取的原子所構成的支撐集矩陣,AT為A的轉置。反之,亦然。令: 根據參考文獻[11]的δK選擇理論取δK為定值。當滿足f(K0,Γ0)>g時,RIP條件成立,此時的K0即所估計的稀疏度值。基于此,本文的稀疏度估計方法如下。 本文考慮認知無線電網絡(CRN)中,頻譜帶寬為[0,Bmax],整個頻帶被劃分為C個信道,每個信道帶寬均為B,信道彼此互不重疊,融合節點已知信道的劃分,信道最大占用數Kmax已知。 分布式網絡中有J個SU同時進行頻譜感知,且彼此相互獨立,每個SU用戶通過AIC技術對寬帶模擬信號進行壓縮采樣,然后將感知信息發送給融合節點,融合節點對J個SU的數據進行融合,估計信道稀疏度Kest。 因為J個SU感知數據均是對同一個信號源的感知,它們所感知到的頻譜占用情況相同,即其支撐集是相同的,因此融合節點采用基于JSM-2的分布式壓縮感知(distributed compressive sensing,DCS)[12,13]。其感知模型為: 其中,xj為第j個SU的采樣數據,yj為第j個SU的感知數據,Sj為xj在傅里葉域的稀疏表示,Φj為各個SU的歸一化觀測矩陣,Ψ為傅里葉基。令: 其中,X∈RJN,Y∈RJM,Φ∈RJM×JN,因此融合節點數據可以表示為Y=ΦX=ΦΨS=ΘS,S為X在傅里葉域的稀疏表示。令: 初始化選取支撐集Γ0表示為: 其中,hi為h的第i個分量,β∈(0,1]為匹配系數,且令Γ0中元素的個數為K0。當β取適當值時,初始化選擇多個匹配度較高的原子,減少后續更新次數,使算法更加高效,一般選取β為0.7~0.9。 頻譜感知注重的是準確、快速地檢測出寬帶頻譜中的空洞,以便SU能夠及時接入空閑信道,而無需對頻譜進行精確重構,只需恢復出頻譜支撐集,因此本文提出一種寬支撐集的分布式頻譜感知方法。 因為由第2節的稀疏度估計方法得到的稀疏度Kest會存在誤差,因此本文擴大候選支撐集,利用各感知節點的分集效應,由于某一頻點在多個SU中同時發生錯誤的概率極低,因此通過置信系數更新可有效地刪除由于隨機誤差而錯選的支撐集[14],以提高支撐集選取的準確率,也就是提高稀疏度估計精度。 以第2節估計的Kest作為已知的稀疏度先驗信息,在融合中心對第j個SU數據通過OMP算法迭代2Kest次得到重構信號的支撐集,記為Locj,稱為寬支撐集。寬支撐集具有一定冗余信息,利用冗余信息可增加支撐集選取成功率。 每個信道中采樣p個頻點,總頻點數為N=C×p。令Q為非零頻點集合,Ω為頻點的全集,Qc為Q關于全集的補集,Δ為置信系數更新步長,Pth為系數閾值。假設第i個頻點置信系數為Pi,將Pi初始化為定值Pi=P。對第j個SU節點數據進行頻點置信系數判決。若第i個頻點在Locj中,則Pi=Pi+Δ;否則,Pi=Pi。當Pi≥Pth(Pth為門限值)時,則選中此頻點并在Q中標記第i個頻點。完成J個SU節點的N個頻點置信系數判決后,將補集Qc=Ω-Q中的頻點系數置零;計算每個信道的能量,能量最大的前Kest個非零信道即活躍信道,若非零信道個數小于Kest,則只取非零的信道標記為活躍信道,d表示系統判決的活躍信道集合,非活躍信道即頻譜空洞。 基于稀疏度估計的寬頻譜支撐集感知算法主要步驟如下。 輸入:M維觀測向 量yj(j=1,2,…,J),SU節點數為J,信道最高占用數Kmax,觀測矩陣Φj(j=1,2,…,J),更新步長Δ,閾值Pth,為Θj的第i列,Ω={k|1≤k≤N}。 輸出:活躍信道集合d。 (3)若f (4)若K0>Kmax,則Kest=Kmax,否則Kest=K0。tmax=2Kest,j=1;t=1。 (6)若t (7)對每個頻點i進行置信系數判決,若i∈Locj,則Pi=Pi+Δ,j=j+1。 (8)若j (9)Qc=Ω-Q,對Qc中所有頻點的系數置零。計算所有信道能量,為第j個SU的第c個信道能量,則活躍信道為d={i/Ec前Kest個最大的非零值}。 本節驗證本文稀疏度估計算法的效果。由式(4)可知,g是關于δK的單調遞減函數,為了保證后續信道漏檢概率維持在較低水平,因此本文提出的稀疏度估計方法要求估計的稀疏度不小于實際稀疏度,所以選取較小的δK=0.05。取M=100,N=256,隨機產生[1,32]內的K個整數表示活躍信道數,疊加噪聲為高斯白噪聲。用均方根誤差(RMSE)(如式(9)所示)分析稀疏度估計性能。其中L為實驗次數,Kest(l)為第l次實驗估計的稀疏度值,K(l)為第l次實驗實際稀疏度值。 圖1 稀疏度估計流程 K=3、L=50時,不同信噪比下稀疏度估計曲線如圖2所示。由圖可見,信噪比越低,稀疏度估計性能越差,越容易出現過估計。當信噪比為10 dB時,能以較大概率估計出稀疏度值。圖3給出M=50、80和100時稀疏度估計的均方根誤差。由圖可見,隨著信噪比增大,均方根誤差逐漸降低;當信噪比大于3 dB時,隨著采樣點數增大,均方根誤差減小;而當信噪比低于3 dB時,因為信號本身稀疏結構破壞較嚴重,導致稀疏度均方根誤差值并不隨著采樣點數增加而降低,但這并不影響系統的性能,可以通過置信系數的方法消除過估計的影響。 圖2 不同信噪比下K的估計曲線 圖3 稀疏度估計的均方誤差 在本節仿真中,以估計的信道稀疏度作為仿真的先驗條件;假設頻譜帶寬為0~64 MHz,信道數目C=32,每個信道帶寬為2 MHz;隨機生成K個[1,32]的整數表示活躍信道,記為集合k,k(i)表示集合中的第i個元素(1≤i≤K);假設每個信道主用戶具有相同功率W=1,疊加的噪聲為高斯白噪聲;選取K=3,J=5,Kmax=6,p=8。在不同信噪比下進行T=10 000次蒙特卡洛仿真。本文采用如式(10)和式(11)所示的檢測概率Pd和虛警概率Pf分析頻譜感知算法性能。 其中,kc表示非活躍信道。Num(k(i)∈d|k(i)∈k)表示活躍信道集合k與估計的活躍信道d中相同元素的個數;Num(kc(i)∈d|kc(i)∈kc)表示活躍信道集合的補集kc與估計的d中相同元素的個數。 本節分析比較4種算法的性能,方法1是本文提出的稀疏度自適應的寬頻譜支撐集頻譜感知算法,方法2是稀疏度自適應的同步正交匹配追蹤算法,方法3為稀疏度已知的同步正交匹配追蹤算法[13],方法4是稀疏度已知的寬支撐集算法。圖4和圖5給出了不同信噪比下,M取不同值時4種算法的頻譜檢測概率和虛警概率。由圖可知,M相同時,本文算法性能最優。當M=100,信噪比大于0時,本文算法的檢測概率達到100%;信噪比為-5~-1 dB時,本文方法的檢測概率比方法2和方法4高0.1,比方法3高0.2;當M=50時,信噪比大于10 dB時,本文算法的檢測概率達到100%;信噪比為-1~6 dB時,本文方法的檢測概率比方法2和方法4高0.1,比方法3高0.2。同時由圖5可見,隨著信噪比的提高,4種方法的虛警概率都降低;本文方法的虛警概率比其他3種方法大,但僅增大10-3量級。在實際頻譜感知中,首先要保證主用戶可靠通信。活躍信道的檢測概率高可以保證主用戶通信,虛警概率增大不影響主用戶通信,而僅降低空閑信道被SU利用率,因此適度地增大虛警概率是可以接受的。 圖4 不同信噪比下信道檢測概率 圖5 不同信噪比下信道虛警概率 針對實際系統中信道稀疏度是未知且時變的特點,本文提出了稀疏度自適應的頻譜感知方法。該方法首先基于分布式網絡估計稀疏度初值,然后通過置信系數迭代更新稀疏度,估計得到的稀疏度即為頻譜支撐集,也就實現了頻譜感知。仿真結果表明,在低信噪比條件下本方法的頻譜感知性能優于已知稀疏度的頻譜感知方法,本算法是一種實用的寬帶頻譜感知算法。 參考文獻 1 Mitola J.Cognitive radio:an integrated agent architecture for software defined radio.Stockhdm:Royal Institute of Technology,2000 2 Donoho D L.Compressed sensing.IEEE Transactions on Information Theory,2006,52(4):1289~1306 3 Candes E,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information.IEEE Transactions on Information Theory,2006,52(2):489~509 4 Zhi T,Giannakis G B.Compressed sensing for wideband cognitive radios.Proceedings of IEEE International Conference on Speech and Signal Processing,Honolulu,HI,USA,2007:1357~1360 5 Polo Y L,Ying W,Pandharipande A,et al.Compressive wide-band spectrum sensing.Proceedings of IEEE International Conference on Speech and Signal Processing,Taipei,China,2009:1655~1667 6 Leus G,Ariananda D D.Power spectrum blind sampling.IEEE Signal Processing Letters,2011,18(8):443~446 7 Wang Y,Tian Z,Feng C Y.Sparsity order estimation and its application in compressive spectrum sensing for cognitive radios.IEEE Transactions on Wireless Communications,2012,11(6):2116~2125 8 楊成,馮巍,馮輝等.一種壓縮采樣中的稀疏度自適應子空間追蹤算法.電子學報,2010,38(4):1914~1917 9 Candes E J,Tao T.Decoding by linear programming.IEEE Transactions on Information Theory,2005,51(12):4203~4215 10 Candes E J,Tao T.Stable signal recovery from incomplete and inaccurate measurements.Communications on Pure and Applied Mathematics,2006,59(8):1207~1223 11 Lu Y,Guo W B,Wang X,et al.Probabilistic greedy pursuit for streaming compressed spectrum sensing.The Journal of China Universities of Posts and Telecommunications,2011,18(5):15~21 12 Baron D,Wakin M B,Duarte M.Distributed Compressive Sensing.Technical Report,Rice University,2006 13 Tropp J A,Gilbert A C,Strauss M J.Simultaneous sparse approximation via greedy pursuit.Proceedings of IEEE International Conference on Acoustics,Speech,and Signal Processing,Philadelphia,2005:721~724 14 Do T T,Lu G,Nguyen N,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing.Proceedings of Asilomar Conference on Signals,System,and Computers,Pacific Grove,California,2008:581~587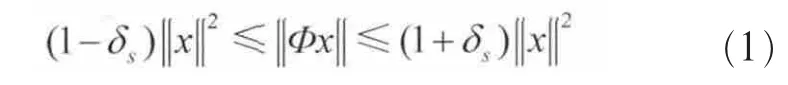
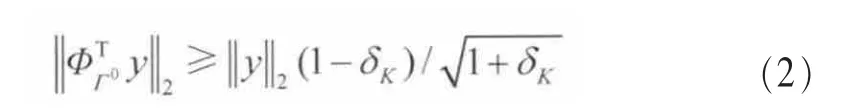
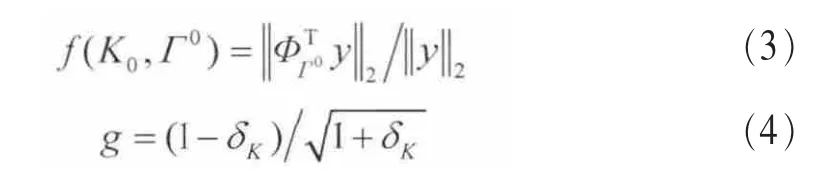



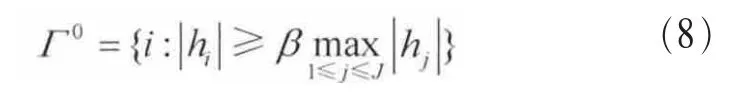
3 寬支撐集的分布式壓縮頻譜感知
4 算法仿真與性能分析
4.1 稀疏度估計性能

4.2 頻譜感知算法性能
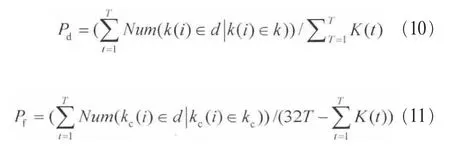
5 結束語

