大尺寸箭彈質量特性測量過程中位姿標定方法研究

王超，張曉琳，唐文彥，王軍，馬強

(哈爾濱工業大學 電氣工程及自動化學院，黑龍江哈爾濱150001)

0 引言

質量特性參數是飛行體的一組重要參數，它包括質量、質心、轉動慣量和慣性積。飛行器在使用之前都需要進行質量特性參數的測量，在工作時則根據這些參數來進行調整和控制，以達到姿態穩定并能夠按照指定的軌跡飛行。

目前質量質心多采用多點支撐法測量，轉動慣量和慣性積用扭擺法來測量，由于轉動慣量和慣性積共有6 個獨立分量，所以還需要在測量過程中變換產品的位姿。因此提高質量特性測量精度主要從3 個方面考慮:1)對測量質量質心所用到的稱重傳感器進行標定［1］;2)對計算轉動慣量和慣性積所需要參數(比如扭擺法中的扭桿系數［2-3］，三線擺法中的空擺質量、擺長等)進行標定;3)提高產品測量位姿定位精度，這依賴于固定產品的機械工裝加工和裝配精度以及機械結構。對于中小型待測產品來說，由于測量設備體積小且機械結構簡單，工裝加工及裝配精度可以達到較高的要求，因此通常情況下忽略產品位姿對測量精度的影響，只考慮前兩個因素的影響。但是對于大型質量特性一體化測量設備來說，通常采用可兩自由度旋轉的連桿結構來實現位姿變換，機械加工以及裝配所產生誤差通過連桿的相對運動放大并傳遞至終端執行器，進而導致被測產品的位姿目標值與實際位姿之間的偏差較大。因此對于大尺寸箭彈質量特性測量來說，通過標定位姿以減小位姿誤差對提高測量精度有著非常重要的意義。

1 運動學建模

產品位姿的變換依托于機械工裝結構，如圖1所示，這是一個串聯型機械結構，工裝上的2 個電機可分別帶動產品進行橫向和縱向兩自由度的旋轉，以實現變換不同測量位姿的需求。

圖1 機械工裝示意圖Fig.1 Schematic diagram of mechanical system

利用D-H 參數來建立機械結構的理想運動學模型。首先建立相關坐標系，如圖2所示，建立參考坐標系Oxyz，選擇橫軸L1作為關節1，用z0表示，x0與參考坐標系x 軸方向一致，原點O0選擇橫軸中心點，根據右手法則建立關節1 的坐標系;選擇縱軸L2作為關節2，用z1表示，x1垂直于z0和z1，O1與O0重合，利用右手法則建立關節2 坐標系O1x1y1z1，末端適配器坐標系也就是產品坐標系的坐標軸與關節1 坐標系坐標軸平行，原點為適配器上某一已知點。

圖2 連桿坐標系Fig.2 Coordinate frame of link-pole

建立坐標系后，從坐標系i -1 到坐標系i 的轉換矩陣i-1Ti就可以用利用θ、d、a、α 這4 個D-H 參數并按照一定的順序表示:

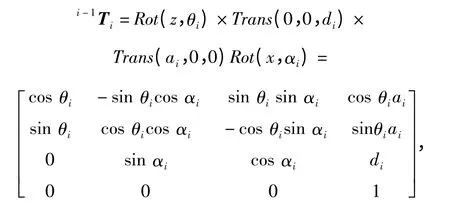
式中:θi為連桿夾角，即坐標軸xi-1與xi的夾角;ai為連桿長度，即坐標軸zi-1與zi的公垂線距離;di為連桿距離，即坐標軸xi-1與xi的公垂線距離;αi為連桿扭角，即坐標軸zi-1與zi的夾角。

從參考坐標系到產品坐標系的轉換矩陣即產品位姿可記作:

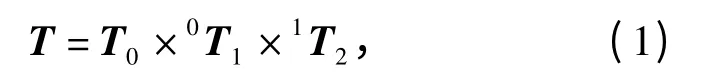
式中:T0是參考坐標系到坐標系O0x0y0z0的轉換矩陣，是一個常數矩陣;0T1、1T2是含有D-H 參數的矩陣，只要已知θ=(θ1，θ2)和par=(di，ai，αi)就可以確定產品位姿T:

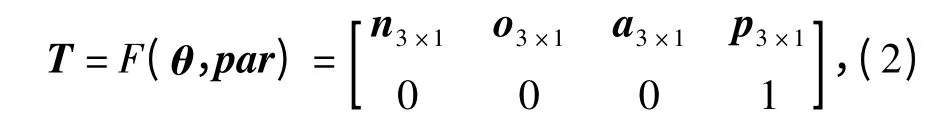
式中:n、o、a 分別是產品坐標系x、y、z 軸的方向向量;p 是坐標系原點坐標組成的列向量。

2 測量位姿對質量特性測量的影響

在測量質心時，產品需變換2 種位姿，然后分別將每個位姿下測得的數據轉換到產品坐標系下，得到最終的結果:

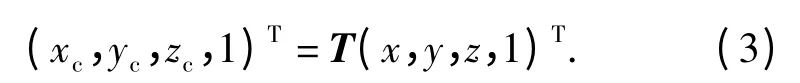
而在測量轉動慣量和慣性積時，需要變換6 個位姿，聯立6 個方程，得方程組:

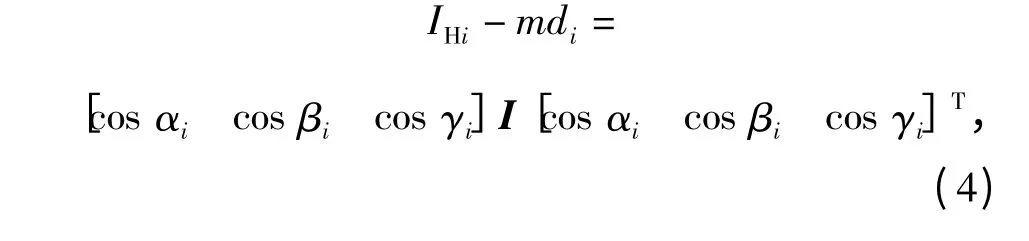
式中:αi、βi、γi分別是第i(i=1 ～6)個位姿下產品坐標系x、y、z 軸與扭擺軸的夾角;di是第i 個位姿下產品質心到扭擺軸的距離;I 為待測轉動慣量和慣性積組成的慣性張量矩陣，

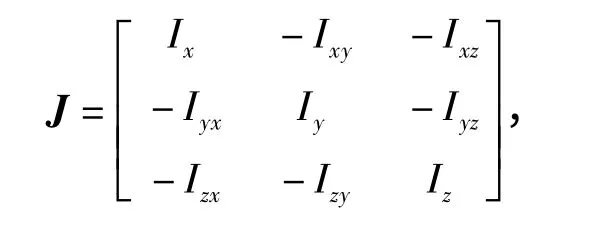
式中:Ixy=Iyx，Ixz=Izx，Iyz=Izy.

產品位姿產生偏差ΔT 會對測量結果產生如下影響:

2)質心位置的偏差會導致方程組(4)式中常數項矩陣中di存在偏差Δdi.

3)產品位姿偏差ΔT 中的姿態偏差或者叫旋轉偏差［Δn，Δo，Δa］，會產生Δαi、Δβi、Δγi變化。那么(4)式就變為

因此機械工裝D-H 參數的準確與否直接影響產品測量位姿，進而影響測量結果的準確程度。

3 運動學標定法

由于工裝D-H 參數以及運動角度都會有誤差產生，因此產品的實際位姿為

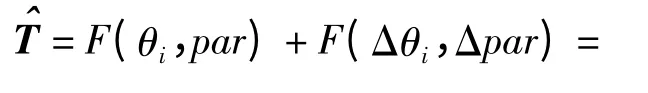
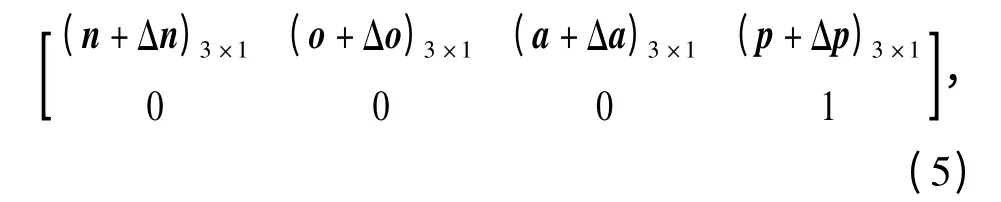
式中:Δn、Δo、Δa 為產品坐標系的姿態偏差(旋轉偏差);Δp 為產品坐標系的位置偏差(平移偏差).

當實際幾何參數與理論幾何參數偏差較小時，位姿誤差可簡化成相應的線性模型［6］

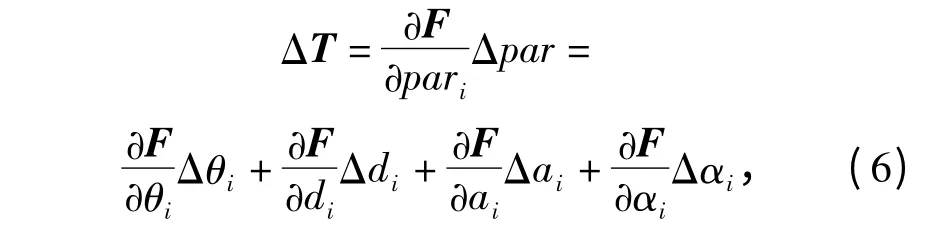
式中:Δdi、Δai、Δαi，是由于第i 個連桿的加工和安裝精度導致的，一旦安裝好后這些參數就為定值;而Δθi主要是由于工裝重力因素和減速器齒輪之間的間隙造成的，屬于非幾何參數誤差，且誤差大小是隨著旋轉角度的變化而變化的。

將減速器中齒輪的間隙及偏心導致的角度誤差記作Δθgi［7］，Δθgi= P1gsin(αi+ φ1)+ P2gsin(niαi+φ2)，式中:αi為關節旋轉的角度;ni是減速器減速比;P1g、P2g、φ1、φ2為需要標定的參數。

機械工裝自身重力和外加負載也會對該關節轉角產生偏差，記作ΔθLi，將該柔性關節簡化為線性扭簧模型，即ΔθLi=Cif(G，θi)，式中:f(G，θi)為施加在柔性關節軸上的等效力矩;G 為連桿重力;Ci為需要標定的柔度系數。因此關節旋轉角度的誤差為

根據運動學的正解的原理［8］，可以由(6)式得到產品坐標系上在任意位姿下的位置偏差與結構參數誤差值的關系:

上式可以寫成

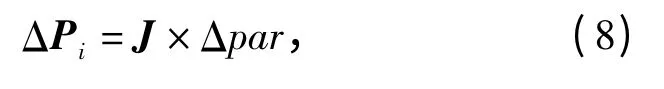
式中:矩陣J 為雅克比矩陣的一種變形形式，可視為參數誤差的傳遞矩陣;ΔPi代表產品坐標系位置偏差，即標定點坐標的實際值Pr與名義值Pn的差。

標定過程如圖3所示，將關節轉角和待標定參數的名義值θn、parn代入到系統的運動學模型中，得到標定點位置的名義值Pn，同時根據關節轉角將設備運動到指定位置，再利用激光跟蹤儀測量標定點位置的實際值Pr，將位置偏差代入到(8)式，通過解非線性方程組，得到參數的誤差值Δpar，將其代入(5)式得到產品的實際位姿。

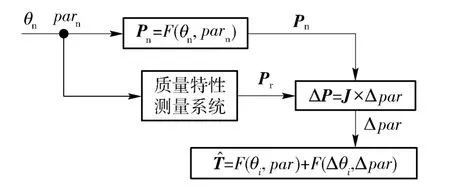
圖3 運動學標定過程Fig.3 Kinematics calibration process

4 神經網絡在位姿標定中的應用

運動學標定法雖然在原理上比較簡單，但是需要考慮的影響因素較多，尤其是在關節旋轉角誤差的分析方面，其誤差模型主要是通過經驗公式和半經驗公式得到的。這些方法都是要假設輸入與輸出之間存在一定的函數關系，這在理論上存在一定的缺陷，而且對于新出現的數據，經驗公式不能較快地吸收來改進其本身的精度。因此采用神經網絡方法來解決上述問題。

通過前文對運動學模型的分析，可以將參數誤差分為兩類:剛性參數誤差和柔性參數誤差。剛性參數誤差就是D-H 參數中d、a、α 的誤差，機械工裝加工安裝好以后，這些參數的誤差就不發生變化了;而關節旋轉角度θ 是一個變量，其誤差是與當前角度有關的一個非線性變量，所以稱之為柔性參數誤差。下面對兩種誤差分別進行標定。

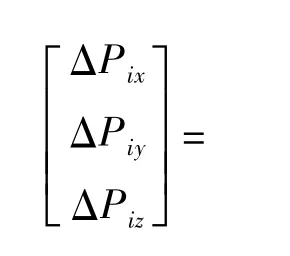
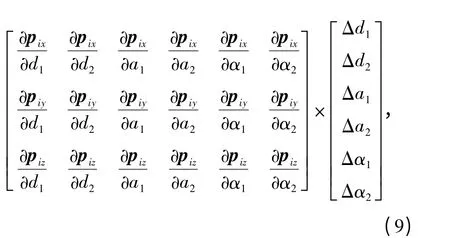
剛性誤差仍利用運動學標定，標定原理及過程同上一節，在此不再贅述。最后得到產品坐標系位置偏差模型取N 個(N≥3)標定點坐標，代入(9)式，利用最小二乘原理解該線性方程組，就可得到剛性參數誤差。

柔性參數誤差則利用BP 神經網絡進行標定，該網絡共分3 層，第1 層為輸入層，由兩個神經元組成，分別為兩個關節的旋轉角θ1、θ2. 第2 層為隱層。第3 層為輸出層，包含兩個神經元Δθ1、Δθ2，代表關節的非幾何參數誤差。隱含層的傳遞采用S 形的正切函數，輸出層傳遞函數采用線性函數，并利用梯度下降動量法訓練該網絡。

網絡學習過程如圖4所示，測量設備各關節按照名義角度θn旋轉，利用激光跟蹤儀測量運動后終端產品坐標系的實際位置Pr，將θn作為神經網絡的輸入數據，網絡的輸出數據Δθ 必須滿足產品坐標系位置偏差不大于0.01 mm.

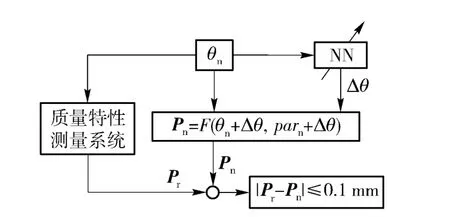
圖4 網絡學習過程Fig.4 The learning process of neural network

經過訓練后的神經網絡可以將各關節的旋轉角度θ 和誤差Δθ 的非線性關系建立起來。因此通過這種將神經網絡與運動學相結合的方法標定后，可得到任意位姿下的設備結構參數誤差Δθi和Δpar.將其值代入(5)式，就能得到產品坐標系的實際位姿。

5 標定實驗過程及誤差補償結果

為了驗證本文所述標定方法的有效性，進行了標定實驗，如圖5所示，利用控制臺改變設備姿態，并利用激光跟蹤儀進行關鍵點坐標的采集。根據標定原理，首先要選擇若干組(θ1，θ2)，實際關節的旋轉角度范圍為θ1∈［90°，180°］，θ2∈［0°，360°］. 從初始位置開始關節1 按10°的間隔角進行運動，在關節1 的每個位姿下關節2 按45°的間隔角運動，最后在運動空間內共選取72 個標定位姿。

圖5 利用激光跟蹤儀進行標定試驗Fig.5 Calibration experiment using laser tracker

利用運動學標定法來標定所有的參數，理論上16 個參數共需要6 個標定位姿就能得出結果，為了提高標定精度，從中選擇20 個位姿進行標定;神經網絡-運動學混合標定法中，同樣利用其中的20 個位姿進行剛性參數的標定，然后選取整個空間72 個位姿進行神經網絡的訓練，進行柔性參數的標定。

為驗證最終的標定效果，定義產品坐標系位置誤差EL和姿態誤差Ep為最后利用后20 個位姿來對比2 種方法的標定效果，如圖6所示。

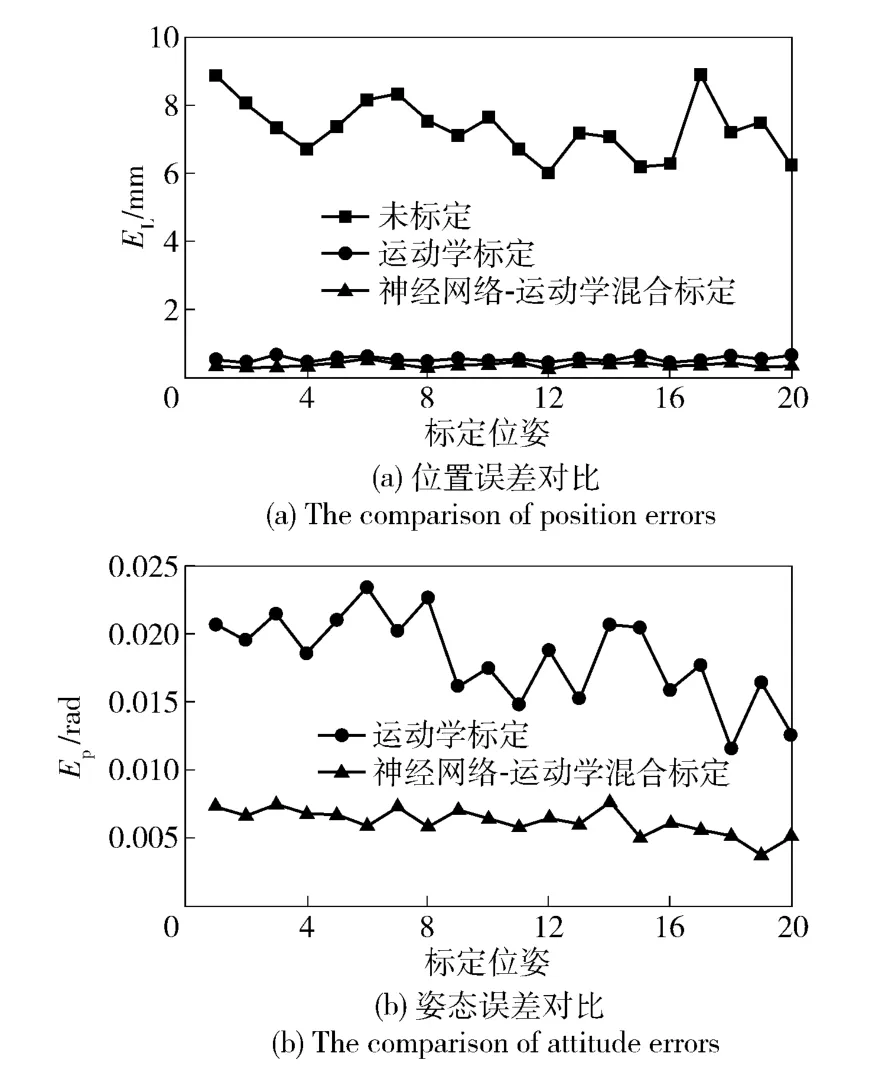
圖6 標定結果對比Fig.6 The comparison of calibration results

表1 標準件質量特性測量結果對比Tab.1 Comparison of measurement results of mass properties of standard parts

從標定結果中可以明顯看出，標定后的設備較未標定的設備位置誤差明顯減小，利用運動學標定后的設備位置誤差平均值為0.565 8 mm，姿態誤差的平均值為0.018 3 rad;而利用神經網絡與運動學相結合的方法標定后的設備，其位置誤差平均值為0.397 5 mm，姿態誤差的平均值為0.006 2 rad. 可以看出后者的標定精度高于前者。

分別在采用兩種標定方法進行位姿補償的情況下測量并計算標準件的質量特性，得到結果如表1.通過實驗對比，運動學標定法將質心測量誤差減小為標定前的10%，轉動慣量和慣性積測量誤差減小為標定前的90%和20%;利用神經網絡與運動學相結合的標定方法能將質心的測量誤差減小為標定前的7%，轉動慣量和慣性積測量誤差減小為標定前的45%和15%.

6 結論

在大尺寸箭彈質量特性參數測量領域中，提高質量特性參數測量精度一直是研究的重點，而目前的方法對于大尺寸一體化質量特性測量系統具有局限性。因此本文從測量位姿對測量精度的影響出發，分別利用運動學標定方法和神經網絡與運動學相結合標定法，通過對測量位姿的標定，提高了質量特性的測量精度。前者原理簡單，具有普遍適用性——不同的待測產品只要測量設備不變就不需要重新標定;后者由于柔性誤差受到待測產品本身的特性影響，因此針對不同的待測產品需要重新標定，但是其標定精度更高，更適合高精度測量。

References)

［1］潘文松，王昌明，包建東，等. 彈體質量、質心及質偏心測試誤差補償［J］. 機械工程師，2010(7):1 -2.PAN Wen-song，WANG Chang-ming，BAO Jian-dong，et al.Measurement error compensating for missile mass centroid and centroidal deviation［J］. Mechanical Engineer，2010(7):1 -2(in Chinese)

［2］吳斌，楊全潔. 用扭擺法測量導彈慣性積的誤差分析［J］. 彈箭與制導學報，2005，25(4):153 -155.WU Bin，YANG Quan-jie. Error analysis for testing missile’s product of inertia using torsion pendulum［J］. Journal of Projectiles，Rockets，Missiles and Guidance，2005，25(4):153 -155.(in Chinese)

［3］張心明，王凌云，劉建河，等. 復擺法測量箭彈轉動慣量和質偏及誤差分析［J］. 兵工學報，2008，29(4):450 -453.ZHANG Xin-ming，WANG Ling-yun，LIU Jian-he，et al. The measurement of inertia moment and centroidal deviation of rocket projectile with compound pendulum method and its error analysis［J］. Acta Armamentarii，2008，29(4):450 -453. (in Chinese)

［4］王超，唐文彥，張曉琳，等. 大尺寸非回轉體質量特性一體化測量系統的設計［J］.儀器儀表學報，2012，33(7):1634 -1639.WANG Chao，TANG Wen-yan，ZHANG Xiao-lin，et al. Design of mass property integration measurement system for large size nonrotatinig bodies ［J］. Chniese Journal of Scientific Instrument，2012，33(7):1634 -1639.(in Chinese)

［5］李慧鵬，唐文彥，張春富，等.導彈轉動慣量測試系統及誤差分析［J］. 兵工學報，2007，28(2):206 -208.LI Hui-peng，TANG Wen-yan，ZHANG Chun-fu，et al. A measuring system of inertia moment of missile and its error analysis［J］.Acta Armamentarii，2007，28(2):206 -208. (in Chinese)

［6］Wu C H. The kinematic error model for the design of robot manipulators［C］∥American Control Conference. San Francisco:IEEE，1983:497 -502.

［7］Judd R P，Knasinski A B. A technique to calibrate industrial robots with experimental verification［J］. IEEE Transactions on Rototics and Automation，1990，6(1):20 -30.

［8］任永杰，邾繼貴，楊學友，等. 利用激光跟蹤儀對機器人進行標定的方法［J］. 機械工程學報，2007，43(9):195 -200.REN Yong-jie，ZHU Ji-gui，YANG Xue-you，et al. Method of robot calibration based on laser tracker［J］. Chinese Journal of Mechanical Engineering，2007，43(9):195 -200. (in Chinese)

［9］Aoyagi S，Kohama A，Nakata Y，et al. Improvement of robot accuracy by calibrating kinematic model using a laser tracking system-compensation of non-geometric errors using heural hetworks and selection of optimal measuring points using genetic algorithm［C］∥Intelligent Robots and Systems (IROS)，2010 IEEE/RSJ International Conference on IEEE. Taipei，Taiwan:IEEE，2010:5660 -5665.