變纜長(zhǎng)拖纜AUV縱向運(yùn)動(dòng)建模與仿真

楊智棟, 潘 光, 杜曉旭

?

變纜長(zhǎng)拖纜AUV縱向運(yùn)動(dòng)建模與仿真

楊智棟, 潘 光, 杜曉旭

(西北工業(yè)大學(xué) 航海學(xué)院, 陜西 西安, 710072)

針對(duì)拖纜自主水下航行器(AUV)運(yùn)動(dòng)過程中引起的拖纜長(zhǎng)度變化問題, 采用集中質(zhì)量法建立了拖纜的運(yùn)動(dòng)方程, 根據(jù)剛體動(dòng)量定理及動(dòng)量矩定理建立了拖纜AUV的縱向運(yùn)動(dòng)方程, 在此基礎(chǔ)上補(bǔ)充推導(dǎo)了AUV拖纜運(yùn)動(dòng)過程的變纜長(zhǎng)邊界方程。聯(lián)立拖纜運(yùn)動(dòng)方程、AUV縱向運(yùn)動(dòng)方程及邊界方程得到變纜長(zhǎng)拖纜AUV縱向運(yùn)動(dòng)方程。基于此方程, 應(yīng)用4階Runge-Kutta法對(duì)采用相同控制律方程的無纜及有纜AUV進(jìn)行了對(duì)比運(yùn)動(dòng)仿真。仿真結(jié)果表明, 隨著運(yùn)動(dòng)過程中拖纜長(zhǎng)度的不斷增長(zhǎng), 拖纜對(duì)AUV的作用力不斷增大, 對(duì)AUV各運(yùn)動(dòng)參數(shù)的影響也不斷增大, 且對(duì)AUV軸向運(yùn)動(dòng)速度的影響最為明顯。

自主水下航行器; 拖纜; 集中質(zhì)量法

0 引言

隨著海洋工程領(lǐng)域的不斷發(fā)展, 自主水下航行器(autonomous underwater vehicle, AUV)所起到的作用越來越被各國重視。攜帶通信拖纜與母船保持通信連接的AUV, 一方面可方便母船監(jiān)控AUV在海水中的運(yùn)行狀態(tài), 與AUV實(shí)時(shí)傳輸數(shù)據(jù); 另一方面可用于AUV的回收牽引等。研究拖纜對(duì)AUV運(yùn)動(dòng)過程的影響對(duì)帶纜AUV的設(shè)計(jì)和發(fā)展有一定工程實(shí)用性。

目前國內(nèi)外針對(duì)拖纜的集中質(zhì)量模型[1-2]和有限差分模型[3-4]對(duì)拖纜長(zhǎng)度保持不變時(shí)的拖纜系統(tǒng)研究已取得了不同程度的進(jìn)展。關(guān)于收放拖纜系統(tǒng)的研究, 國內(nèi)王飛、徐剛等采用集中質(zhì)量模型對(duì)收放纜速度為已知函數(shù)的拖纜收放問題進(jìn)行了一定研究[5-6], 國外Feng Z采用有限差分法對(duì)張力決定收放速率的收放纜進(jìn)行了一定研究, 但計(jì)算結(jié)果有些擾動(dòng)[7]。

本文針對(duì)拖纜AUV運(yùn)動(dòng)過程中引起的拖纜長(zhǎng)度變化的問題, 采用集中質(zhì)量法建立拖纜運(yùn)動(dòng)模型, 結(jié)合AUV縱向運(yùn)動(dòng)方程及推導(dǎo)出的變纜長(zhǎng)邊界條件方程, 采用4階Runge-Kutta法對(duì)無纜和有纜情況的AUV進(jìn)行對(duì)比運(yùn)動(dòng)仿真研究。

1 系留系統(tǒng)運(yùn)動(dòng)方程

1.1 坐標(biāo)系建立

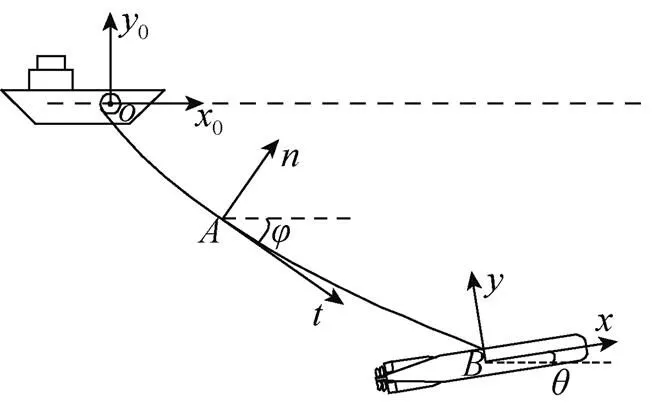
圖1 坐標(biāo)系定義

1.2 拖纜運(yùn)動(dòng)方程

1.2.1 控制方程

假定拖纜是細(xì)長(zhǎng)圓柱體, 不考慮彎矩和扭矩的影響, 可以認(rèn)為拖纜只受重力、浮力、阻力和慣性力作用。根據(jù)牛頓第二定律, 可建立在流體中運(yùn)動(dòng)的拖纜微段動(dòng)力學(xué)控制方程

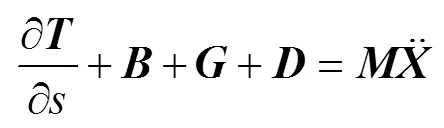
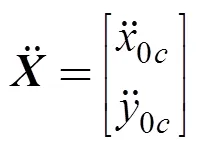
1.2.2 拖纜附加質(zhì)量

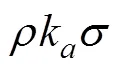
1.2.3 集中質(zhì)量法數(shù)學(xué)方程

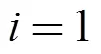
各節(jié)點(diǎn)可均布亦可不均布, 選取相鄰節(jié)點(diǎn)間應(yīng)力應(yīng)變關(guān)系作為拖纜連續(xù)性條件, 即

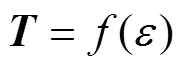
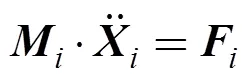
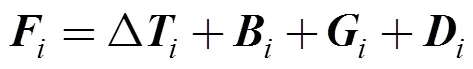
1) 拖纜張力

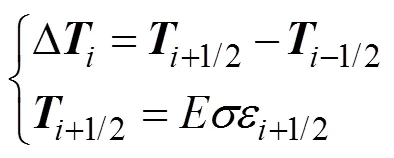
2) 浮力與重力

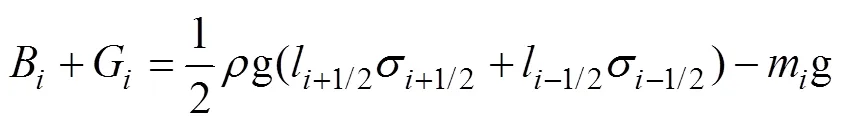
3) 流體阻力

參照文獻(xiàn)[3]中拖纜微段切向和法向流體阻力公式,在拖纜局部坐標(biāo)系下將拖纜阻力分為切向和法向兩部分

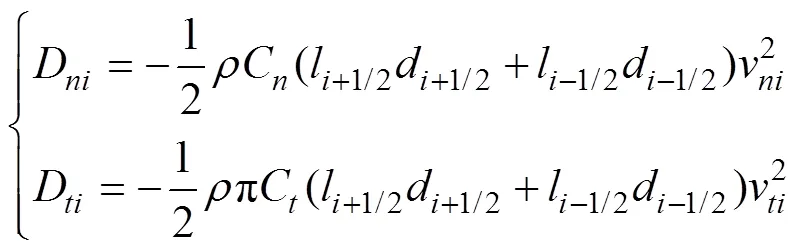
1.3 AUV縱向運(yùn)動(dòng)方程

,

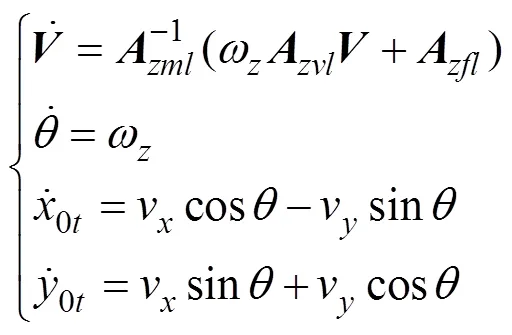
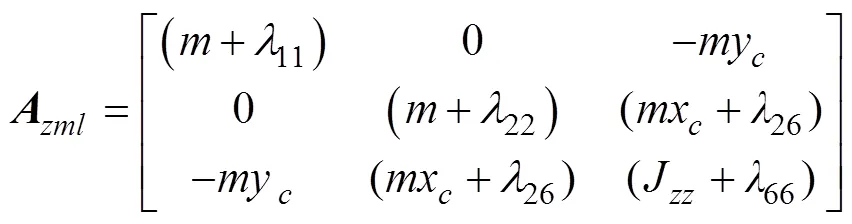
1.4 拖纜AUV運(yùn)動(dòng)方程

聯(lián)立拖纜運(yùn)動(dòng)方程(3)及AUV縱向運(yùn)動(dòng)方程(8), 即可得拖纜AUV耦合運(yùn)動(dòng)方程

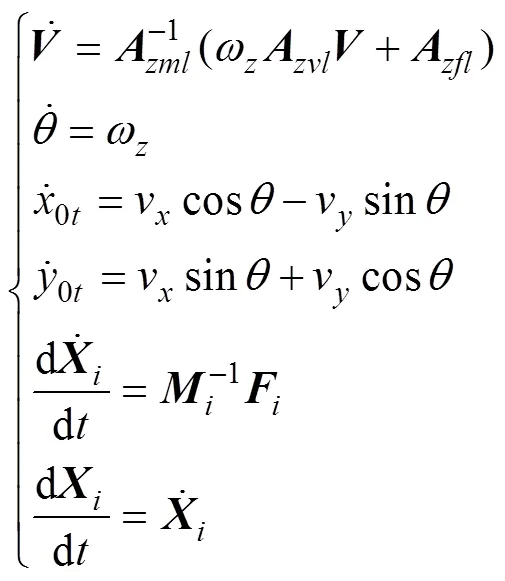
由式(9)可以看出, 拖纜AUV耦合運(yùn)動(dòng)方程為常微分方程組, 且方程個(gè)數(shù)為(4+2), 未知數(shù)個(gè)數(shù)為(4+10), 由此可知, 需添加8個(gè)輔助方程才能封閉求解。

2 放纜邊界條件及數(shù)值方法

2.1 邊界條件

2.1.1 首端邊界條件

拖纜首端與AUV相連, 所以位置、速度應(yīng)與AUV聯(lián)接點(diǎn)位置、速度保持一致, 即

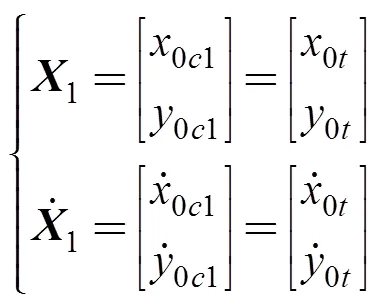
2.1.2 末端邊界條件

拖纜末端與絞盤相連, 此處假定與AUV相連的拖纜直徑相對(duì)于絞盤直徑足夠小, 可以忽略AUV拖動(dòng)絞盤放纜過程對(duì)絞盤所纏拖纜線圈直徑大小及其轉(zhuǎn)動(dòng)慣量引起的改變。以絞盤為研究對(duì)象, 根據(jù)動(dòng)量矩定理建立如下方程

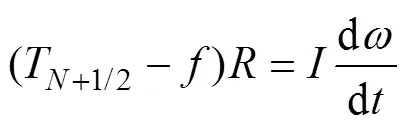
由式(11)可知, 與絞盤相接觸的拖纜第+1節(jié)點(diǎn)速度可表示為

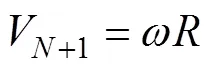
將式(12)代入式(11)中, 可得

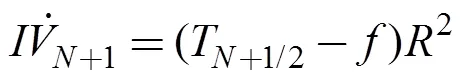
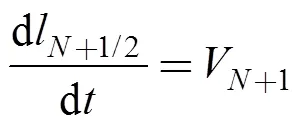
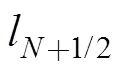
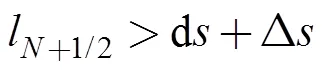
增加1個(gè)節(jié)點(diǎn), 新節(jié)點(diǎn)的位置和速度可按下式賦值

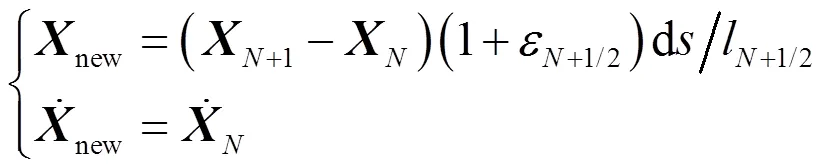
獲取新節(jié)點(diǎn)位置與速度后, 節(jié)點(diǎn)總數(shù)目加1,將新節(jié)點(diǎn)標(biāo)記為+1, 末端與絞盤聯(lián)接點(diǎn)標(biāo)記為+2。至此, 聯(lián)立拖纜AUV方程(9)、邊界方程(10)、方程(13)、方程(14)和方程(16)即可封閉求解。

2.2 數(shù)值方法

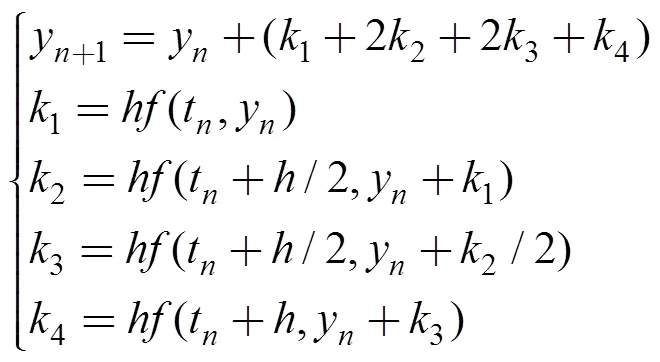
3 仿真算例

為了研究拖纜對(duì)AUV運(yùn)動(dòng)的影響, 本文對(duì)選用相同控制律方程的AUV針對(duì)無纜和有纜2種工況分別進(jìn)行運(yùn)動(dòng)仿真, 通過對(duì)比二者仿真結(jié)果來分析拖纜對(duì)AUV運(yùn)動(dòng)參量的影響。設(shè)定地面系中AUV的初始坐標(biāo)為(0,-10), 拖船絞盤中心位置為(0,0), 拖纜與AUV浮心上殼體表面的投影點(diǎn)相連。

表1 AUV運(yùn)動(dòng)參數(shù)初值

表2 拖纜參數(shù)

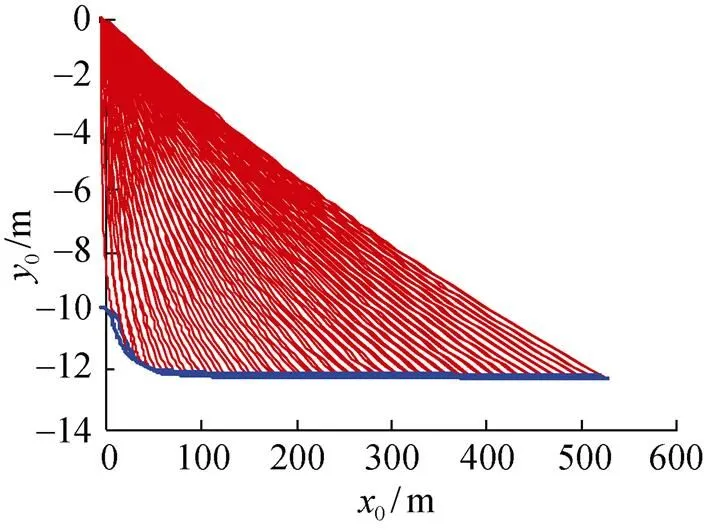
圖2 不同時(shí)刻拖纜形態(tài)圖

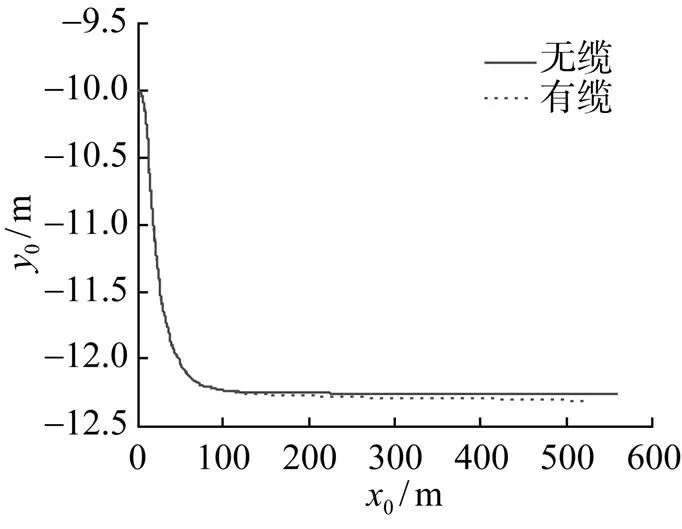
圖3 AUV縱向運(yùn)動(dòng)曲線

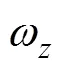
圖4 軸向速度隨時(shí)間變化曲線

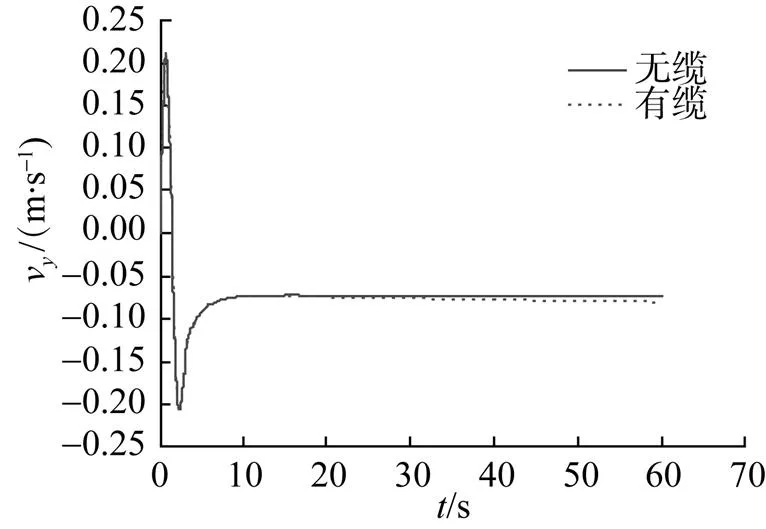
圖5 法向速度隨時(shí)間變化曲線

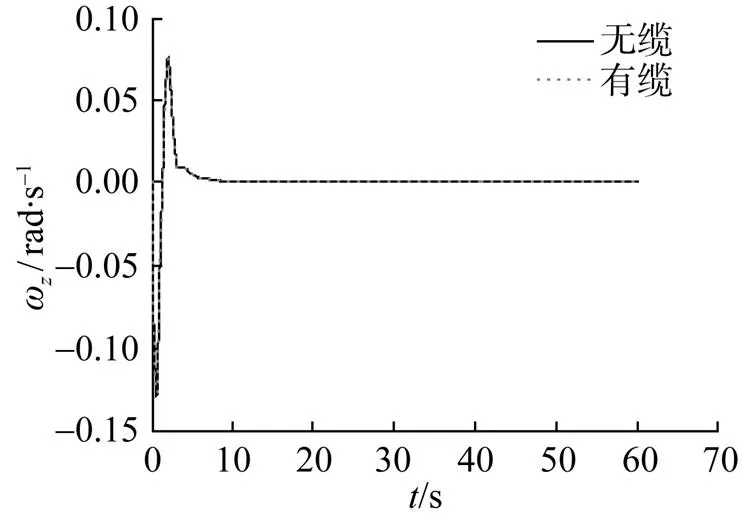
圖6 俯仰角速度隨時(shí)間變化曲線

Fig. 6 Curves of pitch angular velocity versus time

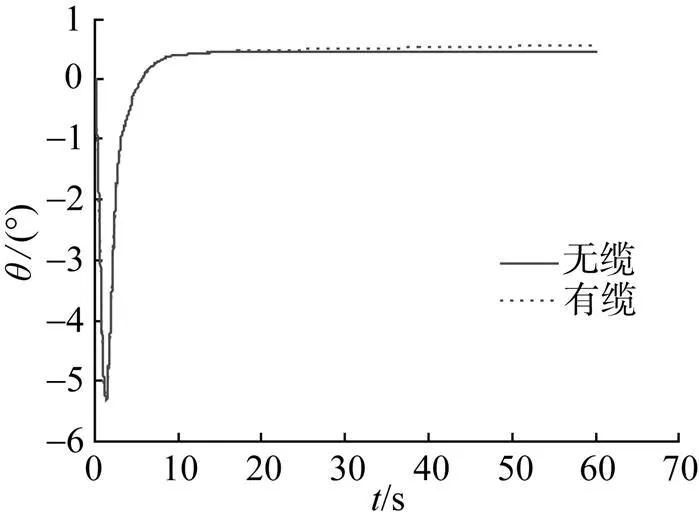
圖7 俯仰角隨時(shí)間變化曲線

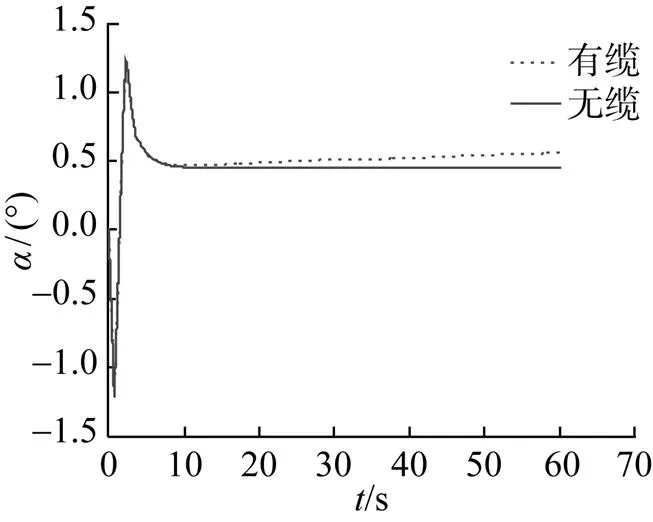
圖8 攻角隨時(shí)間變化曲線

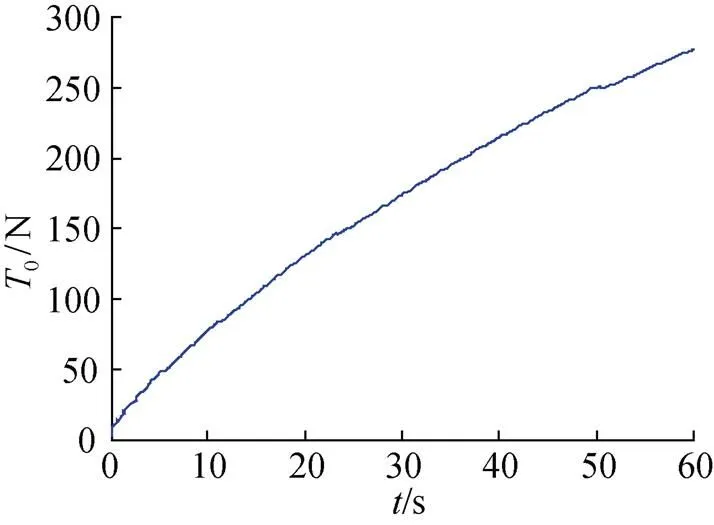
圖9 拖點(diǎn)拉力隨時(shí)間變化曲線

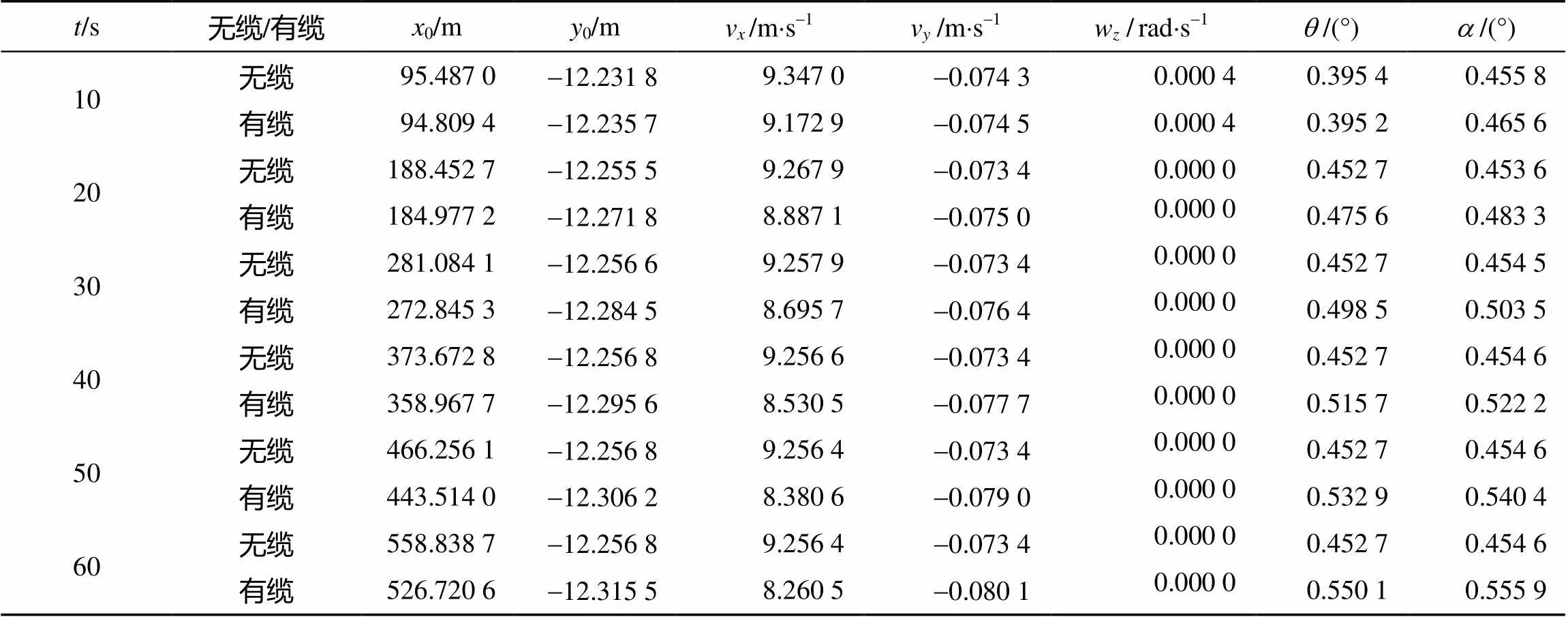
表3 對(duì)應(yīng)離散時(shí)刻AUV運(yùn)動(dòng)參數(shù)值

4 結(jié)論

本文采用集中質(zhì)量法建立了拖纜的運(yùn)動(dòng)方程, 根據(jù)剛體動(dòng)量定理及動(dòng)量矩定理建立了拖纜AUV的縱向運(yùn)動(dòng)方程, 在此基礎(chǔ)上補(bǔ)充推導(dǎo)了AUV拖纜運(yùn)動(dòng)的邊界方程, 聯(lián)立拖纜運(yùn)動(dòng)方程、AUV運(yùn)動(dòng)方程及邊界方程得到變纜長(zhǎng)拖纜AUV縱向運(yùn)動(dòng)方程。基于此方程采用4階Runge- Kutta對(duì)選用相同控制律方程的無纜及有拖纜AUV進(jìn)行了對(duì)比運(yùn)動(dòng)仿真, 得到仿真結(jié)論如下:

1) 拖纜AUV相較無纜AUV運(yùn)動(dòng)情況, 拖纜對(duì)AUV各運(yùn)動(dòng)參數(shù)均有不同程度的影響, 且隨著拖纜長(zhǎng)度的不斷增長(zhǎng), 拖纜對(duì)AUV各運(yùn)動(dòng)參量的影響會(huì)不斷增大。

2) 拖纜對(duì)AUV各運(yùn)動(dòng)參量的影響中, 對(duì)AUV軸向速度的影響最明顯, 隨著拖纜長(zhǎng)度的增長(zhǎng), AUV軸向速度不斷減小, 為了避免拖纜較長(zhǎng)對(duì)AUV運(yùn)動(dòng)穩(wěn)定性的影響, 應(yīng)限定AUV相對(duì)于母船的運(yùn)動(dòng)范圍或選擇直徑和線密度小的拖纜來增加AUV運(yùn)動(dòng)范圍。

3) 隨著拖纜長(zhǎng)度的增長(zhǎng), 拖纜AUV與纜繩相連點(diǎn)拖纜張力不斷增大。

4) 本文所建立的變纜長(zhǎng)拖纜AUV縱向運(yùn)動(dòng)方程可以用于仿真和分析拖纜AUV的運(yùn)動(dòng)過程,同理也可用于仿真和分析ROV的運(yùn)動(dòng)過程。

[1] Walton T S, Polachech H. Calculation of Transient Motion of Submerged Cables[J] . Mathematics of Computation, 1960(14): 27-46.

[2] Sun Y, Leonard J W, Chiou R B. Simulation of Unsteady Oceanic Cable Deployment by Direct Integration with Suppression[J]. Ocean Engineering, 1994, 21(3): 243-256.

[3] Ablow C M, Schechter S. Numerical Simulation of Undersea Cable Dynamics[J]. Ocean Engineering, 1983, 10 (6): 443-457.

[4] Wu J M, Chwang A T. A Hydrodynamic Model of a Two-Part Underwater Towed System[J]. Ocean Engineering, 2000,27(5): 455-472.

[5] 王飛. 海洋勘探拖曳系統(tǒng)運(yùn)動(dòng)仿真與控制技術(shù)研究[D]. 上海: 上海交通大學(xué), 2006.

[6] 徐剛, 葛彤, 朱繼懋, 等. “海龍-3500”深海潛水器的變長(zhǎng)纜運(yùn)動(dòng)建模與仿真[J]. 造船技術(shù), 2005(5): 21-26. Xu Gang, Ge Tong, Zhu Ji-mao, et al. Motion Modeling and Simulation of "Sea-Dragon 3500" ROV with Variable Length Cable[J]. Marine Technology, 2005(5): 21-26.

[7] Feng Z, Allen R. Evaluation of the Effects of the Communication Cable on the Dynamics of an Underwater Flight Vehicle[J]. Ocean Engineering, 2004, 31(8-9): 1019-1035.

[8] 潘光, 楊智棟, 杜曉旭. UUV水下帶纜回收縱向運(yùn)動(dòng)研究[J]. 西北工業(yè)大學(xué)學(xué)報(bào), 2011, 29(2): 245-250.Pan Guang, Yang Zhi-dong, Du Xiao-xu. Longitudinal Motion Research on UUV Underwater Recovery with a Deployable Tether[J]. Journal of Northwestern Polytechnical University, 2011, 29(2): 245-250.

[9] 杜曉旭, 宋保維, 胡海豹, 等. AUV拖曳GPS浮標(biāo)系統(tǒng)仿真研究[J]. 西北工業(yè)大學(xué)學(xué)報(bào), 2008, 26(1): 88-92.Du Xiao-xu, Song Bao-wei, Hu Hai-bao, et al. Simulation of an AUV Dragging a GPS Buoyage System[J]. Journal of Northwestern Polytechnical University, 2008, 26(1): 88-92.

[10] 杜曉旭, 宋保維, 潘光. 拖曳式導(dǎo)航浮標(biāo)對(duì)回轉(zhuǎn)體UUV操縱性的影響[J]. 兵工學(xué)報(bào), 2010, 31(9): 1164-1168.Du Xiao-xu, Song Bao-wei, Pan Guang. Effects of Dragging Navigation Buoyage on Maneuverability of Body of revolution UUV[J]. Acta Armamentarii, 2010, 31(9): 1164 -1168.

[11] 歐陽潔, 聶玉峰, 車剛明, 等. 數(shù)值分析[M]. 北京: 高等教育出版社, 2009.

(責(zé)任編輯: 陳 曦)

Longitudinal Motion Modeling and Simulation of Tethered AUV with Length-Variable Towing Cable

YANG Zhi-dongPAN GuangDU Xiao-xu

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

A numerical model oftowing cable is establishedbased on thelumped mass method to simulate the variation of cable length for tethered autonomous underwater vehicle(AUV). And a longitudinal motion model of the AUV is established according to the rigid body momentum theorem and the moment of momentum theorem. In addition, the boundary equation of the towing cable for the AUV is deduced based on the two models. The longitudinal motion equations are obtained by jointing the towed motion equation, the longitudinal motion model and the boundary equation of the towing cable. The motions of a tethered AUV and an untethered AUV are simulated and compared by using same control law equation and the fourth order Runge-Kutta method. The results show that the effects of towing cable on the motion parameters of the tethered AUV become greater as the length of towing cable increases, especially for the axial velocity of the tethered AUV, and the acting force on the tethered AUV gets greater.

autonomous underwater vehicle; towing cable; lumped mass method

TJ630

A

1673-1948(2014)01-0014-06

2013-01-14;

2013-03-16.

高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金(20126102120021).

楊智棟(1987-), 男, 在讀博士, 主要從事水下航行器發(fā)射與回收技術(shù)研究工作.