評價激勵師生合作打造和諧課堂策略
——以“平方差公式”課堂教學實錄（三）為例

訥河市同義鎮中心學校

評價激勵師生合作打造和諧課堂策略
——以“平方差公式”課堂教學實錄（三）為例

訥河市同義鎮中心學校王志明

教學目標：

1.經歷探索平方差公式的過程，進一步發展學生的符號感和推理能力、歸納能力.

2.了解公式的幾何背景，體會數形結合的思想方法，并能運用公式進行計算.

3.通過乘法公式的運用，掌握公式的結構特征，培養學生運用公式的計算能力.

4.通過多項式的乘法公式，再運用公式計算多項式乘法，培養學生從特殊到一般，從一般到特殊的思維能力.

教學重點：平方差公式.

教學難點：對于項的符號、位置、系數、指數發生變化時，結果的準確把握.

教學關鍵：抓住公式的特征，結果為相同項的平方為被減數，相反項的平方為減數.

教學方法：觀察、思考、探究、討論、歸納、主動地進行學習.下面是本節課的課堂實錄：

一、小組合作、評價導入

師：同學們好，在進行新課之前，我們先進行一個小小的比賽.以各小組為單位，進行下面的計算，請看屏幕上的投影.

（1）101×99（2）1001×999

（各小組給出計算結果.教師口述結果，請各小組檢驗結果.）

生：老師您是否記住了結果？

師：不是，而是根據兩數相乘的特征直接說出結果.我把上面的計算分別轉化為：

（1）101×99=（100+1）（100-1）

（2）1001×999=（1000+1）（1000-1）

師：請同學們觀察一下這些計算的特點.

生：是兩個數的和與這兩個數的差的積.

師：那么請同學們根據多項式乘以多項式的法則來計算（投影教材第107頁思考題），并根據乘積的特征和結果，探究一下你發現的規律.

3名同學分別說出結果，再找一名同學說規律.

師：太好了！同學們真棒！這就是我們這節課要學習的平方差公式.

師：板書平方差公式.（讓學生從觀察開始，先通過各小組合作得出結果，再與教師速算給出的結果進行對比認證，感受平方差公式的作用，引出學生掌握公式的需求.很多學生在教師板書公式時已經開始默默記憶公式了.）

二、發揮引領、學生為本

師：哪位同學能用符號語言寫一下這個公式呢？

生：（a+b）（a-b）=a2-b2，當然也可以是（x+y）（x-y）= x2-y2.

師：哪位同學能用文字語言來敘述一下呢？

生：兩數的和與這兩個數的差的積，等于這兩個數的平方差.（避免學生對公式的單純記憶，更要注重對數學問題的內在含義的理解.）

師：能否用幾何圖形的面積來驗證這個公式呢？請同學們對教材第107頁的思考進行探究（投影，一名學生到臺前給學生們解讀.）.

3) 當混合物流速或爬坡高度增加時爬坡管內二次流強度變強，泥漿混合更充分，爬坡管出口處顆粒體積分數分布的不對稱度降低。當泥漿體積分數增加時，雖然二次流強度進一步增加，但重力的影響起到了主導作用，使得高體積分數泥漿在沉管中較快恢復到直管中充分發展態。

師：同學們再看一個經常見到的圖形（投影）.

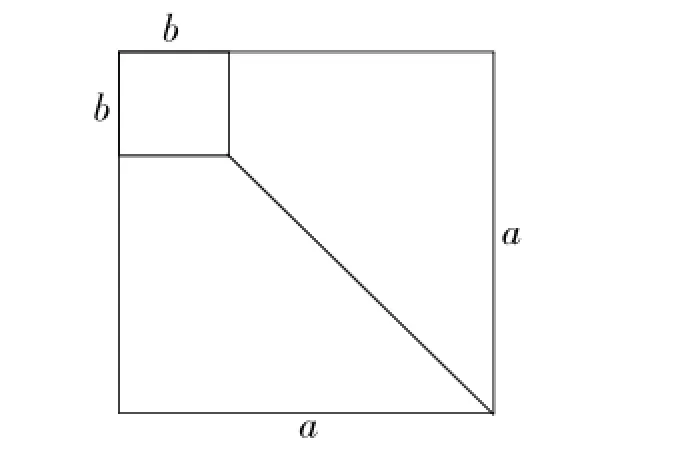
生：兩個正方形面積的差等于兩個相同的梯形面積的和，即：a2-b2=（a+b）（a-b）.

師：非常好.

三、深入解剖、突破難點

師：請同學們看下面的乘法，能否用平方差公式計算？結果是怎樣的？

（1）（a+b）（-a+b）（2）（-a+b）（-a-b）

（3）（2a+3b）（2a-3b）（4）（a2+b2）（a2-b2）

（5）（-a+b）（a-b）（6）（2a-b）（2a+c）

每個小組隨機題號完成題目.

生：兩個因式的乘積中，必須有相同的項和相反的項，并且積中相同項的平方作為被減數，相反項的平方作為減數.

生：在求積的過程中注意因式中的項的位置、符號、指數、系數的變化等.

師：回答得太好了！請同學們為這兩位同學鼓掌！兩位同學指出了我們這節課的要點、難點和解決問題的關鍵.

四、例題導航、強化訓練

師：請同學們看例題，教材第108頁例1.

三名學生到黑板前來板演.

師：再看下面的例子（投影教材第108頁例2.兩名學生到黑板前來板演.）

師：完成第108頁練習題.

（學生板演解答.）

師：用簡便的方法計算：9992=？我跟大家一起算，看誰做得快!

生：只有一個平方數，且999差1為整數1000，因此可以：9992-12+1再進行計算.

師：恭喜同學們，在本節課里，我們已經超額完成了學習任務.

五、課堂總結、布置作業

師：本節課在我們師生的觀察思考、合作探究活動中，學習了具有“兩數和與這兩個數的差的積等于這兩個數的平方差”這樣的乘法，同學們談一談你的收獲吧.

（兩名學生說心得、總結.）

師：我們今天的作業是：

（1）教材第112頁第1題.

（2）求解兩個多項式乘法問題時，在什么情況下能用平方差公式？在什么情況下不能用平方差公式？請你給出說明.