巨災債券定價參數敏感性分析——以我國洪水災害為例＊

邢天才，康晗彬

(東北財經大學金融學院，遼寧 大連 116025)

巨災債券定價參數敏感性分析
——以我國洪水災害為例＊

邢天才，康晗彬

(東北財經大學金融學院，遼寧 大連 116025)

巨災債券是巨災風險轉移資本市場上交易最活躍、使用最廣泛的金融創新產品，其定價涉及的影響因素較為復雜。本文基于資產、負債和利率理論引入巨災債券定價模型，并以我國洪水災害為例對模型參數敏感性進行了分析，分別研究了觸發水平、利率期限和資產負債比對巨災債券定價的影響規律。參數敏感性研究結果表明:巨災債券價格隨觸發水平、資產負債比的提高而增大，隨利率水平的提高而降低;我國洪水災害債券適宜的觸發水平在萬億元量級，這主要是由我國洪水災害損失分布決定的。本文研究對于我國巨災債券發行具有精算定價及政策指導等參考作用。

巨災債券定價;資產負債比;參數敏感性;蒙特卡羅模擬方法

策研究。E－mail:xingtiancai@126.com

康晗彬 (1976－)，女，遼寧鞍山人，博士研究生，主要從事巨災風險管理與保險精算研究。E－mail:hbkang2007@hotmail.com

一、引 言

我國是世界上自然災害最嚴重的國家之一，其中洪水災害導致的經濟損失位居首位，大約2/3的國土面積有著不同類型和不同危害程度的洪水災害。面對我國重大的洪水災害損失，單純依靠保險市場很難有效分散洪水災害風險，有必要借鑒發達國家的成功經驗，借助資金雄厚的資本市場發行巨災證券以分散巨災風險。巨災債券是當前國際金融市場上應對巨災風險最為典型的巨災風險證券化產品，其定價機制是國內外研究者關注的焦點。早期，Cummins和 Geman［1］、Louberge 等［2］、Briys［3］、Cox 和 Pedersen［4］在利率期限結構和巨災風險概率結構基礎之上，討論了巨災債券的均衡和無套利定價模型;Lee和Yu［5］在分別考慮違約風險、道德風險和基差風險的前提下采用蒙特卡羅模擬方法對巨災債券定價進行了研究;Vaugirard［6］利用套利方法對巨災債 券 定 價 進 行 了 研 究;Morton［7］、 Wang［8］、Christofides和 Smith［9］與 Christofides［10］分別提出了具有代表性的巨災債券定價模型;Egami和Young［11］、Jarrow［12］以及 Zhu［13］又做出了進一步研究。

在巨災債券定價機制中，觸發事件和利率期限結構是影響其價格水平的重要因素。近年來隨著水文學研究的不斷深入，能夠更準確地估計洪水災害損失、確定觸發事件水平。李永等［14］進行了多事件觸發巨災債券設計與定價研究。債券的利率期限結構模型主要分為靜態模型和動態模型兩種。在金融市場發達的國家，動態利率模型廣泛地用于固定收益證券和利率衍生品及含有嵌入期權的金融衍生品的定價分析，如巨災債券可以視為債券和嵌入期權的合成。其中較為典型的動態利率模型包括Vasicek模型［15］、CIR隨機利率模 型［16］和 CKLS 模 型［17］。Poncet 和 Vaugirard［18］使用了HJM和CIR隨機利率模型 (以下簡稱CIR模型)在巨災衍生品定價中，比較了兩種利率模型對價格的影響。

本文擬在資產負債管理基礎上，運用蒙特卡羅模擬方法對巨災債券定價進行模型研究，并以我國洪水災害為例對模型參數敏感性進行分析，重點研究資產負債比、觸發事件水平和利率水平等參數對巨災債券定價的影響規律。

二、巨災債券定價理論模型

巨災債券通常是由 (再)保險公司或SPV(特殊目的機構)發行。SPV是再保險公司為發行巨災債券而成立的特殊目的機構，一方面它受(再)保險人的委托發行債券來分散風險、籌集資金;另一方面它又肩負著在約定條件下向(再)保險人進行賠付的義務。本文所述的資產、負債、利率和累計損失動態模型涵蓋了以上機構，具有普遍性并且采用風險中性定價措施，其模型構建主要基于Lee和Yu［5］的資產負債模型并進行了改進。Lee和 Yu［5］提出的巨災債券模型假設 (再)保險公司或SPV負債在整個債券發行期內保持不變，而本文擬采用負債—利率動態模型來描述債券發行期內負債的動態變化。

(一)資產、負債動態理論模型

資產負債管理是一種協調資產與負債決策的管理活動，是一個持續完善和調整的動態過程，因此本文采用資產負債動態模型。

1.資產動態模型

在考慮資產價值問題時，除了典型的維納過程外，還要考慮隨機利率的影響，因為其在巨災債券發行人投資固定收益中占很大比重。巨災債券投資中非常注意收益高、利息率敏感的商業票據和國債等投資。考慮隨機利率影響的巨災債券發行人資產價值模型如下式所示:

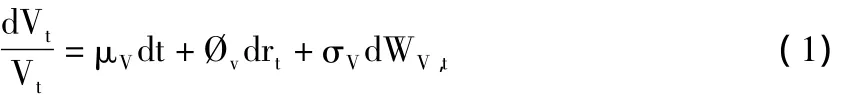
本文利率模型采用CIR模型，它是在連續時間框架下利用一般均衡方法構建的利率期限結構模型。同Vasicek模型相比，其優勢是可避免負利率的產生。CIR模型如下式所示:

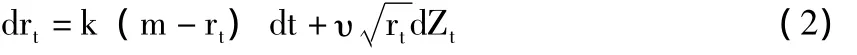
其中，k表示平均回彈系數;m表示長期利率均值;υ表示利率的波動性參數;Zt表示利率模型維納過程，它獨立于上述資產模型維納過程WV，t。結合 (1)和 (2)式 (再)保險人的資產動態模型表示為:

其中，參數λr表示利率風險市場價格，在CIR模型中是常量;Z*t表示風險中性測度Q下的維納過程。由此資產動態模型經過風險中性定價改變為:

2.負債動態模型

本文的負債定義為巨災債券發行人的巨災債券償付額與其他未來賠付額之和的現值，其動態模型如下式所示:

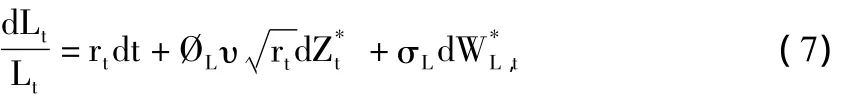
(二)巨災累計損失動態模型

(三)巨災債券定價模型

在風險中性世界中，通過各種情境下的賠付期望貼現值來計算巨災債券價格。本文以一年期無中間給付的巨災債券為例，給出不考慮風險因素和考慮違約風險因素的巨災債券定價，其模型建立主要基于Lee和Yu［5］的相關研究。

1.不考慮風險因素的巨災債券定價

不考慮風險因素的巨災債券在成熟期T時的賠付額可表示為:

其中，K表示巨災債券的觸發水平;CT表示到成熟期的累計損失;rp表示當累計損失到達觸發水平K時，債券持有人得到的本金賠付比例;L表示債券發行人總負債的面值;α表示巨災債券面值占總負債面值的比例。由此，根據風險中性定價措施Q，巨災債券價格在發行初期(t=0)可表示為:

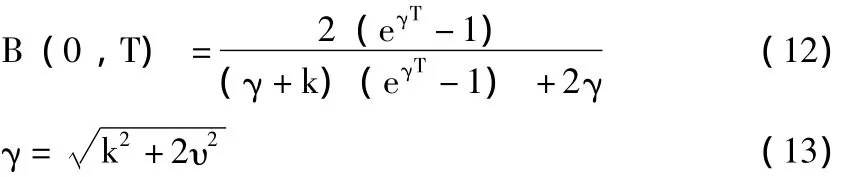
2.考慮違約風險因素的巨災債券定價

巨災債券通常是指投資在可信任的基金、以償付有限索賠和歸還本金給債券持有者為目的的債券。在巨災債券發行人破產或違約時，巨災債券持有人同其他債券持有人相比具有優先權;如果巨災債券發行人沒有破產，當潛在損失低于觸發水平時，債券持有者能得到巨災債券的所有本金;否則他們只能被償還部分本金。因此考慮違約風險時巨災債券的違約風險賠付額表示為:

其中，POi，T表示到期時根據實際損失對巨災債券的賠付額;Vi，T表示到期時債券發行人的資產價值;Ci，T表示到期時債券發行人的累計損失;L、α、K和rp定義與前述相同。

根據巨災債券的償付結構和資產、利率動態模型，巨災債券定價可表示為:

三、數值模擬結果與分析

將本文資產負債動態模型與各種情境下的巨災債券賠付額模型相結合，再考慮我國洪水災害的損失程度和頻率分布，即可在資產管理視角下對不同風險因素作用下的巨災債券進行精算定價研究和模型參數敏感性研究。本文采用《中國財產保險重大災因分析報告 (2008)》［19］中1990—2008年我國洪水災害實際損失數據進行統計。我國洪水災害損失程度服從對數正態分布，頻數符合負二項分布，即ct洪水和N(t)洪水可表示為:

我國洪水災害年損失額分布統計直方圖和累計概率圖如圖1所示，其年損失額均值為4.41×1011元。

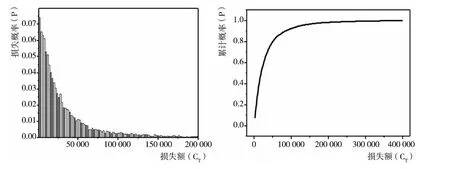
圖1 我國洪水災害年損失額分布統計直方圖和累計概率圖

本文巨災債券定價估值采用蒙特卡羅模擬方法，并利用Matlab軟件編程實現。模擬過程假設洪水巨災債券的發行期是一年，一星期為基礎單位，每一基礎單位都運行20 000次，具體模擬計算步驟參見康晗彬和邢天才的相關研究。模型相關參數初值如表1所示，運用該模型參數分別對不考慮風險因素、考慮違約風險的巨災債券定價進行了數值模擬與分析比較，基于我國洪水災害的損失程度和頻率分布研究觸發水平、利率期限和資產負債比等模型參數對巨災債券定價的敏感性。

表1 模型參數意義及賦值

(一)觸發事件水平對洪水巨災債券定價的敏感性分析

巨災債券觸發事件是決定對巨災損失是否進行賠付和賠付多少的標尺，是巨災債券區別于資本市場的其他類型債券的核心特征，也是影響巨災債券能否發行成功的決定因素。單一觸發事件的巨災債券和多觸發事件的巨災債券各有優劣。發起人一般會希望一只債券中包括的風險事件越多越好，這樣不僅能有效地降低交易成本，而且能使不同區域的巨災事件共享保障限額;投資者則正好相反，他們更傾向于單一事件觸發機制的債券，因為單一事件觸發機制能使他們更容易根據自己的投資組合偏好對特定巨災風險進行評估。

本文研究實際損失觸發事件K對我國洪水巨災債券的無風險、考慮違約風險兩種情境下定價的影響規律。由表2模擬結果可以看出，隨著觸發事件K的增大，無風險、考慮違約風險情境下巨災債券定價均不斷提高。這主要是由于隨著觸發事件K的不斷增大，洪水巨災債券對發生巨災損失賠付的概率降低，使投資者更愿意購買洪水巨災債券，從而使洪水巨災債券的價格越來越高。模擬結果表明，我國洪水巨災債券適宜的觸發事件K在萬億元量級，相應的洪水巨災債券發行人的負債規模也在該量級上。此外，從表2還可以看到，違約風險因素對洪水巨災債券的價格有顯著影響且使洪水巨災債券價格降低，尤其是在洪水巨災發生概率高的情況下。

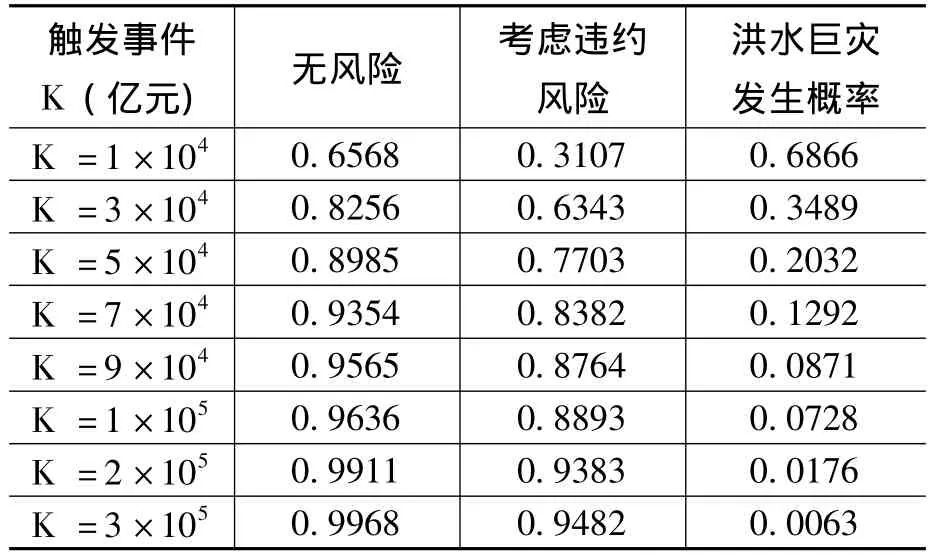
表2 觸發事件K的敏感性分析

(二)利率模型參數對洪水巨災債券定價的敏感性分析

本文假設發行的洪水巨災債券是一年期零息債券，當T=1時，由 (11)、(12)、(13)式

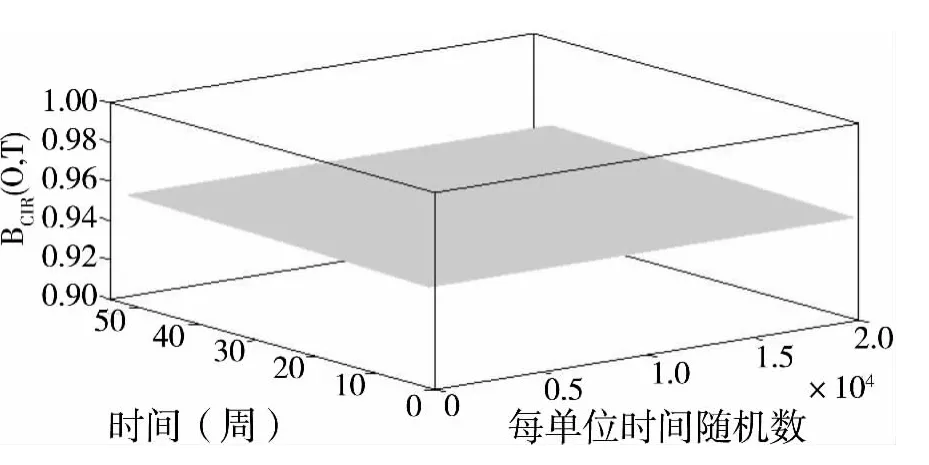
圖2 初始瞬時利率r0和長期利率均值m為5%的BCIR(0，T)分布

2013年我國發行的國債一年期利率達到7.1%，以此為依據，本文對初始瞬時利率r0和長期利率均值m分別賦值為5%、6%、7%和8%，研究利率參數對考慮違約風險情境下洪水巨災債券定價的敏感性分析。由表3可以看到，當資產負債比為1.1、觸發水平為10萬億元規模時，違約風險情境下初始瞬時利率r0與長期利率均值m為5%時洪水巨災債券定價Pi(0)=0.8893、初始瞬時利率r0與長期利率均值m為8%時Pi(0)=0.8633;當初始瞬時利率r0與和表1的賦值可以得到A(t，T)和B(t，T)為常數，所以可計算得到無風險零息債券價格BCIR(0，T)也近似為常數。根據本文前述洪水巨災債券的發行期是一年，一星期為基礎單位，每一基礎單位都運行20 000次。圖2和圖3分別給出初始瞬時利率r0和長期利率均值m為5%和8%時，BCIR(0，T)值與時間 (周)的相互關系圖。由圖2和圖3可見，當初始瞬時利率r0和長期利率均值m為5%時，無風險零息債券價格BCIR(0，T)分布區間為 (0.9513，0.9555)，其均值為0.9537;當初始瞬時利率r0和長期利率均值m為8%時，無風險零息債券價格BCIR(0，T)分布區間為 (0.9232，0.9275)，其均值為0.9252。長期利率均值m為6%、觸發水平為10萬億元規模時，違約風險情境下資產負債比為1.1時洪水巨災債券定價Pi(0)=0.8806、資產負債比為1.4時Pi(0)=0.8916。由此可見，當初始瞬時利率r0與長期利率均值m逐步增大時，考慮違約風險的洪水巨災債券價格逐步降低，這一結論也正符合零息債券的特點。由表3同時可以看出，洪水巨災債券價格隨資產負債比的提高而增大，表明有效的資產負債管理可以分散違約風險。

圖3 初始瞬時利率r0和長期利率均值m為8%的BCIR(0，T)分布

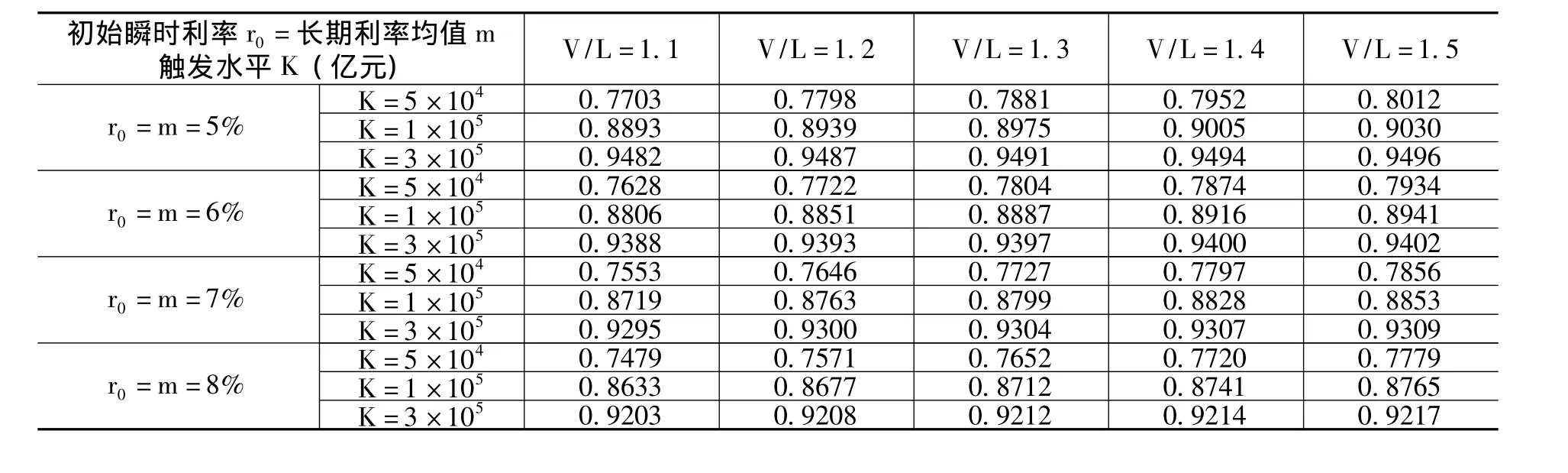
表3 違約風險情境下洪水巨災債券定價的利率敏感性分析

四、結論與建議

本文基于資產、負債和利率理論引入巨災債券定價模型，并以我國洪水災害為例對觸發水平、利率期限、資產負債比等模型參數的敏感性采用蒙特卡洛方法進行了數值分析。模擬結果表明:第一，我國洪水巨災債券適宜的觸發機制K在萬億元量級，相應的洪水巨災債券發行人的負債規模也在該量級上，這主要是由我國洪水巨災損失程度和頻數分布決定的。第二，洪水巨災債券價格隨觸發水平的提高而增大，隨利率水平的提高而降低。第三，洪水巨災債券價格隨資產負債比的提高而增大，表明有效的資產負債管理可以分散違約風險。

本文研究對于我國洪水巨災債券發行具有精算定價及政策制定參考作用。第一，本文應用CIR模型可以有效貼近現實利率、避免負利率的產生，從而提高定價結果的合理性，因此洪水巨災債券發行主體 (SPV)在進行債券定價時，需要合理選擇利率期限模型并提高模型參數的合理性，從而控制利率模型帶來的定價偏離。第二，本文在資產負債視角下對我國洪水巨災債券的單一事件觸發機制的量化研究表明，監管機構應加強對SPV資產負債狀況的監管，SPV應通過有效的資產負債管理提高其所發行洪水巨災債券在資本投資市場的吸引力和競爭力。

［1］Cummins，D.J.，Geman，H.Pricing Catastrophe Insurance Futures and Call Spread:An Arbitrage Approach［J］.The Journal of Fixed Income，1995，(4):46－57.

［2］Louberge，H.，Kellezi，E.，Gilli，M.Using Catastrophe－Linked Securities to Diversify Insurance Risk:A Financial Analysis of CAT Bonds［J］.Journal of Insurance Issues，1999，22(2):125－146.

［3］Briys，E.From Genoa to Kobe:Natural Hazards，Insurance Risks and the Pricing of Insurance－Linked Bonds ［M］. London: Lehman Brothers International，1997.

［4］Cox，S.H.，Pedersen，H.W.Catastrophe Risk Bonds［J］.North American Actuarial Journal，2001，4(4):56－82.

［5］Lee，J.P.，Yu，M.T.Pricing Default－ Risky Cat Bonds with Moral Hazard and Basis Risk［J］.Journal of Risk and Insurance，2002，69(1):25－44.

［6］Vaugirard，V.E.Pricing Catastrophe Bonds by an Arbitrage Approach［J］.The Quarterly Review of Economics and Finance，2003，43(1):119－132.

［7］Morton，N.L.Pricing Risk Transfer Transactions［Z］.Porto Cervo:The 31th ASTIN Colloquium，2000.

［8］Wang，S.S.Cat Bond Pricing Using Probability Transforms［R］.Geneva Papers，2004.

［9］Christofides，S.，Smith，A.D.DFA － The Value of Risk［Z］.Meyers:CAS Forum，2001.

［10］Christofides，S.Pricing of Catastrophe Linked Securities ［Z］. Bergen: The 35th ASTIN Colloquium，2004.

［11］Egami，M.，Young，V.R.Indifference Prices of Structured Catastrophe(CAT)Bonds［J］.Insurance:Mathematics and Economics，2008，42(2):771－778.

［12］Jarrow，R.A.A Simple Robust Model for Cat Bond Valuation ［J］.Finance Research Letters，2010，7(2):72－79.

［13］Zhu，W.G.Ambiguity Aversion and an Intertemporal Equilibrium Model of Catastrophe－Linked Securities Pricing［J］.Insurance:Mathematics and Economics，2011，49(1):38－46.

［14］李永，范蓓，劉娟.多事件觸發巨災債券設計與定價研究:以中國臺風債券為例［J］.中國軟科學，2012，(3):41 －48.

［15］Vasicek，O.An Equilibrium Characterization of the Term Structure ［J］.The Journal of Financial Economics，1977，5(2):177 －188.

［16］Cox，J.C.，Ingersoll，J.E.，Ross，S.A.A Theory of the Term Structure of Interest Rates［J］.Econometrica，1985，53(2):385 －467.

［17］Chan，K.C.，Karolyi，A.G.，Longstaff，F A.，Sanders，A.B.An Empirical Comparison of Alternative Models of the Short－ Term Interest Rate［J］.The Journal of Financial Economics，1992，47(3):1209－1227.

［18］Poncet，P.，Vaugirard，V.E.The Pricing of Insurance Linked Securities under Interest Rate Uncertainty［J］.Journal of Risk Finance，2002，3(3):48 － 59.

［19］王銀成，王和，李秀芳，等.中國財產保險重大災因分析報告(2008)［M］.北京:中國財政經濟出版社，2009.

［20］康晗彬，邢天才.考慮多風險因素的我國巨災債券定價研究［J］.保險研究，2013，(8):94－106.

(責任編輯:韓淑麗)

F830.9

A

1000－176X(2014)05－0059－06*

2014－02－16

邢天才 (1961－)，男，山東青島人，教授，經濟學博士，博士生導師，主要從事金融市場監管、保險經濟與政

·金融與投資·