基于免疫進化細菌覓食算法的多目標無功優化

李 瑩，簡獻忠

(上海理工大學 電氣工程系，上海 2 00093)

基于免疫進化細菌覓食算法的多目標無功優化

李 瑩，簡獻忠

(上海理工大學 電氣工程系，上海 2 00093)

為了更好地解決電力系統多目標無功優化問題，分析了當前多目標無功優化算法存在的缺陷，提出了一種基于免疫進化的改進多目標細菌覓食優化算法。該算法求得的Pareto最優解分布均勻，收斂性和魯棒性好。IEEE14，IEEE30節點測試系統的算例結果表明所提的算法在多目標無功優化中具有良好的效果，為各目標之間的權衡分析提供了有效工具，是一種求解多目標無功優化問題的有效方法。

無功優化;多目標;免疫進化;細菌覓食優化算法;非支配排序

0 引言

當前隨著電力系統規模的不斷擴大，無功優化涉及的目標越來越多［1～3］，然而各個目標之間存在競爭關系，彼此矛盾。傳統的多目標無功優化方法將多目標問題轉化為單目標再求解［4～6］，這類方法存在明顯的缺點:每次計算彼此獨立，結果可能出現不一致的情況，且優化過程中考慮的各因素在總目標中所占權重的改變將影響整個目標系統無功的優化結果。因此，本文將基于精英選擇法的Pareto最優前沿［7］引入尋優機制中，利用非支配排序和擁擠距離排序對種群進行選擇更新，且輸出一組Pareto非支配解集［8］，為不同的應用場合及需求提供選擇。

目前應用于無功優化的智能算法很多，并取得了一些研究成果［9～11］，但是基于 Pareto最優前沿的多目標細菌覓食優化算法的研究文獻尚未見報道，因此，本文提出一種基于免疫進化的改進多目標細菌覓食優化算法 (IA－IBFO)，并將此算法應用于多目標無功優化問題，最終仿真結果表明，本文算法不僅能夠保持Pareto最優解的多樣性，同時還具有很好的收斂性能。

1 無功優化模型與Pareto最優解概念

1.1 多目標無功優化的數學模型

本文選擇系統有功網損最小為經濟性指標，電壓偏移量最小以及電壓安全穩定裕度最大為技術性指標，無功優化的多目標函數表達式如下［12］:

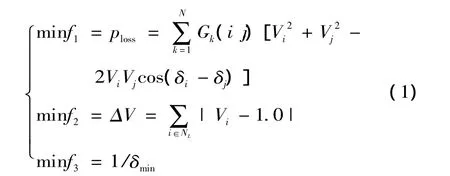
式中:f1為系統網損;f2為電壓偏差;f3為電壓穩定裕度;N為系統支路數;Gk(i，j)為線路k的電導;Vi，Vj，δi，δj為支路k兩端節點電壓幅值和相角;以系統收斂潮流雅可比矩陣的最小奇異值δmin作為系統靜態電壓穩定裕度的指標，為了使各目標函數具有統一的最小化形式，對δmin取倒數，將靜態電壓穩定裕度最大轉化為最小化函數形式。

1.2 等式約束

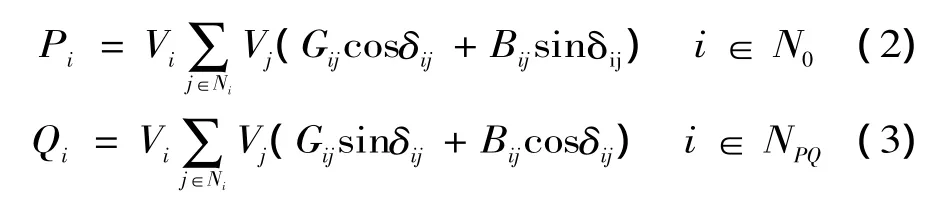
等式約束是指有功功率與無功功率保持平衡的條件，即功率平衡方程。式中:Pi，Qi分別為給定的節點i的有功和無功;Bij為節點i，j之間的電納值;N0為除平衡節點外的總節點數。

1.3 不等式約束

不等式約束條件指控制變量的約束條件與狀態變量的約束條件。

(1)控制變量約束

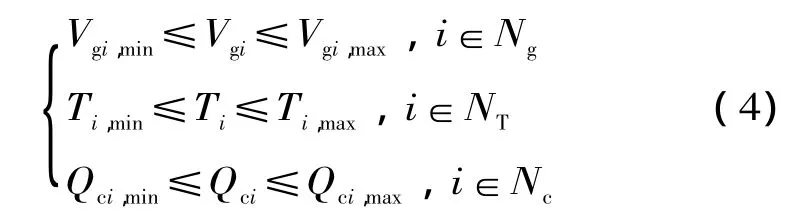
式中:Ng為可調發電機的節點數;NT為可調變壓器的節點數;Nc為無功補償裝置的節點數;Vgi為發電機的機端電壓;Ti為可調變壓器變比，Qci為無功補償裝置容量。

(2)狀態變量約束

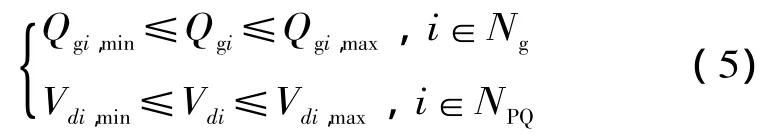
式中:Qgi為發電機無功出力;Vdi為PQ節點電壓。

1.4 Pareto最優解的基本概念

(1)Pareto支配關系。對于兩個決策變量u和v，且u∈S，v∈S，若滿足:

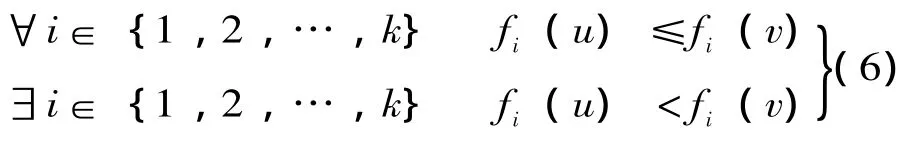
則稱決策變量u支配v，記為u?v。此時稱u為非支配的，v為被支配的。

(2)Pareto最優解。對于多目標優化問題的一個可行解x*∈S，當且僅當S中不存在x，使x?x*，即x*是可行域S的非支配個體，則稱x*為多目標優化問題的Pareto最優解，所有Pareto最優解構成Pareto最優解集，也就是全局最優解集。

2 基于免疫進化的改進多目標細菌覓食優化算法及其在無功優化中的應用

2.1 改進的細菌覓食算法

細菌覓食優化算法 (Bacterial Foraging Optimization，BFO)是Passina于2002年基于細菌覓食行為而提出的一種仿生隨機搜索算法［13］，該算法通過群體細菌之間的競爭和協作，實現搜索的優化，在BFO算法中，最核心的一個步驟就是趨化操作，趨化算子根據適應度調節游動方向，通過隨機游動來搜索全局最優解，從而確保了細菌的局部搜索能力，但由于細菌沒有充分利用其他細菌個體的信息，使得收斂速度較慢。為此，本文將賦予細菌以靈敏度來感知個體極值和全局極值的差異，使得細菌自適應調節游動步長，以適應環境。具體步驟改進如下:

(1)產生單位向量φ(i)，細菌執行翻轉操作。

(2)改善細菌種群位置。細菌個體按照靈敏度進行群游，當適應度不再增強時，則操作結束，靈敏度定義為:

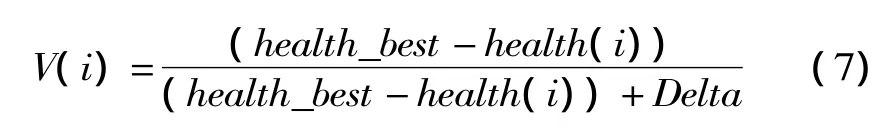
其中，health_best表示細菌種群歷史最好位置，health(i)表示第i個細菌當前位置，Delta定義為靈敏度算子，其大小由適應度函數的變化范圍決定，在此取值為6 000;式 (8)為細菌群游公式:

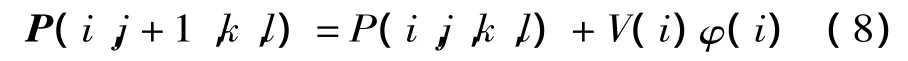
式中:P(i，j，k，l)表示第i個細菌的空間位置向量，其中j表示第j代趨化循環，k表示第k代繁殖循環，l表示第l代遷移循環;φ(i)表示群游選定的方向。

(3)將復制操作與驅散操作合并為以適應度作為判斷條件的驅散操作，設細菌個體的適應度為AdaptVi，菌群的平均適應度為MeanAdapt，如果AdaptVi＞MeanAdapt，則對該細菌個體執行驅散操作。由于多目標優化有多個優化指標可以作為適應度的判斷條件，本文選取如下方案作為適應度的判斷條件，去菌群的平均適應度為每個個體極值的平均值，即:

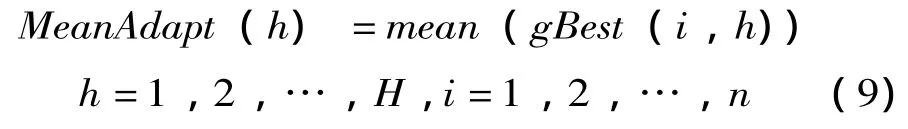
其中，H是目標函數的個數，n是菌群數目，mean(gBest(i，h))表示n個細菌個體極值的平均值。

2.2 應用于多目標無功優化的免疫細菌覓食算法

(1)初始群體的生存和編碼方式

本文編碼方案采用實數和整數混合的方式。控制變量中，PV節點發電機機端電壓采用實數編碼，并聯電容投運組數、有載調壓變壓器主接頭檔位為整數編碼。則控制變量編碼格式為:

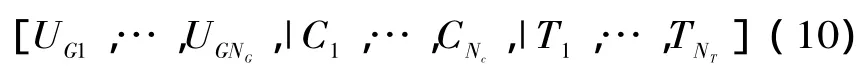
式中:UGi，Ci，Ti分別為某PV節點發電機機端電壓、并聯電容投運組和有載調壓變壓器主接頭檔位;NC，NT分別為PV節點并聯電容補償節點總數和有載調壓變壓器組數。

(2)非支配排序

在選擇運算之前，用擂臺賽法則構造非支配解集。其基本思路是:在每一輪比較時，從構造集中選出一個個體出任擂主，由擂主與構造集中其他個體進行比較，敗者被淘汰出局，勝者成為新的擂主，并繼續該輪比較。一輪比較后，最后的擂主個體即為非支配個體，將其保存在外部精英集中。該算法的時間復雜度優于改進的非支配遺傳算法［14］。

(3)擁擠度算子

為了保持個體的多樣性、防止個體在局部堆積，引入擁擠度距離這一概念。擁擠度是指種群中給定個體周圍的個體密度，計算步驟為:①對個體初始化距離，令L［i］d=0;②對個體按第m個目標函數值升序排列;③使得排序邊緣上的個體具有選擇優勢，給定一個大數L［0］d=L［l］d=M;④對排序中間的個體，求擁擠距離:L［i］d=L［i］d+(L［i+1］m－L［i－1］m)(L［i］m為第i個個體的第m目標函數);⑤對不同的目標函數，重復步驟②～④。

(4)選擇運算

選擇過程使優化朝著Pareto最優解的方向進行并使解均勻散布。經過排序，非支配個體已保存在精英集中，對精英集中的個體按照擁擠距離大小再次排序，取擁擠距離相對大的個體保留，即周圍較不擁擠的個體，淘汰掉擁擠距離較小的個體，這將使Pareto最優解集具有多樣性，并且均勻分布。

(5)精英集的克隆選擇

本文借鑒免疫算法中的克隆選擇思想［15］，并將其引入Pareto最優解集中，通過克隆、高頻變異和隨機交叉操作來增加Pareto最優解的多樣性，以及提高算法的收斂精度。

①在每代產生的非支配集中，選擇擁擠度距離大的粒子進行自我復制，產生克隆群體Nc。

②對Nc進行高頻變異，隨后進行隨機交叉，其中，高頻變異按照公式 (11)進行，β是高頻變異概率，按照公式 (12)計算，適應值越小的個體，變異的概率越大，搜索的空間越寬。其中fit為個體的適應值，m為目標函數的個數。

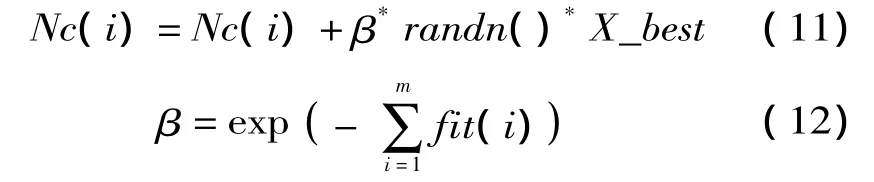
③對NC群體進行隨機交叉，產生s個粒子后代，作為免疫細胞注入Nc群體。交叉采用公式(13)進行，其中a，b，c，d為克隆群體的互不相同的隨機粒子。

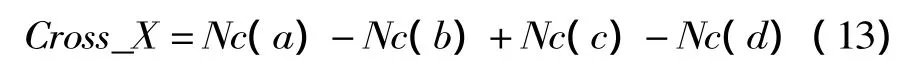
④采用免疫算法的克隆、變異、交叉策略形成Nc+s個新種群，對其適應值進行比較后產生非支配解集，該解集與當代非支配解集合并產生更新的Pareto最優解集，加入精英集中。

由步驟 (1)～(5)可得基于IA－IBFO的多目標無功優化流程圖如圖1所示。

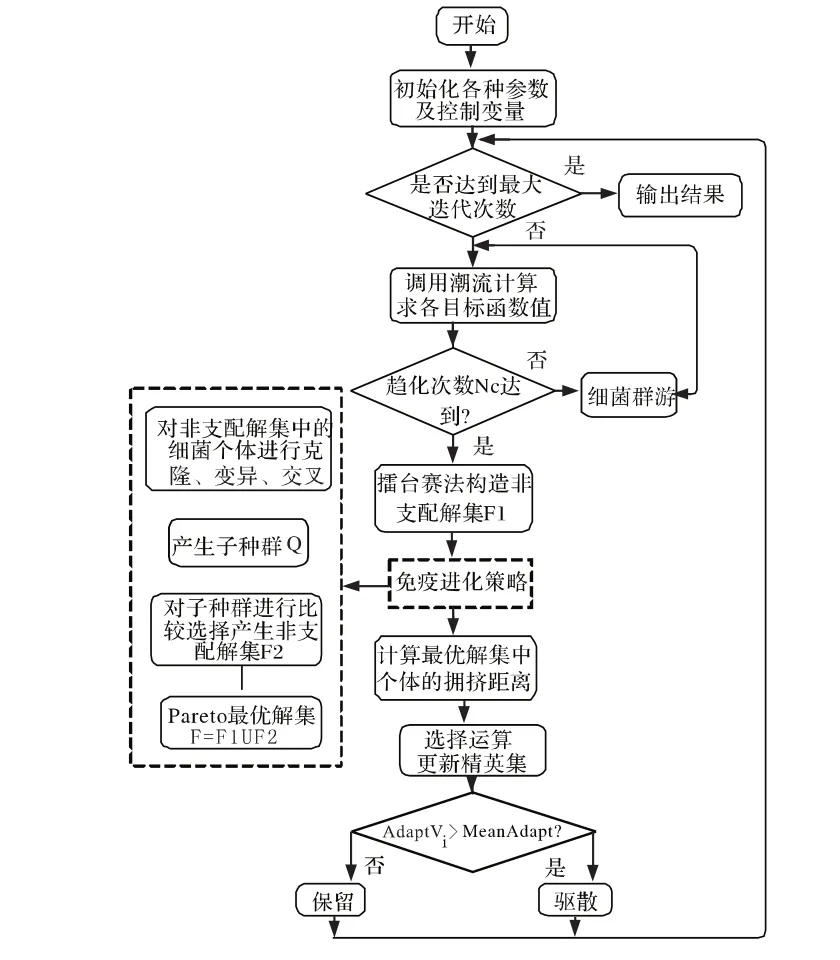
圖1 基于IA－IBFO算法的多目標無功優化流程

3 算例分析

本文使用Matlab進行無功優化仿真計算，分別對IEEE14節點和IEEE30節點系統進行仿真來驗證本文所提算法的優化效果。算法中相關的參數選取為:種群規模n=100，精英集規模F=20，迭代次數itermax=100。

3.1 IEEE14節點優化結果

IEEE14系統共有14個節點，20條支路，5臺發電機，3臺可調變壓器以及1個并聯補償電容器節點，系統節點參數和支路參數參見文獻［16］。為了便于分析說明，本算例只考慮有功網損和電壓穩定裕度兩個指標，仿真測試結果如圖2所示。

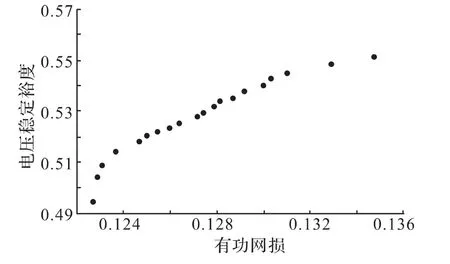
圖2 基于IA－IBFO算法的無功優化Pareto前沿

圖2顯示了某次計算求得的1組Pareto解的分布，從圖可以看出有功網損與電壓穩定裕度這兩個目標函數相互矛盾，最優解集分布均勻，具有較好的多樣性，能給用戶提供了多樣化的選擇。

表1給出了IA－IBFO算法與標準BFO算法分別運行30次無功優化所得最優解。

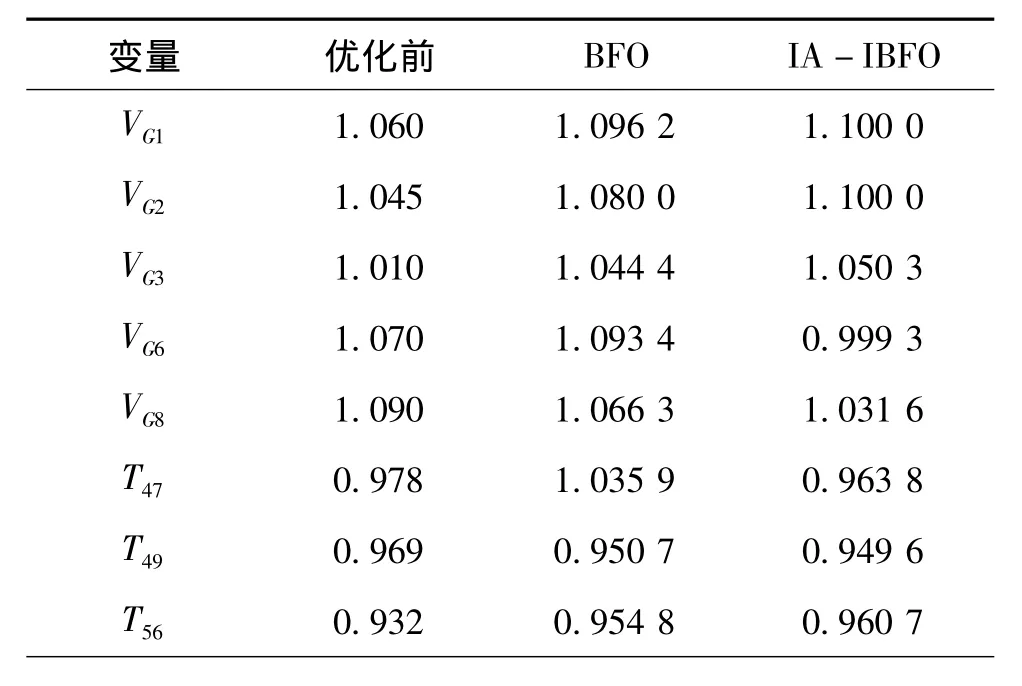
表1 不同算法優化結果比較

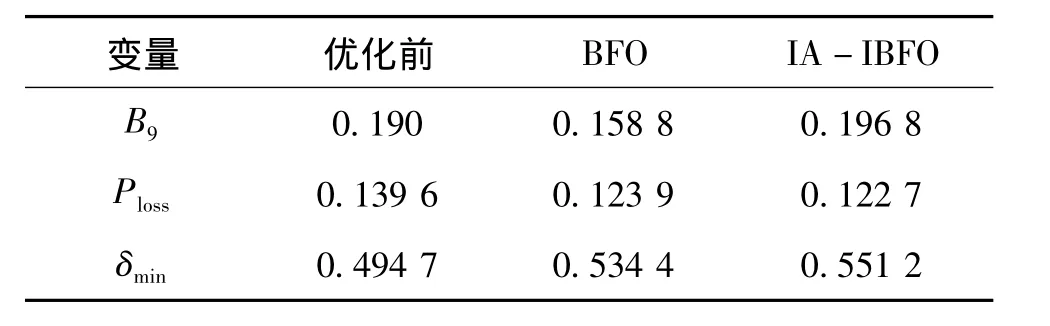
續表

由表1知，IA－IBFO優化后系統的網損降低12.11%，BFO優化后網損降低11.25%;IAIBFO優化后的電壓穩定裕度也優于BFO。由此可見，IA－IBFO算法在尋優過程中能更好地發現全局最優解。

IA－IBFO和BFO兩種算法的有功網損和電壓穩定裕度的收斂曲線圖分別如圖3、圖4所示，由圖可以看出本文所提算法無論在收斂速度上還是優化效果上都優于BFO。

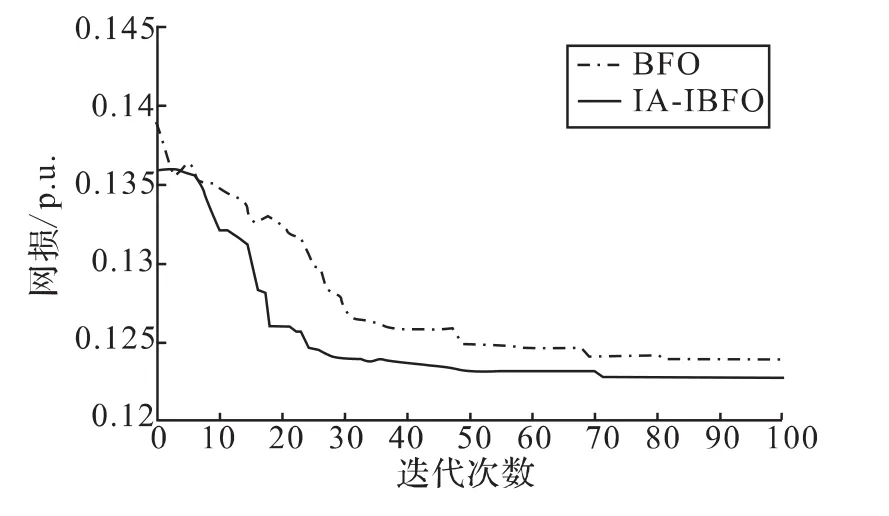
圖3 BFO和IA－IBFO的有功網損收斂特性曲線圖

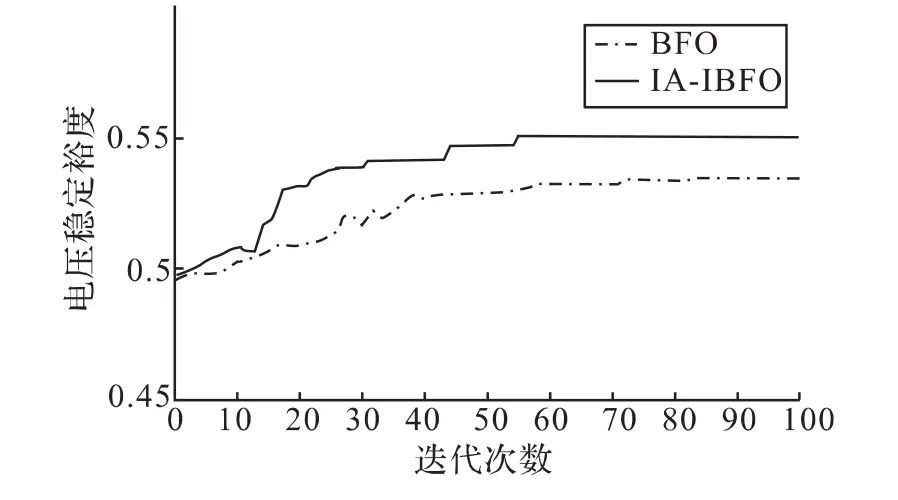
圖4 BFO和IA－IBFO的電壓穩定裕度收斂特性曲線圖

3.2 IEEE30節點優化結果

IEEE30系統共有30個節點，41條支路，6臺發電機，4臺可調變壓器以及2個并聯補償電容器節點，系統節點參數和支路參數參見文獻［15］。運用IA－IBFO算法對系統進行無功優化，仿真結果如圖5所示。由圖可以看出該算法無功優化所得Pareto最優前沿分布比較均勻，可以反映出IA－IBFO算法在尋優過程中能更好地保持種群多樣性，保證算法在全局區域能有更好的搜索能力。

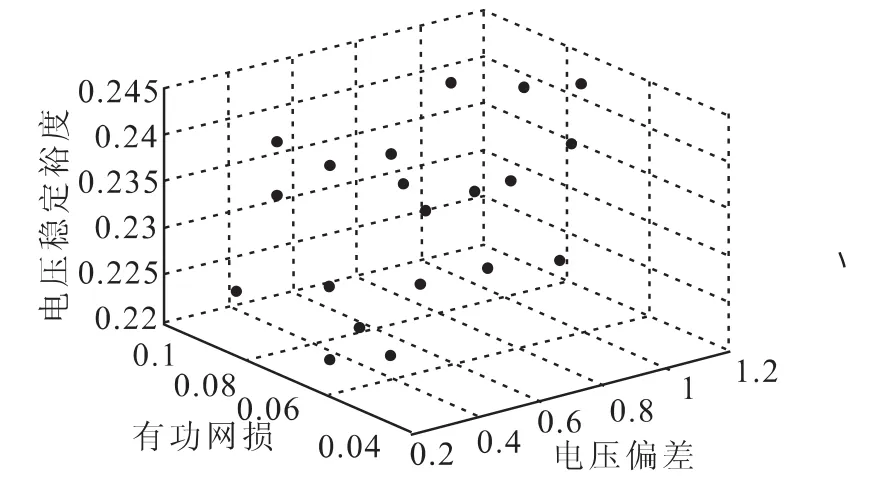
圖5 IA－IBFO的Pareto前沿

表2給出了IA－IBFO與BFO的性能對比，由IA－IBFO算法得到的有功網損，電壓偏差及電壓穩定裕度均優于BFO所得的結果。

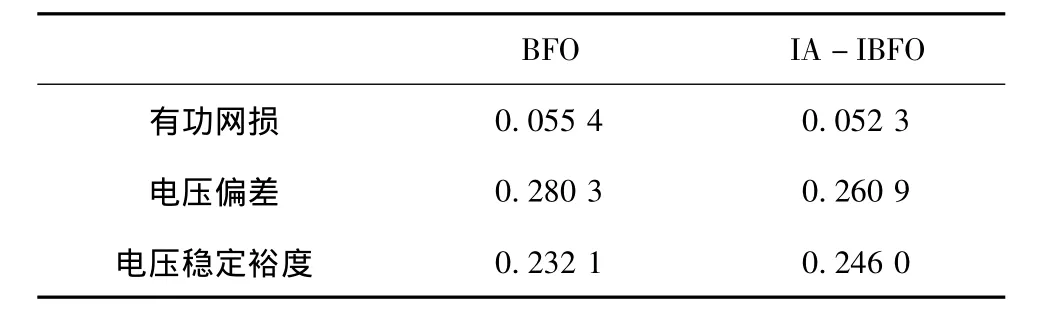
表2 不同算法優化結果比較

4 結論

本文提出一種基于免疫進化的改進多目標細菌覓食優化算法，并將其首次應用于多目標無功優化。仿真結果表明，該算法能較快地收斂到全局最優解，并且Pareto最優解集分布均勻，具有較好的多樣性，決策者可根據實際系統的要求進行最優解的選擇，避免了對多目標進行加權求解的盲目性，體現了多目標優化的工程實際意義，是一種求解多目標無功優化的好方法。當前隨著電力系統規模的擴大，無功優化時需要考慮的因素必將越來越多，如何進行電力市場下的無功優化的建模，國內外的學者正在積極探索，相信IA－IBFO可提供一個較好的算法支持。

［1］ Stephen D S，Somasundaram P．Solution for multi-objective reactive power optimization using fuzzy guided tabu search［J］．Arabian Journal for Science and Engineering，2012，37(8):2231-2241．

［2］ Rayudu K，Jayalaxmi A，Yesuratnam G，et al．Multi objective comparison of GA and LP techniques for generator reactive power optimization［C］．Power India Conference，2012 IEEE Fifth．IEEE，2012:1-5．

［3］ Singh H，Srivastava L．Multi-objective reactive power management using differential evolution［C］．Power Electronics(IICPE)，2012 IEEE 5th International Conference on．IEEE，2012:1-6．

［4］王玉榮，萬秋蘭，陳昊．基于模糊聚類和學習自動機的多目 標 無 功 優 化 ［J］．電 網 技 術，2012，36(7):224-230．

［5］陳得宇，張仁忠，沈繼紅，等．基于適應性權重遺傳算法的多目標無功優化研究［J］．電力系統保護與控制，2010，38(6):1-7．

［6］馬立新，王守征，呂新慧，等．電力系統無功優化的反向優化差分進化算法 ［J］．控制工程，2010，17(6):803-806．

［7］李鑫濱，朱慶軍．一種改進粒子群優化算法在多目標無功優化中的應用 ［J］．電工技術學報，2010，25(7):137-143．

［8］ Kalyanmoy Deb，Amrit Pratap，Sameer Agarwal，et al．A fast and elitist multi-objective genetic algorithm:NSGA-II［J］．Evolutionary Computation，IEEE Transactions on，2002，6(2):182-197．

［9］ Abido M A．A niched Pareto genetic algorithm for multiobjective environmental/economic dispatch［J］．International Journal of Electrical Power＆ Energy Systems，2003，25(2):97-105．

［10］李鴻鑫，李銀紅，李智歡．多目標進化算法求解無功優化問題的比較與評估 ［J］．電網技術，2013，37(6):1651-1658．

［11］ Zhang X，Chen W，Dai C，et al．Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization ［J］．International Journal of Electrical Power＆ Energy Systems，2010，32:351-357．

［12］李如琦，李芝榮，王維志，等．基于差分策略的多目標電力系統無功優化 ［J］．電網技術，2012，36(12):170-175．

［13］ Passina K M．Biomimicry of bacterial foraging for distributed optimization and control［J］．Control Systems Magazine，IEEE，2002，22(3):52-67．

［14］鄭金華，蔣浩，鄺達，等．用擂臺賽法則構造多目標Pareto最優解集的方法 ［J］．軟件學報，2007，6(18):1287-1297．

［15］Castro L N，Zuben F J．Artificial immune system:Part I:basic theory and applications［R］．Campinas，Brazil:State University of Campinas，School of Computing and E-lectrical Engineering，1999．

［16］張伯明，陳壽孫，嚴正．高等電力網絡分析 ［M］．(第2版)．北京:清華大學出版社，2007．

Bacterial Foraging Optimization Algorithm Based on Immune Algorithm for Multi-Objective Reactive Power Optimization

Li Ying，Jian Xianzhong
(Department of Electrical Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China)

In order to solve the problem of multi-objective reactive power optimization，firstly the defects of current algorithms are analyzed，then an improved multi-objective bacterial foraging optimization algorithm based on immune algorithm technique is proposed．It can obtain uniformly distributed Pareto-optimal solutions and has good convergence and excellent robustness．Finally this method is applied to IEEE14-bus and IEEE30-bus testing system．The results show that the proposed method can obtain good results for multi-objective reactive power optimization，which provides an effective tool for measuring the performance of different objective functions．Thus it should be a new method for multi-objective reactive power optimization in power systems．

reactive power optimization;multi-objective;immune algorithm;bacterial foraging optimization algorithm;non-dominated sorting

TM714.3;TP301.6

A

10.3969/j.issn.1672-0792.2014.04.002

2013－11－28。

上海市自然科學基金資助項目 (12ZR1420800)。

李瑩 (1987-)，女，碩士研究生，研究方向為電能質量優化與分析，E-mail:727145259@qq．com。