動(dòng)態(tài)S盒的密碼性質(zhì)*

申 兵,霍家佳

(1.保密通信重點(diǎn)實(shí)驗(yàn)室,四川成都610041;2.中國(guó)電子科技集團(tuán)公司第三十研究所,四川成都610041)

動(dòng)態(tài)S盒的密碼性質(zhì)*

申 兵1,霍家佳2

(1.保密通信重點(diǎn)實(shí)驗(yàn)室,四川成都610041;2.中國(guó)電子科技集團(tuán)公司第三十研究所,四川成都610041)

劉國(guó)強(qiáng)和金晨輝給出了動(dòng)態(tài)S盒差分概率的定義,分析了其不可能差分的特性、最大差分概率的上界及可達(dá)性,這是首個(gè)從動(dòng)態(tài)S盒的概念和性質(zhì)方面的研究。沿著這個(gè)方向,本文給出動(dòng)態(tài)線性概率、動(dòng)態(tài)非線性度、動(dòng)態(tài)代數(shù)次數(shù)、動(dòng)態(tài)代數(shù)免疫階等定義,分析了這些動(dòng)態(tài)性能指標(biāo)的界及可達(dá)性,并用仿真模擬的方法驗(yàn)證了定義的合理性和定理的正確性,同時(shí)還分析了動(dòng)態(tài)S盒的性能隨規(guī)模變化的規(guī)律。

動(dòng)態(tài)S盒 動(dòng)態(tài)差分概率 動(dòng)態(tài)線性概率 動(dòng)態(tài)非線性度 動(dòng)態(tài)代數(shù)次數(shù) 動(dòng)態(tài)代數(shù)免疫階

0 引 言

S盒(Substitution Box)是在密碼算法設(shè)計(jì)中廣泛使用的一類非線性部件,能夠?yàn)樗惴ㄌ峁┖玫姆蔷€性性,并具有良好的數(shù)學(xué)模型和較系統(tǒng)的評(píng)價(jià)指標(biāo),理論基礎(chǔ)較為完善,但研究成果較少,存在一定的研究難度。

S盒首次出現(xiàn)在Lucife算法中,隨后因DES的使用而廣為流行。如DES使用8個(gè)6入4出S盒, AES、SMS4、Camellia使用有限域GF(28)上乘法求逆變換構(gòu)造的S盒,MARS使用隨機(jī)產(chǎn)生的8入32出S盒,序列密碼RC4則完全依賴于一個(gè)隨時(shí)間變化的8入8出S盒。

S盒的使用模式大致分為兩類,一類是靜態(tài)使用,即S盒在算法中始終保持不變,如前面提到的

AES、SMS4、Camellia、MARS等,另一類是動(dòng)態(tài)使用,即在算法中動(dòng)態(tài)可變,如RC4每運(yùn)行一拍,S盒的某兩個(gè)位置的值交換一次,還有一些分組密碼算法使用與密鑰相關(guān)的S盒,密鑰每變化一次,S盒動(dòng)態(tài)改變一次,如Khufu,Blowfish,Twofish,PRINTcipher。

算法中動(dòng)態(tài)使用S盒的主要目的是提高算法的安全性,1995年,E.Biham提出一種使用密鑰相關(guān)S盒的方法來(lái)改進(jìn)DES[1],分析表明改進(jìn)后的DES在抗差分密碼分析和線性密碼分析的性能上有所提升,作者在文中寫道:

“只有在知道S盒的內(nèi)容的前提下,線性攻擊和差分攻擊才可以實(shí)施,如果S盒依賴于密鑰,且通過(guò)強(qiáng)有力的密碼方法選取,則線性攻擊和差分攻擊會(huì)更困難”。

Khufu的S盒本身是秘密的,從密鑰擴(kuò)展得來(lái),每8輪使用一個(gè),即第一個(gè)8輪使用第一個(gè)S盒,第二個(gè)8輪使用第二個(gè)S盒,以此類推。由于Khufu有一個(gè)與密鑰相關(guān)的秘密S盒,它對(duì)抗差分密碼分析起到很重要的作用,對(duì)16輪最好的攻擊需要243個(gè)選擇明文和243次操作[2]。

Twofish的密鑰相關(guān)S盒是這樣構(gòu)造的,使用兩個(gè)8入8出固定S盒q0和q1,以及密鑰,構(gòu)造4個(gè)密鑰相關(guān)S盒,首先對(duì)密鑰作一個(gè)線性變換,得到k個(gè)32比特?cái)?shù)據(jù)L0,L1,…,Lk-1,其中k根據(jù)密鑰長(zhǎng)度可以取2,3,4。對(duì)32比特輸入X,將其分為4個(gè)字節(jié),每個(gè)字節(jié)查兩個(gè)固定S盒中的一個(gè),然后異或密鑰數(shù)據(jù),重復(fù)上述步驟至少k次,再查一次固定S盒,得到32比特輸出Y。如圖1所示。

圖1 Twofish密鑰相關(guān)S盒構(gòu)造示意Fig.1 Construction key related S-box of Twofish

作者在其設(shè)計(jì)文檔中聲稱,設(shè)計(jì)密鑰相關(guān)的動(dòng)態(tài)S盒的目的是為了抗差分攻擊、高階差分攻擊、線性攻擊、相關(guān)密鑰攻擊,而且,如果動(dòng)態(tài)S盒設(shè)計(jì)得當(dāng),這樣做是有效的。

動(dòng)態(tài)S盒的研究方向包括產(chǎn)生方法、密碼學(xué)性質(zhì)研究、以及在算法中的使用模式等。文獻(xiàn)[3]研究了隨機(jī)產(chǎn)生S盒的密碼學(xué)性質(zhì),并給出了一種構(gòu)造依賴于密鑰的隨機(jī)S盒的產(chǎn)生方法。文獻(xiàn)[4]研究了隨機(jī)交換S盒的兩個(gè)位置上的值后密碼學(xué)性質(zhì)的變化特征。文獻(xiàn)[5]則針對(duì)有限域上求逆變換構(gòu)造的S盒,給出了交換位置后差分概率不降低的條件,并給出了具體的構(gòu)造方法。

文獻(xiàn)[6]則針對(duì)有限域上求逆與仿射變換復(fù)合得到的動(dòng)態(tài)S盒進(jìn)行研究,給出了動(dòng)態(tài)S盒差分概率的刻畫(huà)方法,分析了其不可能差分的特性、最大差分概率的上界及可達(dá)性。這是首個(gè)從動(dòng)態(tài)S盒的概念和性質(zhì)方面的研究。本文將沿著這個(gè)思路,給出一般意義下動(dòng)態(tài)S盒的密碼學(xué)性質(zhì)的定義,并給出了動(dòng)態(tài)S盒密碼性質(zhì)的界及可達(dá)性。

本文的第1節(jié)給出動(dòng)態(tài)S盒的相關(guān)定義,第2節(jié)給出已有的結(jié)果,第3節(jié)給出并證明動(dòng)態(tài)密碼性質(zhì)的界及可達(dá)性,第4節(jié)為仿真實(shí)驗(yàn),第5節(jié)為結(jié)論。

1 動(dòng)態(tài)S盒的相關(guān)定義

設(shè)S:{0,1}n→{0,1}n為n比特S盒,An為{0, 1}n→{0,1}上的仿射布爾函數(shù)集,x·y表示x和y的內(nèi)積,wb(f(x))表示布爾函數(shù)f(x)的漢明重量,即f(x)值域中1的個(gè)數(shù)。用d(f(x),g(x))表示兩個(gè)布爾函數(shù)f(x)和g(x)的距離,即d(f(x),g(x)) =wb(f(x)⊕g(x))。

記E(·)為數(shù)學(xué)期望,用#{X}表示集合X的元素個(gè)數(shù),當(dāng)S的輸入差分為α,輸出差分為β的差分概率表示為

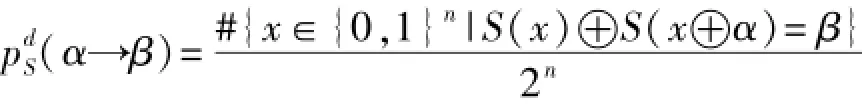
當(dāng)S的輸入掩蓋值為a,輸出掩蓋值為b的線性概率表示為

文獻(xiàn)[6]給出了動(dòng)態(tài)S盒及其差分概率的定義,如下:

定義1(動(dòng)態(tài)S盒)[6]設(shè):Si:{0,1}n→{0,1}n,i∈{0,1,…,m-1},則稱{Si}為動(dòng)態(tài)S盒,并稱動(dòng)態(tài)S盒由S0,S1,…,Sm-1構(gòu)成。

不失一般性,本文總假設(shè)控制參數(shù)服從均勻

分布。

定義2(動(dòng)態(tài)S盒的差分概率)[6]設(shè):Si:{0,1}n→{0,1}n,i∈{0,1,…,m-1},α,β∈{0,1}n,則稱(α→β)=E((α→β)=(α→β)為動(dòng)態(tài)S盒{S}i的差分對(duì)應(yīng)α→β的差分概率。稱為maxα≠0,β((α→β))動(dòng)態(tài)S盒的最大差分概率。

類似地,我們給出動(dòng)態(tài)線性概率、動(dòng)態(tài)非線性度、動(dòng)態(tài)代數(shù)次數(shù)、以及動(dòng)態(tài)代數(shù)免疫階的定義:

定義3 設(shè)Si:{0,1}n→{0,1}n,i∈{0,1,…,m-1},a,b∈{0,1}n,則:

(2)給定l(x)∈An,

表示Si和l的距離。稱

(3)設(shè)deg(Si)為Si的代數(shù)次數(shù),則稱

(4)稱

從定義可以看出,當(dāng)m=1時(shí),定義2和定義3即為S盒的密碼性質(zhì)在通常意義下的定義。

2 已有的結(jié)果

關(guān)于單個(gè)S盒的密碼學(xué)性質(zhì),已得到深入的研究,關(guān)于其理論界,已有以下已知的結(jié)果:

定理1設(shè)S為一個(gè)n入n出S盒,則:

(1)非線性度nl(S)≤2n-1-.

(2)差分概率≥21-n.

(3)線性概率≥2-n.

(4)代數(shù)次數(shù)deg(S)≤n.

(5)代數(shù)免疫階AI(S)≤

.

在產(chǎn)生S盒時(shí),應(yīng)使各項(xiàng)指標(biāo)達(dá)到或者盡可能地接近上述的界。

文獻(xiàn)[6]則針對(duì)有限域上求逆與仿射變換復(fù)合得到的動(dòng)態(tài)S盒進(jìn)行研究,有以下結(jié)果:

定理2設(shè)n為偶數(shù),動(dòng)態(tài)S盒由GF(2n)的乘法逆變換及[GF(2)]n上的m個(gè)仿射變換Li(x)=Aix⊕ai的復(fù)合構(gòu)成,且任意的β∈GF(2n){0},對(duì)1≤i≠j≤m均成立,則動(dòng)態(tài)S盒的差分概率≤21-n(m+1)/m.

定理3設(shè)n為偶數(shù),m＜n,動(dòng)態(tài)S盒由GF(2n)的乘法逆變換x-1及GF(2n)上的m個(gè)一次可逆函數(shù)Li(x)=aix⊕bi構(gòu)成且a1,a2,…,am互不相同,α,β∈GF(2n){0}。則動(dòng)態(tài)S盒的差分對(duì)應(yīng)α→β的差分概率為21-n(m+1)/m,當(dāng)且僅當(dāng)存在1≤j≤m使得α×β=ai,且對(duì)1≤j≤m均有TrGF(2n)(×aj)=0。

文獻(xiàn)[6]只對(duì)特殊類型的動(dòng)態(tài)S盒的差分概率做了研究,實(shí)際上可以容易地將它推廣到一般的S盒,下面各節(jié)是相關(guān)的結(jié)果。

3 動(dòng)態(tài)S盒的密碼性質(zhì)及其構(gòu)造準(zhǔn)則

文獻(xiàn)[1]給出了AES的S盒在仿射動(dòng)態(tài)變換下的密碼學(xué)性質(zhì),這種仿射動(dòng)態(tài)變化的數(shù)量有限,不能滿足實(shí)際的需求。這里我們給出一般意義下的動(dòng)態(tài)S盒的密碼學(xué)性質(zhì)。

定理4 設(shè){S0,S1,…,Sm-1}為動(dòng)態(tài)S盒,且對(duì)每一個(gè)i∈{0,1,…,m-1}有:

(3)nl(Si)=n.

(4)deg(Si)=d.

(5)AI(Si)=a.

則動(dòng)態(tài)S盒的相應(yīng)密碼性質(zhì)也滿足這些界,即:

對(duì)應(yīng)α→β,使得對(duì)每一個(gè)i∈{0,1,…,m-1},有(α→β)=p.

(2)≤q.而且,plS=q當(dāng)且僅當(dāng)存在一對(duì)線性近似a→b,使得對(duì)每一個(gè)i∈{0,1,…,m-1},有

(a→b)=q.

(3)nl(S)≥n.而且,nl(S)=n當(dāng)且僅當(dāng)存在l∈An,使得對(duì)每一個(gè)i∈{0,1,…,m-1},有d(Si,l) =n.

(4)deg(S)=d.

(5)AI(S)≥a.而且,AI(S)=a當(dāng)且僅當(dāng)存在一個(gè)多項(xiàng)式函數(shù)P(X,Y),使得對(duì)每一個(gè)i∈{0,1,…,m-1},在Y=Si(X)且P(X,Y)=0的條件下,deg(P(X,Y))=a.

從定義2和定義3出發(fā)可以很容易地證明定理4,這里不再贅述。

由定理4,在產(chǎn)生動(dòng)態(tài)S盒時(shí),其中單個(gè)的S盒要滿足一定密碼學(xué)指標(biāo)外,作為一個(gè)整體的動(dòng)態(tài)S盒還要滿足一定的動(dòng)態(tài)性質(zhì),主要有:

(1)動(dòng)態(tài)差分概率盡可能小。

(2)動(dòng)態(tài)線性概率盡可能小。

(3)動(dòng)態(tài)非線性度盡可能大。

(4)動(dòng)態(tài)代數(shù)次數(shù)盡可能大。

(5)動(dòng)態(tài)代數(shù)免疫階盡可能大。

4 模擬實(shí)驗(yàn)

本節(jié)利用模擬實(shí)驗(yàn)驗(yàn)證定義3的合理性以及定理4的正確性,首先隨機(jī)產(chǎn)生256個(gè)8入8出的S盒,對(duì)每一個(gè)i=1,2,…,256,滿足:

(1)≤2-4.

(2)≤2-4.

(3)nl(S)≤96.

(4)deg(Si)=7.然后按照定義3測(cè)試它們的動(dòng)態(tài)差分概率、動(dòng)態(tài)線性概率、動(dòng)態(tài)非線性度、和動(dòng)態(tài)代數(shù)次數(shù),結(jié)果為:

(1)=2-7.5.

(2)=2-8.1.

(3)nl(Si)=104.7.

(4)deg(Si)=7.

由此驗(yàn)證了定義3和定理4的合理性和正確性,也可以看出,動(dòng)態(tài)S盒的密碼學(xué)性能比單個(gè)的S盒的性能要好,甚至超過(guò)了單個(gè)S盒的理論界。

動(dòng)態(tài)S盒的個(gè)數(shù)取多少合適?很難有一個(gè)理論的量化結(jié)論,這里仍然通過(guò)模擬的方法研究動(dòng)態(tài)S盒的密碼學(xué)性能隨著個(gè)數(shù)變化的規(guī)律。隨機(jī)產(chǎn)生m個(gè)S盒,每個(gè)S盒滿足上述4個(gè)條件,然后測(cè)試其動(dòng)態(tài)密碼學(xué)性能,結(jié)果如表1所示。

表1 隨機(jī)動(dòng)態(tài)S盒單個(gè)密碼性能比較表Table 1 Comparison of the single cryptographic property of random dynamic S-box

從表1可以看出,動(dòng)態(tài)S盒的代數(shù)次數(shù)不會(huì)隨著m的變化而變化,動(dòng)態(tài)非線性度、隨著m增大而增大,但增加的速度比較慢,動(dòng)態(tài)差分概率和動(dòng)態(tài)線性概率隨m的增大而增大,且增加的速度比較快。所以,動(dòng)態(tài)S盒對(duì)提升差分和線性性能的優(yōu)勢(shì)明顯,對(duì)提升非線性度的優(yōu)勢(shì)一般,對(duì)提升代數(shù)次數(shù)沒(méi)有作用。如果只滿足差分和線性性能,m取8就夠了,若還考慮到非線性度,m應(yīng)該取得比較大,但這也會(huì)增加實(shí)現(xiàn)的資源耗費(fèi),所以在實(shí)際中最好折衷考慮。

下面對(duì)每個(gè)S盒的密碼性質(zhì)不作限制的條件下隨機(jī)產(chǎn)生S盒,考察它們的動(dòng)態(tài)性質(zhì)。首先隨機(jī)產(chǎn)生256個(gè)隨機(jī)S盒,然后按照定義3測(cè)試它們的動(dòng)態(tài)差分概率、動(dòng)態(tài)線性概率、動(dòng)態(tài)非線性度、和動(dòng)態(tài)代數(shù)次數(shù),結(jié)果為:

(1)=2-6.95.

(2)=2-8.0.

(3)nl(Si)=104.7.

(4)deg(Si)=6.99.

比較這兩種產(chǎn)生隨機(jī)S盒的方法對(duì)動(dòng)態(tài)性能的影響,可以看出,限定單個(gè)S盒的指標(biāo)與不限定,其動(dòng)態(tài)性能的差別并不大,后者只是稍微弱了一點(diǎn)點(diǎn),但由于不限定指標(biāo)產(chǎn)生S盒不需要測(cè)試,從而節(jié)省了不少計(jì)算資源和時(shí)間,所以,在某些資源受限且需要在線產(chǎn)生S盒的場(chǎng)合,完全可以用后一種方式。

下面同樣測(cè)試動(dòng)態(tài)性質(zhì)隨規(guī)模變化的規(guī)律,如表2所示。

表2 隨機(jī)動(dòng)態(tài)S盒多個(gè)S盒指標(biāo)的密碼性能比較表Table 2 Comparison ofmulti-cryptographic properties of randomdynamic S-box

從表2也同樣可以看出,除了代數(shù)次數(shù)外,規(guī)模越大,動(dòng)態(tài)性能越好,動(dòng)態(tài)代數(shù)次數(shù)例外的原因是只要有一個(gè)差一點(diǎn),動(dòng)態(tài)性能就要下降,m越小,取到小于7的概率越小,所以表中前三個(gè)都是7而后面卻小于7,也可以看出當(dāng)m取到較大,性能也趨于穩(wěn)定且也有逐漸變好的趨勢(shì)。

5 結(jié) 語(yǔ)

本文在文獻(xiàn)[6]的基礎(chǔ)上,給出了動(dòng)態(tài)S盒的動(dòng)態(tài)差分概率、動(dòng)態(tài)線性概率、動(dòng)態(tài)非線性度、動(dòng)態(tài)代數(shù)次數(shù)、以及動(dòng)態(tài)代數(shù)免疫階的定義,在給定單個(gè)

S盒的這些指標(biāo)的前提下,給出了對(duì)應(yīng)動(dòng)態(tài)性能的界,并用模擬的方法驗(yàn)證了定義的合理性和定理的正確性,同時(shí)還分析了動(dòng)態(tài)S盒的性能隨規(guī)模變化的規(guī)律,對(duì)實(shí)際的動(dòng)態(tài)算法設(shè)計(jì)有重要的指導(dǎo)作用。如何利用這些性能分析動(dòng)態(tài)密碼算法的安全性,以及如何快速在線產(chǎn)生S盒等問(wèn)題,是未來(lái)研究的方向。

[1] BIHAM E.and BIRYUKOV A..How to Strengthen DES using Existing Hardware[C]//Advances in Cryptology-ASIACRYPT'94,Springer-Verlag,1995.

[2] H.GILLBERT and P.CHAUVAUD.A Chosen Plaintext Attack of the 16-Round Khufu Cryptosystem[C]//Advances in Cryptology-CRYPTO'94,Springer-Verlag, 1994:259-268.

[3] LIAM Keliher.Substitution Permutation Network Cryptosystems Using Key Dependent S-Boxes[D].Kingston, Ontario,Canada:Queen's University,1997.

[4] YU Yuyin.Wang Mingsheng,Li Yongqiang.Constructing differentially 4 uniform functions from known ones[J].Chinese Journal of Electronics,2013,22(3):495-499.

[5] QU Longjiang,Tan Yin,Tan Chikhow,Li Chao.Constructing Differentially 4-Uniform Permutations Over via the Switching Method[J].IEEE Transactions on Information Theory.2013,59(7),4675-4686.

[6] 劉國(guó)強(qiáng),金晨輝.一類動(dòng)態(tài)S盒的構(gòu)造與差分性質(zhì)研究[J].電子與信息學(xué)報(bào),2014,36(1):74-81.

LIU Guo-qiang,JIN Chen-hui,Investigation on Construction and Differential Property of a Classof Dynamic S-box [J],Journal of Electronics&Information Technology. 2014,36(1):74-81.

申 兵(1971—),男,碩士,高級(jí)工程師,主要研究方向?yàn)樾畔踩c通信保密;

SHEN Bing(1971—),male,M.Sci.,senior engineer,mainly engaged in information security and communications privacy.

霍家佳(1978—),女,碩士,高級(jí)工程師,主要研究方向?yàn)樾畔踩c通信保密。

HUO Jia-jia(1978—),female,M.Sci.,senior engineer,mainly engaged in information security and communications privacy.

Cryptographic Property of Dynam ic S-box

SHEN Bing1,HUO Jia-jia2
(1.Science and Technology on Communication Security Laboratory,Chengdu Sichuan 610041,China;
2.No.30 Institute of CETC,Chengdu Sichuan 610041,China)

LIU Guo-qiang and JIN Chen-huigives the definition of differential probability for dynamic S-box,analyze the charicteristics of impossible difference and the upper-bound and accessibility ofmaximum differential probability for dynamic S-box.This is the first try on the research of dynamic S-box's definition and properties.In lightof this,the definitions of dynamic linear probability,dynamic nonlinearity,dynamic algebraic degree and dynamic algebraic immunity are proposed,and the bounds of these cryptographic criterions and the accessibility of these bounds analyzed.Simulation experiments verify the rationality and validity of the definitions.Meanwhile,the rule of dynamic property with the change of dynamic S-box's size is also given.

dynamic S-box;dynamic differential probability;dynamic linear probability;dynamic nonlinearity;dynamic algebraic degree;dynamic algebraic immunity

TN918.1

A

1002-0802(2014)12-1429-05

10.3969/j.issn.1002-0802.2014.12.017

2014-09-02;

2014-11-12 Received date：2014-09-02;Revised date：2014-11-12

國(guó)家自然科學(xué)基金(No.61309034)資助;四川省科技廳杰出青年基金項(xiàng)目(2014JQ0055)資助

Foundation Item:National Natural Science Foundation of China(No.61309034);Outstanding Youth Foundation of the Science and Technology Department in Sichuan Province(2014JQ0055)