中國建筑業總產值的多元線性回歸分析

陳 于，彭 川

(1.重慶交通大學，重慶 400074;2.重慶理工大學，重慶 400054)

一、引言

在一定時期內完成的、以價值為表現形式的建筑業總產值，是反映建筑業生產規模、發展速度、經營效果等建筑業生產成果的綜合指標，也是國家制定經濟建設計劃的依據。為了更好地了解和更準確地統計建筑業總產值。本文將在參與建筑業的企業類型視角下，運用多元線性回歸方法，對影響建筑業總產值的企業類型進行多元線性回歸分析。

二、模型

(一)多元線性回歸理論

根據《計量經濟學》(第3版)［1］中對多元線性回歸的描述可知，多元線性回歸模型中總體回歸函數的隨機表達式為:

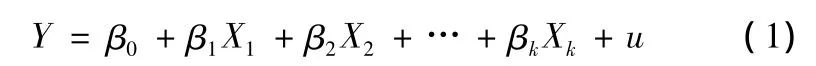
其中:Y表示因變量或被解釋變量;Xi表示自變量或解釋變量(i=1，2，…，k);k表示因變量的個數;βi表示回歸系數，是指Xi(i=1，2，…，k)的單位變化對Y值的“直接”或“凈”影響(i=1，2，…，k);u表示隨機干擾項。如果給出總體中的一個樣本觀測值:

估計出該樣本的回歸函數，它可以近似代表未知的總體回歸函數，其一般表達式為:

隨機表達式為:

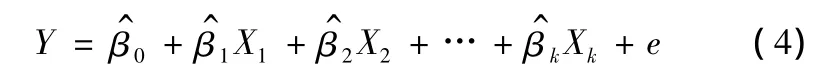
其中:e表示殘差或剩余項，可看成是總體回歸函數中的隨機干擾項u的近似代替。

在一個容量為n的樣本下，樣本回歸函數可表示為:

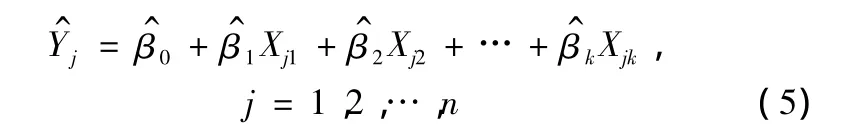
隨機表達式為:

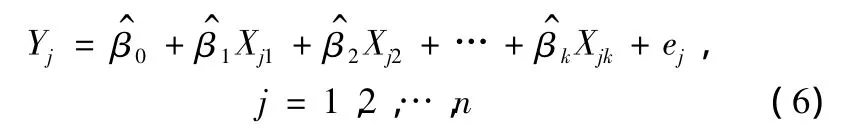
(二)建筑業總產值多元線性回歸模型

《中國統計年鑒》(2013)［2］中對建筑業總產值劃分為五大類:一是國有企業，二是集體企業，三是港澳臺商投資企業，四是外商投資企業，五是其他。為了方便對中國建筑業總產值的影響因素進行多元線性回歸分析，對數據進行如下處理:

(1)將建筑業總產值總計設定為因變量Y

(2)將國有企業設定為自變量X1

(3)將集體企業設定為自變量X2

(4)將港澳臺商投資企業設定為自變量X3

(5)將外商投資企業設定為自變量X4

(6)將其他設定為自變量X5

(7)多元線性回歸函數的隨機擾動項為u

(8)常數項和因變量X1、X2、X3、X4、X5的回歸系數為β0，β1，β2，β3，β4，β5

根據多元線性回歸理論，結合上述假定可以得到一個建筑業總產值的多元線性回歸表達式如下:

通過樣本估計得到總體回歸函數的近似表達式，也就是樣本回歸函數表達式為:

隨機表達式為:

三、算例

(一)算例概況

《中國統計年鑒》(2013版)中對建筑業總產值的描述如表1所示。

(二)計算過程

運用Eviews6軟件對表1中的數據進行多元線性回歸分析，得到的“make equation”計算結果如表2所示。

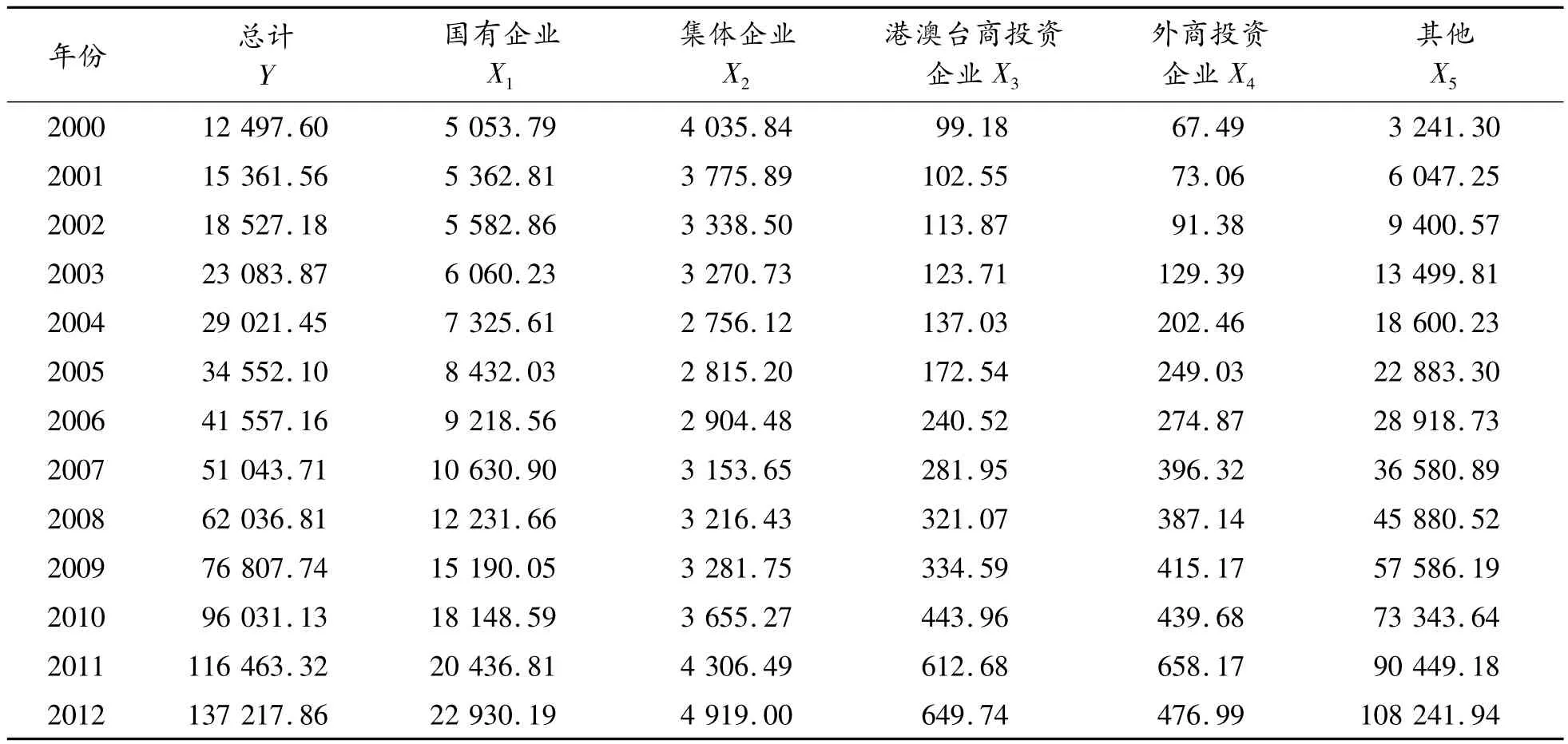
表1 中國建筑業總產值一覽表 億元

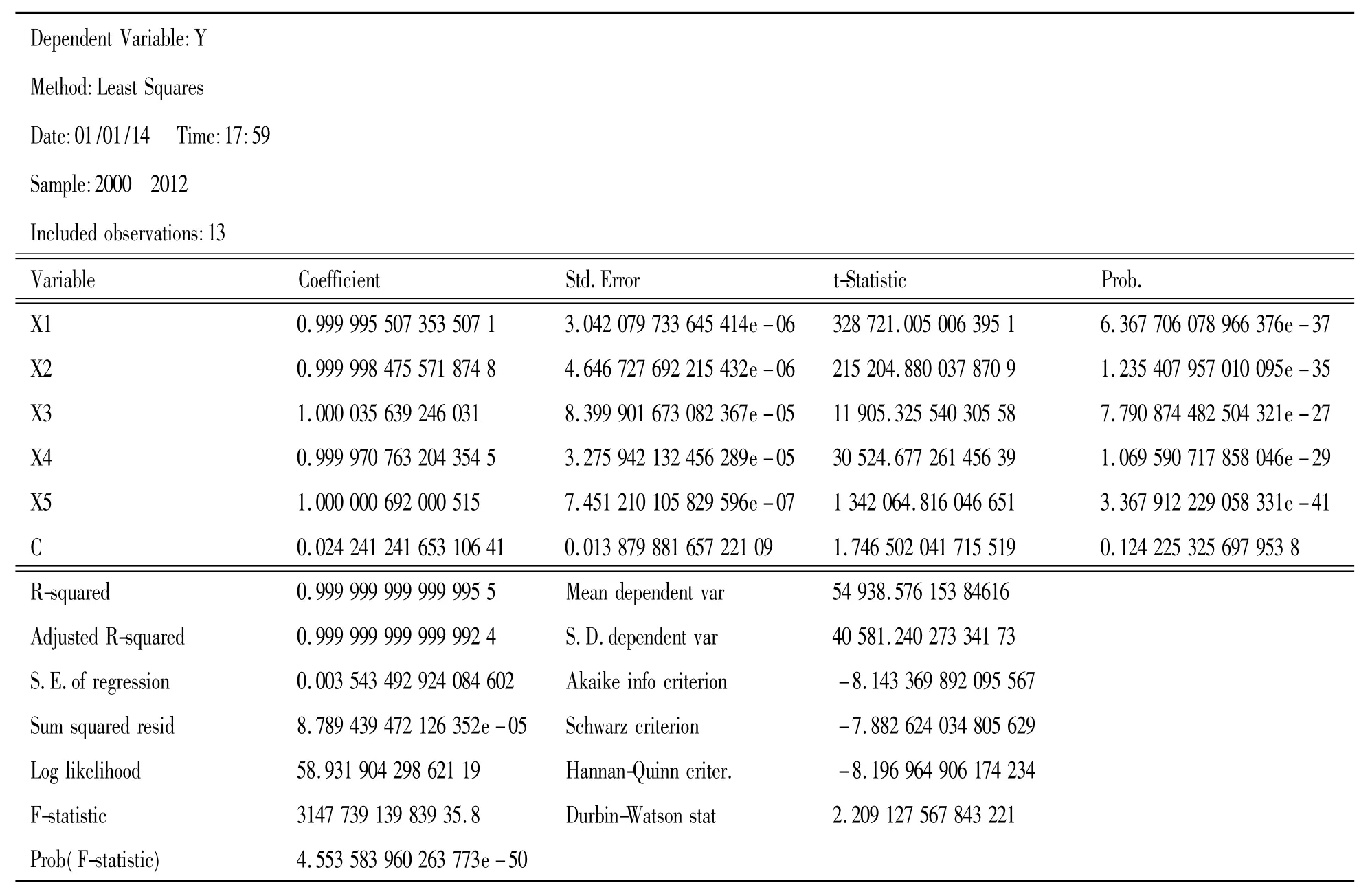
表2 “make equation”計算結果

(三)結果分析

根據表2的結果可知:

(1)建筑業總產值與參與建筑業的企業類型的多元線性回歸關系表達式為:

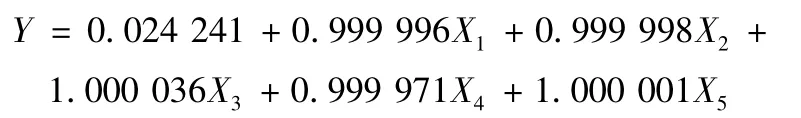
可知，建筑業總產值與參與建筑業的企業類型存在多元線性回歸關系。

(2)樣本回歸線對樣本觀測值的擬合程度結果:

可決系數R2≈1

調整的可決系數R2≈1

可知，該統計量接近1，擬合優度高。

(3)樣本回歸方程顯著性的F檢驗結果:

可知，模型的線性關系在95%和99%的置信水平下顯著成立。

四、結束語

從國有企業、集體企業、港澳臺商投資企業、外商投資企業、其他等5個方面對建筑業總產值進行多元線性回歸分析發現，建筑業總產值與參與建筑業的企業類型存在顯著的多元線性回歸關系。文章證明了這樣的關系存在，那么以后在統計建筑業總產值時，就可以重點從企業類型視角下的國有企業、集體企業、港澳臺商投資企業、外商投資企業、其他5個方面收集相關資料，減少工作量，提高工作效率。

［1］ 李子奈，潘文卿.計量經濟學［M］.3版.北京:高等教育出版社，2010.

［2］ 中華人民共和國國家統計局.中國統計年鑒［M］.北京:中國統計出版社，2013.

(責任編輯 周江川)