地形圖測量精度對土石方計算的影響分析

胡吉倫，程正逢，徐 輝

(中南電力設計院，湖北 武漢 430071)

地形圖測量精度對土石方計算的影響分析

胡吉倫，程正逢，徐 輝

(中南電力設計院，湖北 武漢 430071)

從滿足土石方工程量計算精度要求出發，分析現行不同行業測量規程在地形圖測量上的異同點，對全站儀三角高程測量的高差精度進行分析，提出地形點注記高程精度指標和地形點注記間距要求。同時對高程點高程精度對土石方計算的影響進行了分析。

高程點注記間距；測點高差精度；土石方工程量。

1 概述

在電力工程(變電站、發電廠)勘測設計過程中，如何為設計提供準確可靠的測量數據進行土石方工程量計算，是個多年來困擾測量人員的問題。隨著經濟的發展、工程成本的提高和工程預算制度的嚴格執行，設計計算土石方與實際土石方不合的矛盾日益突出。

現今常用的土方計算方法有方格法、斷面法、等高線法、數字地面模型法(DTM)、三角網法(TIN)，任何一種方法實際精度主要由原始數據的采集誤差和高程內插誤差兩方面決定。數據采集誤差來自測點設備誤差、測量誤差等，而高程內插誤差取決于測點密度和點位位置。

為進一步做好設計服務，滿足土石方計算誤差要求，使工程量計算更科學合理，需要對野外測點高程精度、測點的密度進行探討，找出科學合理的解決方案，滿足業主不斷提高的要求。

2 現行測量標準

目前廠區電力工程測量使用的測量規范是：《火力發電廠工程測量技術規程》(DL/T 5001－2004)行業標準，《水利水電工程測量規范》(SL 197－97)行業標準，《工程測量規范》(GB 50026－2007)國家標準，《1:500 1:1000 1:2000外業數字測圖技術規程》(GB/T 14912－2005)國家標準。在這些規范中，對于地形圖測繪精度，沒有提出要滿足施工土石方工程量計算的要求，但業主對計算土石方工程量有要求(如有的要求“土石方平衡工程量誤差不超過±5%”等)，這就對地形測量提出了挑戰。地形測量內容包括：地面地形地貌、地物信息和地下信息等。設計使用地形圖，一方面進行總平面布置，另一方面計算土石方工程量。而土石方工程量的計算，與地形圖高程點注記間距及精度、等高線或插求點有關。

2.1 高程點注記間距要求

對于高程點注記間距，各工程標準的要求見表1。

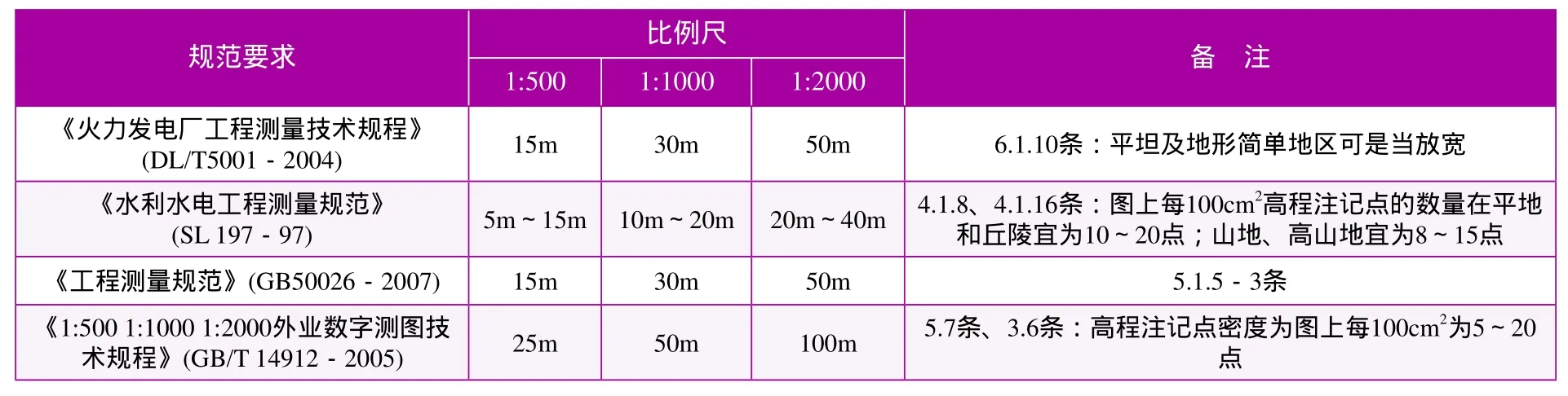
表1 幾種工程標準對測點密度要求

2.2 高程注記點精度要求

對于高程注記點的精度，各工程標準的要求見表2。

表2 幾種工程標準對高程注記點高程精度要求

2.3 等高線或插求點高程精度要求

對于等高線或插求點高程精度，各工程標準的要求見表3。

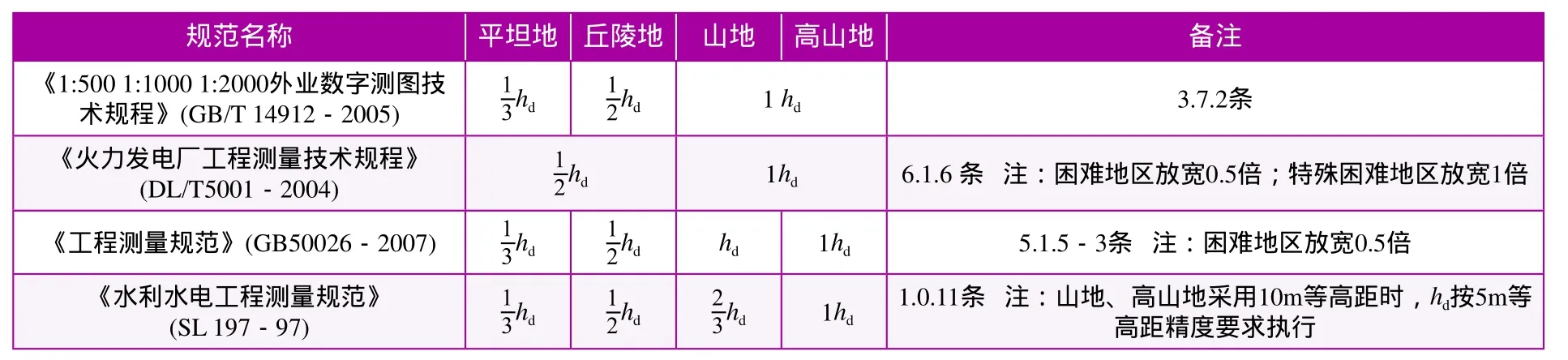
表3 幾種工程標準對等高線或插求點高程精度要求

2.4 幾種工程標準的比較

(1)測點密度方面，《工程測量規范》與《火力發電廠工程測量技術規程》注記點密度相同，《水利水電工程測量規范》注記點密度最高，《1:500 1:1000 1:2000外業數字測圖技術規程》注記點密度最低。

(2)高程注記點精度方面，《工程測量規范》與《火力發電廠工程測量技術規程》無規定，《水利水電工程測量規范》要求高程注記點精度高于《1:500 1:1000 1:2000外業數字測圖技術規程》。

(3)等高線或插求點高程精度方面，《水利水電工程測量規范》要求高于《火力發電廠工程測量技術規程》和《1:500 1:1000 1:2000外業數字測圖技術規程》，與《工程測量規范》要求相同。

3 全站儀采集高程點精度分析

從以上規范中可以看出，《水利水電工程測量規范》提出了高程注記點精度和較高的密度，比較好地規定出地形圖測圖精度。

由于土石方工程量與地形圖高程注記點精度和密度有關，而高程注記點精度與全站儀三角高程測量精度相關。下面對三角高程測量高差精度進行分析：

全站儀三角高程測量高差計算公式：

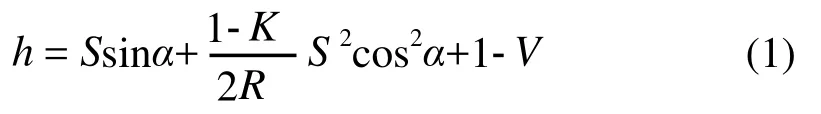
式中：h為高差；S為斜距；α為垂直角；I為儀器高；V為覘標高；K為大氣折光改正；R為地球半徑。

根據誤差傳播定律, 忽略微小項，得到高差中誤差為：

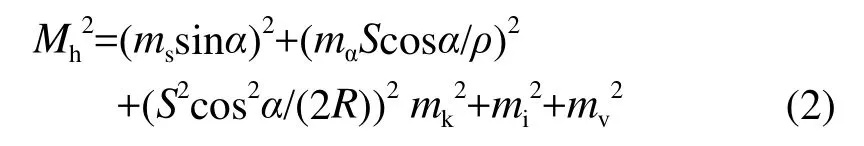
式(2)中，又因mk較小(一般為±0.03mm～0.05mm)，忽略，式(2)簡化為：

在全站儀地形圖測量中，取ms=±14mm(取自《工程測量規范》全站儀測圖要求，距離按700m計算)

mα=±18″(取自《工程測量規范》圖根電磁波測距三角高程的主要技術要求)

其他取值為：

按式(3)計算，垂直角和距離對高差的影響見表4。

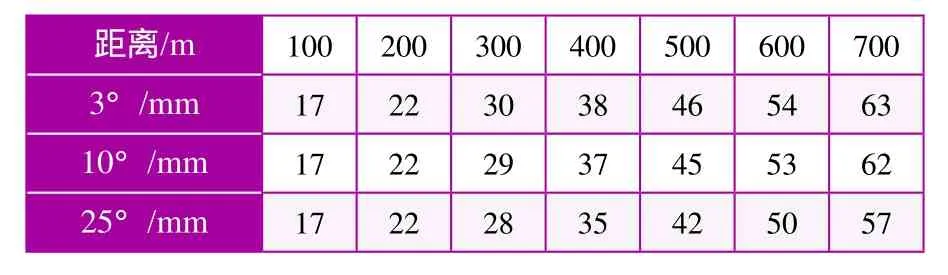
表4 垂直角和距離對地形點高差中誤差影響

根據《工程測量規范》，對于1:2000地形圖，全站儀測量地形點最大距離為700m，則平地、丘陵地形的地形點高差中誤差為63mm。圖根點高程中誤差不大于基本等高距的1/10，以基本等高距為1m計算，則有：

可以看出，測點高程誤差主要是測站點高程誤差。

取測點高差限差為±0.13m，測點高程限差為±0.3m。

從表4可知，垂直角對高差誤差的影響不明顯，距離影響明顯。在野外工作中，提高測站點高程精度將大大提高地形圖測點精度。

(1)除測點誤差外，在地形圖測量過程中，有些人為因素直接影響土石方工程量計算精度，如：測點點位不準，地形地物取舍不當等。因此，在野外測量過程中，測量人員需要注意如下事項：

①持鏡員應進行崗前培訓，地形圖測量立點時，棱鏡桿不應插入地下，應立于測點地面。

②地形地物的取舍應滿足規范要求，根據電力工程地形圖測量的特點，按照規范要求進行施測。

③測點應能反映地形的變化，如：坡度變化處、坎上坎下、溝底等，在測量稻田、旱地時，點位不應立在田、地中間的廂溝下面，應立在地臺上面，并能反映田、地的地面高度。

()總結不同規范的要求，結合工作實際，我們認為目前地形圖測量建議補充內容如下：

①地形點相對于測站點的高差限差為±0.15m；地形點高程限差為±0.3m。

②大比例尺地形圖測點密度見表5。

表5 地形點點位間距 (單位：m)

4 高程點精度對土方量計算的影響

4.1 采用不規則三角網計算土石方量的方法

不規則三角網(Triangulated Irregular Network，TIN)指將按地形特征采集的點按一定規則連接成覆蓋整個區域且互不重疊的連續三角形。TIN能較好地顧及地貌特征點、線，表示復雜的地形表面比矩形格網精確。我們將根據地形起伏變化的復雜性來確定采樣點的密度和采樣點的位置，從而可以避免地形平坦時的數據冗余，又能按地形特征點較好地逼近地形表面。在計算填方和挖方量的過程中，首先根據在挖前和挖后的地面特征點建立不規則三角網。在建立好的不規則三角網中，其每一個基本單元的核心是組成不規則三角形的三個頂點的三維坐標；從每個挖前三角形的三個頂點豎直向下引出三條直線，直到與挖后的地表面的三角網相交，便形成許多的三棱柱，這時整個區域的土石方地形便形成了由許多連續但不可微分的三棱柱組成的集合。分別計算出每個三棱柱的體積，所有的三棱柱體積之和便是整個區域的土石方量。

具體見圖1：

現假設，面ABC為挖前地表面TIN中的三角形，面DEF為挖后地表面上的三角形面，面A1B1C1為上下表面在水平面上的投影；點A、B、C為測區內挖前地表面的特征點，點D、E、F為測區內挖后地表面上的地形點，其三維坐標(X，Y，H)已知。

首先令：

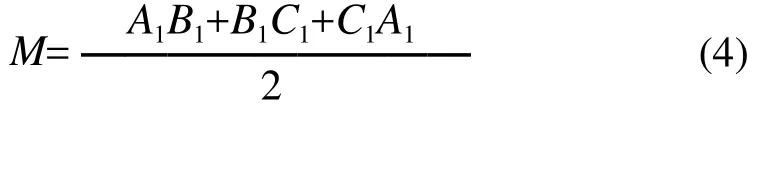
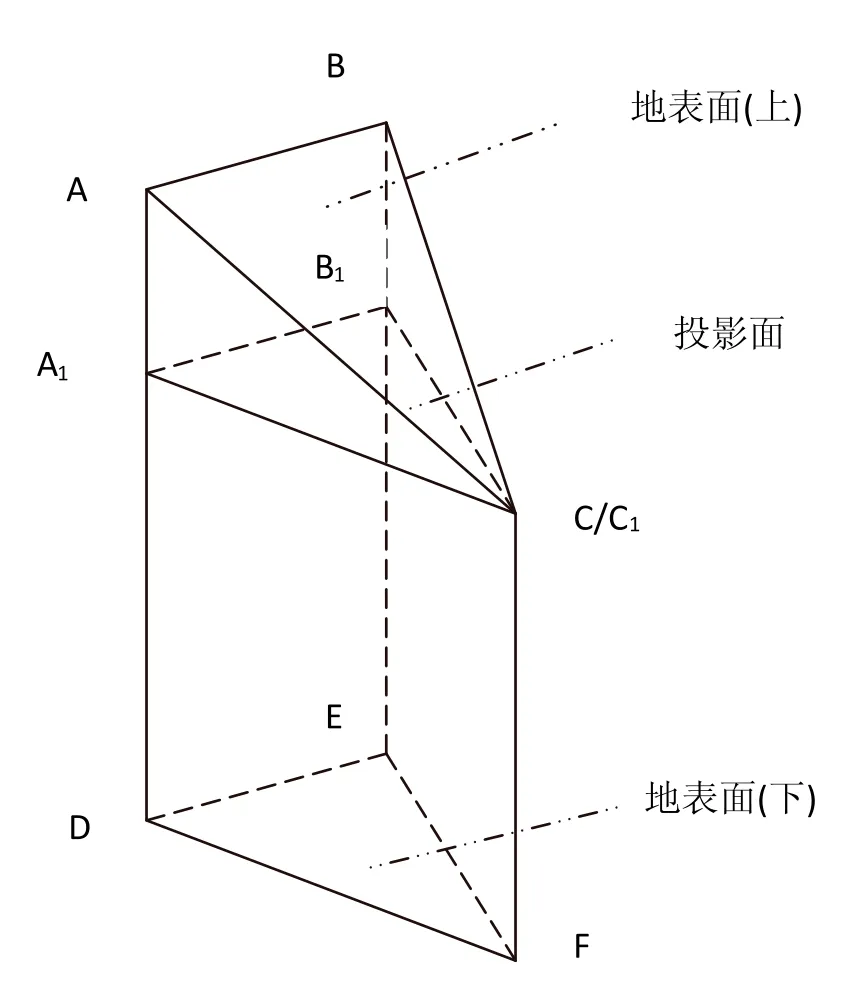
圖1 不規則三角網計算土石方量示意圖

則投影面的面積為：

其中A1B1、B1C1、C1A1、AD、BE、CF長度可由三角形幾何關系求得，圖1為三棱柱示意圖。這樣便求出了一個三棱柱的體積為V1；假設整個區域是由n個連續但不可微分的三棱柱組成，則整個區域的土石方量為：

式(7)中V1為各個不規則的三棱柱的體積。

4.2 高程點誤差對采用TIN計算土石方量的影響分析

由上面的計算公式可以看出，單個三棱柱的體積與上表面在水平面上的投影面積、三角形挖前挖后的頂點高差之和相關，計算區域內的TIN由離散高程點按德勞內法則組成，離散點的分布決定了三角形的分布，對于分布一定的TIN來說，決定其土石方計算精度的就是三角形頂點高差之和。僅考慮高程點測量誤差的影響，將每一個三角形面積看作一個常數，以挖方為例說明高程點高程誤差對土石方量計算的影響。

假設所有高程為同樣的方法測得，則高程點具有同樣的高程精度，假設其高程誤差為h。AD為A點高程減去挖方后的設計高程值，設計高程值為常量，則AD的誤差也為h，同理BE、CF的誤差也為h，將h值代入公式(6)，則：

則有

為了明確高程點的高程誤差對土方量計算誤差的影響程度，按以下方法進行了模擬計算：以一定面積的外業采集高程點作為理論數據，將高程點高程誤差分別按+0.1m、+0.2m、+0.3m進行假設，計算的挖方量及高程誤差影響比例見表6。

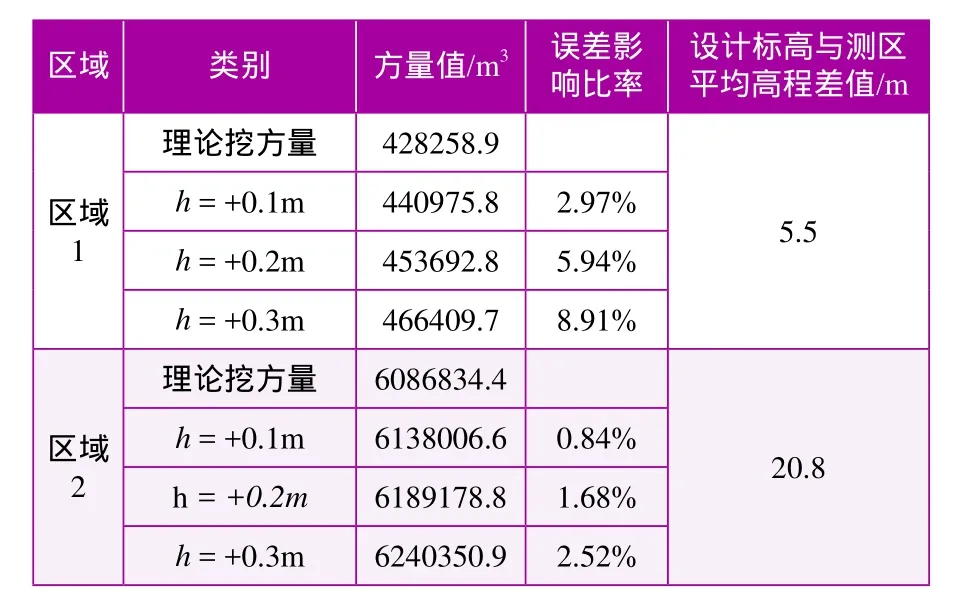
表6 高程誤差對挖方量的影響計算

由表6可以看出，高程點的高程誤差直接影響土方量計算的精度。

在實際的計算過程中，計算區域挖方體積只能依靠有限的三棱柱來模擬計算，為了盡可能提高區域體積計算的精度，有限的三棱柱的上表面三角形所代表的平面必須盡可能地接近地面實際情況，最大程度地模擬地面起伏變化，因此區域內構造TIN的高程點還要分布均勻，且具有足夠多的地形地貌特征點。

如何確定土石方開挖平均高差與測點精度關系，《水電水利工程施工測量規范》(DL/T 5173－2012)7.6.10規定“對同一區域土石方挖填工程量進行兩次獨立測量計算的土方量差值不超過7%或石方量差值不超過5%時，可取其平均值作為最后值。”，《水利水電工程施工測量規范》(SL 52－93)5.3.15規定“兩次獨立測量同一區域的開挖工程量其差值小于5%(巖石)和7%(土方)時，可取中數(或協商確定)作為最后值。”，結合表6，我們可以推算出挖方平均高差與測點精度關系。

我們假設計算挖方高差誤差與測點高程誤差相同。

設 M1為第一次測量工程量；M2為第二次測量工程量；S為挖方平均面積；ΔH為挖方平均高差；M為挖方平均工程量。

則工程量

2次工程量計算差值

由于每次測量均有誤差，對(1)、(2)式微分，按誤差傳播定律有

(18)式為挖方平均高差與高差精度的關系。

平均挖方高差與測量高差誤差關系見表7。站點的高差限差為0.15m，點的密度按表5要求執行。從我們使用測量儀器精度看，結合目前測繪工作現狀，對于地形點高差限差取0.15m，是可以滿足的。

表7 平均挖方高差與測量高差誤差關系 (單位：m)

從管理角度上看，在進行測量交樁過程中，需要使用測量儀器對現場關鍵地形點進行檢測，并將測量數據提交給監理和施工單位，以減少施工過程中施工單位提出土石方工程量不符合的矛盾。

隨著業主精細化管理的提高，對設計、施工管理日益細化，經濟指標量化，對土石方工程量計算會提出更高要求。這對我們測量人員是個新的挑戰，也為測量技術的發展提出了新的課題。

由于假設計算挖方高差誤差與測點高程誤差相同，表7可以作為野外地形圖測量高程注記點精度指標。

5 結論

根據以上分析，對于1:500或1:1000地形圖測量，在用于土石方工程量計算時，測點高程精度將直接影響其工程量計算，綜合考慮表7和工作實際，建議要求測點對于測

[1]GB 50026－2007，工程測量規范[S]．

[2]DL/T 5001－2004，火力發電廠工程測量技術規程[S]．

[3]SL 197－97，水利水電工程測量規范[S]．

[4]DL/T 5173－2012，水電水利工程施工測量規范[S]．

[5]楊成貴，羅奎，鄭瀟瀟．土石方工程的誤差分析[J]．天然氣與石油，2010，28(6)．

[6]李志林，朱慶．數字高程模型[M]．武漢：武漢大學出版社，2000．

[7]高井祥. 測量學[M]. 徐州：中國礦業大學出版社，2002.

Effect of Relief Map Measure Precision on Calculation of Earth Stone Square

HU Ji-lun, CHENG Zheng-feng, XYU Hui
(China Southern Electric Power Design Institute, Wuhan 430071, China)

In order to meet the design requirement on earthwork quantity calculation，this article analyses the similarities and differences on topographic map survey in the different surveying specifications, analysis the total station triangle elevation measurement accuracy and propose topographic point elevation accuracy index and topographic point note spacing requirements. At the same time, this article analyses the influence on earthwork calculation from point elevation accuracy.

spacing of the elevation ooint; elevation difference accuracy; earthwork quantity

P2

B

1671-9913(2014)03-0027-06

10.13500/j.cnki.11-4908/tk.2014.03.006

2013-05-27

胡吉倫(1957- )，男，湖北鄂州人，高級工程師，目前從事電力工程測量工作。