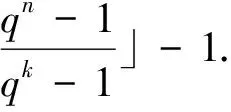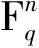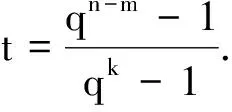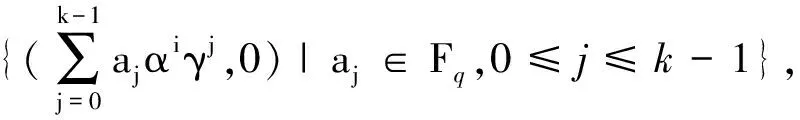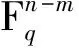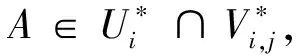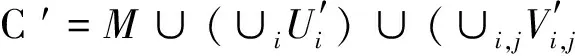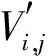最優常維碼界的一個注記

廖群英, 朱 娟

(1. 伊犁師范學院 數學與統計學院, 新疆 伊寧 835000; 2. 四川師范大學 數學與軟件科學學院, 四川 成都 610066)

1 引言及主要結果

設q為素數的方冪,Fq為q元有限域,W為Fq上的n維向量空間,P(W)為W的所有子空間的集合.對任意的A,B∈P(W),記

A+B={a+b|a∈A,b∈B},

同時包含A和B的最小子空間.近年來,R. Koetter等[1]在研究隨機網絡編碼時引進了算子信道的概念.他們同時也定義了常維碼,并說明了此類碼可以用來糾正或檢驗信息在算子信道傳輸中出現的錯誤.

子空間A與B之間的維數距離定義如下

d(A,B)=dim(A+B)-dim(A∩B)=

dim(A)+dim(B)-2dim(A∩B).

(1)

由此定義了空間P(W)上的一個度量[1].一個q元(n,M,D)或者(n,M,D)q碼C即為P(W)中一個M元子集,其最小維數距離D定義為

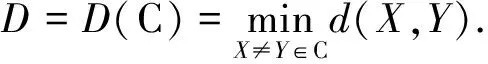
對任意正整數k≤n,記P(W,k)為W的全部k維子空間的集合.對任意m,0≤m≤n以及q≥2,

表示q元二項式系數,即高斯二項式系數[2].熟知,

一個q元(n,M,2δ,k)或(n,M,2δ,k)q常維碼定義為P(W,k)的一個M元子集,其最小維數距離為δ.由(1)式,維碼中任意2個碼字之間的維數距離必為偶數并且1≤δ≤k.一個(n,M,≥2δ,k)q常維碼即為P(W,k)的一個最小維數距離至少為2δ的M元子集.任意給定n,k,δ以及q,記Aq[n,2δ,k]表示參數為(n,M,≥2δ,k)q的常維碼所含碼字個數M的最大值.如果M=Aq[n,2δ,k],則稱常維碼(n,M,≥2δ,k)q為最優常維碼.常維碼的一個主要研究問題即是確定Aq[n,2δ,k],并且找出相應的最優常維碼.

不存在滿足漢明界的最優完全常維碼[3-4].在2003年,文獻[5]給出了線性認證碼的一個上界,等價于給出了常維碼的一個界.

命題1.1[5](Wang-Xing-Safavi-Naini界) 對任意最優常維碼Aq[n,2δ,k],

隨后,文獻[6]在2009年證明了Steiner結構即為達到Wang-Xing-Safavi-Naini界的最優常維碼,并且證明了常維碼達到Wang-Xing-Safavi-Naini界當且僅當其為某類Steiner結構.事實上,早在2002年,M. Schwartz等[3]構造了Steiner結構并證明了如下命題:

命題1.2對任意正整數k和l,

最近,T. Etzion等[7]將文獻[2,7-8]中的主要結果推廣到k不能整除n的情形.

命題1.3[7]設n≡r(modk),則對任意素數方冪q,均有

T. Etzion等[7]同時也將常維碼的概念推廣到C?P(W)的一般子集的情形,即:稱子集C是P(W)中的(n,M,d)碼,如果|C|=M并且對所有的U,V∈C,d(U,V)≥d,其中

d(U,V)=dimU+dimV-2dim(U∩V).

特別地,如果存在k,使碼C=(n,M,d)包含于P(W,k),則稱C為(n,M,d,k)碼.本文進一步討論最優常維碼的上界問題.通過改進文獻[7]中常維碼的構造方法,給出了某些特殊類型常維碼的界.進而證明了不存在同時達到Wang-Xing-Safavi- Naini界和最大距離可分界的最優常維碼.事實上,本文證明了如下主要結果:

定理1.4設n≡r(modk),0≤r≤k-1,則對任意素數方冪q,均有

以及

由命題1.1以及定理1.4,易得:

推論1.5對任意正整數n和k,

定理1.6對任意正整數n和k,

定理1.7不存在最優常維碼Aq[n,d≥2σ,k],同時達到Wang-Xing-Safavi-Naini界和最大距離可分界,即

2 主要結果的證明

為證明主要結果,需要如下引理.

引理2.1[7]設n≡r(modk),0

(I) 對?i∈{0,1,…,t-1}以及j∈{0,1,…,qm-2},令

M=〈(0,β0),(0,β1),…,(0,βk-1)〉=

(2)

Ui=〈(αi,0),(αiγ,0),…,(αiγk-1,0)〉=

以及

Vi,j=〈(αiγ0,βj),(αiγ1,βj),…,(αiγk-1,βj)〉=

易知

dimFqM=dimFqUi=dimFqVi,j=k,

0≤i≤t-1, 0≤j≤qm-2.

(5)

現在考慮常維碼

C=M∪(∪iUi)∪(∪i,jVi,j)=[n,δ,k]q(6)

的最小維數距離δ.

由(2)～(5)式以及α、β、γ的假設,易知

M∩Ui=M∩Vi,j={0},

0≤i≤t-1, 0≤j≤qm-2.

再由維數距離(1)式,dimFqM∩Ui=dimFqM∩Vi,j=0.于是由(5)式可得

d(M,Ui)=d(M,Vi,j)=2k-0=2k,

0≤i≤t-1, 0≤j≤qm-2.

(7)

Ui1∩Ui2={0}, 0≤i1≠i2≤t-1.

由(1)和(5)式

d(Ui1,Ui2)=2k-0=2k,

0≤i1≠i2≤t-1.

(8)

因此,對?i∈{0,1,…,t-1}以及j∈{0,1,…,qm-2},令A∈Ui∩Vi,j,則存在a0,a1,…,ak-1∈Fq以及b0,b1,…,bk-1∈Fq,使得

即

b0βj+b1βj+…+bk-1βj=0,

并且

a0αiγ0+…+ak-1αiγk-1=b0αiγ0+…+bk-1αiγk-1.

再由γ的假設易知:1、γ、…、γk-1是Fq-線性無關的,因此上式表明

b0+b1+…+bk-1=0,

并且

al=bl, 0≤l≤k-1,

即

于是

dimFq(Ui∩Vi,j)=k-1,

i=0,1,…,t-1,j=0,1,…,qm-2.

故由(1)和(5)式可得

d(Ui,Vi,j)=2k-2(k-1)=2,

i=0,1,…,t-1,j=0,1,…,qm-2.

(9)

現在來考察子空間Vi,j1∩Vi,j2,0≤i≤t-1,0≤j1≠j2≤qm-2.對?A∈Vi,j1∩Vi,j2,?al,bl∈Fq,0≤l≤k-1,使得

這表明

并且

由于α、αγ、…、αγk-1是Fq線性無關的,并且βj1≠βj2(ji≠j2).于是

從而

故

dimFq(Vi,j1∩Vi,j2)=k-1,

0≤i≤t-1, 0≤j1≠j2≤qm-2.

因此由(1)和(5)式可得

d(Vi,j1,Vi,j2)=2k-2(k-1)=2,

0≤i≤t-1, 0≤j1≠j2≤qm-2.

(10)

因此由(5)～(10)式以及常維碼的維數距離(1)式,可知δ=1并且

故

(II) 設M定義同(I).對?i=0,1,…,t-1以及j=0,1,…,qm-2,令

以及

因此

0≤i≤t-1, 0≤j≤qm-2.

現在考察Fq上的常維碼

類似于(I)中證明可得

0≤i,i1≠i2≤t-1,j=0,1,…,qm-2,

以及對?i1,i2∈{0,1,…,t-1},j1,j2∈{0,1,…,qm-2},其中,(i1-i2,j1-j2)≠(0,0),均有

于是由(1)式可知

(11)

即

并且

這表明

al=bl(0≤l≤t-1),

并且

注意到β為Fqm中的本原元素,故

a0=…=at-1=at+1=…=ak-1=0,

i≡j+t(modqm-1), 0≤t≤k-1.

從而存在i=0,1,…,t-1;j=0,1,…,qm-2,滿足

即

(12)

于是由(11)和(12)式,C*為Fq上的[n,2(k-1),k]q常維碼,并且

因此

這就完成了定理1.4的證明.

=〈(αi,0),(αi+1γ,0),…,(αi+k-1γk-1,0)〉=

以及

類似于定理1.4的(I)中的證明,可知C′是Fq上的常維碼[n,2k,k]q,并且

因此

由此給出文獻[7]中定理11,即本文中命題1.3的另一個證明.

定理1.6的證明對于k|n,由命題1.3可以得到

(13)

現在假設n≡r(modk)(0≤r≤k-1).注意到

如果q=k=2且r=1,則

且

(15)

故由命題1.1～1.3以及(13)～(15)式可知定理1.6成立.

定理1.7的證明否則,采用反證法.由命題1.1可知

即

因此

注意到d≤k,從而

這與q≥2的假設矛盾.

所以達到Wang-Xing-Safavi-Naini界的最優常維碼不存在,從而定理1.7成立.

致謝四川師范大學科研基金重點培育項目(13ZDL06)對本文給予了資助，謹致謝意.

[1] Koetter R, Kschischang F R. Coding for errors and erasures in random network coding[C]//Proc 2007 IEEE Int Sympos on Information Theory (ISIT’2007). Nice,2007:791-795.

[2] MacWilliams F J, SloaneN J A. The Theory of Error-Correcting Codes[M]. Amsterdam:North-Holland,1981.

[3] Schwartz M, Etzion T. Codes and anticodes in the Grassman graph[J]. J Combin Theory,2002,A97(1):27-42.

[4] Etzion T. Perfect byte-correcting codes[J]. IEEE Trans Inform Theory,1998,44:3140-3146.

[5] Wang H X, Xing C P, Safavi-Naini R. Linear authentication codes: bounds and constructions[J]. IEEE Trans Inform Theory,2003,49(4):866-872.

[6] Xiao S, Fu F W. Johnson type bounds on constant dimension codes[J]. Des Codes Cryptogr,2009,50:163-172.

[7] Etzion T, Vardy A. Error-correcting codes in projective space[J]. IEEE Trans Inform Theory,2011,57(2):1165-1173.

[8] Bu T. Partitions of a vector space[J]. Discrete Math,1980,31:79-83.

[9] Ho T, Koetter R, Médad M, et al. The benefits of coding over routing in a randomized setting[C]//Proceedings of the IEEE International Symposium on Information Theory. Yokohama,2003:442.

[10] Ho T, Koetter R, Médad M, et al. A random linear network coding approach to multicast[J]. IEEE Trans Inform Theory,2006,52:4413-4430.

[11] Tonchev V D. Codes and designs[C]//Pless V C, Huffman W C. Handbook of Coding Theory. Amsterdam:North-Holland,1998.