一種群體智能融合算法及其在應急設施選址的應用＊

許 駿，許曉東

（華中科技大學公共管理學院，湖北 武漢 430074)

一種群體智能融合算法及其在應急設施選址的應用＊

許 駿，許曉東

（華中科技大學公共管理學院，湖北 武漢 430074)

針對粒子群優化算法早熟及細菌覓食算法收斂慢的問題，提出了將量子粒子群優化與細菌覓食算法融合的一種群體智能融合算法。該算法將細菌覓食、量子計算理論及粒子群優化的優點進行融合，以細菌覓食算法為主體，將量子進化算法及粒子群優化算法嵌入其中，從而極大地提高了算法的性能。通過對三個標準函數求解和驗證，結果表明該算法提高了收斂精度及速度。最后用該算法求解公共衛生應急服務設施點選址問題，取得了較好的效果，說明了該算法的有效性。

群體智能算法；量子粒子群優化；細菌覓食算法；應急選址

1 引言

群體智能算法［1，2］是一門新興的優化計算方法，自20世紀80年代出現以來，引起了多個學科領域研究人員的關注，已經成為優化技術領域的一個研究熱點。這類算法的主要應用對象是優化問題中的難解問題，也就是優化理論中的NP-hard問題。

群體智能算法本質上是一種概率搜索，不需要問題的梯度信息，并具有如下特點：（1)群體中的個體代表問題空間中的一個解，能感知周圍的局部信息且遵循的規則非常簡單，群體智能易于實現；（2)個體在解的空間是分布式的，不存在直接的中心控制，這樣即使有個別個體出現故障，也不會影響群體對問題的求解，具有較強的魯棒性。同時，個體之間可以相互作用從而表現出群體的高度智能。群體智能算法的出現，使得原來一些復雜而且難以用常規優化算法進行處理的問題得到了解決，在工程實際中得到了廣泛應用。常用的群體智能算法有遺傳算法、粒子群算法、細菌覓食算法、蟻群算法等。

群體智能算法的理論研究主要是研究算法特性，改進其不足，提高其性能，主要包括兩個方面：一是從群體智能算法的自身特性加以研究，改進其性能；二是將群體智能算法之間或者與其它算法融合，產生性能更佳的融合智能算法。本文提出了將量子粒子群優化與細菌覓食融合的算法，該算法結合了粒子群優化和細菌覓食算法的特點，并利用有關量子計算的理論基礎使之適用于離散空間。然后，通過標準函數進行驗證，進而應用于求解應急服務設施點選址問題。

2 量子粒子群與細菌覓食的融合算法

2.1 量子粒子群與細菌覓食的融合策略

粒子群優化PSO（Particle Swarm Optimization)算法首先由 Kennedy J和 Eberhart R C［3］提出，由于其簡潔性和快速性，一經提出便引起許多研究者的關注，主要歸結為算法本身改進［4，5］、算法拓撲結構改進［6，7］、算法參數的改進［8］、混合粒子群算法［9］等方面的研究和改進。這些研究使PSO成為一種有競爭力的群體智能優化技術，并廣泛應用于連續空間的尋優問題。

其中，k為迭代次數，ω為權系數，c1、c2為加速因子，r1、r2為［0，1］的隨機數。

在式（1)所描述的粒子速度進化方程中，第一項是粒子先前的速度，第二項代表“認知”部分，但僅考慮了粒子自身的“經驗”，第三項則代表了“社會”部分，即粒子間的社會信息共享。這樣粒子在相互作用下，有能力到達新的搜索空間。不過，雖然它的收斂速度較快，但對于復雜問題，容易陷入局部最優點［10］。

細菌覓食算法BFA（Bacterial Foraging Algorithm)是由Passino K M［11］于2002年提出來的一種仿生隨機搜索算法，通過模擬人類腸道中大腸桿菌的覓食行為，在搜索過程中通過營養分布函數來判斷搜索算法的優劣。該算法因具有群體智能算法并行搜索、易跳出局部極值等優點，成為生物啟發式計算研究領域的又一熱點。

在BFA中，優化問題的解對應于搜索空間中的細菌的狀態，即優化函數的適應度值。BFA包括趨化、復制和驅散三個步驟［12］，其主要步驟為趨化行為。細菌的趨化性操作可表示如下：

其中，θi（j，k，l)表示細菌i在第j次趨化操作、第k次復制操作和第l次驅散操作時的位置，c（i)表示趨化步長，φ（j)表示旋轉后選擇的一個隨機前進方向。

由于BFA在趨化中采用任意方向進行翻轉，沒有利用歷史信息，導致收斂速度較慢。2008年Dasgupta S和 Das S等人［13，14］對趨化操作分析后指出：當適應度函數形狀較為平坦時，趨化在接近優化值時會產生振蕩，文獻［13，14］建議對趨化步長給以約束。本文利用PSO中個體極值和全局極值信息來確定細菌前進的方向，從而確定趨化的最佳方向，表達為：其中r1i、r2i分別為粒子歷史最優和全局最優權系數，通過與當前粒子適應度值比較而確定其值，表達為：

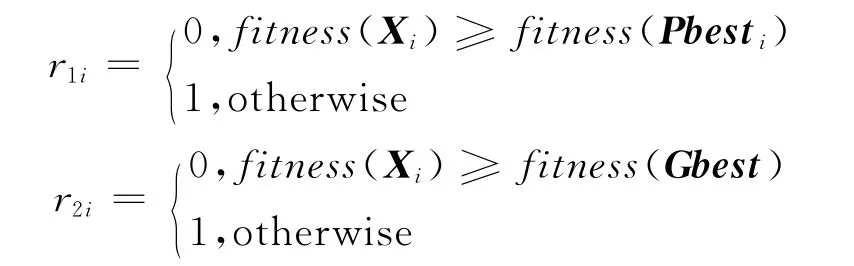
趨化步長對收斂性能影響較大，步長越大算法收斂越快，但易跳過最優值，而較小步長則增加了搜索時間。本文根據迭代次數自適應地改變步長，即開始使用大的步長，接近最優值時采用小步長，即：

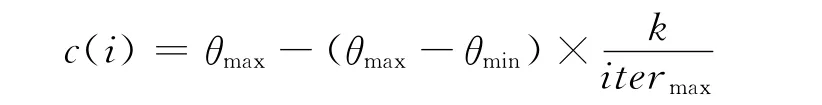
其中，itermax是最大迭代次數，k是當前迭代次數。改進后趨化操作的進化方程為：

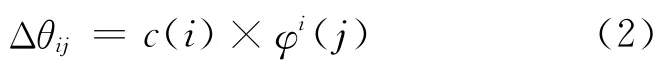
但是，上述對算法的改進策略僅適用于連續解空間。為了適應于離散空間，本文利用量子計算理論基礎，采用量子比特方式來表示每個細菌位置的狀態。一個具有n個量子比特位的系統可以描述為［15］：

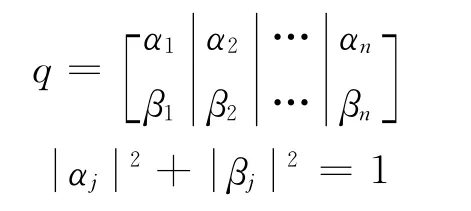
量子比特位的狀態改變可由進化方程（2)通過量子旋轉門計算得到［15］，即狀態更新方程為：

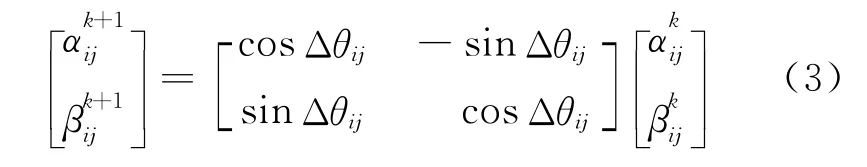
假設第i個細菌的位置向量Xi＝ ｛xi1，…，xin｝，位置向量的更新由其存儲在量子比特q中的β值確定，即：

2.2 量子粒子群優化與細菌覓食融合算法的實現

細菌位置代表一個解，解的優劣由系統適應度函數來確定。融合算法搜索最優解的步驟如下：

Step 1 初始化參數設置。其中，n為搜索空間維數；S為細菌種群數；Nc為趨化循環次數；Nre為復制循環次數；Ned為遷移循環次數；Ped為遷移概率；θmin、θmax為最小、最大旋轉角；、為1/。

Step 2遷移循環：l＝l＋1。

Step 3復制循環：k＝k＋1。

Step 4趨化循環：j＝j＋1。

Step 4.1選取細菌i，計算細菌i所在位置的適應度值：J（i，j，k，l)，并保存該值到Jlast；

Step 4.2由公式（2)計算細菌i每一位的旋轉值；

Step 4.3由公式（3)和公式（4)計算細菌i的新位置，并計算新位置的適應度值J（i，j，k，l)；

Step 4.4更新細菌i的局部最優值和種群全局最優值。

Step 5循環Step 4，直到趨化循環完畢。

Step 6復制：將適應度值差的細菌淘汰一半。為保證個體總數一致性，再對剩余的細菌進行復制。

Step 7重復Step 3，直至復制循環完畢。

Step 8遷移：以一定的概率Ped選取部分細菌，將其驅散到其它位置，剩余細菌的位置保持不變。

Step 9重復Step 2，直至遷移循環完畢。

Step 10結束。

2.3 算法性能測試

目前常用求解測試函數的最優值的問題來檢驗智能優化算法，這些測試函數有單峰，也有多峰的，函數解的分布是連續變化的。本文使用下列三個標準函數來驗證群體融合智能算法的精度及收斂性能。

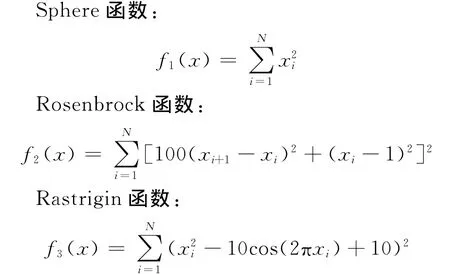
上述三個標準函數的維數為N。其中，Sphere函數具有單峰，最小值f（0)＝0，該函數的特點是曲面平滑，梯度信息總是能指向全局最優；Rosenbrock函數也是一個單峰函數，曲面光滑，但梯度信息經常誤導算法的搜索方向，算法較難搜索到全局最優解，全局最小值f（1)＝1；而Rastrigin函數具有多峰，有許多局部最小值，很難找到全局最優解，優化算法易陷入局部最優點，全局最小值f（0)＝0。

（1)算法參數分析。

本文提出算法中沒有太多需要調節的參數，因此只對最大、最小旋轉角、種群規模等參數進行分析。趨化操作及復制操作影響可參考文獻［13］，最大迭代次數分析由下文給出。

種群規模表示算法中同時進行搜索的細菌數目，決定了目標函數達到收斂值需要進行評價的最少次數。一般而言，種群規模大有利于在狀態空間內更充分搜索，同時可減少迭代次數，但是評價次數也相應增加。圖1是使用Rastrigin函數在不同種群規模下迭代1 000次時，計算機所用的時間及收斂值。從圖1中可以看出，種群規模選擇在20～40可取得較為合理的結果。

最大、最小旋轉角選用文獻［15］推薦值0.05π和0.001π，圖2顯示的是種群分別為10和30的情況下迭代1 000次不同最大、最小旋轉角的組合對收斂性能影響的結果。從圖2中可知，最大、最小旋轉角分別選用0.05π和0.01π最佳。

（2)算法性能分析。

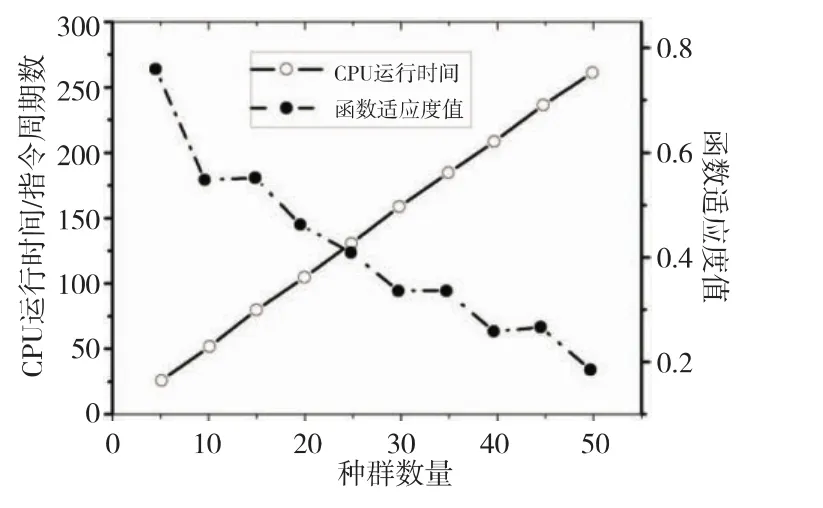
Figure 1 Influence of population size on the performance of algorithm圖1 種群數量對算法性能的影響

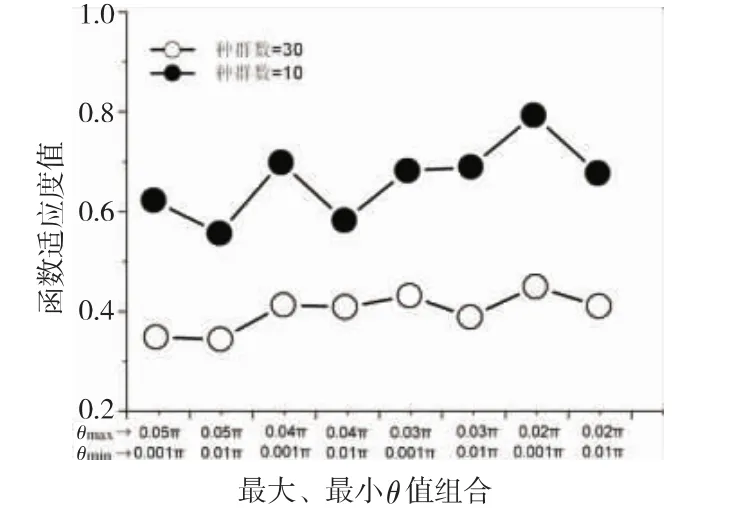
Figure 2 Influence of maximum ＆minimum rotation angle combination on the performance of algorithm圖2 最大、最小旋轉角組合對算法性能的影響

為了驗證本文提出的群體智能融合算法的收斂精度及收斂時間，本文采用前述三個經典標準函數進行驗證，并同時與其它算法進行比較。使用的參數為：遷移概率Ped＝0.25，最大、最小旋轉角分別取0.05π和0.01π，細菌種群數S＝20、復制次數Nre＝4、遷移次數Ned＝5，趨化次數Nc則隨函數復雜程度不同而變化。

首先，用 GA-BFO［16］、PSO-BFO［17］及本文算法分別對標準函數求解，每個函數獨立執行50次，計算均值及方差，收斂精度結果見表1，收斂速度結果見表2。

表1列出了不同算法對標準函數收斂到0.001或運行到規定的最大迭代次數時的情況（表中的黑體標記為不同算法收斂的最好值，方差為0的沒有標明)。從表1中可以看出，對于Sphere函數，維數為15時表中所選算法都能很快地收斂。總體來說，本文提出的融合算法收斂精度較其他算法高，特別當函數的維數比較大時。表2展示了函數收斂到規定閾值0.000 1時，算法獨立運行50次的迭代次數的均值與方差。從表2可以看出，對于Sphere函數，所有算法都能收斂，但對于Rosenbrock、Rastrigin兩個函數，在高維時，只有本文提出的算法能夠收斂，其它算法由于早熟而不能收斂到規定值（算法迭代的最高次數不高于1010)。

3 本文提出的算法求解公共衛生應急服務設施點選址問題

3.1 建模

直接面對居民“最后一公里”的應急服務設施點的選址對保障應急資源在短時間內高效地提供給受威脅地區每個居民是至關重要的，其選擇影響到衛生應急中應急資源供應最大最優，影響著整個系統的快速反應能力。對于分布寬廣的“最后一公里”的應急服務設施點的選址，必須確保覆蓋到所有災區中每一戶家庭，同時，為防止意外，每個行政區內至少要設置兩個應急服務設施點。顯然，設施點的數量與其容量及服務的人數有關，每個設施點需要的資源需要統籌規劃，以確保在規定時間內完成任務。本文中假設每個設施點的資源已確定，即容量已知，服務對象到相應設施點的距離不超過設置的最遠距離，在上述條件下確定應急服務設施點的數量。

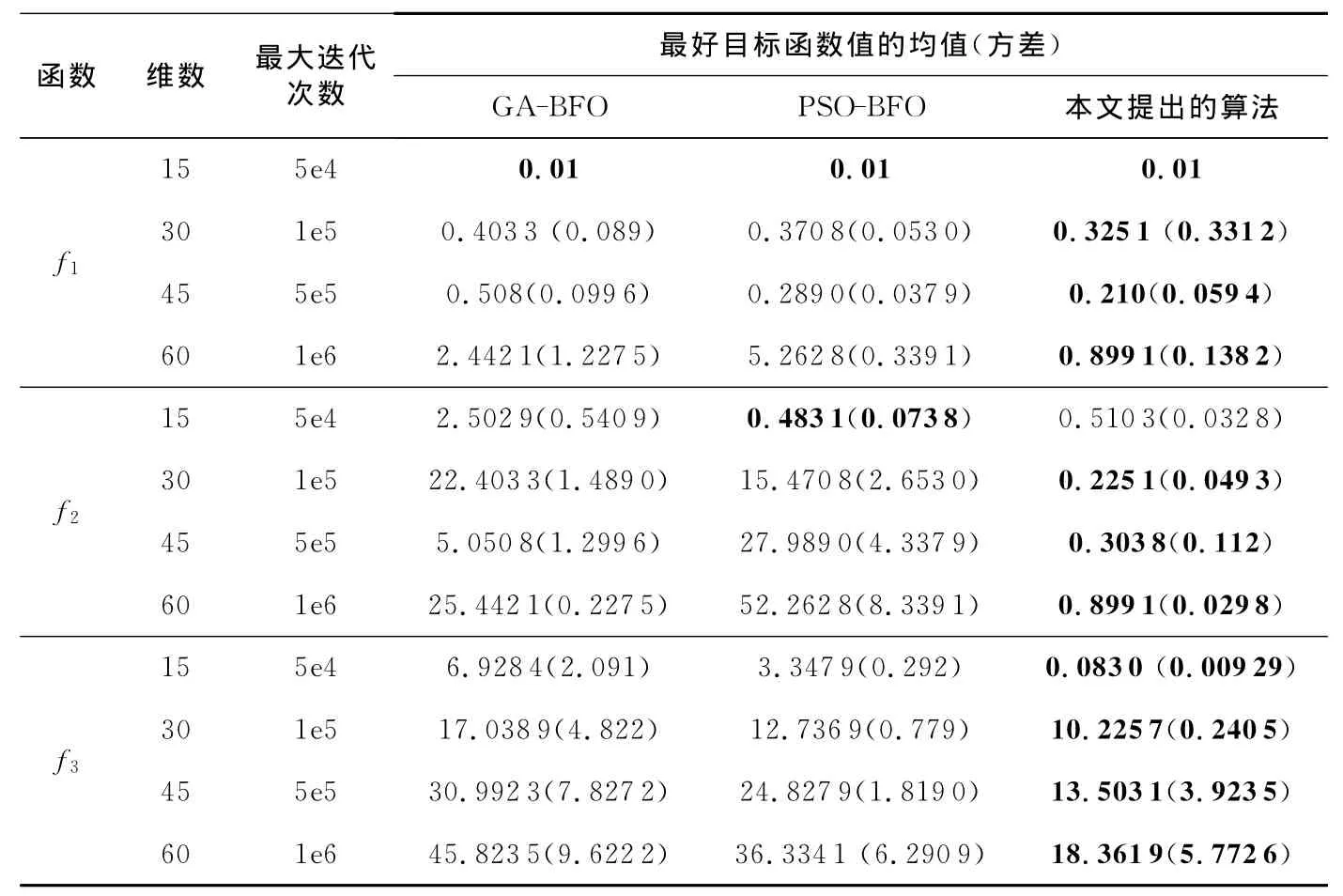
Table 1 Mean and variance of the objective function after different algorithm running independently（N＝50)表1 不同算法獨立運行后目標函數的均值及方差（N＝50次)

Table 2 Comparison of iteration number to the convergence of different algorithm running to the provisions threshold（N＝50)表2 收斂到規定閾值0.000 1時不同算法運行的迭代次數比較（N＝50次)

選址問題本身是一個非常經典的問題，有成熟的解決模型，然而應急服務設施點選址問題與傳統選址問題具有不同的優化約束與目標，前者時效性可能非常重要，而后者則更加關注成本。選址問題已被證明是一類極難優化的問題集，即NP-hard問題，至今未能有效精確求解［18］。已有的精確式算法都是指數級的，無法解決現實問題（中、大規模)。在實際應用時，近似算法特別是智能優化算法是求解NP-hard問題的有效方法之一［19］。本文通過對公共衛生應急服務設施點選址進行了建模，并用本文提出的算法求解應急服務設施點選址問題。

為了確定應急服務設施點的數量及服務的范圍，本文首先對要服務的目標區域離散化，即將目標區域劃分成大小為一平方公里的網格。每個網格與所服務的人口聯系起來，可認為是一個候選的應急服務設施點。對給定的目標區域，可以使用如下參數來描述與設施點有關的變量：

kem：事件發生地行政區的數目；

Gi：在行政區i內所有網格的集合，i≤kem；

cl：網格l內的應急服務設施點容量；

pr：網格r內的人口數量；

d（r，l)：網格r、l之間的距離；

dmax：服務對象到相應的應急服務設施點允許的最遠距離。

決策變量設為：

yl：如果網格l內設置了應急服務設施點，則為1，否則為0；

xrl：如果網格l內的應急點為網格r內的公民服務，則為1，否則為0。

則應急服務設施點的選址可用如下數學模型來描述：

目標函數在滿足需求的條件下，使應急服務設施點的數目最小。其中，約束條件（5)保證在每個行政區內至少要設置兩個應急服務設施點，以防在意外災難發生而必須關閉設施點時，另一個應急設施點還能正常運行；約束條件（6)限制了每個用戶到達應急服務設施點的距離需小于最遠行駛距離；約束條件（7)保證每戶都能得到服務；約束條件（8)則要求設施點所能提供的服務量不能大于其容量；約束條件（9)限定決策變量是0/1變量。約束條件

3.2 實現

為了求解公共衛生應急資源選址問題，必須先確定問題空間的編碼方式、粒子適應度函數、種群的初始化等。

（1)問題的編碼方式。

當采用本文提出的算法求解問題時，首先必須在目標問題實際表示與種群個體之間建立聯系，即采用某種編碼方式將解空間映射到編碼空間。本文將應急區域用網格進行劃分，對網格進行編號，然后采用二進制編碼，碼的位數與網格的編號一一對應。比如，現有編號為0、1、2、3、4、5的網格，則對應的二進制編碼為110010，位0對應于0號網格，位1對應于1號網格，依次類推。二進制相應位如果是“0”表示在此網格中沒有應急服務設施點，是“1”則表示網格中設置有應急服務設施點，上述例子中，1、4、5號網格中應設置設施點。網格排列的值的變化構成了問題的狀態空間，顯然，一個排列代表了一個解。

（2)確定適應度函數。

適應度函數是由問題的目標函數變化而成的。對應急服務設施點選址問題，還必須滿足約束條件。為此，適應度函數包括三部分：第一部分與目標函數有關，本文應急服務設施點采用了二進制編碼方式，因此，解的二進制中“1”的個數即為設施點的數量，此部分設為fem1；對于不滿足約束條件（5)的行政區的數量設為fem2，這一部分必須加入到適應度函數中，為第二部分；第三部分與服務對象有關，涉及到約束條件（6)～約束條件（8)。依據最近法則，確定可為每個服務對象提供服務的設施點，當超過其容量時，到次近的設施點，直到無設施點可用或者到設施點的距離超過設定的最遠距離為止。此時對剩余的服務對象進行聚類統計，相互之間的距離小于最遠距離的歸為一類，分類的數量即為fem3，則適應度函數f＝fem1＋fem2＋fem3，在fem2、fem3都為零的情況下適應度函數越小越優。

（3)種群的初始化。

種群個體數量一般在20～40，與解空間的狀態有關，本文數量選為30。個體的初始位置采用貪婪算法選取，使之滿足所有約束條件。

3.3 算例

以武漢市為例，總人口978萬人，有13個行政區，用一平方公里網格對區域作劃分，每個行政區網格數量在34～2 261，每個網格人口數量在321～20 711。模型的問題規模約束條件和0/1變量數量從最小1 225＊1 190到最大5 116 644＊5 114 382。

為了說明本算法性能，本文分別用LINGO 10、GA-BFO和本文算法求解，迭代次數1 000次，計算結果如表3所示。

Table 3 Calculating results of running time and facilities point number of different algorithm表3 不同算法的運行時間及設施點數量計算結果

從表3中可以看出，當應急設施點容量為2 000人/h時，采用LINGO 10的運算時間最短，但當問題的規模變大，如設施點容量為500人/h時，則不能求解，而本文提出的算法僅用90分鐘就可以完成。因此，求解問題規模越大，本文提出的算法優勢越明顯。

表4的結果顯示了當應急服務設施點容量不同時，限制的最遠距離與應急服務設施點數量之間的關系。圖3則顯示在設施點容量和最遠距離一定時，實際旅行距離下到應急設施點接受服務的居民數量分布的概率。

Table 4 Numbers of facility points needed in different capacity under different maximum distances表4 不同容量下不同最遠距離所需設施點的數目

Figure 3 Relationship between the actual driving distance and the residents distribution proportion（parametric assumption：capacity＝1 500person/hour，maximum distance＝10km)圖3 實際行駛距離與居民分布比例的關系

4 結束語

本文基于細菌覓食算法、粒子群優化及量子計算的特點提出的群體智能融合算法，是將粒子群優化的思想融入細菌覓食算法中，充分利用了個體的信息，使收斂速度大大加快，解決了由于隨機的搜索方向導致細菌覓食算法收斂時間增加的問題，從而極大地提高了算法的性能。同時，采用量子比特位來存儲細菌的狀態，從而使算法適用于離散空間。本文通過對三個標準函數在不同維數下的求解，驗證該算法在收斂性能方面的提高。最后用該算法求解公共衛生應急選址的問題，得到了較好的效果，表明該算法是一種有效的方法。

［1］ Bonabeau E，Dorigo M，Theraulaz G.Swarm intelligence：From natural to artificial systems［M］.1st edition.New York：Oxford University Press，1999.

［2］ Bonabeau E，Dorigo M，Theraulaz G.Inspiration for optimization from social insect behaviour［J］.Nature，2002，406（6)：39-42.

［3］ Kennedy J，Eberhart R C.Particle swarm optimization［C］∥Proc of IEEE International Conference on Neural Networks，1995：1942-1948.

［4］ Clerc M，Kennedy J.The particle swarm-explosion，stability，and convergence in a multidimensional complex space［J］.IEEE Transactions on Evolutionary Computation，2002，6（1)：58-73.

［5］ Ratnaweera A，Halgamuge S，Watson H.Self-organizing hierarchical particle swarm optimizer with time-varying accelerating coefficients［J］.IEEE Transactions on Evolutionary Computation，2004，8（3)：240-255.

［6］ Hu X H，Eberhart R C.Multi-objective optimization using dynamic neighborhood particle swarm optimization［C］∥Proc of the Congress on Evolutionary Computation，2002：606-607.

［7］ Mendes R，Kennedy J，Neves J.The fully informed particle swarm：Simpler，maybe better［J］.IEEE Transactions on Evolutionary Computation，2004，8（3)：204-210.

［8］ Eberhart R C，Yu S.Guest editorial special issue on particle swarm optimization［J］.IEEE Transactions on Evolutionary Computation，2004，8（3)：201-203.

［9］ Higashi N，Iba H.Particle swarm optimization with Gaussian mutation［C］∥ Proc of the Congress on Evolutionary Computation，2003：72-79.

［10］ Kennedy J，Mendes R.Neighborhood topologies in fully-informed and best-of-neighborhood particle swarms［J］.IEEE Transactions on Systems，Man，and Cybernetics，2006，36（4)：515-519.

［11］ Passino K M.Biomimicry of bacterial foraging for distributed optimization and control［J］.IEEE Control Systems Magazine，2002，22（3)：52-67.

［12］ Das S，Biswas A，Dasgupta S.Bacterial foraging optimization algorithm：Theoretical foundations，analysis，and applications［M］.Heidelberg：Springer-Verlag，2009：23-55.

［13］ Dasgupta S，Das S，Abraham A，et al.Adaptive computational chemotaxis in bacterial foraging algorithm［C］∥Proc of the 2nd International Conference on Complex，Intelligent and Software Intensive Systems，2008：64-71.

［14］ Das S，Dasgupta S，Biswas A，et al.On stability of the chemotactic dynamics in bacterial foraging［C］∥ Proc of International Conference on Soft Computing as Transdisciplinary Science and Technology，2008：245-251.

［15］ Han K H，Kim J H.Quantum-inspired evolutionary algorithm for a class of combinatorial optimization［J］.IEEE Transactions on Evolutionary Computation，2002，6（6)：580-593.

［16］ Kim D H，Abraham A，Cho J H.A hybrid genetic algorithm and bacterial foraging approach for global optimization［J］.Information Sciences，2007，177（18)：3918-3937.

［17］ Biswas A，Dasgupta S，Das S，et al.Synergy of PSO and bacterial foraging optimization：A comparative study on numerical benchmarks［M］∥Innovations in Hybrid Intelligent Systems，2007：255-263.

［18］ Yang Feng-mei，Hua Guo-wei，Deng Meng，et al.Some advances of the researches on location problems［J］.Operations Research and Management Science，2005，14（6)：1-7.（in Chinese)

［19］ Edson L F S，Luiz A N L，Marcos A P.A decomposition heuristic for the maximal covering location problem［J］.Advances in Operations Research，2010，2010：1-12.

附中文參考文獻：

［18］ 楊豐梅，華國偉，鄧猛，等.選址問題研究的若干進展［J］.運籌與管理，2005，14（6)：1-7.

A fusion algorithm of swarm intelligence and its application in emergency services facility location

XU Jun，XU Xiao-dong
（School of Public Administration，Huazhong University of Science and Technology，Wuhan 430074，China)

In order to solve the problem of prematurity of swarm intelligence algorithm and slow speed of convergence of bacterial forging algorithm，an algorithm is proposed，which fuses quantum particle swarm together with bacteria foraging optimization.After considering the advantages of bacteria foraging optimization，quantum computing theory and particle swarm optimization，the proposed fusion algorithm takes the bacterial foraging algorithm as the main body and embedded quantum evolutionary algorithm and particle swarm optimization algorithm into it，thus improving the performance of the algorithm greatly.Through solving and validating the three criteria functions，the results show that the proposed fusion algorithm improves convergence precision and speed.Finally，the proposed algorithm is used to solve public health emergency service facility location problem and achieves good results，proving its effectiveness.

swarm intelligence algorithm；quantum particle swarm optimization；bacterial foraging algorithm；emergency service facilities point location

TP399；X43

A

10.3969/j.issn.1007-130X.2014.04.017

2012-10-08；

2013-03-05

通訊地址：430015湖北省武漢市江岸區江漢北路24號

Address：24Jianghan Rd North，Jiang’an District，Wuhan 430015，Hubei，P.R.China

1007-130X（2014)04-0667-07

許駿（1971-)，女，湖北隨州人，博士生，研究方向為公共安全預警與應急管理。E-mail：xujun＠whcdc.org

XU Jun，born in 1971，PhD candidate，her research interests include public safety early warning，and emergency management.