基于SiCp/6061Al復合材料二維真實微觀結構的簡化模型

中北大學機電工程學院 李超 原梅妮 李立州 郎賢忠

前言

顆粒增強金屬基復合材料（MMC）由于具有高的比強度、比剛度及良好的耐磨性、熱穩定性等優點，目前已經成功被應用于航空航天、汽車及體育器材等領域[1]。金屬基復合材料的力學性能及損傷破壞規律取決于復合材料的微觀結構特征，而復合材料的真實微觀結構往往具有的結構復雜、計算量大等特點，致使研究人員多采用簡化模型以及單胞模型的方法進行有限元仿真和計算。雖然這些方法在很大程度上降低了計算量，有利于顆粒增強金屬基復合材料力學特性的規律總結與開發利用，但不同模型中由于增強顆粒的不同形狀、局部密度、體積分數等因素，均會對金屬基體的流動性、顆粒的約束能力、顆粒與基體的接觸面積以及顆粒的轉動造成不同程度的影響，使得計算結果和真實情況產生一定的偏差[2]。

本文以SiCp/Al復合材料的微觀電鏡圖為基礎，建立了含有顆粒真實形狀的微觀模型。以此模型為基礎，建立了含有相同顆粒體積分數、體積與坐標的多種簡化模型。使用了子模型技術對不同模型進行有限元建模和計算，通過對比不同模擬的計算結果與云圖，驗證不同模型的有效性。

1 模型建立

1.1 材料參數

在復合材料的有限元模型中，S i C顆粒為線彈性，其彈性模量Ep=440 GPa，泊松比νp=0.17。6061鋁為具有各向同性的彈塑體，其彈性模量為EAl=70 GPa，泊松比νAl=0.33[3]。基體的彈塑性應力—應變關系滿足Ludwik硬化法則[4]：

其中，σY和εp分別表示流變應力和塑性應變，表示屈服應力，h和n分別表示硬化系數與硬化指數。與6061鋁相對應的參數為[5]：

1.2 CAD模型

本文使用的SiC p/6061 Al復合材料，其顆粒體積分數為15%。以復合材料的S E M圖為基礎，通過設置適當的閾值等參數，對S E M圖像中的像素進行逐一識別，生成如圖1所示的C A D模型，在此定義為原始模型。

圖1 CAD模型（原始模型）的建立過程

1.3 多種簡化模型的建立

本文使用的簡化模型包括三種：圓形顆粒、正四邊形顆粒、正六邊形顆粒。首先以原始模型為基礎，在不改變模型中單個顆粒的面積和形心位置的情況下，將顆粒形狀分別轉化為相應的簡化形狀。經過初步轉化，一些靠近邊緣的顆粒會與模型邊界相交，為保證模型中顆粒位置的隨機性不變，將其與內部較小的顆粒進行位置交換。最終，得出了與原始模型具有相同顆粒密度和隨機性的三種簡化模型。其轉化結果如圖2所示。

圖2 不同顆粒形狀的簡化模型

1.4 網格劃分與邊界條件

如圖3所示，將原始模型以子模型的形式嵌入到尺寸遠大于原始模型的宏觀模型當中，模型均使用CPE3（3節點線形平面應變三角形單元）的單元類型進行網格劃分。通過對宏觀模型進行單向拉伸模擬，研究子模型的材料特性，及原始模型和三種包含不同顆粒形狀的簡化模型。

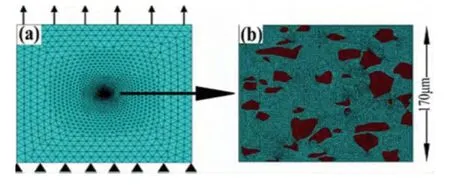
圖3 模型的邊界條件與網格劃分

2 結果與討論

圖4 不同形狀顆粒模型的應力-應變曲線

如圖4為含有不同顆粒形狀模型的應力-應變曲線。圖中，它們在彈性階段幾乎重合，并且具有著非常相似的應變硬化和應變率硬化趨勢。可以看出，顆粒形狀的改變，并沒有對復合材料的彈性參數有所影響。而在材料的應變硬化階段，發現圓形顆粒與正六邊形顆粒模型的預測應力較低，而正四邊形顆粒模型的預測應力最大并略高于原始模型。

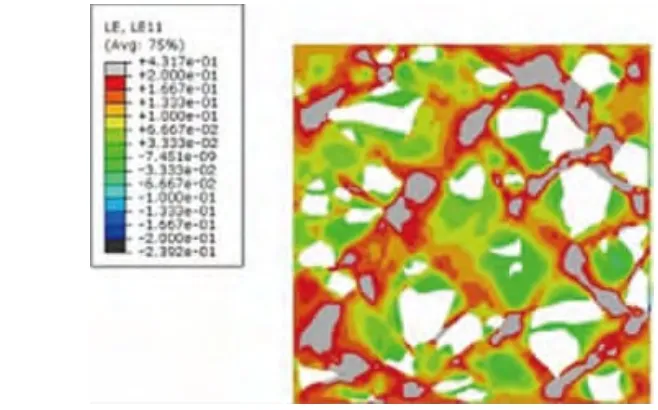
圖5 原始模型的應變云圖

圖6 包含正方形顆粒與圓形顆粒模型的應變云圖

通過對比，如圖5、圖6所示三種模型發現，模型中均顯示出了沿加載45°方向較大的塑性變形帶，但含有正四邊形顆粒模型中的失效區域（灰色區域）要明顯多于圓形顆粒模型，并且在所有模型中均可發現，模型中的失效區域多集中于顆粒棱角處以及顆粒較為密集的區域。而從含有正四邊形顆粒的簡化模型與原始模型對比看出，原始模型中基體的應變分布則顯得更為均勻。

規律總結得出，通過使用圓形、正六邊形等較為圓滑的簡化顆粒模型對復合材料進行有限元模擬計算，其計算結果準確度較低，這是由于該種簡化模型中顆粒與基體的接觸面積較小，以及圓滑的顆粒形狀使得金屬基體有著相對較高的流動性，造成顆粒對基體的約束能力降低，顆粒能夠吸收的應力減少，因而表現出的增強效果較原始模型會有所降低，但值得關注的是其因此產生的應變分布的均勻性以及較低的應變損傷。雖然具備棱角要求的正四邊形顆粒表現出的增強效果、失效面積均與原始模型較為接近，但含正四邊形顆粒的模型中基體的應變分布較原始模型相比，其失效區域則顯得的較為集中，這是由于正四邊形相對于原始的不規則形狀，其棱角過于尖銳，應力集中現象過于明顯造成的。

3 結論

3.1 形狀圓滑的簡化模型，會使模擬結果在各方面均存有較大誤差，而類似于正四邊形的含有棱角的簡化模型，其模擬的應力-應變曲線雖然與原始模型較為接近，但其應變分布情況與原始模型仍然存有較大誤差。

3.2 由于不同顆粒形狀的簡化模型對SiCp/Al復合材料的彈性參數沒有影響并且其表現出的應變硬化和應變率硬化趨勢較為相似，該方法在研究顆粒密度、分布情況對復合材料力學性能的影響、規律總結上能夠起到簡化模型的作用，但在精確計算參數等方面，其不具有可行性。

[1]Yuan M N, Yang Y Q, Li C et al. Numericalanalysis of the stress-strain distributions in the particle reinforcedmetal matrix composite SiC/6064Al [J]. Materials and Design,2012, 38∶1～6.

[2]原梅妮,楊延清,李茂華等.金屬基復合材料多尺度計算方法研究進展[J]. 材料導報,2012 年,26(9)∶134～137.

[3]Zhang P, Li F G. Microstructure-based Simulation ofPlastic Deformation Behavior of SiC Particle Reinfored AlMatrix Composites, Chinese Journal of Aeronautics[J], 2009, 22∶663～669.

[4]L.L. Mishnaevsky Jr. Three-dimenisonal numbericaltesting of microstructures of particle reinforced composites [J],Acta Materialia, 2006, 52(14)∶4177～4188.

[5]Wang J C, The simulation of damping capacity ofSiCp/Al composites [D]. Northwestern Ploytechnical University,1991.