蟻群算法在求解TSP問(wèn)題中的改進(jìn)研究
王寶生,屈寶存
(遼寧石油化工大學(xué) 遼 寧 撫 順 1 13001)
旅行商問(wèn)題(Traveling Salesman Problem,TSP)是一個(gè)易于描述卻難以處理的NP-HARD問(wèn)題。近年來(lái),它引起了許多學(xué)者的廣泛關(guān)注。旅行商問(wèn)題不僅具有很重要的理論價(jià)值,而且還具有廣泛的實(shí)際應(yīng)用價(jià)值,如機(jī)器人路徑規(guī)劃、電路板設(shè)計(jì)、城市管道鋪設(shè)優(yōu)化、交通運(yùn)輸以及物流配送等領(lǐng)域都可視為TSP問(wèn)題的具體應(yīng)用。對(duì)于旅行商問(wèn)題,目前常用的方法有模擬退火算法、遺傳算法、神經(jīng)網(wǎng)絡(luò)法等。
蟻群優(yōu)化算法是模擬自然界中真實(shí)蟻群的覓食行為而形成的一種模擬進(jìn)化算法。它是一種新興的仿生學(xué)優(yōu)化算法,屬于元啟發(fā)算法的一種。它具有采用分布式并行計(jì)算機(jī)制、易于與其他方法結(jié)合、具有較強(qiáng)的魯棒性等優(yōu)點(diǎn),但其搜索時(shí)間長(zhǎng)、易陷于局部最優(yōu)解是其最突出的缺點(diǎn)。因此,既要使得蟻群算法的搜素空間盡可能的大,以尋找那些可能存在最優(yōu)解的解空間,同時(shí),又要充分利用螞蟻體內(nèi)當(dāng)前所有的有效信息,使得蟻群算法搜索的側(cè)重點(diǎn)放在那些可能具有較高適應(yīng)值的個(gè)體所在的區(qū)間內(nèi),以較大的概率收斂到全局最優(yōu)解。因此,在“探索”和“利用”之間建立一個(gè)平衡點(diǎn)是蟻群算法研究的關(guān)鍵問(wèn)題之一。
為了克服蟻群算法的這些缺陷,使它的性能更好,研究者們探索了信息素殘留因子(1-ρ)、信息啟發(fā)式因子、期望啟發(fā)式因子、信息素強(qiáng)度、螞蟻數(shù)目等蟻群算法的影響因素,并進(jìn)行了改進(jìn)[1-3]。高尚提出了混沌蟻群算法,采用混沌初始化改善個(gè)體質(zhì)量和利用混沌擾動(dòng)避免搜素過(guò)程陷入局部極值,實(shí)驗(yàn)表明該算法提高了計(jì)算效率[4]。湯可宗等從參數(shù)的動(dòng)態(tài)調(diào)整、信息量的更新規(guī)則、局部搜索策略進(jìn)行相應(yīng)的改進(jìn),引入信息素平滑機(jī)制,實(shí)驗(yàn)表明該算法具有較好的收斂性和穩(wěn)定性,能夠克服算法中早熟和停滯現(xiàn)象的過(guò)早出現(xiàn)[5]。王峰峰等提出了在蟻群算法中植入遺傳算法,利用遺傳算法生成信息素的分布,克服了蟻群算法中搜索時(shí)間長(zhǎng)的缺陷,在蟻群算法尋優(yōu)中,采用交叉和變異的策略改善了TSP解的質(zhì)量,實(shí)驗(yàn)表明該算法是有效的[6]。蔡榮英等提出了迭代改進(jìn)蟻群算法,在構(gòu)造解的過(guò)程中,螞蟻始終記憶一個(gè)完整的解,并只接受能夠改進(jìn)解的候選城市,使用解的部分重構(gòu)策略來(lái)保持種群的多樣性,避免早熟收斂,實(shí)驗(yàn)表明該算法在更少的迭代次數(shù)中獲得更好的解[7]。其他學(xué)者也做出了相應(yīng)的改進(jìn)研究[8-10]。
文中提出一種改進(jìn)蟻群算法,該算法在初始位置選擇和信息素更新機(jī)制兩方面進(jìn)行改進(jìn),在相同參數(shù)下,改進(jìn)后的蟻群算法的搜索時(shí)間大大縮短,而且得到了更好的最優(yōu)解。將其應(yīng)用到旅行商問(wèn)題中,和其它兩種算法相比,其具有較好的搜索最優(yōu)解的能力,對(duì)新解不會(huì)過(guò)早的終止,探索新解的能力進(jìn)一步增強(qiáng)。
1 蟻群算法
1.1 蟻群算法的步驟
在求解TSP問(wèn)題中,蟻群算法的具體實(shí)現(xiàn)步驟如下:
1)參數(shù)初始化。其中,令時(shí)間t=0,循環(huán)次數(shù)Nc=0,最大循環(huán)次數(shù)表示為Ncmax;將m個(gè)螞蟻置于n個(gè)城市上,則有向圖上每條邊(i,j)的初始化信息量τij=const,其中const表示常數(shù),且初始時(shí)刻△τij=0。
2)循環(huán)次數(shù) Nc←Nc+1。
3)螞蟻的禁忌表索引號(hào)k=1。
4)螞蟻數(shù)目k←k+1。
5)螞蟻根據(jù)狀態(tài)轉(zhuǎn)移概率公式(1.1)計(jì)算的概率選擇城市 j 并前進(jìn)
6)修改禁忌表指針,即選則好之后將螞蟻移動(dòng)到新的城市,并把該城市移動(dòng)到該螞蟻個(gè)體的禁忌表中。
7)若集合C中城市未遍歷完,即k 8)根據(jù)公式(2)和式(3)更新每條路徑上的信息量。 9)若滿足結(jié)束條件,循環(huán)次數(shù)Nc>Ncmax,則循環(huán)結(jié)束并輸出程序計(jì)算結(jié)果,否則清空禁忌表并跳到第2)步。 α為信息啟發(fā)式因子,表示軌跡的相對(duì)重要性,反映了螞蟻在運(yùn)動(dòng)過(guò)程中所積累的信息在螞蟻運(yùn)動(dòng)時(shí)所起的作用,其值越大,則該螞蟻越傾向于選擇其他螞蟻經(jīng)過(guò)的路徑,螞蟻之間協(xié)作性越強(qiáng);β為期望啟發(fā)式因子,表示能見度的相對(duì)重要性,反映了螞蟻在運(yùn)動(dòng)過(guò)程中啟發(fā)信息在螞蟻選擇路徑中的受重視程度,其值越大,則該狀態(tài)轉(zhuǎn)移概率越接近于貪心規(guī)則;ηij(t)為啟發(fā)函數(shù),其表達(dá)式為為相鄰兩個(gè)城市之間的距離。 t+n時(shí)刻在路徑(i,j)上的信息量按如下規(guī)則進(jìn)行調(diào)整 : 式中,ρ為信息素?fù)]發(fā)系數(shù),1-ρ為信息素殘留因子,為了防止信息的無(wú)限積累,ρ的取值范圍為次循環(huán)中路徑(i,j)上的信息素增量,初始時(shí)刻為第k只螞蟻在本次循環(huán)中留在路徑(i,j)上的信息量。 1)初始位置的缺點(diǎn) 在蟻群算法中,螞蟻初始位置的選擇是隨機(jī)性的,這樣可能造成螞蟻的分布過(guò)于密集。在初始搜索時(shí)螞蟻依據(jù)城市間的路徑信息來(lái)選擇下次的搜索路徑,使得螞蟻都傾向于選擇在自己附近較短的路徑,這樣造成了局部收斂過(guò)快,得到較小范圍的解空間,對(duì)求解結(jié)果造成影響。 2)在信息素機(jī)制方面存在的缺點(diǎn) ①算法初始化之后,螞蟻初始化位置是隨機(jī)選擇的,和各個(gè)城市間分布了相同的信息素初始濃度,這就造成了算法在開始搜索時(shí)的方向不確定性和求解的多樣性方面先天不足。 ②在螞蟻搜索過(guò)程中,信息素僅僅在所有螞蟻完成本次巡游時(shí)才會(huì)進(jìn)行全局更新,從而造成搜索時(shí)間過(guò)長(zhǎng)。 由于蟻群算法存在以上的缺點(diǎn),文中從以上兩個(gè)方面進(jìn)行改進(jìn),使其全局性與收斂速度都有明顯的提高。 對(duì)于初始化位置的確定,文中提出一種“螞蟻邊緣化”的初始位置選擇策略對(duì)初始位置進(jìn)行優(yōu)化。 此邊緣化的思想是將螞蟻放在所有城市的邊界位置,盡量打散螞蟻的密集點(diǎn),這樣在初始時(shí)刻,螞蟻相互之間不會(huì)過(guò)早的影響。判斷一個(gè)離散區(qū)域的邊界位置是很困難的,因?yàn)樗惶峁└鱾€(gè)城市的坐標(biāo)信息,這些坐標(biāo)信息直接可以得到任意兩城市的距離信息,這些信息只是一些抽象的數(shù)據(jù),對(duì)于尋找城市的邊界信息是不夠的。這里提出一種近似的方法來(lái)確定邊緣城市。 此方法根據(jù)實(shí)際城市間距離的數(shù)據(jù)信息,將某城市和其他城市間的距離信息全部相加和為Si,將Si按照從大到小的次序排列,根據(jù)Si的大小判斷,最大的Si是離其他城市最遠(yuǎn)的城市對(duì)應(yīng)的和,其主要思想如下所示: 1)設(shè)有m只螞蟻要選擇初始位置,先將n個(gè)城市分別求出與其他城市間的距離之和將得到的Si按照從大到小順序排序; 2)即可確定最大的Si對(duì)應(yīng)的城市即為距離其他城市最遠(yuǎn)的,其他依次次之; 3)將螞蟻放在前m個(gè)Si對(duì)應(yīng)的城市上,就實(shí)現(xiàn)了城市邊緣化的選擇。 在基本蟻群算法中,分別應(yīng)用初始位置邊緣化和初始位置隨機(jī)選擇,比較2種方法的優(yōu)劣。此處,城市規(guī)模為29,螞蟻數(shù)目為14,最大迭代次數(shù)為100,選取10次循環(huán)的平均值,α=1,β=5,ρ=0.7。 兩種方法的最后結(jié)果如表 1 所示。 表1 兩種初始化螞蟻算法的比較Tab.1 The comparison of two kinds of initialization ant algorithm 再次驗(yàn)證螞蟻數(shù)目不同的情況下,兩種方法的性能優(yōu)劣。 城市規(guī)模 48,螞蟻數(shù)目分別為 12、24、36、48,最大迭代次數(shù)1 000,選取10次循環(huán)的平均值,,。應(yīng)用兩種方法的最后結(jié)果如表2所示。 表2 不同螞蟻數(shù)目下兩種方法的比較Tab.2 The comparison of the two methods under different number of ants 實(shí)驗(yàn)結(jié)果分析如下: 1)通過(guò)表2看出,邊緣法比隨機(jī)法得到了更好的最優(yōu)解均值,從最優(yōu)解和最差解的差值可以看出,邊緣法的魯棒性更好。 2)通過(guò)表2的對(duì)比比較,當(dāng)螞蟻數(shù)目增加時(shí),邊緣法仍然比隨機(jī)法得到更好的解,但是,兩種方法得到的解的差別隨著螞蟻數(shù)目的增加越來(lái)越小,這是因?yàn)椋S著螞蟻的數(shù)目增加,越來(lái)越多的城市上被放置了螞蟻,兩種方法之間的差異逐漸減小,直到城市數(shù)目與螞蟻數(shù)目相同時(shí),兩者之間再無(wú)差別,同時(shí),算法搜索時(shí)間也會(huì)隨著螞蟻數(shù)目的增多而變長(zhǎng)。 由以上分析可知,利用邊緣法確定螞蟻初始化位置確實(shí)強(qiáng)于隨機(jī)方法,對(duì)于要巡游的城市規(guī)模較大、搜索速率要盡可能快時(shí),可以選擇邊緣法,同時(shí)將螞蟻數(shù)目為城市數(shù)目的3/4或者 1/2。 信息素在蟻群算法中的作用關(guān)系到算法能夠最終順利找到最優(yōu)解的關(guān)鍵因素。信息素更新機(jī)制為螞蟻尋找最佳路徑提供了指導(dǎo),對(duì)于蟻群算法解決靜態(tài)組合優(yōu)化問(wèn)題和動(dòng)態(tài)組合優(yōu)化問(wèn)題這都是非常必要的。 本文對(duì)信息素的更新規(guī)則做了一些改進(jìn)。首先,在初始化階段,對(duì)螞蟻初始化位置和各路徑上的信息素初始濃度分布按照某些規(guī)則進(jìn)行分配,使之符合實(shí)際情況。其次,將螞蟻局部的信息素更新和全局信息素更新結(jié)合使用,通過(guò)精英選擇策略,在候選解上的螞蟻完成一次巡游之后,對(duì)它附近路徑的信息素就進(jìn)行更新,其他路徑上的信息素不變化。 2.2.1 表格初始化信息素的分配的規(guī)范化 利用邊緣法可以對(duì)螞蟻初始化位置進(jìn)行選擇,可以考慮將搜索路徑上的初始信息素濃度分配按照下述規(guī)則進(jìn)行:在邊界的m個(gè)城市之間路徑上分配相同的信息素τ(0)=c;在余下的路徑上根據(jù)具體點(diǎn)的位置和求解問(wèn)題類型的不同,可以通過(guò)下述公式確定余下的n-m個(gè)點(diǎn)中的某點(diǎn)x處的初始信息素大小: 式中,i是距離城市x處最近的邊緣城市位置,k、a均是大于零的常數(shù),若為最小值問(wèn)題,則a>1;若為最大值問(wèn)題,則0 k、a的選擇應(yīng)以具體情況而定,即保證算法能夠在更接近真實(shí)環(huán)境下尋優(yōu)。 2.2.2 螞蟻全局路徑上信息素的改進(jìn) 在基本的蟻群算法中,螞蟻只有在一個(gè)搜索周期結(jié)束后,才能完成一次信息素的更新。對(duì)于所有螞蟻?zhàn)哌^(guò)的路徑,某些路徑上可能得到差的解,由于信息素的增加,此解可能變成假的最優(yōu)解;當(dāng)最優(yōu)解還沒(méi)走過(guò)時(shí),該路徑的信息素隨著蒸發(fā)量的變化變得越來(lái)越小,從而被忽略。則在下次搜索中,最優(yōu)解對(duì)應(yīng)的路徑被選取的概率越來(lái)越小,這樣造成了大量無(wú)效的搜索,使得運(yùn)算速度降低。 文中采用以下的信息素更新算法:在全局路徑上,假設(shè)L(t)是螞蟻搜索了t次之后所得到的最佳路徑,L*(t)是螞蟻未走過(guò)的路徑,對(duì)所有螞蟻?zhàn)哌^(guò)的路徑(i,j)∈Lk(t),t次尋優(yōu)結(jié)束后,位置i到j(luò)間的路徑信息素更新量為△τij(t): 螞蟻沒(méi)走過(guò)的路徑的信息素更新量為: 其中,γ∈(0,1),f(t)為 L(t)對(duì)應(yīng)的最佳目標(biāo)值。 對(duì)于全局螞蟻?zhàn)哌^(guò)的路徑,信息素的更新規(guī)則為: 對(duì)于螞蟻未走過(guò)的路徑的信息素更新規(guī)則為: 此規(guī)則減弱了已走過(guò)路徑的信息素更新速度,避免因?yàn)樾畔⑺卦黾舆^(guò)多而導(dǎo)致下次搜索的誤判,同時(shí)還增強(qiáng)了螞蟻未到達(dá)路徑的信息素更新速度,提高了搜素的效率。 以某物流配送中心的VRP系統(tǒng)為例驗(yàn)證算法的效果,假設(shè)2輛載貨車的載重量8 T,向8個(gè)顧客送貨,顧客對(duì)貨物需求量為 gi(i=1,2,…,8),每條配送路徑的花費(fèi)為 Ci,j(i,j=1,2,…,8),可得以下經(jīng)驗(yàn)數(shù)據(jù)如表3所示。 表3 物流配送中心配送路線成本表Tab.3 Distribution route cost table of logistics center 對(duì)蟻群算法和改進(jìn)信息素的蟻群算法對(duì)上述配送路線進(jìn)行優(yōu)化,找到一條最佳的配貨路線,即路程最短或者代價(jià)最小。 算法中參數(shù)設(shè)置如下:α=2,β=5,ρ=7,螞蟻數(shù)目 60,迭代10次,實(shí)驗(yàn)結(jié)果如表4所示。 表4 兩種蟻群算法的優(yōu)化結(jié)果比較Tab.4 The comparison of two kinds of ant colony algorithm optimization 改進(jìn)信息素蟻群算法最后求得的平均最優(yōu)值是67.5,選擇的最優(yōu)路線是:0-4-7-6-0-1-3-5-8-2-0,這比用基本蟻群算法求解得到的76.5要精確了很多,實(shí)驗(yàn)證明改進(jìn)算法在解決車輛路徑尋優(yōu)問(wèn)題具有很高的性能。 根據(jù)以上思想,該改進(jìn)的蟻群算法流程可描述如下: 1)參數(shù)初始化。其中,令時(shí)間t=0,循環(huán)次數(shù)Nc=0,最大循環(huán)次數(shù)表示為Ncmax。 根據(jù)邊緣法初始化螞蟻位置的思想,將m只螞蟻放在前m個(gè)Si對(duì)應(yīng)的城市上,此時(shí)有向圖上每條邊(i,j)的初始化信息量 τix(0)=ka-f(i-x)。 5)螞蟻根據(jù)狀態(tài)轉(zhuǎn)移概率公式(1)計(jì)算的概率選擇城市j并前進(jìn) 6)修改禁忌表指針,即選則好之后將螞蟻移動(dòng)到新的城市,并把該城市移動(dòng)到該螞蟻個(gè)體的禁忌表中。 7)若集合C中城市未遍歷完,即k 8)當(dāng)所有螞蟻完成本次搜索后,根據(jù)式(5)、(6)、(7)、(8)進(jìn)行全局信息素更新。 9)若滿足結(jié)束條件,循環(huán)次數(shù)Nc>Ncmax,則循環(huán)結(jié)束并輸出程序計(jì)算結(jié)果,否則清空禁忌表并跳轉(zhuǎn)到第2)步。 為了檢驗(yàn)算法的有效性和優(yōu)越性,分別將基本蟻群算法、遺傳算法、改進(jìn)的蟻群算法應(yīng)用于31個(gè)城市TSP問(wèn)題中進(jìn)行仿真實(shí)驗(yàn)。其中參數(shù)設(shè)置為:1)蟻群算法:螞蟻規(guī)模25,最大迭代次數(shù)1 000,信息素?fù)]發(fā)系數(shù)0.7,信息素啟發(fā)式因子1,期望值因子5。2)遺傳算法:種群規(guī)模100,最大迭代次數(shù)1 000,交叉率0.9,變異率0.1。將TSPLIB31中各個(gè)城市的坐標(biāo)給出,如圖1所示。 圖1 31個(gè)城市的坐標(biāo)Fig.1 The coordinates of 31 cities 通過(guò)仿真得: 1)基本蟻群算法的最短路徑,其示意圖如圖2所示。 圖2 基本蟻群算法Fig.2 Basic ant colony algorithm 其最終優(yōu)化路線為(數(shù)字代表TSP31城市坐標(biāo)的標(biāo)號(hào)):15-1-29-30-31-27-28-26-25-24-20-21-22-18-3-17-19-16-23-11-6-5-4-2-8-9-10-7-13-12-14。 2)遺傳算法的最短路徑,其示意圖如圖3所示。 圖3 遺傳算法最短路徑Fig.3 The shortest path of GA 其最終優(yōu)化路線為: 5-6-9-8-7-3-1-4-15-18-25-27-26-10-11-28-30-29-24-19-23-13-31-14-12-20-21-17-2-16-22。 3)改進(jìn)的蟻群算法的最短路徑,其示意圖如圖4所示。 圖4 改進(jìn)蟻群算法Fig.4 Improved ant colony algorithm 其最終優(yōu)化路線為: 14-12-13-11-23-16-5-6-7-2-4-8-9-10-18-1-17-19-3-24-25-20-21-22-26-28-27-30-31-29-15。 通過(guò)以上仿真,可以得到表5。 表5 利用幾種算法求解TSP31問(wèn)題的試驗(yàn)結(jié)果Tab.5 Experimental results of several algorithms for solving TSP31 分析以上實(shí)驗(yàn)數(shù)據(jù)可見,改進(jìn)后的蟻群算法具有較好的搜索最優(yōu)解的能力。如對(duì)TSP31在原有蟻群算法上的最短路徑為1.619e+004,改進(jìn)后的算法中得到的最短路徑為1.56e+004,在路徑演化過(guò)程中,改進(jìn)的算法對(duì)新解不會(huì)過(guò)早的終止,探索新解的能力優(yōu)化進(jìn)一步增強(qiáng)。同時(shí),在相同的參數(shù)下,改進(jìn)后的算法不僅迭代次數(shù)大大減少、優(yōu)化時(shí)間大大縮短,而且得到了更好的最優(yōu)解。實(shí)驗(yàn)表明,改進(jìn)后的算法具有較好的性能。 文中在蟻群算法的基礎(chǔ)上,通過(guò)對(duì)初始位置選擇、信息素初始化分配和全局信息素三方面的改進(jìn),將其應(yīng)用到求解TSP中,較有效的克服了蟻群算法中出現(xiàn)的搜索時(shí)間長(zhǎng)、易停滯、收斂速度較慢等問(wèn)題;從仿真結(jié)果來(lái)看,該算法在求解性能和時(shí)間性能方面都取得了很好的結(jié)果,從而實(shí)現(xiàn)了TSP問(wèn)題的優(yōu)化,為解決一些組合優(yōu)化問(wèn)題提供了一定的參考。 [1]Duan H B,Wang D B,Yu X F.Research on the optimum configuration strategy for the adjustable parameters in ant colony algorithm[J].Journal of Communication and Computer,2005,2(9):32-35. [2]葉志偉,鄭肇葆.蟻群算法中參數(shù)設(shè)置的研究-以TSP為例[J].武漢大學(xué)學(xué)報(bào),2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Research on the ant colony algorithm parameter settings-to TSP Case[J].Wuhan University,2004,29(7):597-601. [3]詹士昌,徐婕,吳俊.蟻群算法中有關(guān)算法參數(shù)的最優(yōu)選擇[J].科技通報(bào),2003,19(5):381-386.ZHAN Shi-chang,XU Jie,WU Jun.Ant colony algorithm,the optimal choice of algorithm parameters related[J].Technology,2003,19(5):381-386. [4]高尚.解旅行商問(wèn)題的混沌蟻群算法[J].系統(tǒng)工程理論與實(shí)踐,2005,25(9):100-104.GAO Shang.Chaos ant colony algorithm for traveling salesman problem[J].Systems Engineering Theory and Practice,2005,25(9):100-104. [5]湯可宗,江新姿,張磊,等.一種求解旅行商問(wèn)題的改進(jìn)蟻群算法[J].華東理工學(xué)院學(xué)報(bào),2007,30(4):387-391.TANG Ke-zong,JIANG Xin-zi,ZHANG Lei,et al.Improved ant colony algorithm for solving traveling salesman problem[J].East China Institute of Technology,2007,30(4): 387-391. [6]王峰峰,王仁明,伍佳.求解TSP問(wèn)題的一種改進(jìn)蟻群算法[J].控制理論與應(yīng)用,2010,29(7):1-3.WANG Feng-feng,WANG Ren - ming,WU Jia.TSP problem an improved ant colony algorithm [ J].Control Theory and Applications,2010,29(7):1-3. [7]蔡榮英,王李進(jìn),吳超,等.一種求解旅行商問(wèn)題的迭代改進(jìn)蟻群優(yōu)化算法[J].山東大學(xué)學(xué)報(bào):工學(xué)版,2012,42(1):6-11.CAI Rong-ying,WANG Li-jin,WU Chao,et al.Solving Traveling Salesman Problem iterative improvement ACO[J].Shandong University :Engineering Science,2012,42(1):6-11. [8]陳永強(qiáng).人工蟻群算法及其在組合優(yōu)化中的應(yīng)用[D].哈爾濱:哈爾濱工業(yè)大學(xué),2003. [9]馬良,項(xiàng)培軍.螞蟻算法在組合優(yōu)化中的應(yīng)用[J].管理科學(xué)學(xué)報(bào),2001.4(2):32-36.MA Liang,XIANG Pei-jun.Ant algorithm in combinatorial optimization[J].Journal of Management Sciences,2001.4(2):32-36. [10]葉志偉,鄭 葆 .蟻群算法中參數(shù)α,β,ρ設(shè)置研究-以TSP為例 [ J ].武漢大學(xué)學(xué)報(bào),2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Ant colony algorithm parametersα,β,ρ,set - A case study TSP [J].Wuhan University,2004,29(7):597-601.

1.2 蟻群算法的缺點(diǎn)
2 改進(jìn)的蟻群算法
2.1 初始位置選擇


2.2 信息素更新規(guī)則的改進(jìn)

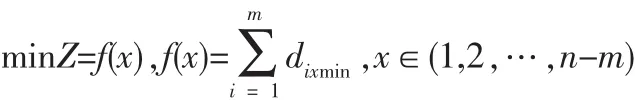






2.3 改進(jìn)蟻群算法的流程

3 改進(jìn)蟻群算法在TSP中的應(yīng)用



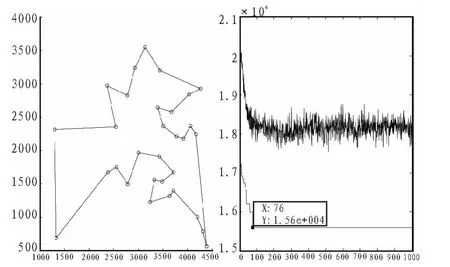
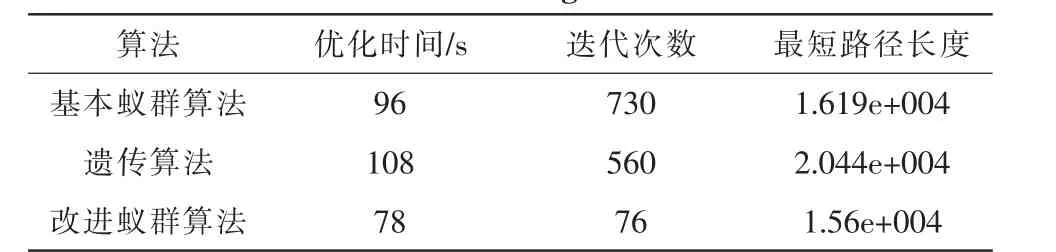
4 結(jié)論

