基于MEMS的數據手套傳感技術研究

王偉棟，費 潔，楊英東，錢 峰

（上海交通大學 電子信息與電氣工程學院，上海 200240）

人類與外界進行交互的過程中，手勢動作是最重要的方式方法，人們用手勢動作來表達思想，感知客觀世界，完成各種操作。數據手套是虛擬現實系統[1]中非常重要的設備，它可以跟蹤穿戴者靈活的手勢姿態，并實時地將其傳送至處理顯示系統。虛擬現實技術正在高速發展，并被廣泛使用，其中數據手套依托其自然高效的人機互動方式，更是在游戲娛樂、動畫設計、手術教學、手語識別、可視化科學研究、機器人控制、軍事情報等領域發揮著至關重要的作用。

傳統的手勢動作測量系統主要有機械式的和手套式的兩大類。機械式如Dextrious HandMaster（DHM），手套式如VPL公司的基于光纖原理的Data Glove等。 與傳統的傳感器技術相比，MEMS傳感器 （Micro-Electro-Mechanic System）具有體積小、重量輕、可靠性高、成本低、易于大規模生產等優點。近年來隨著MEMS技術的普及以及其價格的下降，MEMS擁有廣闊的工程應用前景，尤其是對小型運載體的導航制導與姿態控制具有重要意義。

文中采用集成封裝的MEMS三軸速率陀螺、MEMS三軸加速度計和MEMS三軸磁阻傳感器構成微慣性傳感器，它根據航姿解算的原理，解算出手勢姿態。基于MEMS的數據手套，穿戴方便，運動自由度大，抗干擾能力強，且不受光線條件的約束，不會出現光纖材料的疲勞損耗帶來的精度下降等問題，另外各傳感器相互獨立，利于維護，具有非常長的使用壽命。

1 手部運動學分析

1.1 人手結構

手部骨骼的主要組成部分是指節骨和關節，關節分為手掌關節和手指關節，如圖1所示。

圖1 人手骨骼結構Fig.1 Bone structure of hand

不同關節間的轉動決定手的姿態，包括指節骨繞其相應關節的左右側擺以及彎曲，具有很高的復雜度。其中，大拇指有5個自由度，其余四指各有4個自由度，加上手在空間的6個自由度，所以人手共有27個自由度。手的自然運動是一種有規律的運動，有著內在的約束條件：1）指關節的彎曲側擺范圍有限；2）手指的三段指骨的運動是處于同一個平面內;3）除拇指外，各手指末端關節的彎曲度是其前面關節的彎曲度的2/3[2]。

1.2 手指的運動速度

下表是在大量的實踐操作基礎上，通過加速度傳感器數據得到的最大角速度（以食指、大拇指為例）。

表1 不同動作下手指的角速度Tab.1 Finger’s angular velocity under different movements

2 姿態解算方法

2.1 四元數姿態算法

描述載體姿態的變化可以分解為載體的3次轉動。這3次轉動可以用數序方法描述成3個獨立的方向余弦矩陣。

定義姿態矩陣Cnb即載體坐標系到導航坐標系的變換矩陣，若繞Z軸轉動角度，繞Y軸轉動角度，繞X軸轉動角度，則從載體坐標系到參考坐標系可用如下矩陣描述:

為了避免奇點問題，采用四元素解算姿態角。坐標變換矩陣[3]為：

姿態矩陣的四元素的微分方程：

姿態矩陣速率

用四階龍格庫塔實現四元數的更新：

四元數姿態矩陣微分方程式只要解4個一階微分方程式組即可，其計算量與方向余弦姿態矩陣相比有明顯的減少，滿足實時性的要求[5]。

2.2 初始對準算法

在初始靜止狀態下，令加速度計的載體坐標系和運載體的載體坐標系重合，得到重力加速度在載體坐標系上的投影分量，分別記為 αbx，αby，αbz，那么：

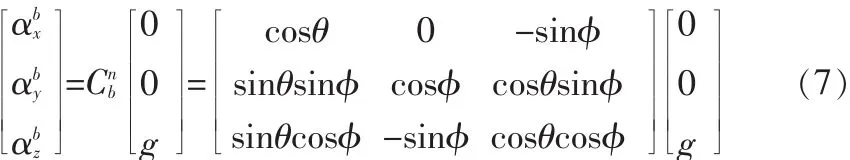
磁阻傳感器輸出的為磁場強度H在載體坐標系下3個軸上的投影分量，記為

地磁場水平分量指向的是地磁北極，可以利用ψ=arctan來確定北。由于磁北極與地理北極并不完全一致，故根據地理位置確定磁偏角對方向角進行修正。

2.3 擴展卡爾曼濾波

陀螺的隨機漂移會引起累計誤差，需要使用信息融合對誤差進行綜合校正。

對于本微慣性傳感器，其中非線性性質可能存在于過程模型中或者觀測模型中。為了進一步提高精度和可靠性，這里使用擴展卡爾曼濾波器（EKF）[6]。

擴展卡爾曼濾波中，狀態轉換和觀測模型并不要求是狀態的線性函數，替換的公式如下：

根據從之前的估計值，函數f可以計算預測的狀態，函數h也可以預測狀態下的測量值。不過，f和h不能直接應用于協方差當中，這里需要計算偏導矩陣。所以，擴展卡爾曼濾波器等式為：

預測階段：

使用偏導矩陣更新模型：

更新階段：

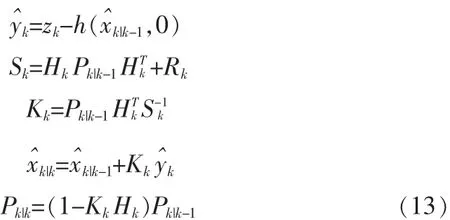
3 傳感器系統

數據手套傳感器系統由多個微慣性傳感器組合構成的傳感器網絡。每個微慣性傳感器由三軸MEMS陀螺、三軸MEMS加速度計和三軸磁阻型磁強計構成。三軸陀螺用于測量絕對角速率，與時間積分計算角度增量；三軸加速度計用于測量載體三個方向的加速度，計量水平方向的傾斜，同時有助于修正陀螺在俯仰和滾動方向的漂移；三軸磁阻型磁強計通過測量地磁強度，提供初始方向角同時修正航向角的漂移。為了減少突然的高強度磁場引起的不穩定性，這里采用S/R開關電路消除磁阻傳感器的漂移。需要說明的是，用于姿態解算的處理器與三種類型的傳感器一起集成于同一電路板中，即本文說提出的微慣性傳感器可以輸出解算好的姿態角以及原始的其內的各傳感器原始數據。

圖2 微慣性傳感器分布圖Fig.2 Distribution of micro inertial sensors

微慣性傳感器尺寸為12×20×5 mm，安置在手部的關節之間，尺寸滿足設計要求，不影響手部關節的正常活動。微慣性傳感器共6個，其中，5個微慣性傳感器安置于手指關節之間，用于檢測手部主要關節的彎曲角度，第6個傳感器集成在手背的嵌入式測控單元中，用于測量手掌的姿態。嵌入式測控單元通過IIC獲得各微慣性傳感器數據，實時處理，并與上位機通信，如圖2所示。

嵌入式測控單元包括了根據手部約束條件的判斷和數據的優化，這可以提高數據的準確性，并且減輕上位機的計算量。

4 實驗與測試

4.1 傳感器的標定

將傳感器固定在六面體內部，傳感器的坐標系與六面體棱邊對齊；將六面體的 x，y，z軸依次向上和向下放在水平面上，每一次向上或向下測量 2次，即繞法向旋轉 180°，這樣可以消除水平面的不平度對標定的影響，求二次平均值，測得各軸加速度計分別向上和向下共6組數據。

利用這六組數據，上位機標定解算軟件中通過最小二乘法求出加速度計零位、標度因子和交叉耦合項，并將解算參數燒錄到傳感器中，這個過程通過編制的軟件自動完成。

4.2 靜態測試

使用無磁標定平臺可對傳感器進行靜態測量，在測試前平臺由高精度傾角儀校準，確保水平面兩個軸向處于零位。基準邊也由指北儀校準，指向真北。

將數據全部通過串口輸出到PC中，得到俯仰、橫滾、航向角的靜態誤差，如圖3所示。

圖3 微慣性傳感器靜態誤差Fig.3 Static error of micro inertial sensors

可見，俯仰、橫滾的靜態誤差在0.1°，減去上海的確的磁偏角4.33°，航向角的靜態誤差為0.15°，符合要求。

4.3 動態測試

這里采用我們自己研發的弱磁雙軸電動轉臺對微慣性傳感器進行俯仰、橫滾的測量，它由內環橫滾軸框架和外環俯仰軸框架組成，控制精度為±0.08°。微慣性傳感器固定在內環框中。

由于轉臺限定，這里分別測量 60°/s和 300°/s。 300°/s已可以覆蓋絕大部分的日常手勢動作。跟蹤能力見圖4、圖5、圖 6、圖 7。

圖4 俯仰角300°/s時的動態響應速度Fig.4 Dynamic response speed of Pitch under 60°/s

圖5 俯仰角300°/s時的動態響應速Fig.5 Dynamic response speed of Pitch under 300°/s

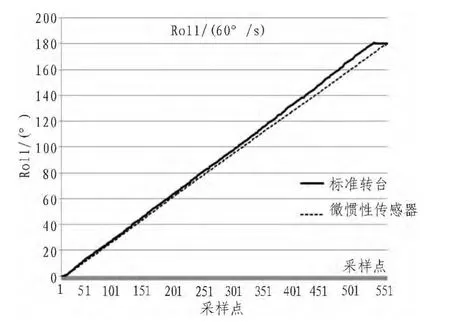
圖6 橫滾角60°/s時的動態響應速度Fig.6 Dynamic response speed of Roll under 60°/s

通過對比可知，微慣性傳感器與轉臺的曲線基本吻合，誤差較小，動態精度為2°，但有一定的時延，微慣性傳感器的內部更新頻率為100 Hz，延遲約為0.05 s左右。

由于條件限制所限，采用的轉臺具有弱磁性，沒有對方向角進行驗證，后續需采用無磁轉臺開展進一步的實驗。

5 結束語

圖7 橫滾角300°/s時的動態響應速度Fig.7 Dynamic response speed of Roll under 300°/s

通過實驗，本文提出的基于MEMS制作的微慣性傳感系統，其姿態角度分辨率為0.05°，靜態精度為0.1°，動態精度為2°，角速率最高可達到 1 200°/s，采樣頻率可達 100 Hz，基本能夠滿足數據手套對傳感器的要求。目前市場上的5DT Data Glove 5最大采樣頻率60 Hz，動態測量精度1°，分辨率0.2°。本文提出的基于MEMS微慣性傳感器的數據手套除動態精度指標略低以外的其他指標都優于該產品。

整套系統經過長時間的測試，沒有出現數據丟失的情況，表現出良好的穩定性。本文所述姿態解算方法以及用于測量手勢的微慣性傳感器整體系統的設計思想，可為數據手套研究和設計提供一種新的思路和方法。

[1]Spear，Brian．VirtualReality：PatentReview．World Patent Information[J]．2002，24（2）：103-109．

[2]Jintae Lee，Tosiyasu L.Kunii， Model-based analysis of hand posture[J].IEEE Computer Graphics and applications，1995，15（5）:78-85.

[3]秦永元.慣性導航[M].北京:科學出版社，2006.

[4]孫章國.基于ARM的航姿參考系統研究[D].上海:上海交通大學，2010.

[5]張榮輝，賈宏光，陳濤，等.基于四元數法的捷聯式慣性導航系統的姿態解算[J].光學精密工程，2008，16（10）：1963-1970.ZHANG Rong-hui，JIA Hong-guang，CHEN Tao，et al.Attitude algorithm of strapdown inertial navigation system based on the quaternion method[J].Optics and Precision Engineering，2008，16（10）：1963-1970.

[6]沈曉蓉，張海，范耀祖，等.微捷聯姿態系統的一種擴展卡爾曼濾波方法[J].北京航空航天大學學報，2007，33（8）:933-935.SHEN Xiao-rong，ZHANG Hai，FAN Yao-zu，et al.Extended Kalman filter method for micro strapdown inertial navigation system[J].Journal of Beijing University of Aeronautics and Astronautics，2007，33（8）:933-935.