三相LCL型并網逆變器的模型分析及解耦控制

包獻文，卓放，譚佩喧

（西安交通大學電氣工程學院，710049，西安）

近幾年，能源需求與環境問題促使新能源發電 技術得到了迅猛發展［1-2］。隨著新能源比重的不斷增加，電網公司對新能源發電的電能質量有了更嚴格的標準，要求其具有準確的功率調節能力，并可以應對電網調度或低電壓故障等［3］。因此，提高新能源并網裝置利用率、改善并網電流電能質量以及準確控制功率輸出等具有重要意義。

LCL型濾波器具有比L型濾波器更理想的高頻濾波效果，且體積和損耗均小于同等濾波效果的L型濾波器，從而常被應用于新能源并網發電系統。LCL型濾波器雖然具有較好的濾波效果，但給系統引入了LCL的諧振峰，影響系統的穩定性，增加了參數設計與電流環的控制難度［4-5］。在現有文獻中，針對LCL型并網逆變器的研究多是在同步旋轉坐標下進行的，忽略了模型中的高階項和耦合項，將平均模型小信號線性化以后分析系統性能［6-7］，并不能準確體現系統耦合項的具體特性。

L型并網逆變器可通過在電流調節器輸出量上附加解耦項，實現D軸與Q軸的獨立控制。對于LCL型并網逆變器，D軸與Q軸之間的耦合項較為復雜，傳統的單閉環控制方案無法實現完全解耦。針對LCL型并網逆變器的耦合問題，文獻［8］提出的應用反饋線性化理論設計的解耦方案，雖然理論上可以實現D軸與Q軸的完全解耦，但控制系統設計復雜，且控制器參數相互制約，影響控制效果。文獻［9］提出了一種模型降階法解決LCL型逆變器并網電流控制方案，但該方案沒有直接控制網側電感電流，其控制量與電網電壓存在一定的相位差，因此控制器需進行幅值和相位的補償。綜合目前的研究現狀，尚未有成熟的LCL型逆變器解耦控制方案。

針對上述問題，本文提出了一種LCL型并網逆變器的解耦控制策略，可以有效解決同步旋轉坐標下的耦合問題，且控制器設計簡單。本文方案的基本思想是：應用控制理論中的框圖等效變換原理，逐步消除每個濾波器元件D軸與Q軸之間的耦合項，并將所有解耦項移至控制器之后，得到系統總的解耦表達式，實現D軸與Q軸的完全解耦。仿真和實驗結果表明，與傳統的單閉環控制方案相比，本文提出的控制方法能有效解決D軸與Q軸的解耦問題，實現有功與無功的獨立控制，且系統具有良好的動態響應特性。

1 三相LCL型并網逆變器建模及分析

1.1 三相LCL型并網逆變器的建模

三相LCL型并網逆變器拓撲結構如圖1所示，圖中忽略了L1和L2的等效串聯電阻以及濾波電容Cf的阻尼電阻Rd。鑒于篇幅問題，文中直接給出同步旋轉坐標下LCL并網逆變器的平均模型如下

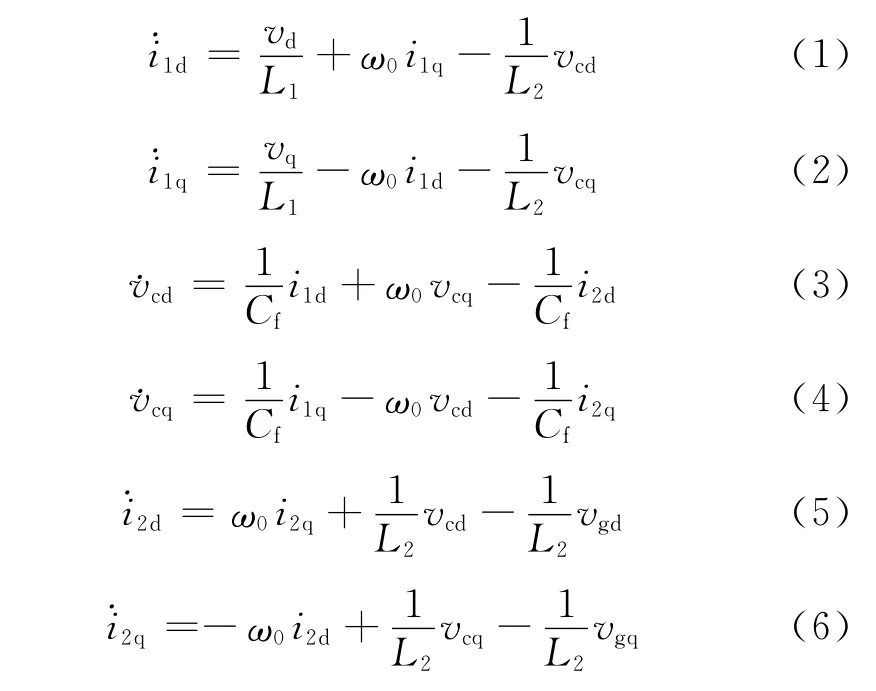
式中：ω0為電網角頻率，即坐標變換矩陣Tabc／dqo中的旋轉角頻率；下標d代表有功分量，下標q代表無功分量。詳細的建模過程可以參考文獻［10］。考慮到系統為三相三線制，不含有零序通路，因此在建模過程中省略了0軸。

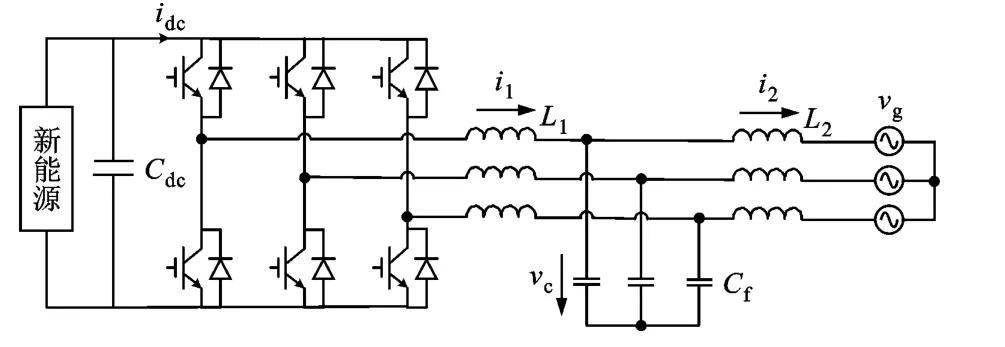
圖1 三相LCL型并網逆變器拓撲結構

1.2 三相LCL型并網逆變器的平均模型分析

由三相LCL型并網逆變器的模型可知，逆變器的平均模型相當于一個強耦合的兩輸入、兩輸出系統。各輸入、輸出變量之間的傳遞函數為

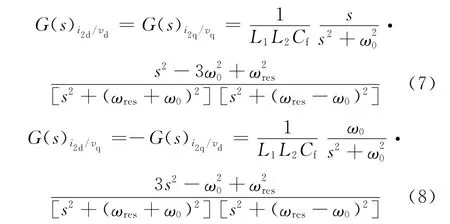
式中：ωres為LCL濾波器諧振頻率

傳遞函數式（7）對應的幅頻特性如圖2所示，由式（7）和圖2均可得出以下結論：

（1）通過坐標變換，D軸與Q軸具有相同的傳遞函數，交叉通道具有相似的幅頻特性；

（2）坐標變換引入了6個耦合項，難以實現D軸與Q軸的獨立控制；

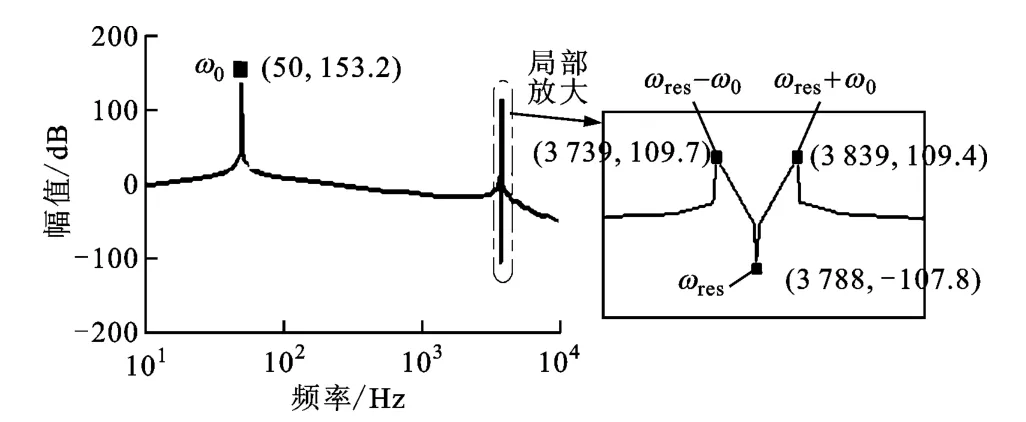
圖2 傳遞函數G（s）i2d／vd的幅頻特性

（3）坐標變換改變了原系統的諧振峰分布，使被控對象由單一的諧振峰ωres變為含有3個諧振峰的系統，新的諧振峰位于ω0、ωres±ω0處；

（4）LCL濾波器原有的諧振峰ωres在同步旋轉坐標下以局部極大值的形式存在。

1.3 平均模型的諧振峰特性分析

常見的諧振峰抑制方案有兩種［11］：一是無源阻尼控制，即在濾波回路中串聯或并聯電阻以增加系統的阻尼；另一種方案是有源阻尼控制，其本質是通過控制算法來實現阻尼作用。無源阻尼的控制方案簡單有效，因此本文分析了電感L1的等效串聯電阻R1、濾波電容Cf的阻尼電阻Rd和電感L2的等效串聯電阻R2對平均模型的諧振峰的具體影響。

1.3.1 L1的等效串聯電阻R1對諧振峰的影響

為了簡化分析過程，假設Rd=0，R2=0，單獨分析R1對系統平均模型的影響。為便于直觀分析，本文給出了R1變化時D軸通道傳遞函數幅頻特性的局部放大圖，分別位于ω=ω0和ω=ωres處，如圖3所示。

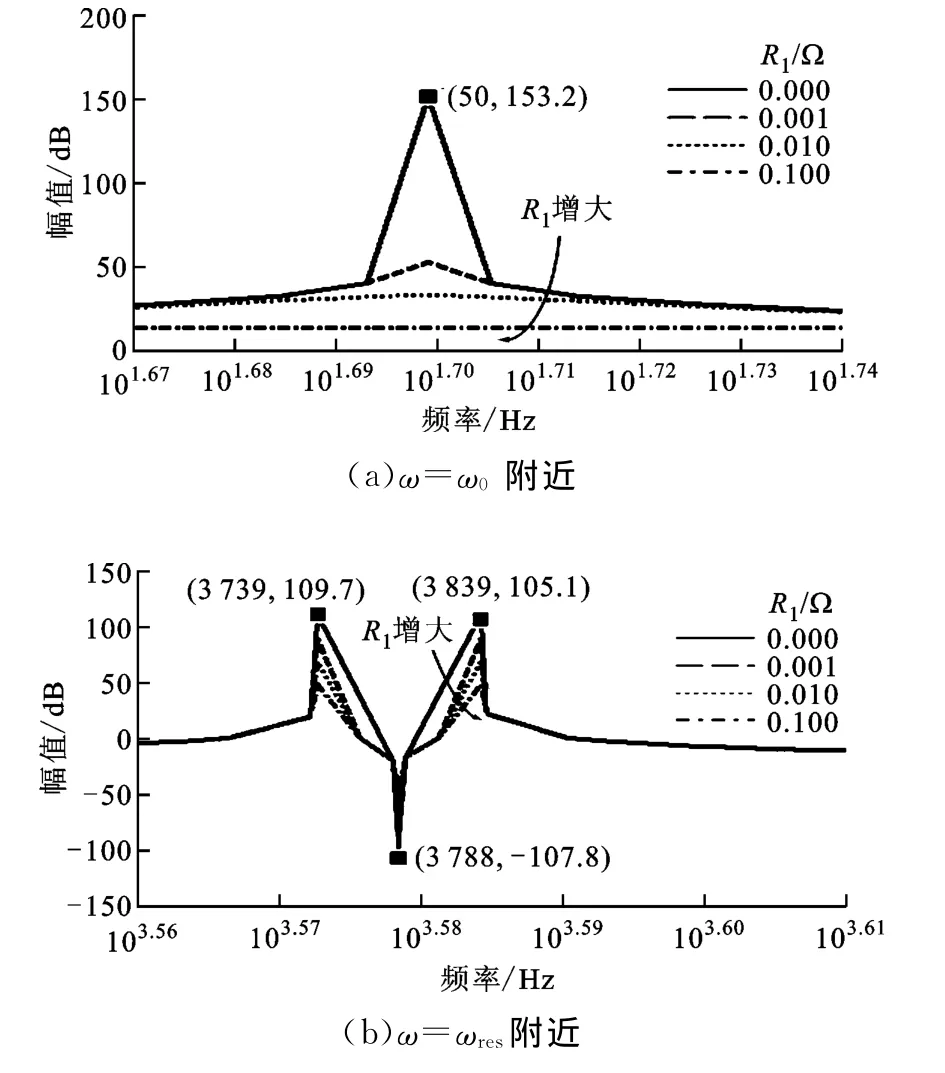
圖3 R1 變換時G（s）i2d／vd幅頻特性的局部放大圖

由圖3可知，R1的增加對ω=ω0處的諧振峰有明顯的抑制作用，但對ωres±ω0處諧振峰的抑制作用不明顯，同時不改變ωres處局部極大值的幅值。

1.3.2 Cf的阻尼電阻Rd對諧振峰的影響 假設R1=0，R2=0，單獨分析Rd對系統平均模型的影響。本文同樣給出了Rd變化時D軸通道傳遞函數幅頻特性的局部放大圖，如圖4所示。

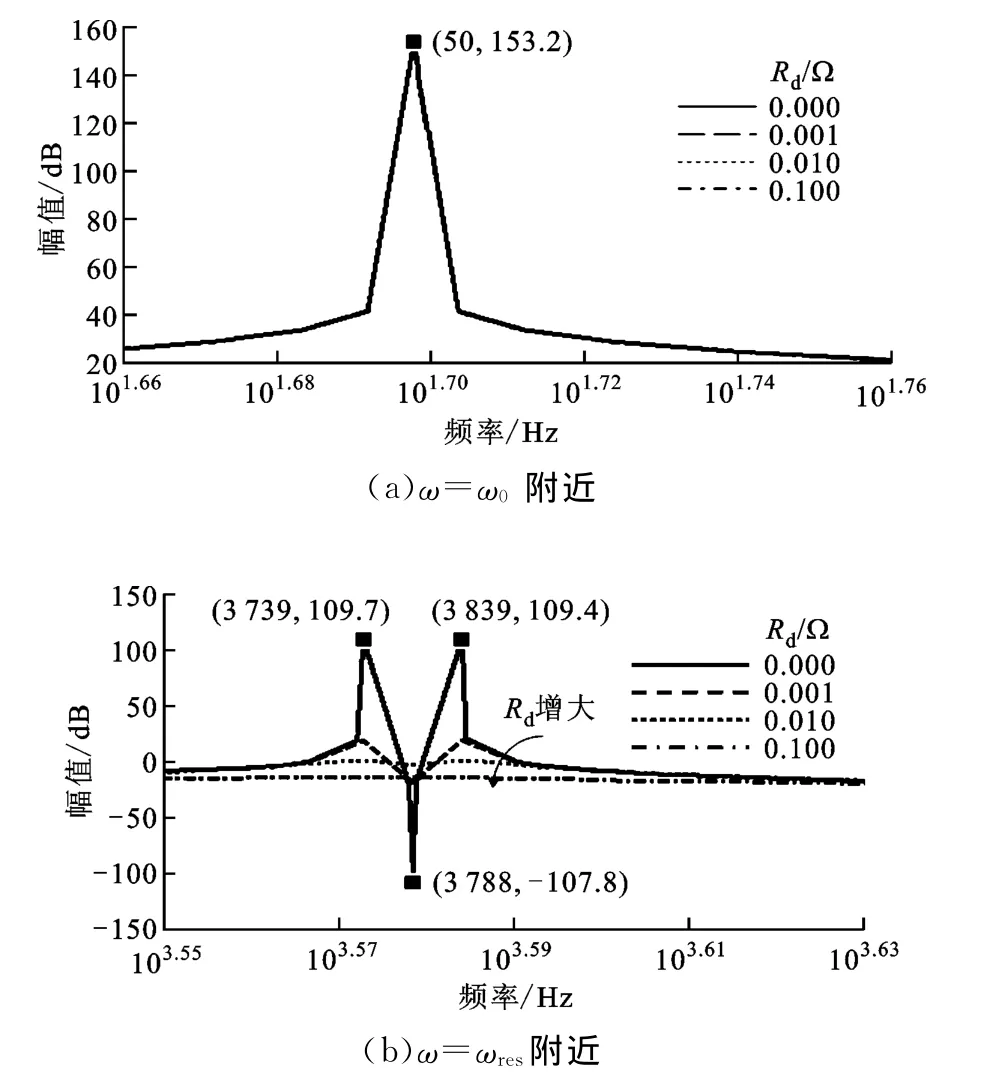
圖4 Rd 變換時G（s）i2d／vd幅頻特性的局部放大圖

由圖4可知，Rd的增加對ω=ω0處的諧振峰完全沒有抑制作用，但對ωres附近的諧振峰以及局部極大值都有明顯的抑制作用。同時，從整體的幅頻特性可以看出，Rd的增加對高頻幅值的抑制作用減弱了。

1.3.3 L2的等效串聯電阻R2對諧振峰的影響

假設R1=0，Rd=0，單獨分析R2對系統平均模型的影響。本文同樣給出了R2變化時D軸通道傳遞函數幅頻特性的局部放大圖，如圖5所示。

由圖5可知，R2的增加對ω=ω0處的諧振峰有很強的抑制作用，同時對ωres±ω0處諧振峰以及ωres處的幅值也都有明顯的抑制作用。從整體的幅頻特性可以看出，隨著R2的增加，整個系統的低頻幅值增加，對高頻的抑制作用不變。

綜合上述分析，3個電阻均可以在一定程度上抑制系統的諧振峰，R2對諧振峰的抑制效果最優，但并不能消除系統的耦合問題。針對該問題，下文提出了一種解耦控制策略。

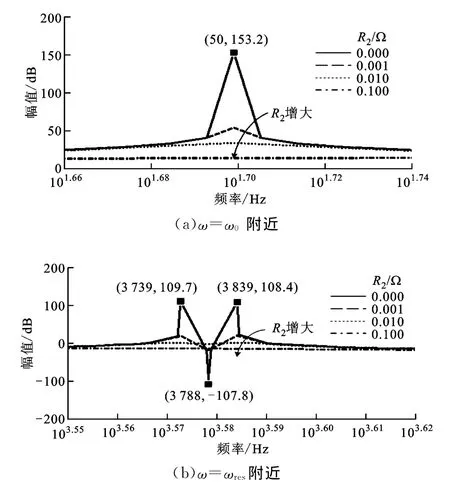
圖5 R2 變換時G（s）i2d／vd幅頻特性的局部放大圖

2 三相LCL型逆變器的解耦控制

本文針對三相LCL型逆變器的耦合問題，設計了精確解耦的控制方案，整個系統的解耦過程如圖6中虛線框所示。在逆變器的模型中，L1、Cf和L2均摻雜耦合項，因此按著L1、Cf和L2的次序依次解耦，并匯總為整體的解耦項。

圖6 LCL型逆變器的解耦框圖

（1）電感L1的解耦。電感L1的解耦如圖6中的實線框所示，D軸與Q軸類似，其中解耦項為

電感L1解耦后的化簡框圖如圖7所示。

（2）電容Cf的解耦。電容Cf解耦項如圖7中的實虛線框所示，其中

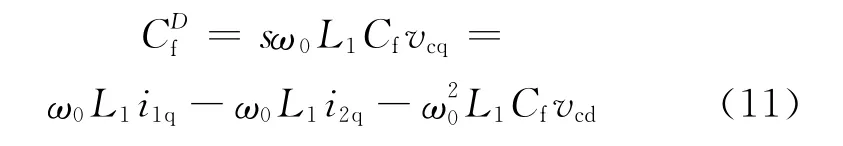
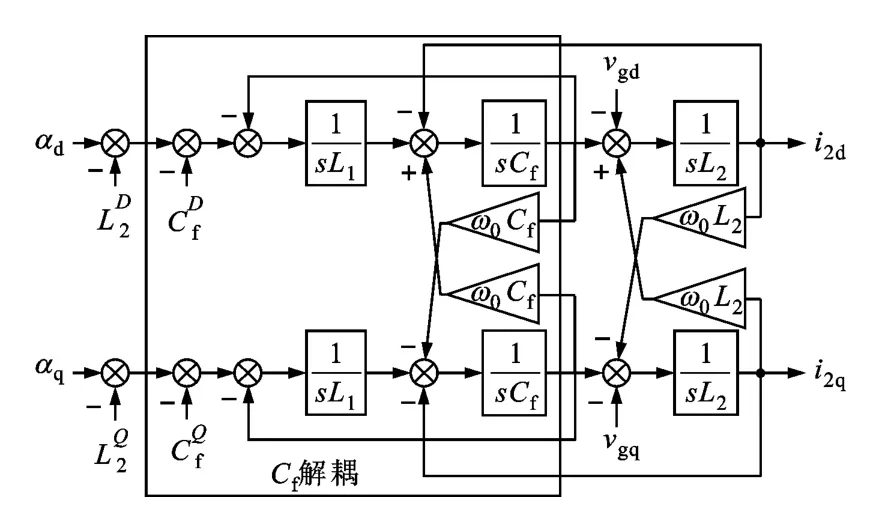
圖7 電感L1解耦后的化簡框圖

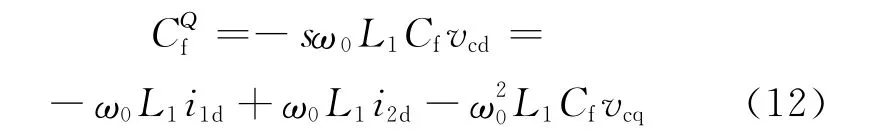
電感L1與電容Cf解耦后化簡框圖如圖8所示。

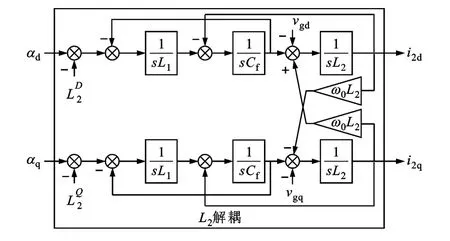
圖8 電感L1與電容Cf解耦后的化簡框圖

（3）電感L2的解耦。電感L2的解耦項如圖8中的實線框所示，電感L2的解耦涉及了比較點與引出點的交換，一般在控制框圖的等效變換中不常用這兩者的交換，因此將引出點部分作為前饋抵消掉。圖8中電感L2的解耦項為

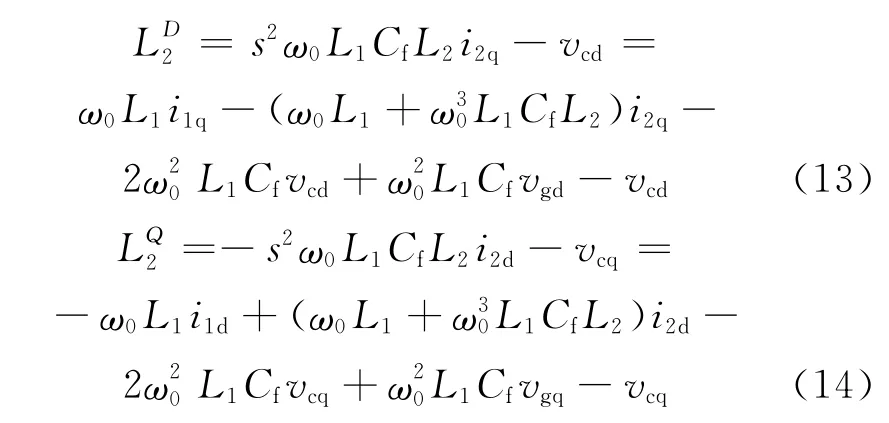
LCL濾波器完全解耦后化簡框圖如圖9所示。

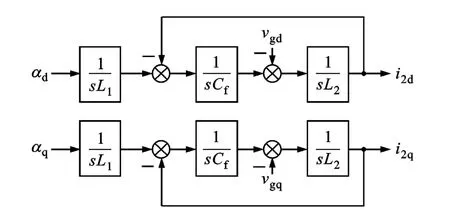
圖9 LCL濾波器全部解耦后的化簡框圖

綜合上述分析，匯總D軸與Q軸的解耦分項，得到D軸總的解耦項為

Q軸總的解耦項為

由圖9可以推導出網側電感電流與逆變器新的輸入變量之間的傳遞函數為

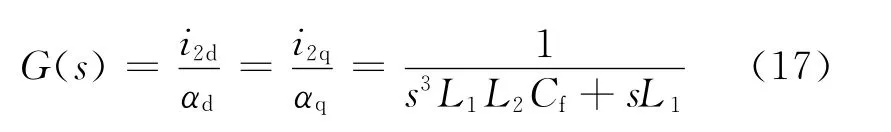
由式（17）可知，加入解耦項以后的被控對象，低頻體現一階特性，高頻為三階特性。因此，采用傳統的PI控制器加總的解耦項就可以實現D軸與Q軸的完全解耦，控制框圖如圖10所示。

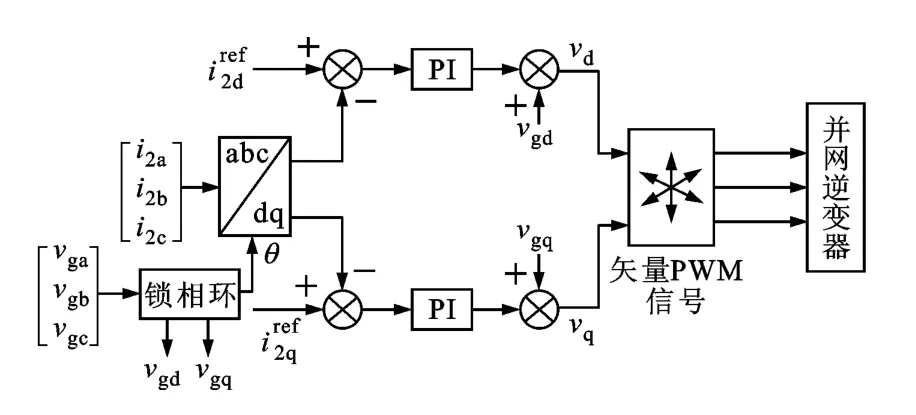
圖10 加入解耦項的控制框圖

3 系統仿真與實驗驗證

為了驗證本文提出的解耦控制方案的有效性，對該算法進行了仿真與實驗驗證，并與傳統單閉環控制方案做了對比研究，傳統的單閉環控制框圖如圖11所示。

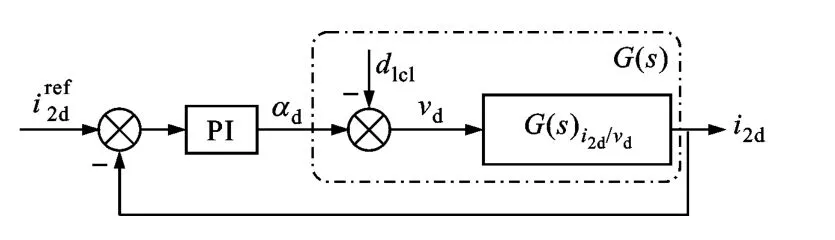
圖11 傳統的單閉環控制框圖

設計系統的額定功率為1kW，電網電壓有效值為22V，頻率為50Hz，直流母線電壓為80V，直流側支撐電容為3mF，開關頻率為10kHz，LCL濾波器的L1=1mH，Cf=90μF，L2=0.02mH。主電路利用電感L1和L2的等效串聯電阻抑制系統的諧振峰，沒有加入電容的阻尼電阻Rd。D軸與Q軸具有相同的控制器參數，kp=0.1，ki=100，對應的電流環帶寬大約為4kHz。

3.1 系統的仿真驗證

采用Matlab／Simulink軟件進行系統仿真，穩態運行時，輸出電流的諧波畸變率為0.66%。為了進一步說明本文提出的解耦方案的有效性，仿真了有功和無功電流指令階躍變化響應，并與傳統的不加解耦的控制方案作了對比研究，結果如圖12、圖13所示。由仿真結果可知，在不加入解耦項時，D軸與Q軸之間存在明顯耦合，當D軸（或Q軸）的控制量突變時，必然影響到Q軸（或D軸）控制量的變化；加入解耦項以后，當網側有功電流突變時，無功電流基本保持不變，反之亦然。仿真結果表明，本文所提的解耦控制方案實現了D軸與Q軸的完全解耦，且系統具有良好的動態特性。

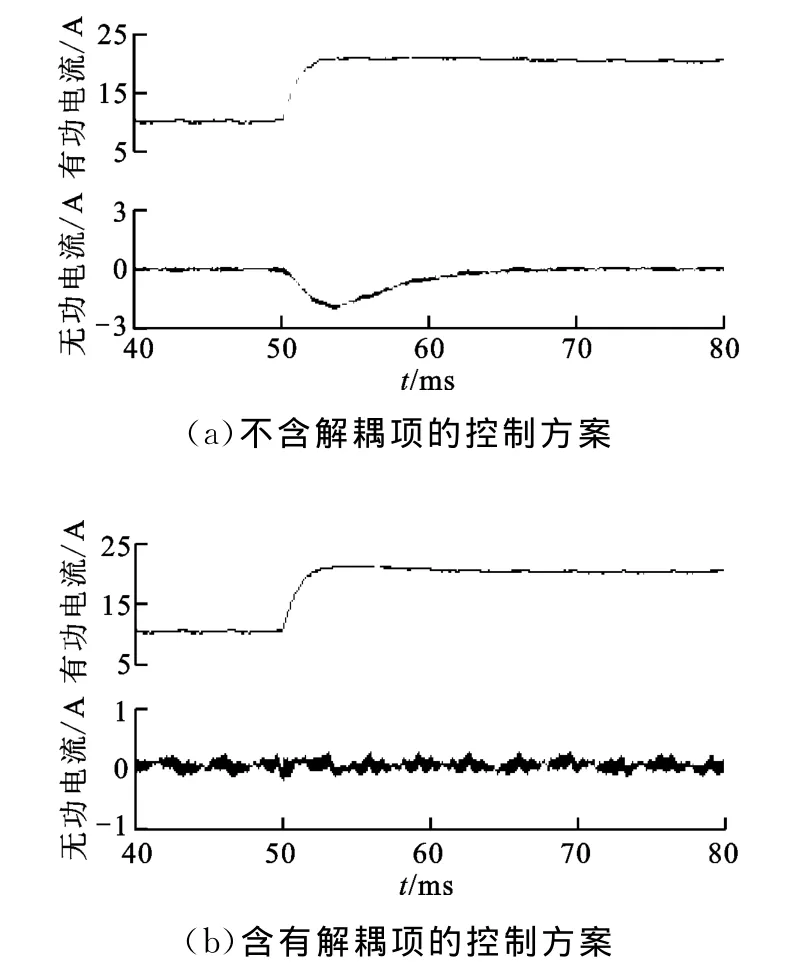
圖12 有功電流指令階躍變化時的并網電流波形

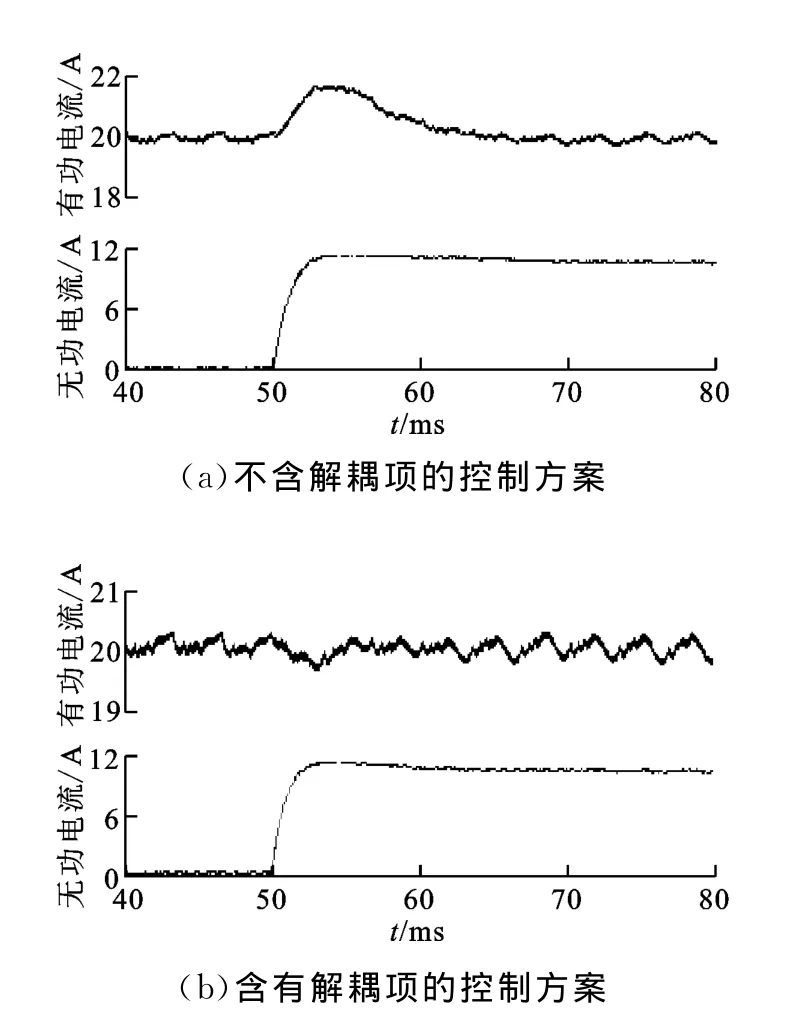
圖13 無功電流指令階躍變化時的并網電流波形

3.2 系統的實驗驗證

參照仿真系統的設計參數搭建了硬件實驗平臺，主控板控制器選用TI公司的TMS320F28335芯片，直流側選用Chroma可編程直流電源，IGBT模塊為英飛凌公司的FF150R12RT4，設計開關頻率為10kHz。當系統穩定運行時，電流給定幅值為17A，圖14為電網電壓及并網電流波形，表1為并網電流分析值，波形及分析值均由功率分析儀獲得。參照仿真情況，驗證了有功電流與無功電流的階躍響應，并與傳統的不加解耦的控制方案作了對比研究。波形采用CCS3.3的數據監視插件在線觀測，由于DSP的RAM空間有限，因此只記錄兩個工頻周期的數據，即為400個數據點，實驗結果如圖15、圖16所示。實驗結果再次驗證了本文提出的解耦控制方案的有效性。

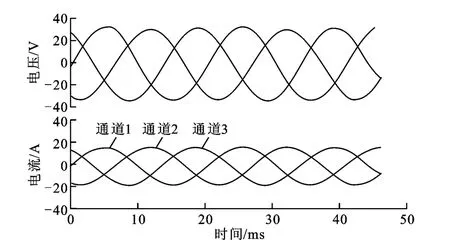
圖14 穩定運行時的電網電壓和并網電流波形圖

表1 穩定運行時的電網電流分析

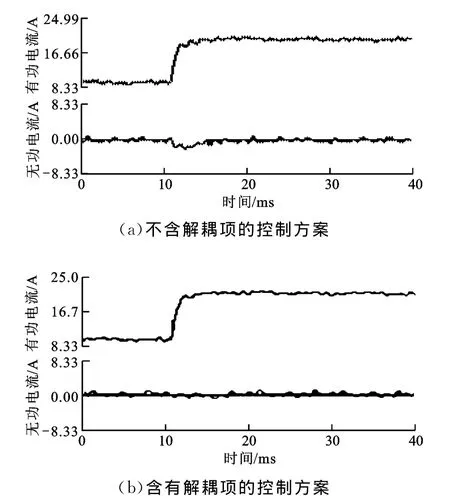
圖15 有功電流指令階躍變化時的并網電流實驗波形

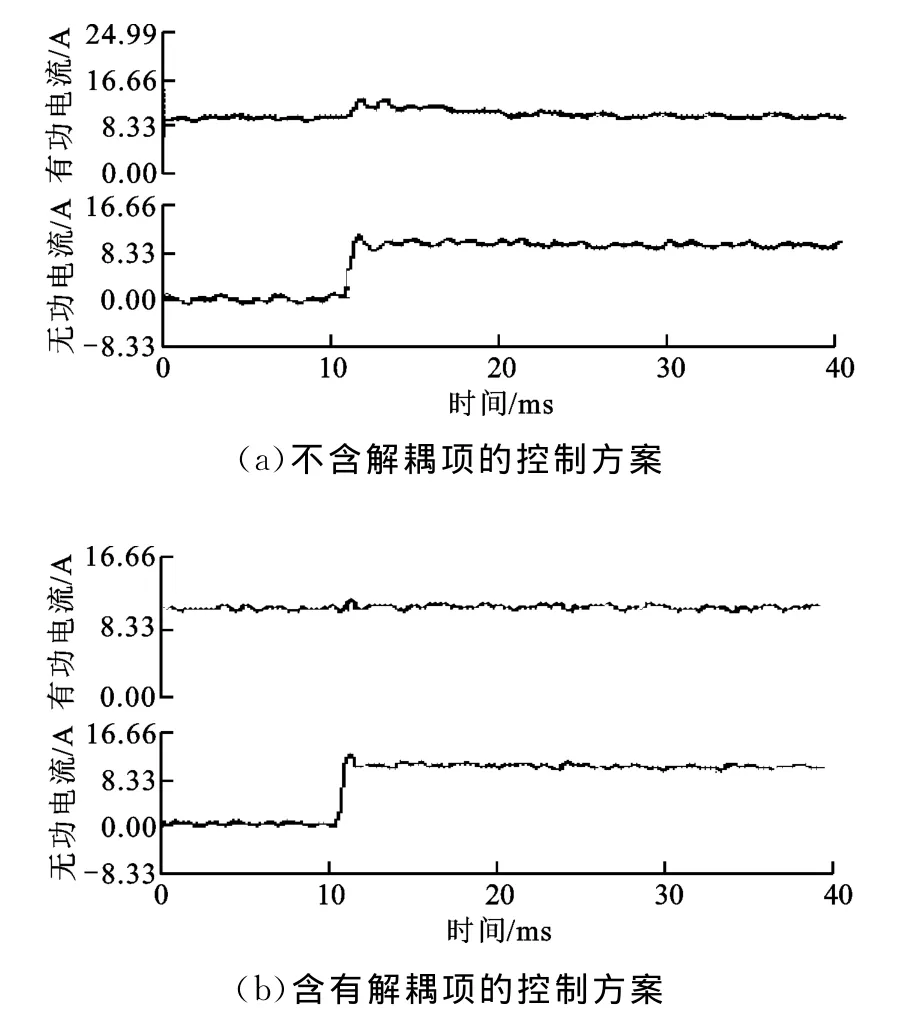
圖16 無功電流指令階躍變化時的并網電流實驗波形

4 結 論

本文建立了同步旋轉坐標下三相LCL型并網逆變器的平均模型，推導出系統的精確傳遞函數，揭示了坐標變換對原系統的影響，并分析了阻尼電阻對該模型諧振峰的抑制效果。針對該模型的耦合問題，本文提出了一種三相LCL型并網逆變器的解耦控制策略，并給出了詳細的解耦過程。仿真和實驗結果表明，與傳統的單閉環控制方案相比，本文提出的控制方法能有效解決D軸與Q軸的解耦問題，實現有功功率與無功功率的獨立控制，且系統具有良好的動態響應特性，可為新能源并網逆變器的精準功率控制提供技術保障。

［1］ MOHAMED A，ZHENGMING Z.Grid-connected photovoltaic power systems：technical and potential problems：a review ［J］.Renewable Sustainable Energy Reviews，2010，14（1）：112-129.

［2］ SOEREN B，JOHN K，FREDE B.A review of singlephase grid-connected inverters for photovoltaic modules［J］.IEEE Trans on Industry Applications，2005，41（5）：1292-1306.

［3］ SGCC.光伏電站接入電網技術規定.Q／GDW 617-2011［S］.北京：SGCC，2011.

［4］ MARCO L，FREDE B，STEFFAN H.Design and control of an LCL-filter-based three-phase active rectifier［J］.IEEE Trans on Industry Applications，2005，41（5）：1281-1291.

［5］ SHEN Guoqiao，XU Dehong，CAO Luping，et al.An improved control strategy for grid connected voltage source inverters with an LCL filter［J］.IEEE Trans on Power Electronics，2008，23（4）：1899-1906.

［6］ ZHANG Xiaotian，SPENCER J W，GUERRERO J M.Small-signal modeling of digitally controlled grid-connected inverter with LCL filters ［J］.IEEE Transactions on Industrial Electronics，2013，60（9）：3752-3765.

［7］ YANG Y，MEHRDAD K，VICTOR H.Modeling，control and implementation of three-phase PWM con-verters［J］.IEEE Trans on Power Electronics，2003，18（3）：857-864.

［8］ KHAJEHODDIN S，MASOUD K，PRAVEEN K，et al.A control design approach for three-phase grid-connected renewable energy resources［J］.IEEE Trans on Sustainable Energy，2011，2（4）：423-432.

［9］ HE Ning，XU Dehong，ZHU Ye，et al.Weighted average current control in a three-phase grid inverter with an LCL filter ［J］.IEEE Transactions on Industrial Electronics，2013，28（6）：2785-2797.

［10］EMILIO F，GABRIEL G，JESUS S，et al.Sensitivity study of the dynamics of three phase photovoltaic inverters with an LCL grid filter［J］.IEEE Transactions on Industrial Electronics，2009，56（3）：706-717.

［11］張興，曹仁賢.太陽能光伏并網發電及其逆變控制［M］.北京：機械工業出版社，2010：160-186.