談計算麥克勞林公式的間接法

張 輝，趙偉舟，敬 斌，李應岐

(第二炮兵工程大學 理學院, 陜西 西安 710025)

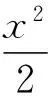
由函數的性質可得，這樣代換得到的等式(1)是成立的.但等式(1)是否就為ex2的麥克勞林公式呢？事實上，回答是肯定的，這就是所謂的間接法，而此方法現行教材往往并沒有給出理論證明.本文基于泰勒定理和高階導數理論，給出了計算兩類復合函數的麥克勞林公式的間接法，得到了一般性的結論，讓初學者靈活使用，達到事半功倍、舉一反三的效果.

1 預備知識

定理1[2]22-24若y=f(u)，u=φ(x)，其中f，φ具有n階導數，則

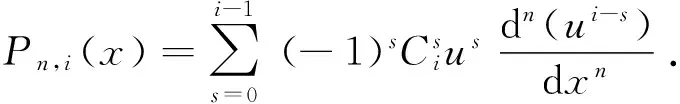
2 間接法

情形一：u=φ(x)=bx，b≠0.

若u=φ(x)=bx，則y=f(bx)，且有

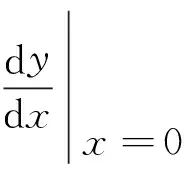
因此，復合函數y=f(bx)的帶有皮亞諾型余項的n階麥克勞林公式為

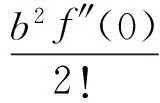
我們知道，函數y=f(x)的帶有皮亞諾型余項的n階麥克勞林公式為

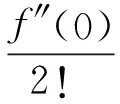
因此，y=f(bx)的麥克勞林公式(2)可由將函數y=f(x)的麥克勞林公式(3)中的x換成bx得到.

情形二：u=φ(x)=bxm，b≠0，m>1，m∈Z+.

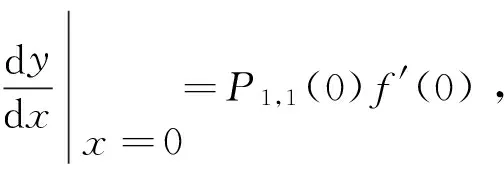
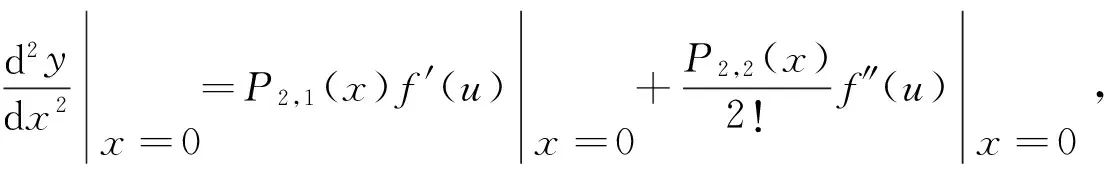
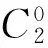
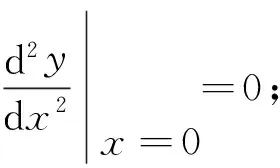
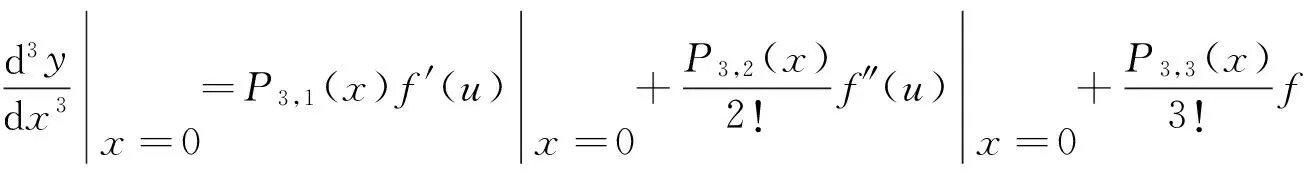
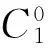
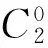
=[b33m(3m-1)(3m-2)x3(m-1)]|x=0=0.

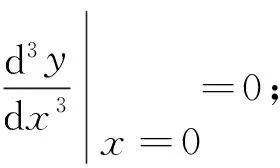
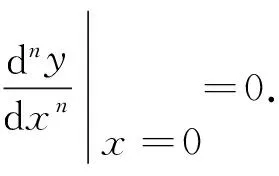
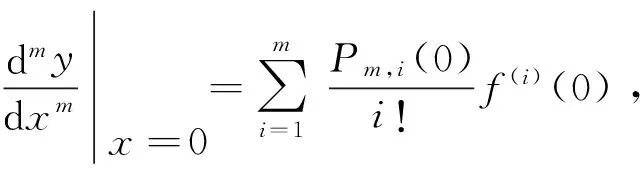
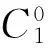
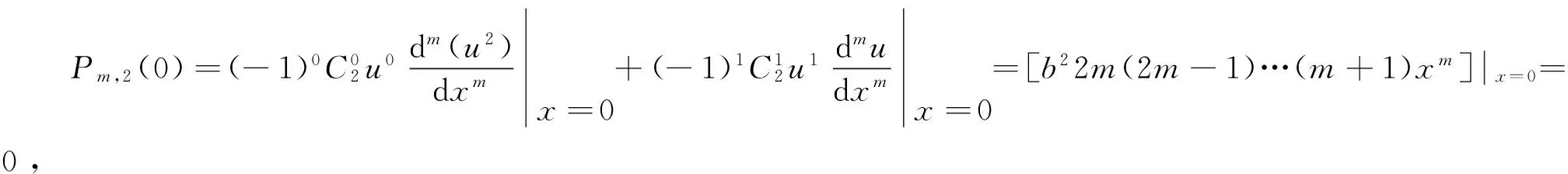
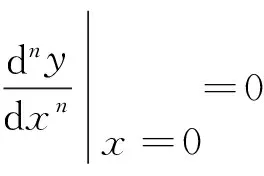
P2m,3(0)=…=P2m,m(0)=P2m,m+1(0)=…=P2m,2m(0)=0，

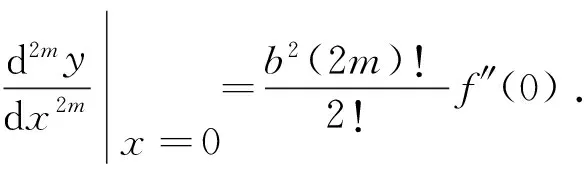
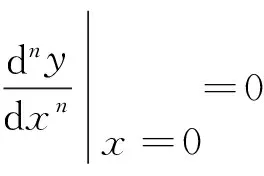
P(p+1)m,p+2(0)=P(p+1)m,p+3(0)=…=P(p+1)m,(p+1)m(0)=0，

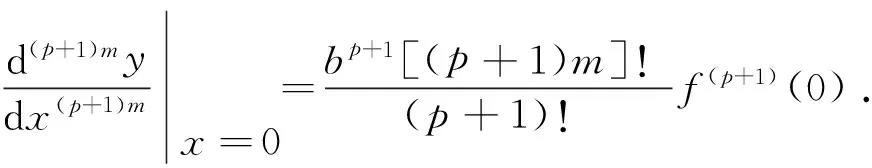
由泰勒中值定理[3]278-285可得，復合函數y=f(bxm)的帶有皮亞諾型余項的(p+1)m(p≥1,p∈Z+)階麥克勞林公式為

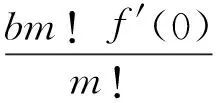
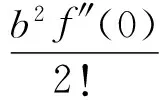
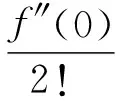
因此，函數y=f(bxm)的麥克勞林公式(4)可由將函數y=f(x)的麥克勞林公式(3)中的x換成bxm得到.

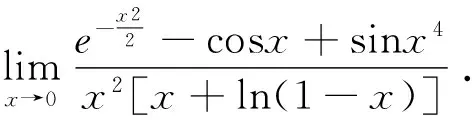
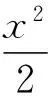
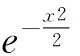
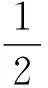
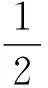
因此，

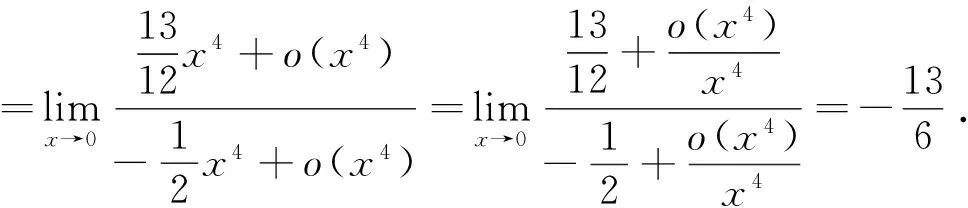
值得注意的是，對于一些特殊類型的函數，我們往往也可以借助于它的麥克勞林展開式[3]278-285來求解麥克勞林公式.例如，函數arctanx的麥克勞林展開式為

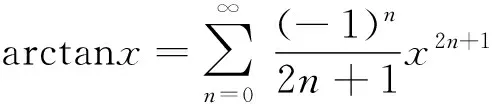
因此，arctanx的帶有皮亞諾型余項的2n+1階麥克勞林公式為

[1] 同濟大學數學系.高等數學(上冊·6版)[M].北京：高等教育出版社,2007.

[2] 陳世哲，陳仕洲.復合函數的高階導數公式及其應用[J].南陽師范學院學報，2010，9(12).

[3] 同濟大學數學系.高等數學(下冊·6版)[M].北京：高等教育出版社,2007.