基于改進型Smith預估器的超臨界機組主汽溫模糊控制系統

馬陽

（沈陽工程學院 自動化學院，遼寧 沈陽 110136）

目前，600 MW超臨界機組由于其主汽壓力和主汽溫度較高，提高了機組的熱效率和經濟性，已逐步成為我國電力行業的主力機組[1]。但主蒸汽溫度在實際運行中經常遇到頻繁、擾動量大的干擾，且汽溫控制對象具有時變性、非線性和大遲延等特點，因此應設計合理的主汽溫控制策略，以維持主汽溫的穩定，保證機組的安全運行和經濟效益。

大型火電機組控制過熱汽溫應用較為廣泛的是串級控制系統，其內回路為快速隨動系統，克服內擾的能力較強，但要求主、副調節器的參數必須配合好，才能得到理想的控制效果。由于汽溫對象的非線性和時變性，決定了控制器的最佳參數只適合于某一運行工況。當工況發生變化時控制器參數的匹配關系會變得不協調，進而影響控制效果。目前，模糊控制在工業控制中逐步得到應用，模糊控制的魯棒性和自適應能力較強，能夠很好的解決對象模型的不確定性、時變性和非線性問題，但對于汽溫對象的大遲延特性無法有效解決。Smith預估控制是克服對象大遲延的常用方法，但Smith預估器對模型的誤差十分敏感，魯棒性差，必須建立對象精確的數學模型才能有效解決時滯問題。

基于以上分析，本文提出了一種改進型Smith預估器對超臨界機組主汽溫對象惰性區特性進行預估補償，并將模糊控制理論與經典控制理論結合形成了主汽溫綜合控制方案。通過仿真研究證明這種汽溫綜合控制新方案能夠很好的克服主汽溫對象非線性和滯后性問題，使主汽溫控制系統性能有了較大的提高。

1 主汽溫綜合控制

1.1 超臨界機組主汽溫基本控制策略及工藝流程

超臨界直流鍋爐主汽溫的控制由兩個調節系統實現。一是通過調節燃水比來維持汽水流程中某點的工質溫度，對主汽溫的進行粗調；二是通過設置二級過熱器噴水減溫裝置，對主汽溫的進行細調[2]。

超臨界機組主汽溫工藝流程圖如圖1所示。蒸汽經過了水冷壁，一級過熱器、屏式過熱器和末級過熱器等受熱面后形成主蒸汽。由于噴水減溫調節慣性小、響應快，A、B兩側同時設置兩級噴水減溫裝置，作為細調手段。

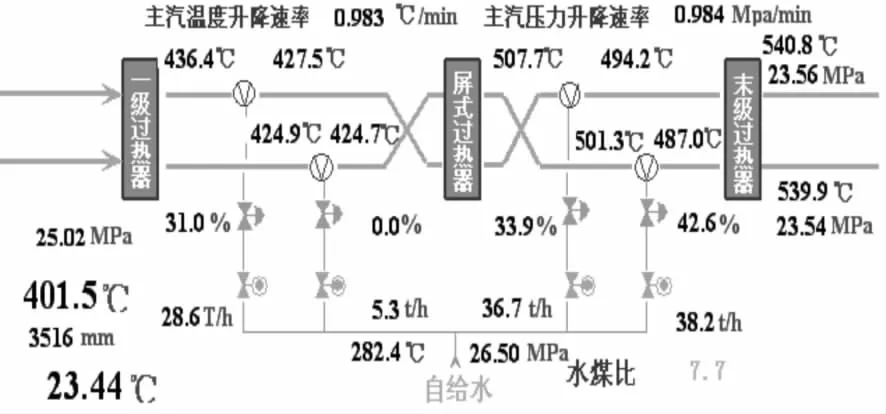
圖1 主汽溫工藝流程圖Fig.1 Main steam temperature process flow diagram

該超臨界機組噴水減溫原控制方案中一、二級減溫均采用了串級控制。但串級控制在調試整定過程中存在較大難度，且易造成較大偏差及積分飽和。因此本方案只采用了一個PID調節器，設計了改進型Smith預估器對主汽溫對象惰性區特性進行預估補償，并結合模糊控制理論對PID參數進行在線調整的主汽溫綜合控制方案。

1.2 主汽溫綜合控制

1.2.1 改進型Smith預估器的設計

本文設計的改進型Smith預估控制器，通過預估補償使主汽溫惰性區對象等效成一個比例環節，進而減小控制通道的遲延，改善控制品質[3]。

主汽溫惰性區特性預估補償原理如圖2所示。

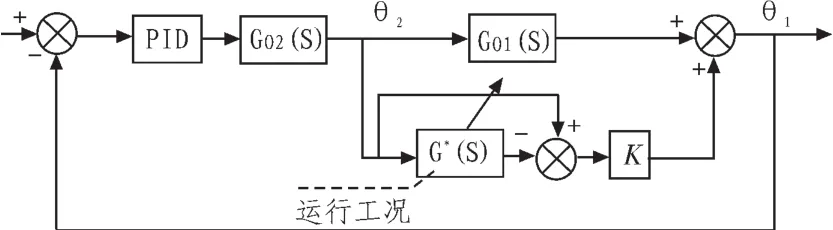
圖2 汽溫惰性區特性預估補償原理圖Fig.2 Schematic diagram of compensating the inert region character for the steam temperature

補償后的等效汽溫對象傳函為：

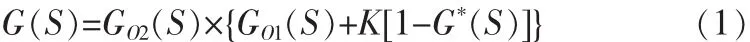
若要實現汽溫動態特性的近似完全補償，即KG*（S）≈GO1（S）時，則有：

其中θ1為過熱器出口蒸汽溫度；θ2為過熱器入口蒸汽溫度；GO1（S）為主汽溫惰性區對象特性；GO2（S）為主汽溫導前區對象特性；K為惰性區傳遞函數GO1（S）的放大系數；預估器模型 P（S）=K-GO1（S）。

其等效簡化框圖如圖3所示。

圖3 等效簡化原理圖Fig.3 Equivalent simplistic schematic diagram

由圖4可知經過預估補償后系統等效為一個單回路調節系統，其中導前區特性GO2（S）為一階慣性環節，等效汽溫對象為KGO2（S），控制通道遲延較小，這種調節方式將大大改善調節品質。

1.2.2 PID參數模糊調整

Smith預估控制能夠克服對象大遲延，但基于Smith預估器模型 P（S）=K-GO1（S），要想實現完全補償必須建立對象精確的數學模型，其補償效果對模型的誤差十分敏感，魯棒性差。而汽溫對象的導前區特性也隨運行工況而變化，因此其被控對象仍具有非線性和時變性。目前，模糊控制在工業控制中逐步得到應用，模糊控制的魯棒性和自適應能力較強，能夠很好的解決對象模型的不確定性、時變性和非線性問題，本文將模糊控制與PID控制相結合，通過自適應環節對PID控制器參數進行在線調整，實踐證明這種調整方法簡單易行，提高了控制器的自適應能力。基于改進型Smith預估器的模糊自適應PID控制系統原理示意圖如圖4所示。

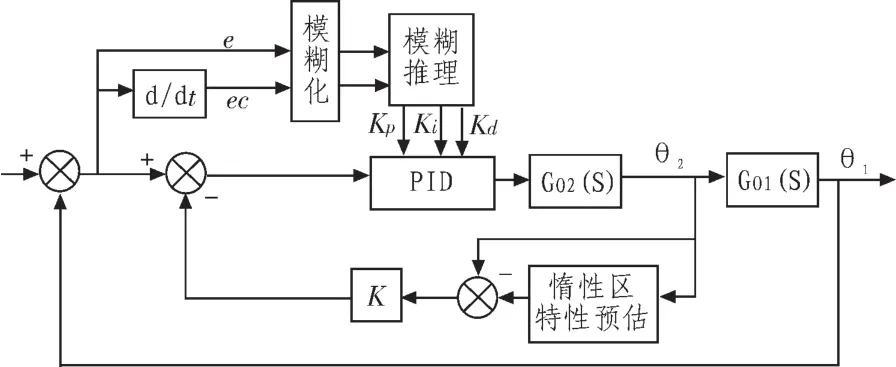
圖4 改進型Smith預估器的模糊自適應PID控制系統原理圖Fig.4 Schematic diagram of improved smith predictor fuzzy self-adaptive PID control system

2 汽溫控制方案仿真研究

2.1 模糊策略

2.1.1 模糊化

將系統誤差e和誤差變化率ec變化范圍定義為模糊集上的論域。根據實際情況，語言變量論域與語言值集合設為：

e=[-3，3]；{NB，NM，NS，ZO，PS，PM，PB}

ec=[-3，3]；{NB，NM，NS，ZO，PS，PM，PB}

輸出分別是：kp，ki，kd，語言變量論域與語言值集合設為：

kp=[-0.2，0.2]；{NB，NM，NS，ZO，PS，PM，PB}

ki=[-0.05，0.05]；{NB，NM，NS，ZO，PS，PM，PB}

kd=[-2， 2]；{NB，NM，NS，ZO，PS，PM，PB}

kp，ki，kd的初始值為：0.3，0，1.0。

根據過熱汽溫對象的特性，一般可以應用經驗歸納法建立 kp，ki，kd的模糊控制規則表[4]如表 1 所示。

2.1.2 模糊推理與反模糊化

根據系統的誤差及誤差變化率得到相應的語言賦值，3個修正參數Δkp、Δki、Δkd通過表1所示的模糊控制規則可以得到其模糊量，可以采用重心整定法[5]對 Δkp、Δki、Δkd反模糊化處理，得到其精確量。

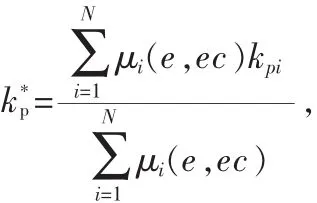
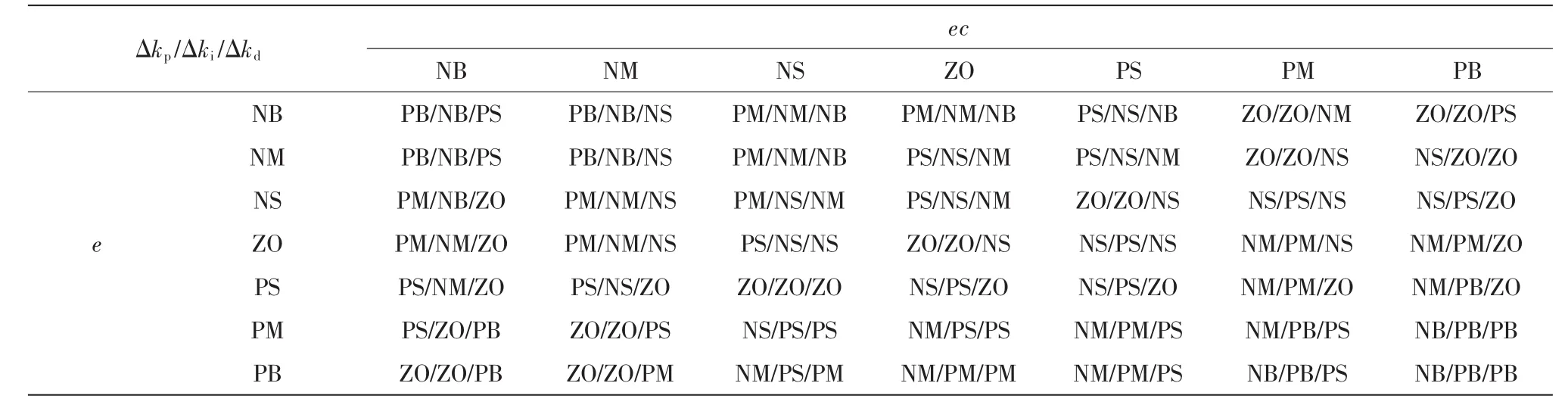
表 1 k p，k i，k d 的模糊規則表Tab.1 Fuzzy rule table of k p，k i，k d

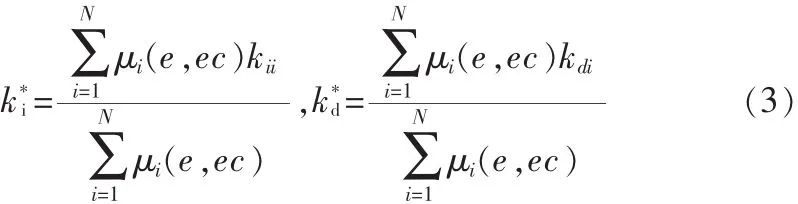
其中 kp、ki、kd為精確輸出量；kpi、kii、kdi為輸出變量；μ 為模糊集隸屬度函數；N為單點集數。應用模糊合成推理，根據各參數模糊控制模型及各模糊子集的隸屬度賦值表，得到控制器參數的模糊矩陣表，將求得的修正參數帶入下列公式計算，分別得到模糊自適應PID控制器的3個參數為：

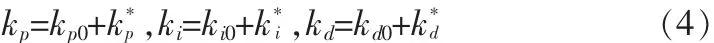
在線運行過程中，控制系統通過對模糊邏輯規則的處理、查表和運算，完成對PID參數的在線校正[6]。

2.2 仿真研究及結果分析

2.2.1 汽溫對象特性

通過減溫水階躍擾動試驗，測得超臨界機組主汽溫二級減溫器的進、出口溫度階躍響應曲線。根據響應曲線估算二級噴水減溫系統的惰性區及導前區傳遞函數為：

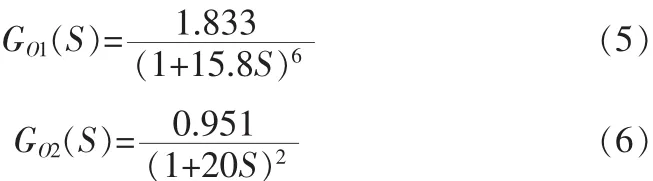
Smith預估器模型：

2.2.2 仿真研究及結果分析

根據汽溫對象動態特性，按圖2搭建系統仿真模型。為了觀察改進型Smith預估器模糊控制效果，同時還進行了常規PID和Smith預估器控制的仿真實驗，PID控制器參數kp=1.1、ki=0.017、kd=19.8，其仿真結果如圖5所示。對比3條仿真曲線，常規PID系統響應速度較快，過渡時間較長并有一定震蕩狀態出現；Smith預估控制的響應曲線在抑制超調，加快系統調節速度方面有較好的控制效果；模糊Smith控制效果最好，調節時間短且無超調及震蕩。

為觀察模糊Smith的抗干擾效果，系統在200s的時刻控制作用加入階躍擾動，仿真結果如圖6所示。仿真曲線表明，模糊Smith的抗干擾方面能力是最強的。擾動發生后，控制器參數在較短的時間內進行線調整，系統輸出平穩快速的恢復到平衡狀態。

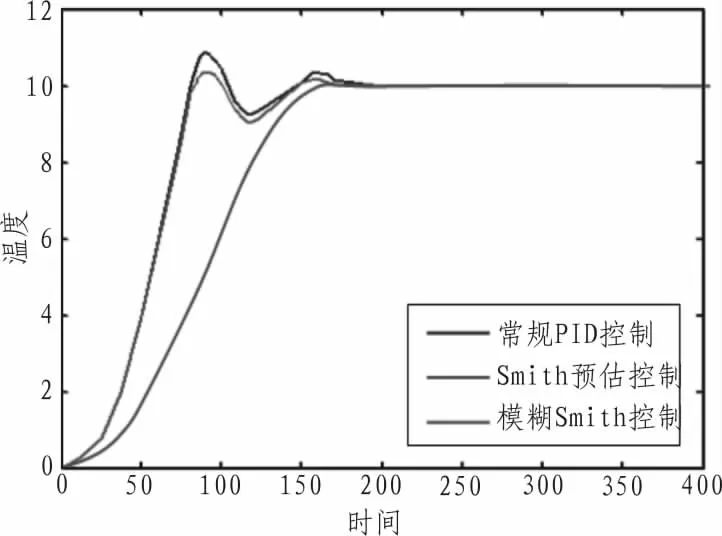
圖5 系統輸出響應曲線Fig.5 System output response curve

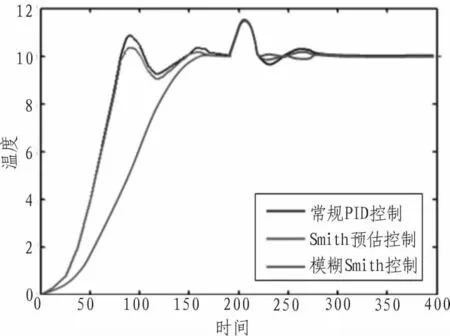
圖6 受到干擾后系統輸出響應曲線Fig.6 System output response curve after a disturbance

總之，通過系統仿真曲線分析，本文設計的改進型Smith預估器模糊控制器抗干擾能力強，有一定的容錯能力，這種汽溫綜合控制新方案能夠很好的克服主汽溫對象非線性和滯后性問題，具有良好的快速性、穩定性和魯棒性，使主汽溫控制系統性能有了較大的提高。

3 結束語

超臨界機組主汽溫對象較為復雜，存在較大遲延、時變性、非線性等特點，常規控制策略很難取得滿意的控制效果。本文提出了一種改進型Smith預估器對主汽溫對象惰性區特性進行預估補償，并將模糊控制理論與經典控制理論結合形成了主汽溫綜合控制方案。通過現場實際采集的歷史數據，對系統進行仿真實驗，結果表明該方案可以很好地解決主汽溫系統的非線性和滯后性問題。

[1]邊立秀.熱工控制系統[M].北京：中國電力出版社，2002.

[2]魏志，高東杰.超臨界直流鍋爐主汽溫控制[J].微計算機信息，2008（1）：17-18，61.WEIZhi，GAODong-jie.Thecontrol of main steamtemperature for supercritical once-through boilers[J].Microcomputer Information，2008（1）：17-18，61.

[3]張麗香，王琦.模擬量控制系統[M].北京：中國電力出版社，2006.

[4]劉金琨.先進PID控制及其MATLAB仿真[M].北京：電子工業出版社，2003.

[5]李平，嚴宇，肖智勇.Smith預估自適應模糊PID在溫控系統中的應用研究[J].電氣開關，2010（3）：39-42.LI Ping，YAN Yu，XIAO Zhi-yong.Application of smith predicted adaptive fuzzy PID control for the temperature control system[J].Electric Switchgear，2010（3）：39-42.

[6]李全俊，黃權，李錦.Smith預估模糊自適應 PID控制在時滯系統中的應用[J]，兵工自動化，2011（12）：49-52.LI Quan-jun，HUANG Quan，LI Jin.Application of smith predicted adaptive Fuzzy-PID controller in time-delay system[J].Ordnance Industry Automation，2011（12）：49-52.