利用數控機床換向特性分析的摩擦誤差補償方法

牟恩旭，馬振群，馮 斌，任建功

（西安交通大學機械工程學院，710049，西安）

摩擦是一種廣泛存在于機械動靜接觸面之間的自然現象［1］。當數控機床運行至換向處時，摩擦力矩方向突變所產生的非線性干擾會使控制系統產生較大的運動誤差［2］。為提高數控機床的運動精度，許多學者針對數控機床伺服進給系統摩擦誤差補償開展了研究工作。目前的補償方法可以分為基于摩擦模型的補償和基于前饋脈沖的補償。前者主要對伺服進給系統在運動過程中的摩擦力矩進行建模，并根據摩擦模型在電流環施加補償力矩實現補償。在摩擦模型的研究中比較著名的有Stribeck模型、Dahl模型及LuGre模型等［3-4］。上述模型從不同角度對動靜接觸面之間的摩擦特性進行了描述，但由于影響數控機床伺服進給系統摩擦特性的因素眾多，如溫度、接觸面潤滑情況、接觸面表面質量等因素的變化均會改變動靜接觸面間的摩擦特性［5］，仍難以獲得準確的摩擦模型。此外，由于大部分摩擦模型表達式復雜以及受到系統開放性的限制，電流環直接補償的方式在實際數控系統中難以實現，因此在工程應用中多采用基于前饋脈沖的補償方法。

基于前饋脈沖補償方法的補償原理為在伺服進給系統運動至換向位置時，在控制環路中加入補償脈沖，以抵消摩擦對運動的影響［6］。由于在控制器電流環施加補償脈沖易對伺服進給系統產生沖擊，且受到數控系統開放性限制，因此多將補償脈沖施加于位置環或速度環。目前，商用數控系統中主要依靠人工經驗調整補償脈沖參數，確定合理的補償參數較為困難。為實現摩擦誤差補償的自動化與智能化，Tung等提出通過重復控制器獲得補償脈沖參數的方法［7］，但因其需要改變控制器結構，具有在數控系統中可行性不強的缺點；陳光勝等提出了一種雙脈沖補償方法，并給出了補償脈沖參數計算方法［8］，但其為快速推動工作臺運動使用了矩形脈沖，具有易對工作臺產生沖擊的缺點；馮斌等通過對摩擦補償參數進行在線學習，獲得了摩擦補償脈沖參數［9］，但由于未能充分利用伺服進給系統換向處特性，存在尋優范圍大，學習時間長等不足。

本文對伺服進給系統換向處動態特性進行了分析，并根據補償脈沖對伺服進給系統運動狀態的影響，確定了合理補償脈沖參數的準則。基于該準則，提出了一種確定三角形摩擦誤差補償脈沖參數的方法，并在自主開發的開放式數控系統平臺上進行了摩擦誤差補償實驗。實驗結果表明，本文方法能夠有效地減小伺服進給系統換向處誤差，證明了本文方法的有效性及可行性。

1 換向處動態特性分析

為分析伺服進給系統換向處的動態特性，在搭建的開放式數控系統平臺上進行了相關實驗。該平臺由高性能伺服電機、驅動器及開放式數控系統組成，并采用高分辨力光柵尺進行全閉環運動控制，其機械部分為基于立式銑床改造的X-Y精密工作臺。該精密工作臺作為典型伺服進給系統，其在換向處的摩擦特性主要表現為在工作臺運動換向時，摩擦力矩方向發生突變［3］。圖1顯示了在未補償條件下，在開放式數控系統平臺上運行半徑為25mm、進給速度為1m／min的圓軌跡時，工作臺X軸位置誤差、實際速度及力矩電壓指令信號的變化情況。

由圖1可知，在到達換向時刻ta前，工作臺位置誤差、實際速度及力矩電壓指令處于正常狀態。在ta時刻后，工作臺實際速度為0，進入停駐狀態。此后，工作臺位置誤差開始逐漸增加，由于誤差的不斷累積，力矩電壓指令不斷增大。當力矩電壓指令所產生的力矩大于能使工作臺運動的分離力矩Tb時，工作臺開始運動，將此時的力矩電壓指令值稱為分離電壓Vb，將該時刻稱為分離時刻tb。當工作臺開始運動后，由于實際運動速度小于指令速度，位置誤差繼續增大，力矩電壓指令也隨之增大，工作臺加速運行。當到達tp時刻時，工作臺實際速度等于指令速度，此時位置誤差達到峰值。之后，伺服控制系統為減小位置誤差不斷進行調整，造成力矩電壓指令及實際速度出現波動，位置誤差逐漸減小。在時刻tc時，位置誤差值恢復至正常運行范圍，伺服控制系統完成對換向處摩擦影響的調整。

2 摩擦誤差補償原理及補償狀態分析

為確定合理補償脈沖參數，本節將結合運動控制模型，分析補償脈沖對工作臺動態特性造成的影響。

2.1 摩擦誤差補償原理

圖2為數控機床控制中常見的控制器結構，其采用三環PID控制方法，位置環為P控制器，速度環為PI控制器。其中位置環比例增益為Kpp，速度環比例增益為Kvp，速度環積分增益為Kvi，系統的電流環由于帶寬較高，可等效為比例環節，其比例系數為。考慮到速度環響應速度較位置環高，本文將補償脈沖施加于速度環處，即圖2中A位置。

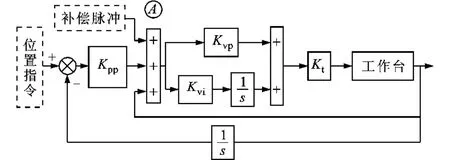
圖2 伺服進給系統控制器結構

相比于矩形脈沖，三角形補償脈沖能夠減小對系統的沖擊且補償效果更好，本文采用三角形補償脈沖對摩擦誤差進行補償。三角形補償脈沖示意圖如圖3所示，其中Pmax為脈沖峰值，t1與t2分別為補償時間參數1與補償時間參數2，圖中的橫軸起點為工作臺到達換向點時刻。為表述方便，在分析脈沖形態時以該時刻為零時刻點。

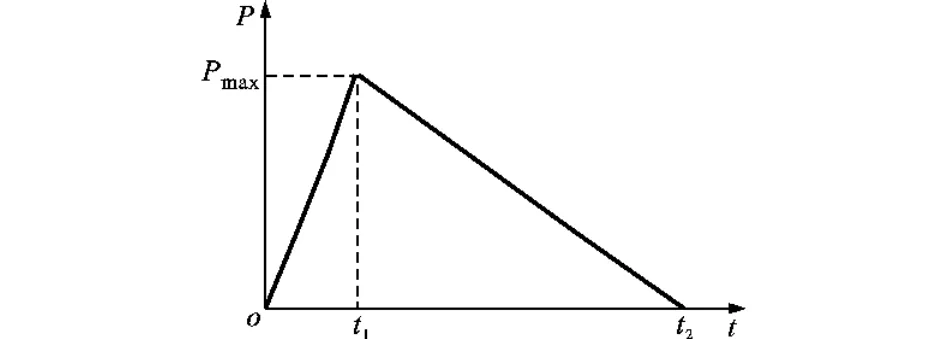
圖3 三角形補償脈沖形態示意圖

由圖3可知，三角形補償脈沖的形態函數fvc（t）表達式為

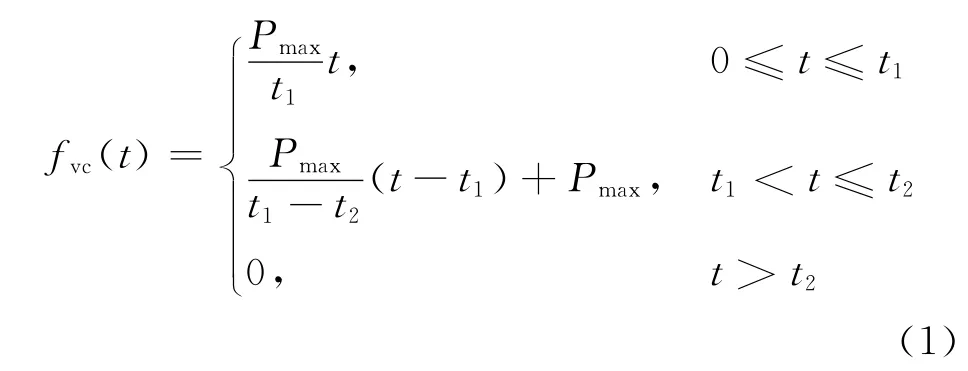
由速度環加入的補償脈沖，經速度控制器轉變為力矩電壓指令，其函數表達式為

對式（3）求導，可得

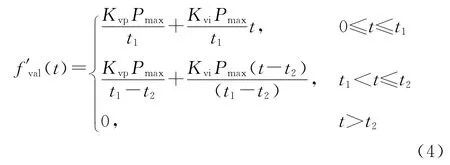
由式（4）可知，對于圖3中的三角形脈沖，由于Kvp、Kvi、Pmax、t1各項均為正值，fval（t）在t∈［0，t1）上單調遞增。當t∈（t1，t2］時，由于

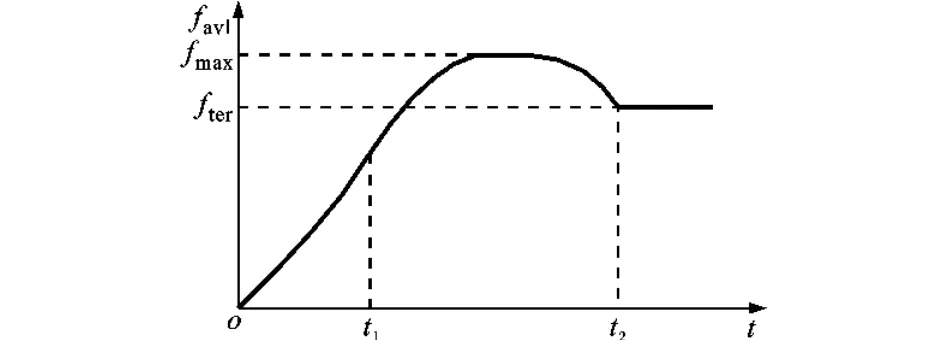
圖4 函數fval（t）的示意圖

通過以上分析可以發現，無論脈沖參數Pmax、t1和t2如何取值，其所產生的力矩指令電壓都會有一個先增后減的變化過程。下文將結合實驗說明不同參數下的補償脈沖對補償效果產生的影響。

2.2 不同參數補償脈沖作用下換向處特性分析

為便于分析及敘述，本文依據工作臺在換向處位置誤差形態，將工作臺在不同補償脈沖作用下的補償狀態分為3類。將補償后位置誤差絕對值在一較小范圍內的情況稱為理想補償。若位置誤差超出該范圍，且其尖峰方向同未補償時方向相同，則稱為欠補償。在欠補償狀態下，若位置誤差出現兩個尖峰，本文稱其為欠補償A狀態，而對于位置誤差只有一個尖峰的情況，則稱之為欠補償B狀態，如圖5a所示。若位置誤差超出該范圍，但其尖峰方向與未補償時相反，則稱為過補償。在過補償條件下，同樣會出現位置誤差呈現雙尖峰的情況，與欠補償A狀態下不同，此時兩個位置誤差尖峰的方向相反。本文將過補償狀態下位置誤差出現兩個尖峰的情況定義為過補償A狀態，而將過補償狀態下位置誤差只有一個尖峰的情況定義為過補償B狀態，如圖5b所示。

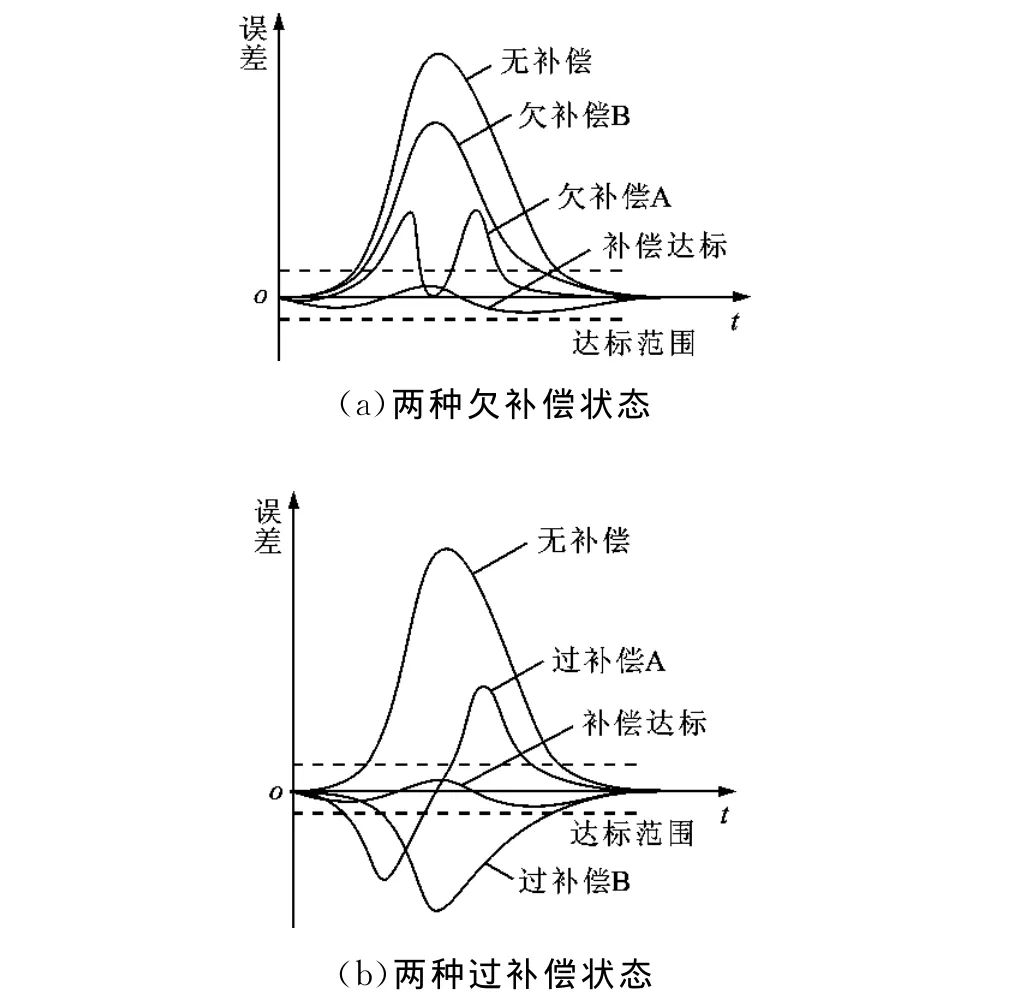
圖5 補償狀態示意圖

本文采集了工作臺X軸在進給速度為1m／min、半徑為25mm時，換向處的位置誤差、實際速度及力矩電壓指令信息。通過對以上信息進行對比，分析了不同參數補償脈沖作用下工作臺在換向處的動態特性。

通過觀察圖6可知，在理想補償狀態下，工作臺位置誤差無尖峰存在，力矩電壓指令以較快的速度上升，然后趨于平緩，工作臺實際速度均勻增加。這說明在補償脈沖的作用下，工作臺處于停駐狀態的時間較短，且速度上升平穩。

圖6同時顯示了工作臺的兩種欠補償狀態。從圖6a可以看出，在欠補償A狀態下，工作臺位置誤差出現兩個尖峰。綜合圖6b的實際速度信號可以發現，在此狀態下，由于補償脈沖的作用，工作臺在到達換向點后很快脫離了停駐狀態。當在脫離停駐狀態一段時間后，其實際速度再次為0，工作臺再次進入停駐狀態。通過觀察圖6c的力矩電壓指令信號可以發現，由于補償脈沖參數設置不合理，補償脈沖產生的力矩電壓指令在上升后，出現了較為明顯的下降。當力矩電壓指令所產生的力矩小于摩擦力矩時，工作臺再次發生停駐。此后，由于誤差的累積，力矩電壓指令再次增大，工作臺在經歷了一段時間的停駐后再次開始運動。在此過程中，工作臺經歷了停駐-運動-停駐-運動的過程，造成了位置誤差曲線中的兩個誤差尖峰。

在欠補償B狀態下，通過觀察實際速度曲線可以發現，同無補償狀態一樣，工作臺經歷了停駐-運動的過程。但是，在補償脈沖作用下，力矩電壓指令變化較無補償狀態下快，而較理想補償狀態下慢，因此其對換向誤差的補償作用不及使工作臺處于理想補償狀態下的補償脈沖。相比于欠補償A狀態，力矩電壓指令下降不明顯，其所產生的力矩能夠維持工作臺持續運動，未使工作臺出現再次進入停駐狀態的情況。

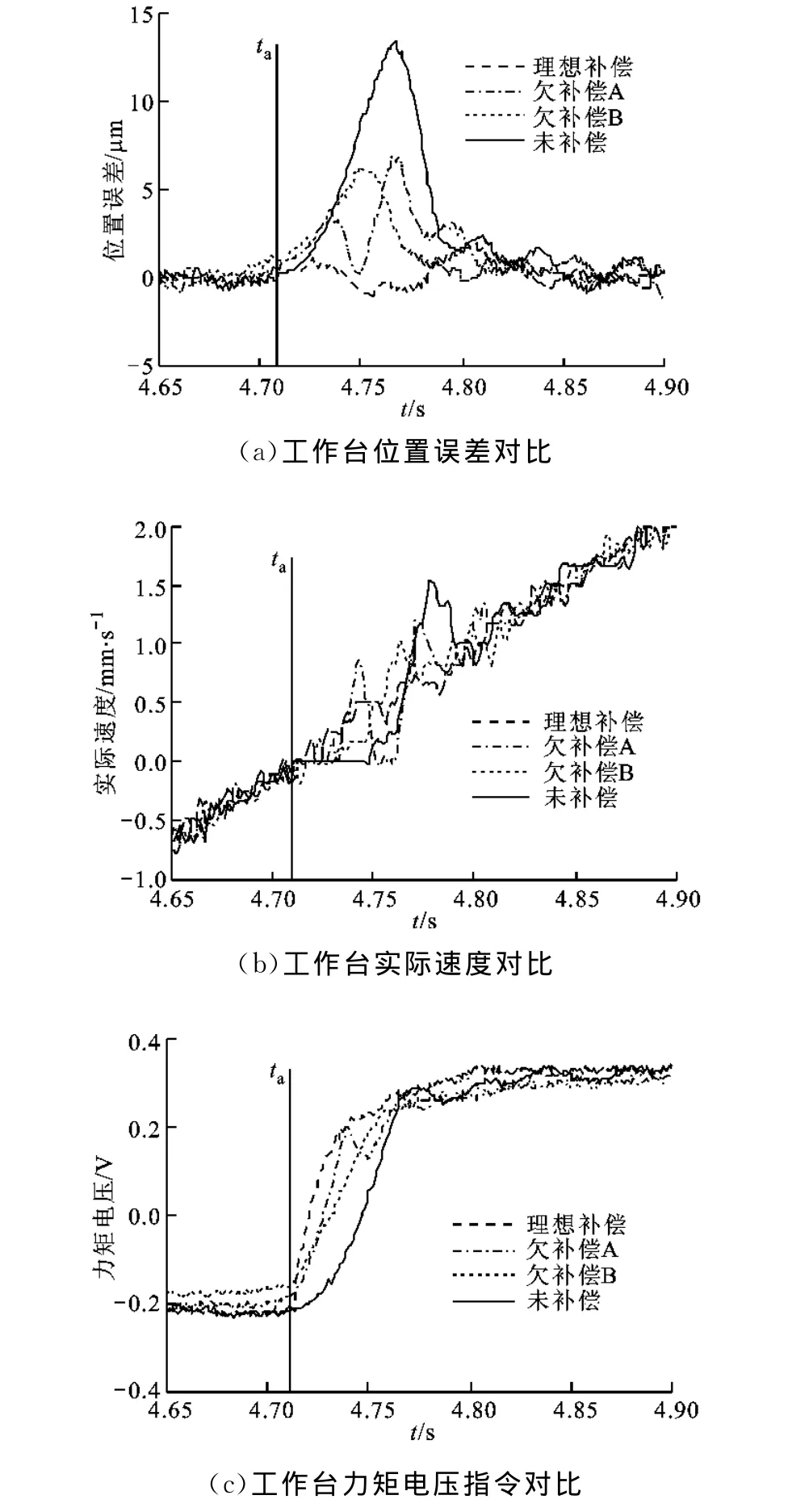
圖6 欠補償狀態下工作臺運動信息對比

圖7 顯示了工作臺在過補償A狀態下的動態特性。通過觀察其實際速度曲線可以發現，工作臺如在欠補償A狀態下一樣經歷了停駐-運動-停駐-運動的過程，其原因與前述相同，這里不再贅述。同樣，對于過補償B狀態，工作臺如在欠補償B狀態下一樣經歷了停駐-運動的過程。但是，由于在過補償狀態下，補償脈沖幅值大且變化快，引起力矩電壓指令在開始階段急劇增大，使實際運動速度大于指令速度，從而形成了與欠補償情況下方向相反的位置誤差，產生了所謂的“過切”現象。過切現象會導致所加工工件產生無法彌補的后果，且會使刀具加速磨損乃至直接損壞［11］，因此在實際補償中應盡量避免發生過補償現象。

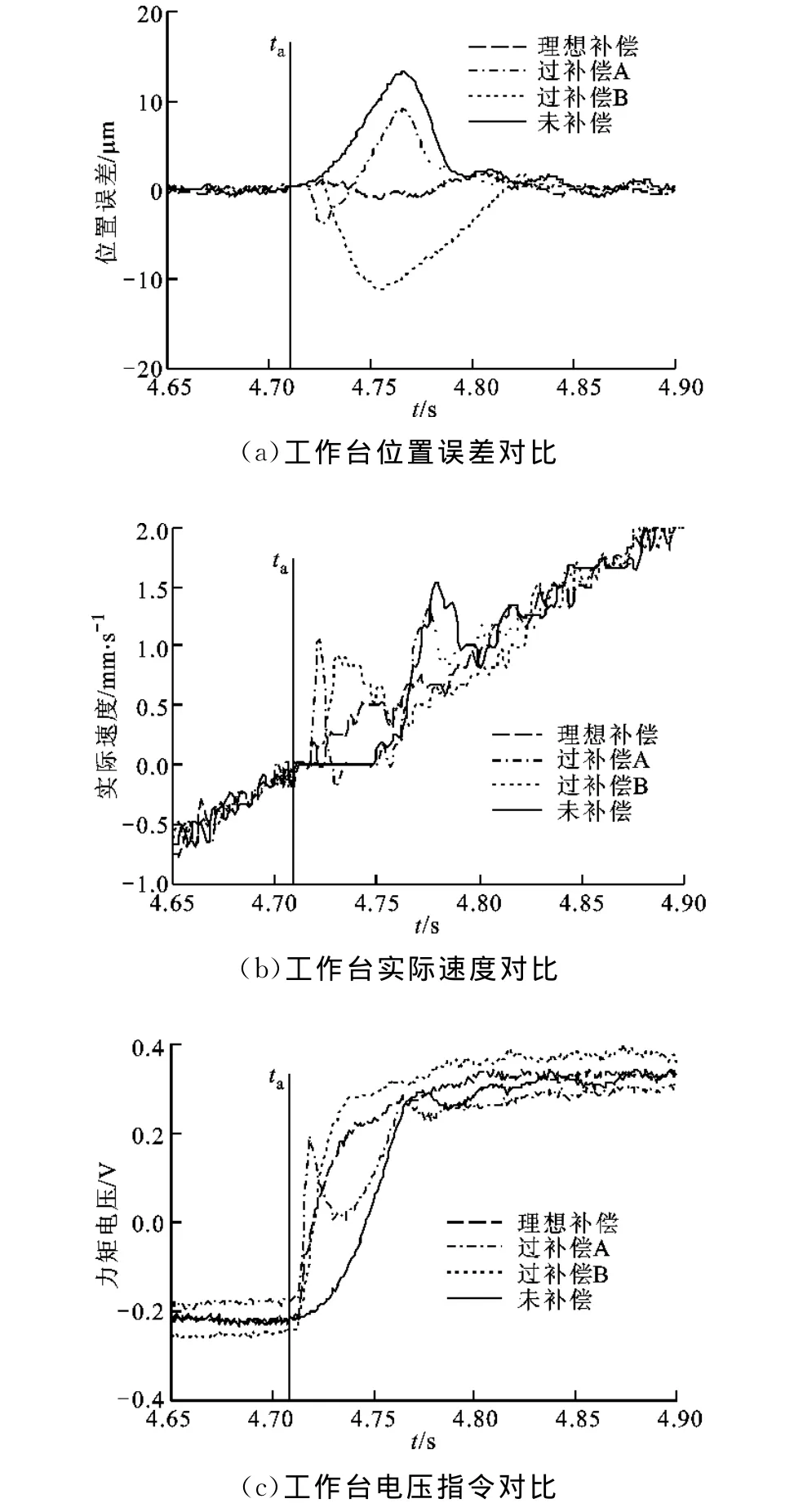
圖7 過補償狀態下工作臺運動信息對比

3 三角形補償脈沖參數的確定

3.1 合理補償脈沖參數

（1）在補償開始階段，補償脈沖應使力矩電壓指令以適當的速率上升并達到分離電壓Vb，從而使工作臺脫離停駐狀態，即

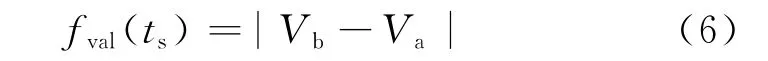
式中：Va為換向點處力矩電壓指令值；ts為加入補償脈沖后的分離時刻。

（2）在補償結束的t2時刻，補償脈沖所產生力矩電壓指令終值fval（t2）應使工作臺的驅動力矩至少等于其阻力矩，以保證工作臺不會再次進入停駐狀態。同時，為了不使t2時刻實際運動速度超過速度指令，令t2時刻工作臺力矩電壓指令等于無補償時系統調整結束tc時刻的力矩電壓指令Vc，即

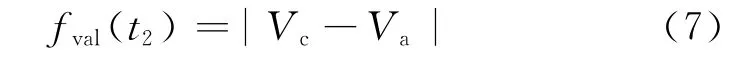
3.2 合理補償脈沖參數計算方法

在數控系統中，計算合理補償脈沖參數所需信息，可通過以下方法獲取。

（1）在未補償條件下，使工作臺以特定軌跡運行，獲得工作臺在無補償條件下換向處的位置反饋曲線、位置誤差曲線及力矩電壓指令曲線。對位置反饋曲線進行差分及平滑處理，獲得實際速度曲線。通過實際速度曲線確定換向時刻ta、未補償時分離時刻tb，通過位置誤差曲線確定調整完成時刻tc。在力矩電壓指令曲線上讀出ta、tb、tc時刻對應的力矩電壓指令Va、Vb、Vc。

（2）為使工作臺能較快脫離停駐狀態，將ts取值為

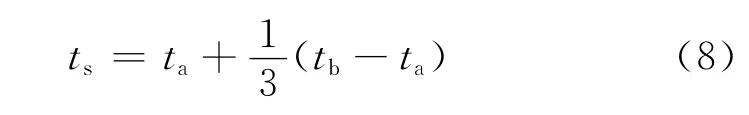
（3）根據上文所總結的合理補償脈沖參數來確定準則，聯立式（3）、式（6）與式（7），可得

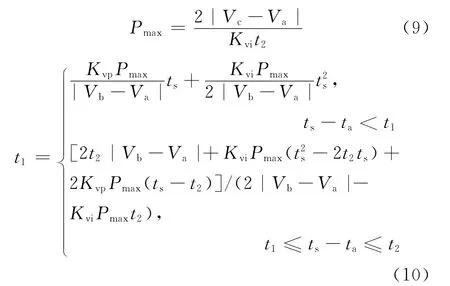
為使補償脈沖所產生力矩電壓指令盡量平緩，避免引起系統振蕩，應使t2的取值盡量大，這里根據無補償情況下的穩定時間確定t2

由于在實際中，工作臺在各位置的摩擦特性不盡相同，因此在一處獲得的合理補償脈沖參數未必能適用于全行程。為避免在個別位置出現過補償現象，實際中應選用的補償參數可根據補償效果進行調整，可將實際選用的補償脈沖峰值定為

式中：δ為調整系數，取值為［0.8，1］。

4 驗證實驗

為驗證本文所提出方法的有效性，在開發的開放式數控系統平臺上進行摩擦誤差補償實驗。

控制精密工作臺X軸先后以進給速度F為1m／min和3m／min、運行幅值為25cm的正弦軌跡，根據上文介紹方法采集所需要的相關參數。在一個運動周期中，工作臺經歷兩個換向點，這里將力矩電壓信號由負變為正的方向記為C向，反之記為D向。由于機械結構存在裝配水平度差等缺陷，C向與D向的摩擦特性存在較明顯的差異。為了方便記述，將ta時刻記為0，各參數實測值如表1所示。

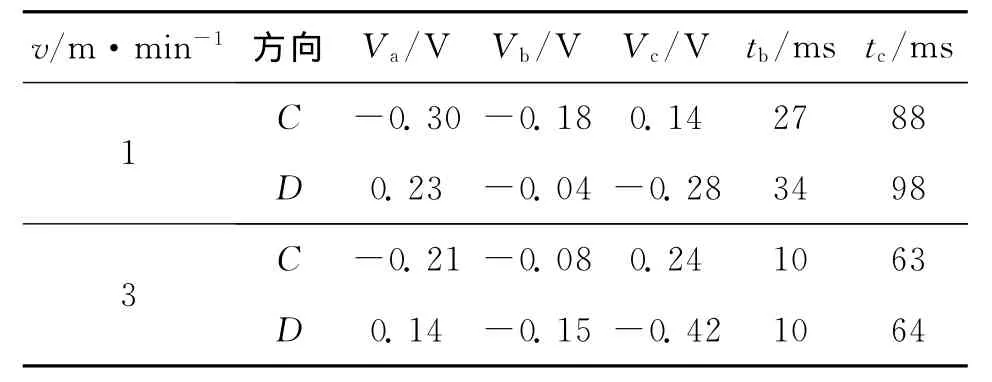
表1 無補償狀態下實測參數值

實際控制器Kvp為0.06，Kvi為5，取δ為1。將表1中的數據代入式（8）～式（12），計算得到在不同速度下補償脈沖所應選取的參數，見表2。

表2 摩擦誤差補償脈沖參數計算值

將設置好的補償脈沖施加至圖2所示A位置，在1m／min和3m／min進給速度下驗證補償效果，實驗結果如圖8所示。為了對實驗結果進行量化分析，對從換向時刻開始的監測時間tM內的跟隨誤差進行監測，并采用絕對誤差尖峰及絕對誤差平均值對補償效果進行綜合評價。tM值根據各工況換向過程所需的時間進行設定，這里tM取為150ms。表3中列出了不同進給速度下補償前后監測時間tM內絕對誤差最大值P及其平均值M 的數值。綜合圖8及表3可以發現，本文方法在不同工況下均能有效減小工作臺換向處誤差，獲得較理想的補償效果。

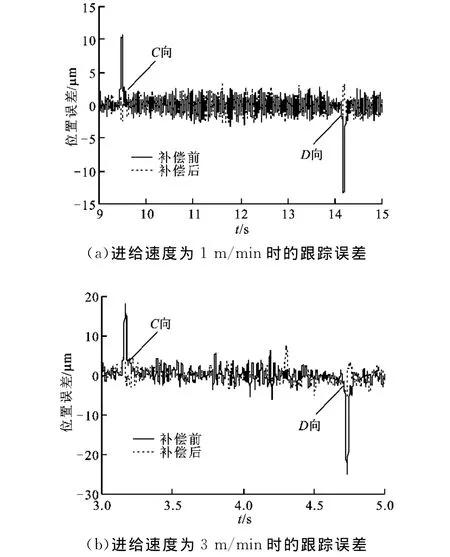
圖8 摩擦誤差補償效果對比

表3 摩擦誤差補償效果綜合評價表

5 結 論

（1）針對工業實際中難以確定數控機床摩擦誤差補償脈沖參數的問題，本文提出了一種基于數控機床換向特性分析的摩擦誤差補償方法。該方法通過獲得工作臺在無補償狀態下的相關信息，根據所提出的合理脈沖參數確定準則及計算公式對三角形補償脈沖的參數進行計算。由于充分利用了伺服進給系統換向處的特性，實現了對補償脈沖參數的直接計算，大幅提高了調試效率。

（2）分析了伺服進給系統在換向處的動態特性。結合實際補償實驗數據及對補償脈沖形態的推導，分析了補償脈沖對工作臺換向處動態特性的影響。根據分析結果，總結了合理補償脈沖參數以確定準則。

（3）在X-Y精密工作臺的X軸上以不同進給速度進行了摩擦誤差補償實驗。實驗結果表明，該方法在不同工況下均能有效減小換向處絕對誤差尖峰值及絕對誤差均值，其對換向處誤差尖峰值的抑制達到70%以上，對換向處誤差平均值的抑制達到50%以上，驗證了該方法的可行性及有效性。

［1］ OLSSON H，?STR?M K J，DE WIT C C， et al.Friction models and friction compensation ［J］.European Journal of Control，1998，4（3）：176-195.

［2］ EUN-CHAN P，HYUK L，CHONG-HO C.Position control of X-Y table at velocity reversal using presliding friction characteristics ［J］.IEEE Transactions on Control Systems Technology，2003，11（1）：24-31.

［3］ ARMSTRONG-HéLOUVRY B， DUPONT P，DE WIT C C.A survey of models，analysis tools and compensation methods for the control of machines with friction［J］.Automatica，1994，30（7）：1083-1138.

［4］ SYH-SHIUH Y，HSIN-CHUN S.Development of friction identification methods for feed drives of CNC machine tools［J］.International Journal of Advanced Manufacturing Technology，2011，52（1／2／3／4）：263-278.

［5］ HSIEH C，PAN Y C.Dynamic behavior and modelling of the pre-sliding static friction［J］.Wear，2000，242（1／2）：1-17.

［6］ MEI X S，TSUTSUMI M，TAO T，et al.Study on the compensation of error by stick-slip for highprecision table ［J］.International Journal of Machine Tools ＆ Manufacture，2004，44（5）：503-510.

［7］ TUNG E D，ANWAR G，TOMIZUKA M.Low-velocity friction compensation and feedforward solution based on repetitive control［J］.ASME Journal of Dynamic Systems Measurement and Control，1993，115（2A）：279-284.

［8］ 陳光勝，梅雪松，陶濤.X-Y工作臺摩擦誤差補償方法的研究 ［J］.西安交通大學學報，2011，45（1）：69-73.

CHEN Guangsheng，MEI Xuesong，TAO Tao.Compensation of friction error for X-Ytable［J］.Journal of Xi’an Jiaotong University，2011，45（1）：69-73.

［9］ 馮斌，梅雪松，楊軍，等.數控機床摩擦誤差自適應補償方法研究 ［J］.西安交通大學學報，2013，47（11）：65-69.

FENG Bin， MEI Xuesong， YANG Jun，et al.Adaptive compensation of friction error for numerical control machine tool［J］.Journal of Xi’an Jiaotong University，2013，47（11）：65-69.

［10］KIM M S，CHUNG S C.Integrated design methodology of ball-screw driven servomechanisms with discrete controllers：part I modelling and performance analysis［J］.Mechatronics，2006，16（8）：491-502.

［11］ELLIS G.Control system design guide［M］.San Diego，USA：Elsevier Academic Press，2004：51-52.

［本刊相關文獻鏈接］

馮斌，梅雪松，楊軍，等.數控機床摩擦誤差自適應補償方法研究.2013，47（11）：65-69.［doi：10.7652／xjtuxb201311012］

李學偉，趙萬華，盧秉恒.軌跡誤差建模的多軸聯動機床輪廓誤 差 補 償 技 術.2012，46（3）：47-52.［doi：10.7652／xjtuxb 201203009］

馬曉龍，陳貴燦.固定位寬乘法器的量化誤差補償方法及電路實 現.2011，45（12）：75-81.［doi：10.7652／xjtuxb201112 014］

陳光勝，梅雪松，陶濤.X-Y工作臺摩擦誤差補償方法的研究.2011，45（1）：69-73.［doi：10.7652／xjtuxb201101014］

周玉清，陶濤，梅雪松，等.旋轉軸與平移軸聯動誤差的快速測量及溯源.2010，44（5）：80-84.［doi：10.7652／xjtuxb201005 017］

李彪，劉新正，李黎川.具有低通濾波的改進電壓型磁鏈觀測器.2009，43（12）：91-95.［doi：10.7652／xjtuxb200912019］

韋進文，郭俊杰.坐標測量機動力學剛度估計與加速度誤差補償.2009，43（1）：47-51.［doi：10.7652／xjtuxb200901011］

丁建軍，蔣莊德，李兵，等.線結構光掃描測頭誤差分析與補償方法.2008，42（3）：286-290.［doi：10.7652／xjtuxb200803 007］

劉保華，李兵，崔希君，等.一種多線結構光測頭的誤差補償方法.2007，41（1）：50-54.［doi：10.7652／xjtuxb200701012］