雙晶壓電懸臂梁電荷輸出特性實驗研究
劉 陽,羅 奇,孫 科,陶孟倫,陳定方
(武漢理工大學智能制造與控制研究所,湖北 武漢430063)
壓電陶瓷是一種能夠將機械能與電能相互轉換的功能陶瓷材料,具有制作成本和難度低、換能效率高[1]等優點。目前的壓電能量收集器在頻率匹配、裝置結構等技術方面并未完全成熟,本文通過理論建模與仿真分析,設計一種基于PZT-5H壓電陶瓷材料的并聯式雙晶壓電懸臂梁,探討該結構下的電荷輸出特性,同時結合實驗總結其規律。
1 壓電懸臂梁結構及工作原理
壓電效應分為逆壓電效應與正壓電效應。前者是壓電片在外電場作用下產生形變,將電能轉化為機械能,人們也正是利用這種原理,開發制造出精密電動機、壓電泵、超聲波電機[2]等裝置;后者則是壓電材料在外力作用下產生電荷,將機械能轉化為電能,本文就是利用正壓電效應,研究壓電懸臂梁的輸出特性。并聯式雙晶壓電懸臂梁(圖1)主要由鈹青銅金屬懸臂梁、PZT-5H壓電陶瓷片和支座組成,上下端壓電片在粘貼時保證極化方向相同,電路連接時將上下2層壓電陶瓷片連接為正極,將電極板作為負極。同時,金屬片兩端延伸出一部分電極,其中一端與基座固定,另一端隨著環境自由振動。
環境中的外部振動激勵,會導致懸臂梁受迫振動,發生彎曲變形,進而引起壓電陶瓷片內應力與內應變的改變。根據相關的壓電理論,壓電陶瓷片內部產生應力應變時,其表面將會有自由電荷生成。在這種情況下,壓電振子產生彎曲變形,壓電懸臂梁的上、下層電極之間會產生一種隨外界激勵變化而變化的電勢差,為負載供電。當環境中的激勵頻率與懸臂梁的固有頻率一致時,將會引起懸臂梁共振,壓電陶瓷片的應力與應變在此刻變化達到最大,從而使壓電懸臂梁輸出的電壓變化達到最大。
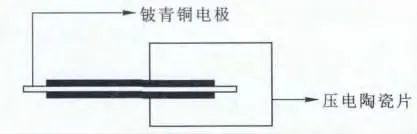
圖1 并聯式雙晶壓電懸臂梁結構
2 雙晶壓電懸臂梁的有限元仿真分析
利用ANSYS軟件進行并聯式雙晶壓電懸臂梁的仿真分析是一種結構-電場耦合分析。壓電分析考慮到了結構與電場的相互作用,求解由于所施加位移造成的電壓分布。
Solid5單元具有三維磁場、熱場、電場、壓電場和結構場分析能力,并能在各場之間實現有限元的耦合。這里將Solid5單元用于壓電材料的建模。Circu94是一個具有壓電自由度及正或負電荷貫通變量的電路單元,通過KEYOPT選擇,可作為一個線性電阻器、電容器、感應器或一個獨立的電壓/電流源。這里,Circu94可以與Solid5一起使用,以模擬電路耦合電壓分析。支撐層鈹青銅片與45鋼質量塊則采用Solid45單元。不考慮粘接層的影響,并設定支撐層與壓電層的位移具有一致性。根據圖1及壓電懸臂梁相關參數(表1),建立ANSYS模型,進行模態分析求解后得到4階模態結果:一階頻率f1=21.705Hz,二階頻率f2=106.62Hz,三階頻率f3=290.03Hz,四階頻率f4=659.71Hz。再進行諧響應分析。頻率范圍0~1 000Hz,設置0.02的阻尼,走100步,分析完后處理得到的結果如圖2所示。

表1 壓電懸臂梁相關參數

圖2 壓電懸臂梁諧響應分析
觀察可知,輸出電壓在固有頻率附近最大,且一階固有頻率影響最大。為了壓電能量收集器的采集效率最大化,應使懸臂梁固有頻率盡可能接近外界振動頻率。接下來著重分析一階固有頻率附近的輸出特性,縮減頻率范圍至0~100Hz,以提高結果準確性。
懸臂梁末段無質量塊時的頻率特性如圖3所示,可見54Hz時達到最大輸出電壓2.7V。

圖3 無質量塊時頻率特性
懸臂梁末段附有一塊質量塊時的頻率特性如圖4所示,可見22Hz時達到最大輸出電壓11.5V。
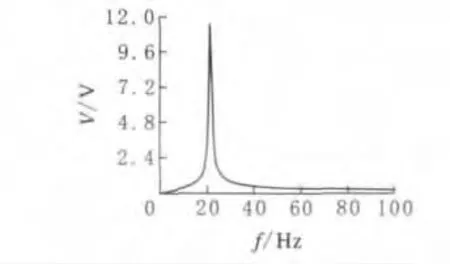
圖4 單質量塊壓電懸臂梁頻率特性
比較分析可知,質量塊的添加能顯著降低懸臂梁結構的固有頻率,并提高輸出電壓值。
3 并聯式雙晶壓電懸臂梁實驗
選用的是PZT-5H壓電陶瓷片,利用導電膠,將制作的并聯式雙晶壓電陶瓷片與基座絕緣固定后,安裝在HEV-2激振器上,使得壓電片能與激振器保持同頻率的振動。采用GW GFG-8016G信號發生器,將其輸出端接入功率放大器,然后連接激振器。這個過程使信號發生器輸入的標準正弦波經GF2210功率放大器一定程度放大后,讓激振器振動。同時,將功率放大器放大后的激勵電壓接入HITAC V-212數字示波器CH1端口,利用示波器測出懸臂梁在一定振動激勵下的輸出電壓(圖5)。

圖5 雙晶壓電懸臂梁實驗裝置圖
信號發生器產生正弦信號,經功率放大器放大后驅動激振器,帶動激振器上的壓電懸臂梁振動,電壓信號經過示波器輸出(圖6)。

圖6 輸出電壓波形
從圖6波形可知,壓電懸臂梁在正弦激勵的情況下,電壓輸出也為正弦,并且整體表現穩定,由此可得壓電懸臂梁作為電源是可行的。
4 實驗結果分析
通過固定信號發生器的正弦信號峰值電壓和功率放大器的放大電壓,改變激振頻率,測量無質量塊壓電懸臂梁的電壓輸出頻率特性,其結果見圖7。由圖7可知,在53Hz時,懸臂梁輸出電壓達到最大,為3V,且電壓在固有頻率附近變化顯著,表明壓電材料的輸出電壓隨著振幅的增大而增大,然而,在30Hz與70Hz附近仍有2處波峰突起,經對比分析,此是壓電片本身夾持部分的干擾所致。于是,保持相同的激振電壓與放大電壓的情況下,在懸臂梁的自由端粘接上一定數量質量為15g的質量塊,再分別測出它們的頻率特性(圖8)。
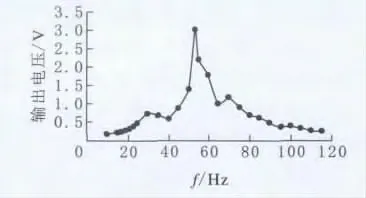
圖7 無質量塊壓電懸臂梁頻率特性
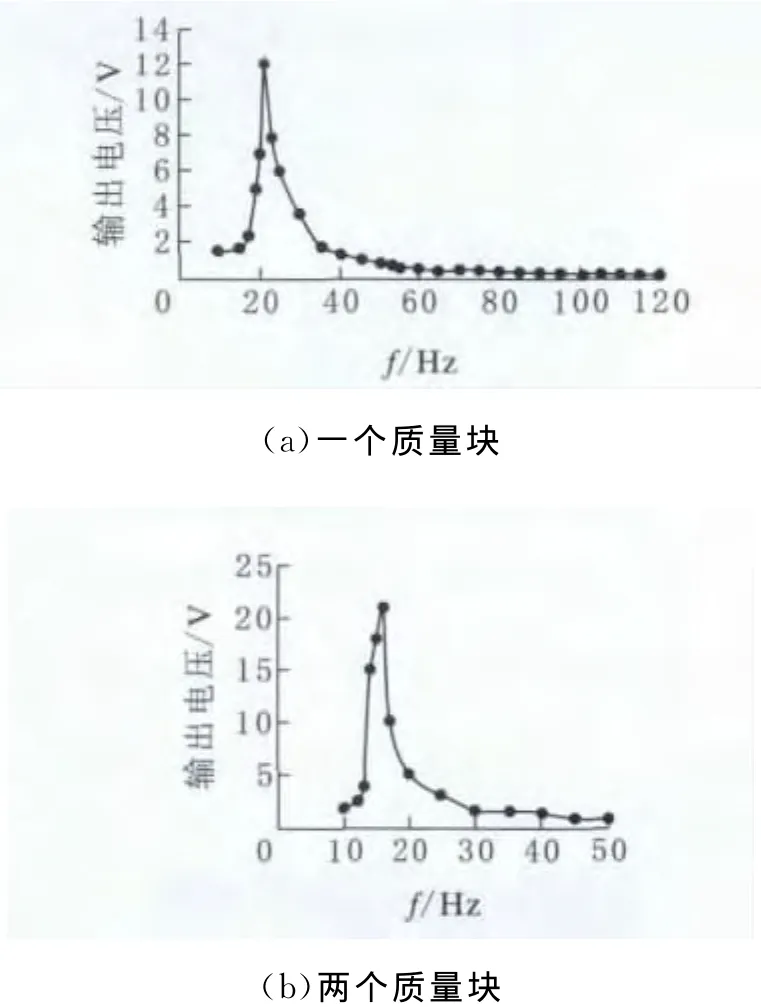
圖8 不同質量塊雙晶懸臂梁頻率特性
經過調整,頻率曲線完全符合理論規律:末端一個質量塊情況下,壓電懸臂梁輸出電壓在21Hz時達到12V峰值;末段有兩個質量塊情況下,壓電懸臂梁輸出電壓在16Hz時達到21V峰值。圖9是三次實驗的雙晶壓電懸臂梁頻率特性圖。
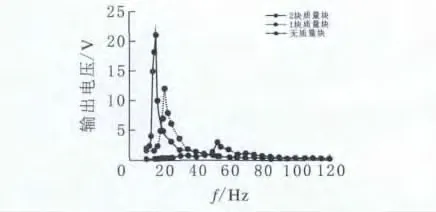
圖9 三次實驗的雙晶壓電懸臂梁頻率特性
由此可得出結論:在外界激勵相同的情況下,雙晶壓電懸臂梁在共振頻率附近輸出電壓最大,變化最大。末段質量塊會降低懸臂梁的固有頻率,同時增加同等激勵下的振幅,從而增大懸臂梁的輸出電壓。此后,在電路中接入了1 000Ω的電阻,測量其功率曲線(圖10)。

圖10 雙晶壓電懸臂梁功率特性
由測量結果可得出以下結論:壓電懸臂梁的功率曲線整體與頻率特性曲線規律吻合,在共振頻率附近呈現峰值變化,最大輸出功率約為0.126mW。
壓電懸臂梁在一定環境條件下作為能量收集器的可行性雖得到驗證,但其弊端也很明顯,后續實驗將嘗試把多片不同固有頻率的壓電片連接在一起,人為制造出一組寬頻、高電量輸出的壓電懸臂梁陣列。
[1] Kwon D W,Gabriel A R.a 2-um BICMOS rectionfierfree AC-DC piezoelectric energy harvester-charger IC[J].IEEE Transacations on Biomedical Circuits and Systems,2010,4(06):400-409.
[2] 曾 平,溫建明.新型慣性式壓電驅動機構的研究[J].光學精密工程,2006,14(04):623-627.
[3] 袁秋潔.基于壓電材料的振動能量收集理論及其結構分析[D].北京:華北電力大學,2010.
[4] 黨沙沙,許 洋,張紅松.ANSYS12.0多物理耦合場有限元分析從入門到精通[M].北京:機械工業出版社,2010.

