Ⅰ型軌道板端離縫對軌道結構及車輛動力特性的影響

楊俊斌， 劉學毅， 劉永孝， 代 豐

(西南交通大學高速鐵路線路工程教育部重點實驗室，四川 成都610031)

Ⅰ型板式軌道的軌道板與CA (cement asphalt)砂漿層之間的離縫現象是軌道結構常見的動態不平順之一. 在高速列車荷載作用下，沒有離縫現象時，軌道板是全支承受力狀態;若存在離縫現象，軌道板的受力狀態會變為兩種情況:一種情況是無列車荷載時離縫區軌道板與CA 砂漿不接觸，當有列車荷載作用時，離縫區軌道板與CA 砂漿接觸;另一種情況是無論有無列車荷載作用，離縫區軌道板與CA 砂漿層均不再接觸，第二種情況的離縫又被稱為脫空.

目前，關于離縫現象對軌道結構以及車輛動力特性影響的研究還較少.文獻［1］計算分析了Ⅰ型軌道板中部有離縫時軌道結構的各項力學指標，但計算模型中將高速列車荷載簡化為一個激振力，且未考慮軌道幾何不平順對計算結果的影響. 文獻［2］通過將實測溫度梯度與數值模擬相結合，確定了Ⅱ型軌道早期層間離縫產生的原因，未對離縫對Ⅱ型軌道結構力學性能的影響進行分析. 文獻［3］在分析溫度荷載及自重作用下離縫長度的變化對Ⅱ型軌道結構力學性能的影響時，未考慮列車荷載的影響.

本文以Ⅰ型板式軌道常見的軌道板端部離縫(圖1)為研究對象，采用車輛-軌道垂向耦合動力學理論，分析了高速列車荷載作用下，不同離縫高度及長度對軌道及車輛動力特性的影響.本文的研究可為更深入地了解這一現象對軌道結構以及列車的不良影響提供一定的參考.

圖1 軌道板端離縫示意Fig.1 Sketch of seam at the end of slab

1 車輛-軌道垂向耦合動力學理論

1.1 車輛-Ⅰ型板式軌道垂向耦合動力學模型

在車輛-Ⅰ型板式軌道耦合動力學模型中，車輛系統的車體、構架及輪對用實體單元進行模擬，并賦予剛體屬性. 車體和轉向架構架分別考慮沉浮、點頭和側滾3 個自由度. 輪對在考慮輪軌之間的耦合振動相對位移后，還要加上沉浮及側滾共8 個自由度，因此，車輛系統共計17 個自由度［4-5］.車輛系統中的一系和二系懸掛，采用離散的垂向梁單元進行模擬［6］.

Ⅰ型板式軌道中的鋼軌用連續彈性點支承基礎上的Euler 梁模擬，軌道板用彈性地基上的等厚度矩形薄板模擬.扣件系統主要起彈性支承與減振作用，CA 砂漿具有半剛性半彈性特征，土質路基也具有一定的彈性，因此，在模型中，扣件、CA 砂漿和土質路基均作為垂向彈簧-阻尼系統，采用離散的垂向梁單元模擬［7-9］. 離縫區CA 砂漿采用非線性彈簧單元模擬. 圖2 為離縫高度為2.5 mm 時，離縫區非線性彈簧的力-位移曲線.

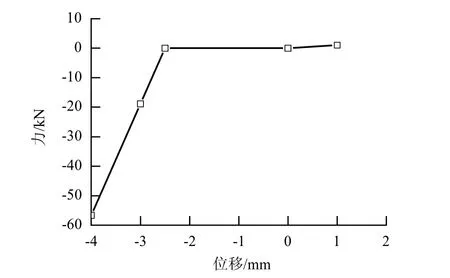
圖2 非線性彈簧單元的力-位移曲線Fig.2 Force-displacement curve of the nonlinear spring element

1.2 Ⅰ型板式軌道動力學方程

車輛-Ⅰ型板式軌道垂向耦合動力學模型的計算方程由車輛及軌道結構兩部分組成，因篇幅限制，在此僅列出鋼軌及Ⅰ型軌道板的垂向動力學方程［4-5］.

鋼軌的4 階偏微分振動方程為

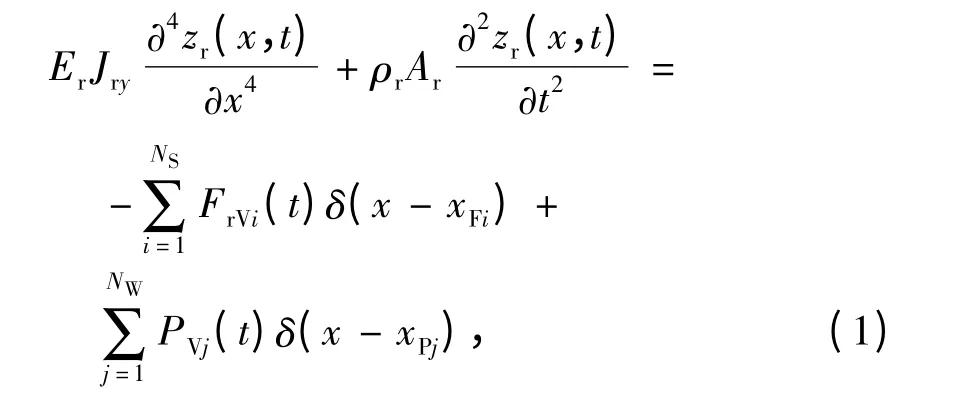
式中:

Er為鋼軌的楊氏模量;

Ar、ρr為鋼軌的截面積、質量密度;

Jry為鋼軌截面對水平軸的慣性矩;

NS、NW為鋼軌計算長度范圍內的軌枕數、輪軸數量;

FrVi為鋼軌第i 個支點的垂向反力;

PVj為第j 個車輪作用于鋼軌的垂向力;

xPj為鋼軌第j 個輪對的x 坐標.

為了進行數值分析，采用Ritz 法，引入鋼軌正則振型坐標qZk(t)，將上述4 階偏微分方程變換為式(2)所示的鋼軌振動的二階常微分方程組:

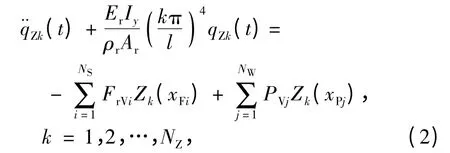
式中:Iy為y 向慣性矩;

l 為軌道有效計算長度;

NZ為鋼軌的垂向截止模態階數;

Zk為鋼軌的垂向振型函數，

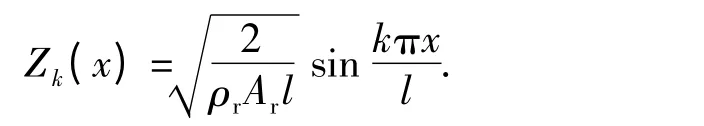
根據彈性薄板的振動理論，軌道板的垂向4 階偏微分振動方程為

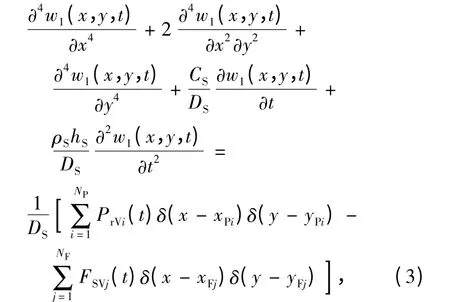
式中:w1(x，y，t)為軌道板的垂向撓度;

xPi、yPi為軌道板上第i 個鋼軌扣結點縱向及橫向位置坐標;

xFj、yFj為軌道板下第j 個支承點沿長度和寬度方向的坐標;

NP為軌道板上左右兩股鋼軌總扣結點數;

NF為軌道板下離散支承點數;

PrVi為軌道板上第i 個鋼軌結點的垂向反力;

FSVj為軌道板下第j 個支承點的垂向反力;

hS為軌道板的厚度;

ρS為軌道板的質量密度;

CS為軌道板的阻尼系數;

DS為軌道板的彎曲剛度.

采用分離變量法，引入軌道板的正則振型坐標Tmn(t)，可得軌道板垂向振動關于正則坐標的二階常微分方程為

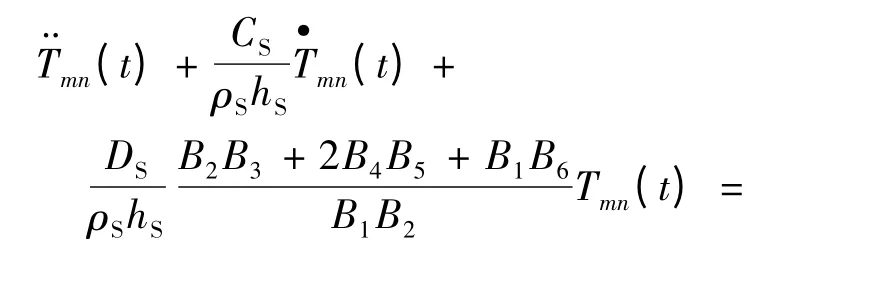
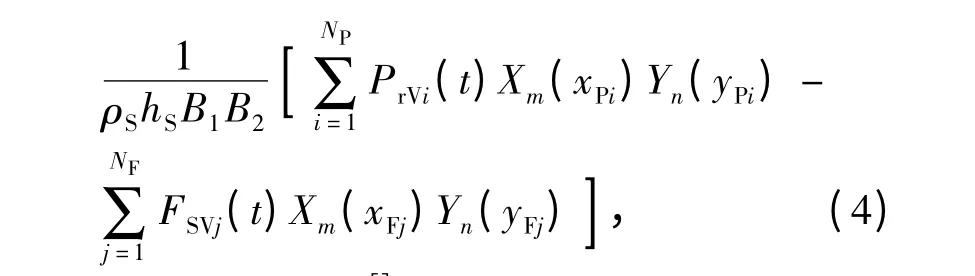
式中:B1～B6為參數［5］;

m=1，2，…，N1x; n=1，2，…，N1y.

2 計算參數

計算模型中的車輛采用CRH2 型機車，具體參數參考文獻［5］，在實際計算中列車速度取為350 km/h.Ⅰ型軌道結構的具體參數如下:

鋼軌 采 用CHN60 軌，彈 性 模 量 為2.1 ×105MPa，泊松比為0.3;

軌道板長、寬、高分別為4.90、2.40、0.19 m;

混凝土標號為C50，彈性模量取為3.5 ×104MPa，泊松比為0.2，密度為2 500 kg/m3;

扣件系統豎向支承剛度取為60 kN/mm，垂向阻尼為75 kN·s/m;

CA 砂 漿 層 厚0. 05 m，彈 性 模 量 為3. 0 ×102MPa;

底座板寬度3. 0 m，高度0. 3 m，泊松比為0.2，密度為2 500 kg/m3;

下部基礎支承剛度1.0 ×103MPa/m，支承阻尼100 kN·s/m.

輪軌接觸彈簧的作用是聯系、耦合車輛系統和軌道結構兩個振動子系統.由于非線性赫茲接觸彈簧會大大增加動力分析的難度，并且輪軌接觸彈簧剛度誤差不會顯著影響動力計算的結果［10］.因此，本文的模型中將輪軌接觸彈簧進行線性化處理.

高速鐵路軌道結構的主要幾何不平順為無縫線路焊接接頭處的凹凸不平順，因此，本文采用焊縫凹接頭不平順來模擬軌道幾何不平順，實際計算時，在波長為1 m 的余弦波上疊加波長為0.1 m 的短波來表示不平順，其函數表達式為

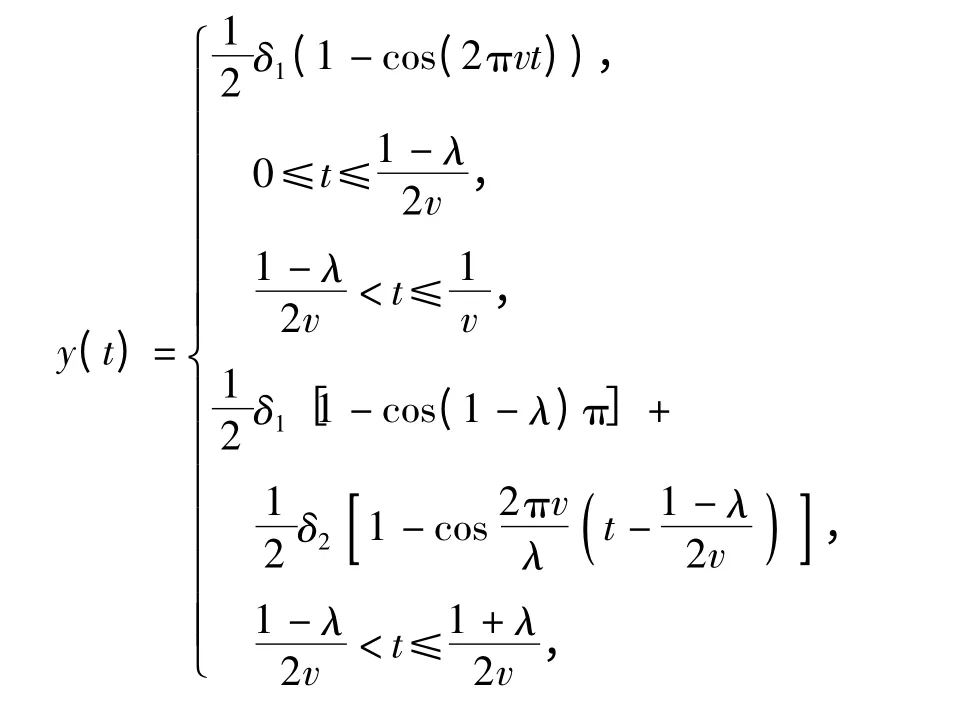
式中:

δ1、δ2為長波和短波波幅，m;

v 為行車速度，m/s;

λ 為短波波長，m.

計算模型中，焊接凹接頭不平順施加在離縫區軌道板上方的鋼軌梁上，以模擬接頭不平順及離縫疊加現象對軌道結構及車輛的動力影響.

3 模型的驗證

為評定本文建立的車輛-Ⅰ型板式軌道垂向耦合動力學模型計算結果的準確性，采用文獻［11］中的Ⅰ型板式軌道主要部件參數作為初始條件，計算了列車速度取為200 km/h 時，Ⅰ型板式軌道結構的各項力學響應，計算結果與西南交通大學在遂渝線實測結果的對比見表1.

從表1 可以看出，用本文建立的計算模型獲得的計算結果與實測結果比較接近，說明本文建立的動力學模型是正確的.

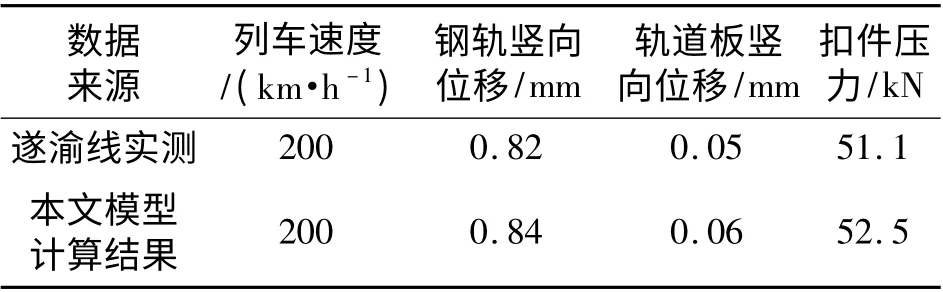
表1 本文模型計算結果與實測結果對比Tab.1 Comparison between the calculated results of the model and test results

4 板端離縫對各評價指標的影響

在各線路實地調研時發現，離縫長度多數為1 m 左右，離縫高度多數為2 mm 左右，因此，本文從離縫長度0.2 m 開始，以步長0.2 m 等差遞增至1.0 m，從離縫高度0.5 mm 開始，以步長0.5 mm等差遞增至2.5 mm. 通過將確定的離縫長度及高度工況進行組合，來模擬板端離縫發展的不同工況.

4.1 軌道板豎向位移

表2 為各種板端離縫工況下軌道板的最大豎向位移.由表2 可知，在各種工況下，離縫區軌道板均出現了脫空現象，且離縫長度越短，脫空現象越容易出現. 離縫長度為0. 2 m 時，離縫高度由0.5 mm 增加到2.5 mm，軌道板的豎向位移沒有發生變化，出現這種結果的原因是，在5 種離縫高度工況下，離縫區軌道板均是脫空受力. 離縫長度為1.0 m 時，在離縫高度不大于1.5 mm 的3 種工況下，軌道板的豎向位移隨離縫高度的增加而增加;在離縫高度大于1.5 mm 時的2 種工況下，軌道板的豎向位移保持一致.這是因為在5 種離縫高度工況下，軌道板最大位移為1.72 mm，離縫高度不大于1.5 mm 時的3 種工況下，離縫區CA 砂漿層會在有列車荷載作用時對軌道板提供支承作用;離縫高度大于2.0 mm 后，離縫區軌道板均是脫空受力.由表2 可知，離縫長度分別為0.4、0.6、0.8 m時，對應的軌道板脫空受力的離縫高度分別為0.63、1.03、1.25 mm，該值即為相應離縫長度下軌道板的豎向最大位移.

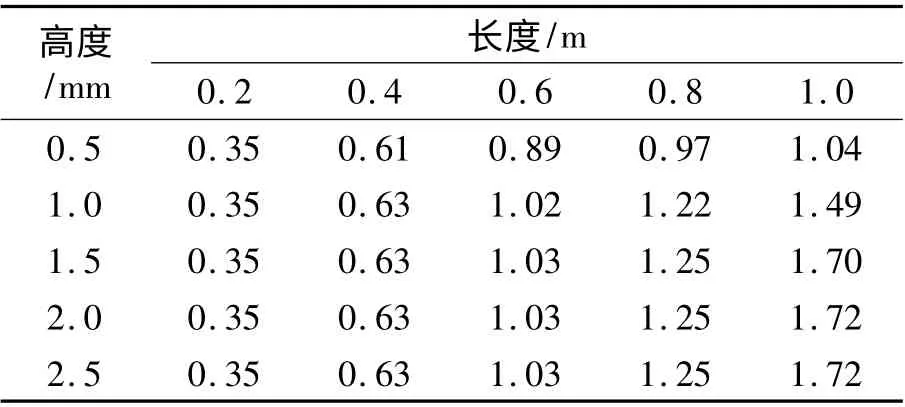
表2 軌道板的豎向位移Tab.2 Vertical displacement of track slab mm

4.2 輪軌力

輪軌垂向力用于評定輪軌之間的動作用力，過大的輪軌垂向力不僅會對鋼軌、扣件、軌道板等部件造成損傷及破壞，而且會導致軌道不平順急劇增大，增加線路養護維修工作量和費用，嚴重時還將危及行車安全.

在各種板端離縫工況下，輪軌力的變化如圖3所示.離縫長度一定時，離縫高度G 的變化對輪軌力幾乎沒有影響.當離縫長度為0.2 m 時，輪軌力達到最大值182 kN.

當離縫長度不大于0.6 m 時，輪軌力隨離縫長度的增加而有所減小;當離縫長度大于0.6 m 后，輪軌力隨離縫長度的增加又緩慢增加.但是離縫長度從0.2 m 增加到1.0 m，輪軌力的最大變化幅度僅為1.9 kN，約為最大輪軌力的1%.

同時，CRH2 型車輛以350 km 的時速通過無板端離縫現象的Ⅰ型軌道結構(有焊接不平順)時，輪軌動作用力約為177 kN，而圖3 中各種離縫工況下的輪軌力最大值為182 kN，即由于離縫現象的存在，輪軌動作用力增加了5 kN，約為無離縫現象時輪軌動作用力的2.8%.

因此，由以上分析可知，離縫長度的變化對輪軌力大小有一定影響，但效果不明顯.

4.3 軌道板拉應力

各種板端離縫工況下，軌道板最大拉應力變化如圖4 所示.當離縫長度不大于0.4 m 時，應力值隨離縫高度的增加先增后減;當離縫高度為1.5 mm 時，應力達到最大值. 當離縫長度大于0.4 m 后，離縫高度由0.5 mm 增加到1.5 mm 時，應力值增加明顯;當高度大于1.5 mm 后，應力值增加緩慢.

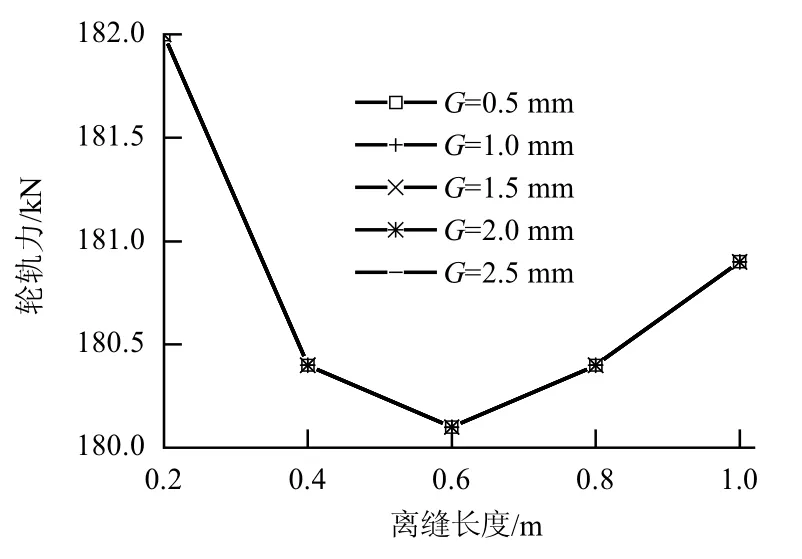
圖3 輪軌力Fig.3 Forces of wheel and rail

［12］，考慮到Ⅰ型軌道板為縱橫雙向預應力結構，本文軌道板拉應力容許值取為5.9 MPa，以該值為標準，本文計算的各種離縫工況中，除離縫高度為0.5 mm 的5 種工況，以及離縫高度為1.0 mm、離縫長度為0. 2 和0. 4 m 的2 種工況外，其余工況下的軌道板拉應力均超過該容許值.因此，為使軌道板拉應力值不超過容許值，板端離縫長度應控制在0.4 m 以內，離縫高度應控制在1.0 mm 以內.

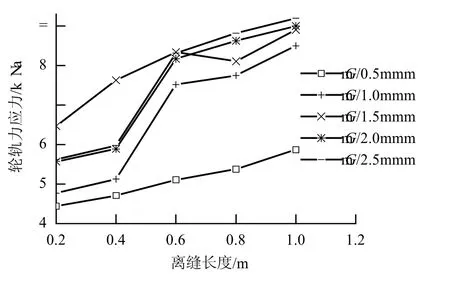
圖4 軌道板應力值Fig.4 Stresses of slab

4.4 軌道板加速度

各種板端離縫工況下，軌道板加速度的變化規律如圖5 所示.當離縫長度為0.2 m 時，軌道板加速度不受離縫高度的影響;當離縫長度大于0.4 m時，離縫區軌道板加速度均隨離縫高度的增加而緩慢減小.值得注意的是，離縫長度從0.2 m 增加到0.4 m 時，軌道板加速度增加了185 m/s2;離縫長度從0.4 m 增加到1.0 m 時，軌道板加速度僅增加了21 m/s2. 表 明 在 離 縫 長 度 從0. 2 m 增 加 到0.4 m 時，軌道板加速度有較大的突變，加速度突變不僅會惡化軌道板受力狀態，而且會加劇CA 砂漿的破壞，因此，為避免軌道板加速度的突變，板端離縫長度不應大于0.2 m.

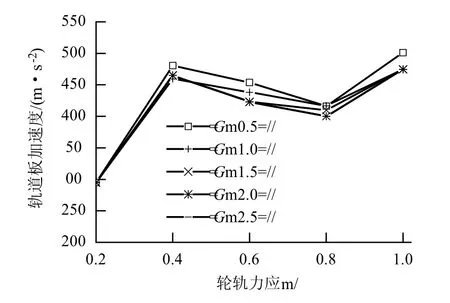
圖5 軌道板加速度Fig.5 Accelerations of slab

4.5 鋼軌位移及加速度

鋼軌豎向位移及加速度用于評定鋼軌的動態變形，鋼軌豎向位移及加速度變化過大，均會對旅客乘坐舒適性、機車車輛的輪對及轉向架等部件造成損傷，且鋼軌加速度是影響軌道結構振動和輪軌噪聲的關鍵因素.

由圖6 可知，當離縫長度不大于1.0 m 時，離縫長度一定，離縫高度的變化對鋼軌豎向位移幾乎沒有影響;離縫長度為1.0 m 時，離縫高由0.5 mm增加到2. 5 mm 時，鋼軌豎向位移也僅增加0.07 mm.這表明離縫長度一定，離縫高度變化對鋼軌豎向位移幾乎沒有影響，這主要是因為高速列車荷載對鋼軌作用時間很短，而這種瞬時的高頻振動和沖擊主要由扣件的豎向彈性和阻尼進行了緩沖.離縫高度一定，鋼軌豎向位移隨離縫長度的增加均有較明顯的增加.

由圖7 可知，當離縫長度一定，離縫高度的變化對鋼軌加速度也幾乎沒有影響，離縫高度一定，板端離縫長度由0.2 m 增加到1.0 m 時，鋼軌豎向加速度增加了約13 m/s2，說明，鋼軌加速度隨離縫長度的增加也有較明顯增加.

輪軌噪聲主要由輪軌之間相互作用產生的振動向外輻射聲波造成，因此，隨離縫長度增加而增加的鋼軌豎向加速度，不僅對車體及軌道結構的穩定性及耐久性造成影響，同時還會產生更多的輪軌噪聲，影響舒適度性能.

總體而言，離縫長度是影響鋼軌豎向位移及加速度的主要因素.

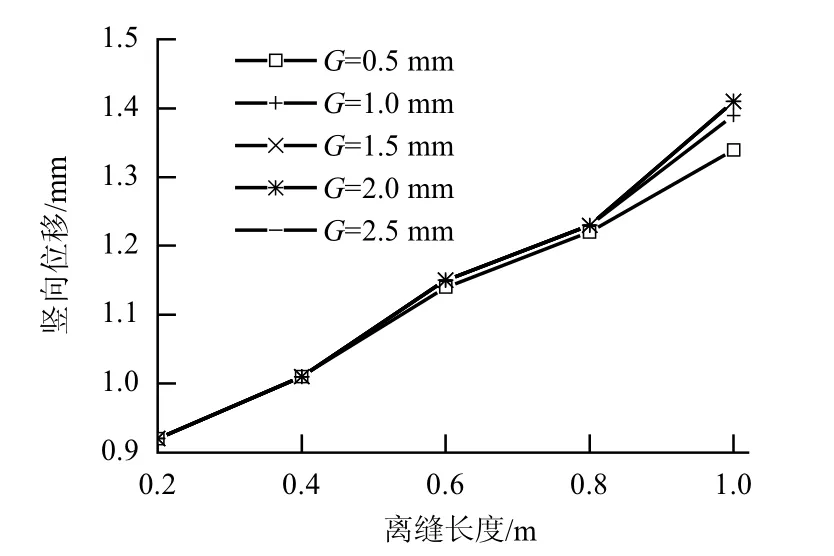
圖6 鋼軌豎向位移Fig.6 Vertical displacements of rail

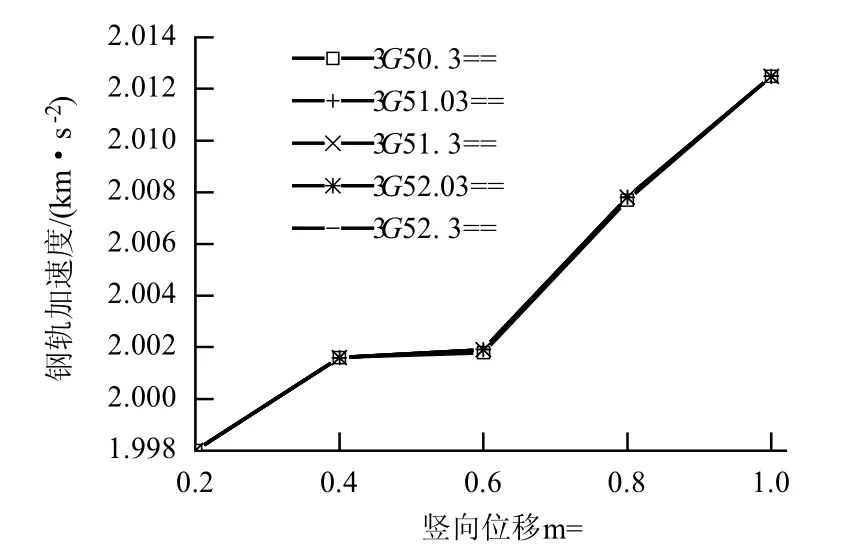
圖7 鋼軌加速度Fig.7 Vertical accelerations of rail

4.6 車體加速度

車體加速度是列車運行平順性的重要指標，車體加速度過大會加速車輛-軌道系統部件的損傷，并嚴重影響高速列車運行的安全性和可靠性.在各種板端離縫工況下，車體加速度變化如圖8 所示.

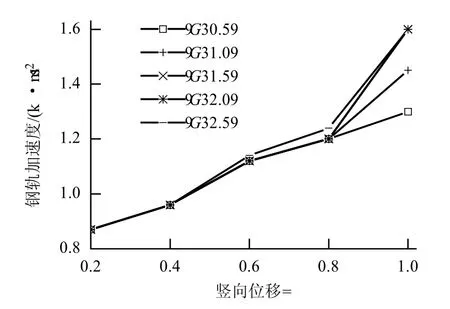
圖8 車體加速度Fig.8 Accelerations of vehicle

當離縫長度不大于0.8 m 時，離縫長度一定，離縫高度的變化對車體加速度幾乎沒有影響;當離縫長度大于0.8 m 時，離縫高度的變化對車體加速度有一定的影響，離縫高度不大于1.5 mm 時，車體加速度從1.3 m/s2增加到1.6 m/s2，而離縫長度大于1.5 mm 后，車體加速度保持為1.6 m/s2不再增加.

《高速鐵路設計規范》［13］中規定:車體豎向振動加速度不能大于1.3 m/s2. 在本文的計算中，離縫長度達到1.0 m 時的5 種工況下，車體的豎向振動加速度均大于1.3 m/s2，說明這幾種工況均使得車體振動加速度超過規范的規定值. 實際上，從圖8 可知，當離縫長度不大于0.8 m 時，車體振動加速度最大為1.1 m/s2;當離縫長為0.8 m 時，即使離縫高度僅為0.5 mm，車體振動加速度也達到了1.2 m/s2，若考慮軌道或車體的其他不良因素的影響，車體振動加速度有可能已經超過規范的規定值，因此，為了使車體振動加速度不超過容許值，建議板端離縫長度不應大于0.6 m.

5 結 論

通過建立的車輛-Ⅰ型板式軌道的垂向耦合動力學模型，研究了不同工況下的板端離縫對軌道結構及車輛力學性能的影響，得出的主要結論如下:

(1)板端離縫長度越短，軌道板越容易脫空受力.軌道板脫空受力時的離縫高度即為該離縫長度下板的豎向最大位移.

(2)相對離縫高度而言，離縫長度對輪軌力、軌道板位移、拉應力及加速度、鋼軌位移及加速度、車體加速度的影響更大.

(3)長度不大于0.6 m 的板端離縫主要使軌道結構的變形及受力狀態惡化;離縫長度大于0.6 m 后，車輛的振動加速度超過了容許值，說明長度大于0.6 m 的板端離縫也降低了車輛運行時的平順性能.

致謝:西南交通大學青年教師百人計劃資助項目(SWJTU09BR277).

參考文獻:

［1］ 楊俊斌，劉學毅，梁東，等. CRTS Ⅰ型軌道板中部砂漿離縫對軌道豎向變形與受力研究［J］. 鐵道標準設計，2013(6):22-24.YANG Junbin，LIU Xueyi，LIANG Dong，et al. The influence on track vertical deformation and stress state caused by seamed mortar layer in the middle of CRTS-Ⅰtrack slab［J］. Railway Standard Design，2013(6):22-24.

［2］ 劉鈺，趙國堂. CRTS Ⅱ型板式無砟軌道結構層間早期離縫研究［J］. 中國鐵道科學，2013，34(4):1-6.LIU Yu，ZHAO Guotang. Analysis of early gap between layers of CRTS Ⅱslab ballastless track structure［J］.China Railway Science，2013，34(4):1-6.

［3］ 徐浩，劉霄，徐金輝，等. 溫度作用下軌道板與CA 砂漿離縫對CRTSⅡ型板式軌道的影響分析［J］. 鐵道標準設計，2013(9):9-12.XU Hao，LIU Xiao，XU Jinhui，et al. Influence on CRTS Ⅱslab track structure caused by the debonding between slab and CA mortar under the action of temperature load［J］. Railway Standard Design，2013(9):9-12.

［4］ 劉學毅. 車輛-軌道-路基系統動力學［M］. 成都:西南交通大學出版社，2010:30-101.

［5］ 翟婉明. 車輛-軌道耦合動力學［M］. 北京:科學出版社，2007:12-38.

［6］ 尚曉江，蘇建宇，王化鋒，等. ANSYS/LS-DYNA 動力分析方法與工程實例［M］.北京:中國水利水電出版社，2008:50-156.

［7］ 王新敏. ANSYS 工程結構數值分析［M］. 北京:人民交通出版社，2007:33-55.

［8］ 劉濤，楊鳳鵬. 精通ANSYS［M］. 北京:清華大學出版社，2002:303-307.

［9］ 龔曙光，謝桂蘭，黃云清. ANSYS 參數化編程與命令手冊［M］. 北京:機械工業出版社，2010:87-100.

［10］ 周毅. CRTSIII 型板式軌道減振特性研究［D］. 成都:西南交通大學，2011.

［11］ 羅震. 高速鐵路無砟軌道結構受力及輪軌動力作用分析［D］. 成都:西南交通大學，2008:30-50.

［12］ 徐慶元，李斌，周智輝. CRTS-Ⅰ型板式無砟軌道線路路基不均勻沉降限值研究［J］. 中國鐵道科學，2012，33(2):1-6.XU Qingyuan，LI Bin，ZHOU Zhihui. Study on the limited value for the uneven settlement of subgrade under CRTS-Ⅰtype slab track［J］. China Railway Science，2012，33(2):1-6.

［13］ 鐵道第三勘察設計院集團有限公司，中鐵第四勘察設計院集團有限公司，中國鐵道科學研究院. 高速鐵路設計規范［S］. 北京:中國鐵道出版社，2009.