鋼筋混凝土橋梁結構橫向塑性倒塌分析

黃華

（上海市政工程設計研究總院（集團）有限公司武漢分院，湖北武漢 430077）

0 引言

橋梁工程為生命線工程(一般指城市供水、供電、供氣、電信、交通等基礎設施)之一,而其破壞造成震后救災工作的巨大困難,使次生災害加重。特別是對現(xiàn)代化城市,將影響生產的正常運轉,導致巨大的經(jīng)濟損失，因此,對橋梁結構進行抗震分析意義重大。對橋梁結構作抗震性能的全面評估，應包括縱向地震作用與橫向地震作用下結構的抗震性能，目前常用的分析方法是采用非線性地震反應分析方法，并從能力設計原則對結構的抗震性能進行綜合評價[1]。

橋梁結構作為一個完整的受力體系，在地震作用下其破壞是從局部開始的，尤其是下部結構的破壞會直接導致承載能力完全喪失后落梁、倒塌等事故。對橋梁結構的抗震分析主要是對下部墩柱抗震性能的研究，目前常用的分析方法包括線彈性反應譜法、彈塑性動力時程分析法、等效靜力分析法（Push-over）等。橋梁結構的塑性倒塌分析方法是近年來應用比較廣泛的一種非線性塑性倒塌機理分析方法，通過分析結構的非線性變形能力來評價它的抗震能力。塑性倒塌分析在對逐個橋墩進行塑性倒塌分析的基礎上，將各墩用剛性的上部結構相連接，通過計算對應于不同極限狀態(tài)（正常使用極限狀態(tài)、結構最終極限狀態(tài)）的等效彈性反應慣性力及地震加速度，再與設計反應譜或橋址處的實際反應譜加速度進行比較，從而判斷橋梁結構的安全性及抗震能力。該方法與通常的非線性動力分析相比，具有計算簡單、結果明確等優(yōu)點。

1 橋墩的荷載-變形關系及延性能力

一般而言，橋墩承受單位水平向地震力作用時，其地震力中心處總變位δ可分解為橋墩自身彈性彎曲變位δ1、由彈性基礎平動產生的變位δ2 以及轉動產生的變位δ3。上述各項相對于地震力中心處的剛度分別為：

故地震力中心處橋墩等效剛度為：

式中：K2、K3 可根據(jù)“m 法”來計算確定；K1 為橋墩自身水平抗推剛度。

式中：My、Mu為鋼筋混凝土橋墩墩底截面屈服彎矩、極限彎矩；φy、φu為鋼筋混凝土橋墩墩底截面屈服曲率、極限曲率；Δy、Δu為地震力中心處結構的屈服位移、極限位移。Lp（φu-φy）（h-0.5Lp）；h 為墩底至地震力中心處的高度；Lp 為墩底等效塑性鉸長度，一般按擬靜力試驗得到的經(jīng)驗公式計算。

墩底截面的屈服（極限）彎矩、屈服（極限）曲率可采用專業(yè)軟件 UCFyber 程序，將鋼筋混凝土截面離散為一系列的纖維單元來進行彎矩曲率（P-M-φ）分析得到（見圖1）。其中，約束混凝土的本構關系可采用 Mander 模型建立[3]，鋼筋取為理想彈塑性材料，采用理想雙線型本構模型（Bilinear steel mode）。

圖1 墩底截面 M-φ

2 塑性倒塌分析

根據(jù)上節(jié)確定的橋墩等效抗推剛度，將各墩用上部結構聯(lián)系成整體，各墩簡化成初始剛度與橋墩抗推剛度相同的彈簧進行塑性倒塌分析。圖2為變形后的結構體系。

圖2 變形后的結構體系

（1）體系彈性工作階段

當各墩均尚未屈服時（彈性工作階段），在橋梁質心處作用單位地震荷載 P=1，則在剛度中心處受到 P=1 的橫向力以及 M=y的彎矩。

對 Ck點取力矩平衡，有，即：

體系質心處位移：

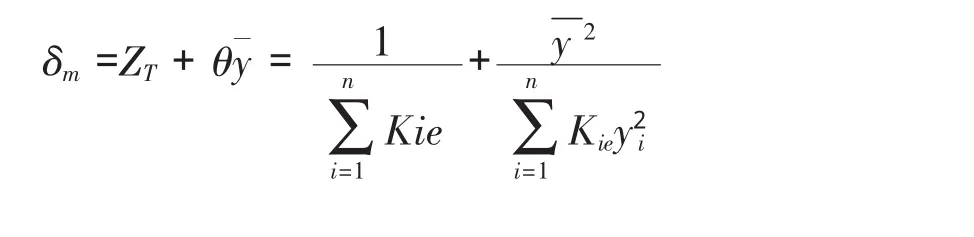
則任一橋墩 i 地震力中心處位移為：

（2）體系塑性工作階段

當體系進入塑性工作狀態(tài)，因屈服后體系剛度中心不斷變化，對體系進行倒塌分析時必須跟蹤各墩剛度變化，不斷調整剛度中心及體系有效剛度。設在質心處作用地震荷載 P 時，第 i+1 號至第 n 號墩屈服，屈服剛度為 K*i+1～K*n。

屈服后橋墩當產生 δ（jj=i+1,…n）的位移時，相應產生的荷載為：

由結構體系平動內力平衡∑Z=0，可得：

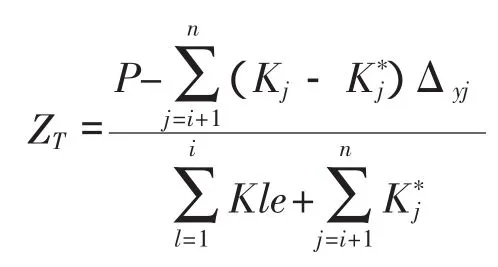
由∑M=0，可得轉角：

式中：l=1,…i，j=i+1,…n。

故任一橋墩 i 地震力中心處位移為：

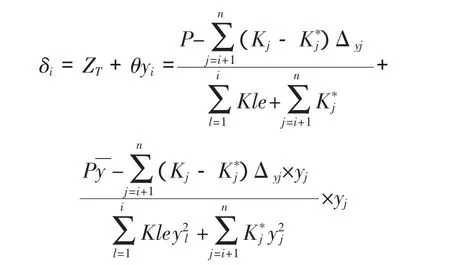
若簡化計算，考慮屈服后剛度為零，即 Kj*=0，則：

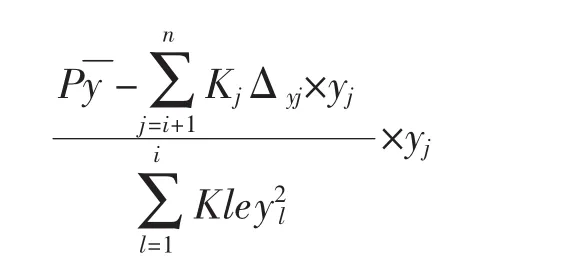
此時地震荷載 P 為結構的實際地震反應時各墩的荷載之和。由于結構的延性，結構的最終極限狀態(tài)的等效彈性地震荷載可根據(jù)結構的延性系數(shù)采用等位移原理確定：

（3）等效彈性地震荷載的修正

對于長周期橋梁采用等位移假定是可行的，而對于短周期橋梁采用等位移假定求解就偏于不安全了。對周期不同的結構可采用新西蘭規(guī)范的折減系數(shù)進行修正[2]：

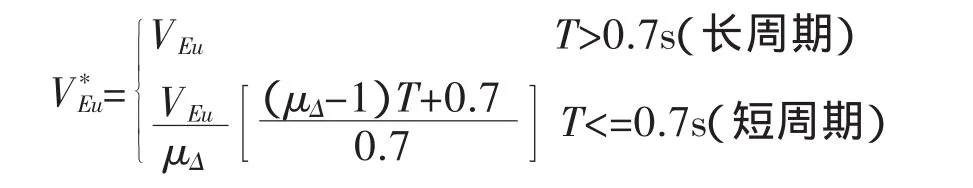
因此，結構所能承受的對應最終倒塌極限狀態(tài)的等效地震加速度為：

通過將 Sau與設計反應譜或實際計算的橋址場地反應譜中對應的加速度進行比較，可確定結構的安全性和抗震能力。

3 工程實例分析

某城市三跨變截面連續(xù)箱梁橋跨布置為 34 m+55 m+34 m=123 m，上部結構為高 1.7～3.3 m 單箱四室箱梁，橋面寬度 22.5 m；橋墩為實體式矩形板墩，長 14 m，寬 2.2 m，墩高均為 8 m，墩頂均采用盆式橡膠支座。根據(jù)地質勘察報告，橋址處地震設防烈度為 7 度，設計基本地震加速度值為 0.15 g。橋梁結構的主要設計參數(shù)見表1。

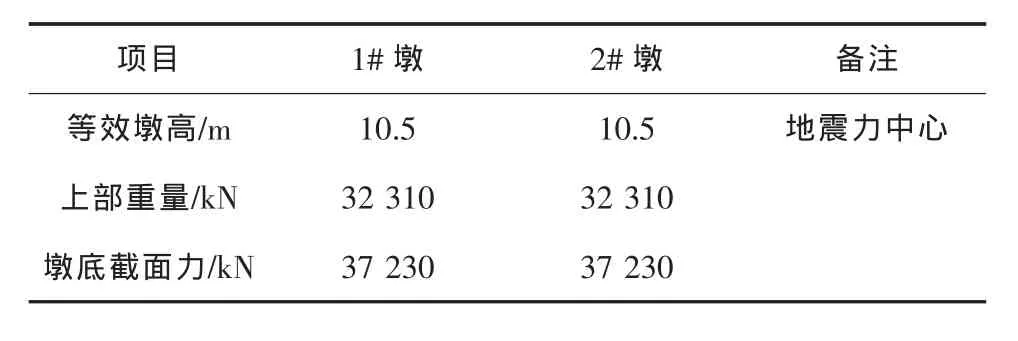
表1 橋梁結構主要設計參數(shù)（墩柱）

橋墩采用 C40 混凝土，其換算圓柱體混凝土抗壓強度 f’c=34 MPa；墩身內主筋及箍筋均采用HRB335 級，主筋直徑 28 mm，箍筋直徑 12 mm；主筋屈服應變εy=0.001 9，屈服強度 fy=335 MPa；箍筋屈服強度 fyh=335 MPa，體積配箍率ρx=0.003 8，ρy=0.005 1，箍筋在最大拉應力時的應變εsu=0.09；混凝土的極限壓應變經(jīng)計算得εcu=0.013。

根據(jù)專業(yè)軟件 UCFyber 程序采用纖維模型分析計算得到橋墩 M-φ曲線（見圖3），可以確定各墩主要計算參數(shù)（見表2），為便于分析，將橋墩的彎矩-曲率關系簡化為雙線性關系，屈服后剛度取為零。

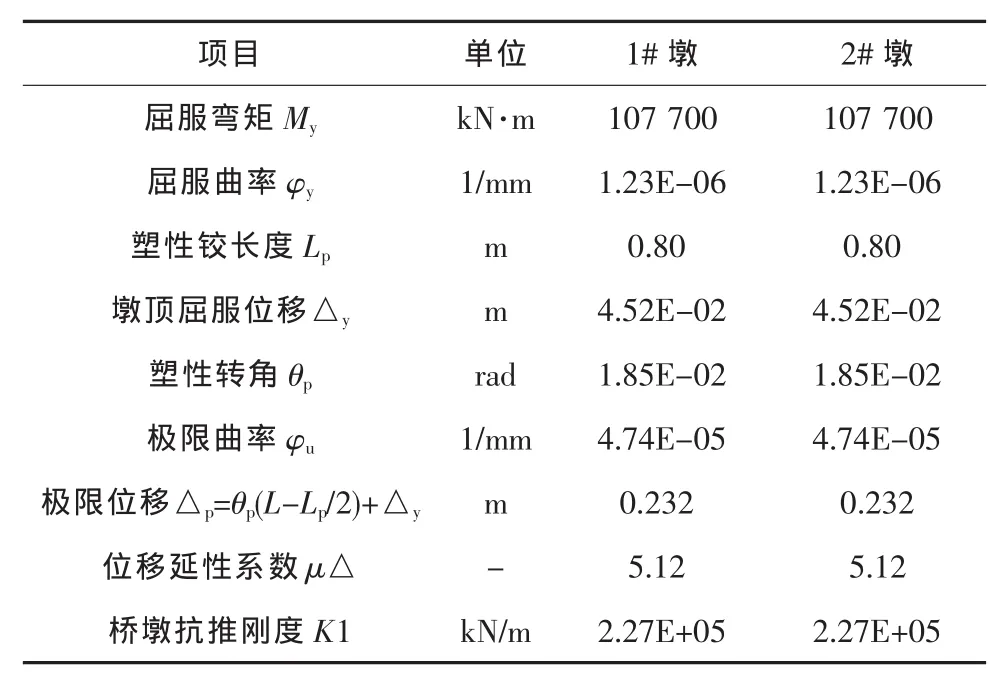
表2 橋墩主要計算參數(shù)

考慮彈性地基柔度后（地基柔度根據(jù)“m”法計算確定），結構等效彈性剛度經(jīng)計算可得：

由以上分析及表3結論可知，該橋采用了實體式板墩，整體剛度較大。該橋結構體系達到屈服時所承受的等效地震加速度為 0.196 g(大于0.15 g)，達到了 7 度抗震設防的要求；在 8 度地震作用下，各橋墩均進入屈服狀態(tài)，但不至倒塌。

表3 橋梁抗震性能評估

4 結語

本文通過建立橋梁橫橋向抗震性能評估的塑性倒塌分析模型，通過計算對應于不同極限狀態(tài)的等效彈性反應慣性力及等效地震加速度，對橋梁結構在地震作用下的安全性及抗震能力作出評價。該方法與通常的非線性動力分析相比，具有計算簡單、結果明確等優(yōu)點。

在橋墩延性抗震設計中，應充分考慮土與橋梁結構的相互作用，計算分析應盡量與地震作用下的真實情況相一致。雖然樁土效應對結構體系的延性變形性能的影響不大，且結構剛度的減小雖然增長了結構周期，但結構的整體抗震能力仍有所下降，必須得到足夠的重視。

[1] 范立礎,卓衛(wèi)東.橋梁延性抗震設計[M].北京:人民交通出版社,2001.

[2] 范立礎,李建中,王君杰.高架橋梁抗震設計[M].北京:人民交通出版社,2001

[3] CJJ 166-2011.城市橋梁抗震設計規(guī)范[S].

[4] 代本明.箍筋約束混凝土橋墩延性與柱支梁橋抗震性能研究[D].南京：東南大學,2007.