東江系桿拱橋穩定性分析

王曉琴 ，路 韡

（1.西北民族大學土木工程學院，甘肅蘭州 730000；2.蘭州交通大學土木工程學院，甘肅蘭州 730070）

0 引言

穩定問題是橋梁工程中經常遇到的問題，與強度問題有著同等重要的意義。梁拱組合式橋梁的穩定性與施工過程和結構形式有密切關系，其失穩形式分為兩類，平面內失穩與空間側面失穩[1]。

帶有橫撐的雙肋系桿拱橋，拱間橫撐和吊桿的非保向力作用使系桿拱橋的側向穩定承載力比上承式拱橋或無橫撐系桿拱橋大很多，但同時考慮橫撐和吊桿時，使問題的研究呈現一定的復雜性，因此對有橫撐系桿拱橋側向穩定性的研究，有助于穩定承載力的計算和結構形式的選擇，具有工程意義和實用價值。

1 計算理論

對于系桿拱橋的穩定性問題，結構最不安全狀態不一定出現在橋梁的運營階段，相反起控制作用的力學狀態往往出現在施工階段，因此對施工階段結構的穩定性分析就顯得十分必要。文獻[2]基于能量原理推導了有橫撐系桿拱橋側向彈性穩定承載力的解析計算公式，在公式中考慮了橋梁跨度、矢跨比、拱肋截面側向抗彎剛度與抗扭剛度、橫撐截面剛度、肋間距和橫撐數目等因素的影響，在公式推導過程中假設拱軸線為圓弧形、橋面系側向抗彎剛度很大等，在使用過程中是具有局限性的。使用有限元原理，對系桿拱橋建立全橋模型，并可對其各個施工過程進行穩定性分析，計算原理如下[3]。

1.1 第一類失穩問題

系桿拱橋第一類失穩問題屬于平衡分支問題，其本質是數學上的特征值問題，求解出的最小特征值就是拱橋的失穩臨界荷載系數，線性求解方程為：

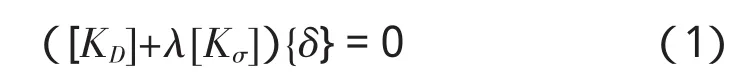
式中：[KD]為結構彈性剛度矩陣；[Kσ]為結構初始應力剛度矩陣；λ為拱橋荷載穩定系數；δ為結構的位移增量。

由上述方程計算出的特征值只有其最小值才有實際意義，最小值對應的就是失穩的臨界荷載系數。

1.2 第二類失穩問題

系桿拱橋第二類失穩問題屬于極限點失穩問題，可通過幾何非線性分析、纖維模型的動力彈塑性分析來實現，計算過程中采用平衡迭代的方法進行。

式中：[KL]為結構大位移剛度矩陣；{F}為結構等效節點處荷載值。

壓潰荷載即是考慮拱橋幾何材料雙重非線性所得的極限失穩荷載。

2 計算實例

2.1 工程簡介

東江系桿拱橋位于甘肅省隴南地區，結構形式為 50 m 下承式鋼筋混凝土簡支系桿拱橋。計算矢高 10 m，矢跨比 1/5，橋面結構采用縱橫梁體系、整體橋面板。主梁預應力 A 類構件設計，其它結構按鋼筋混凝土截面設計。全橋共設 11 道預應力混凝土橫梁，其中有 2 道端橫梁、9 道中橫梁。拱肋合攏溫度按 15℃考慮。全橋布置 9 對吊桿，吊桿間距為5.0 m。全橋共設兩榀鋼筋混凝土拱，拱肋與加勁縱梁固結，兩榀拱肋橫向間距為 18.5 m，在拱肋設置3 道鋼管風撐。結構按地震烈度Ⅷ設防，設計荷載為城-A 級，設計車速為 50 km/h。

施工過程為先在支架上進行梁體、拱肋施工，然后張拉吊桿進行結構體系轉換，吊桿張拉順序見表1。橫撐何時安裝需進一步討論，故本文分別分析了張拉前安裝橫撐與張拉后安裝橫撐兩種情況。

表1 東江系桿拱橋吊桿張拉順序

2.2 計算模型

對東江系桿拱橋的計算使用商用有限元軟件Midas Civil 為分析平臺，采用正裝分析法，模擬在施工過程中及成橋后結構的穩定性。在計算分析時可使用單元的“激活”、“鈍化”功能，一次性建好全橋結構模型，在以后每個工況的分析中，通過該功能定義各施工節段，以此來實現對整個施工過程的模擬計算。

對該橋建立空間桿系模型，全橋節點 89 個，單元 138 個。其中：主梁、拱肋為梁單元，吊桿為只受拉的索單元，拱肋與主梁采用剛臂單元連接，支架采用只受壓的彈性連接進行模擬，模型見圖1。

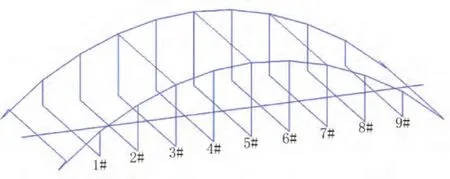
圖1 東江系桿拱橋有限元模型

3 數據分析

由圖2可見，在結構無橫撐時吊桿張拉過程中，隨著吊桿力的不斷增大，拱的穩定安全系數逐漸減小，并從第 6 工況起，穩定安全系數比現行規范要求拱橋的“結構穩定安全系數應大于 4～5”略低，從理論分析上不滿足要求[4]。第 9 工況穩定性系數達到最小值 3.49，而在此后的 3 個階段里，穩定安全系數又逐漸增大，最終達到 3.86。

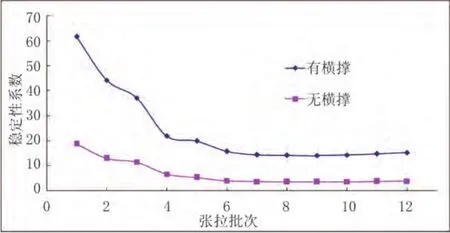
圖2 拱肋有、無橫撐時各工況穩定性系數對比

由圖2可見，在結構有橫撐的吊桿張拉過程中，隨著吊桿力的不斷增大，拱的穩定安全系數逐漸減小。由于在張拉過程中增設了 I 型支撐，穩定性系數大大提高，但在張拉吊桿的過程中拱的穩定性系數變化的范圍較大。與無橫撐一致，在第 9工況，穩定安全系數達到最小值 14.03，而在此后的 3 個階段里，穩定安全系數又逐漸增大，最終達到 15.26。第 9 工況的第一階失穩形態見圖3，拱肋以橫向屈曲為主，橋面不動。加上橫撐后，與不加臨時橫撐相比，拱的一階失穩形態發生了明顯變化，由橫向對稱屈曲變為橫向彎曲屈曲，其失穩形態見圖4。

圖3 拱肋無橫撐時工況9 第一階失穩形態

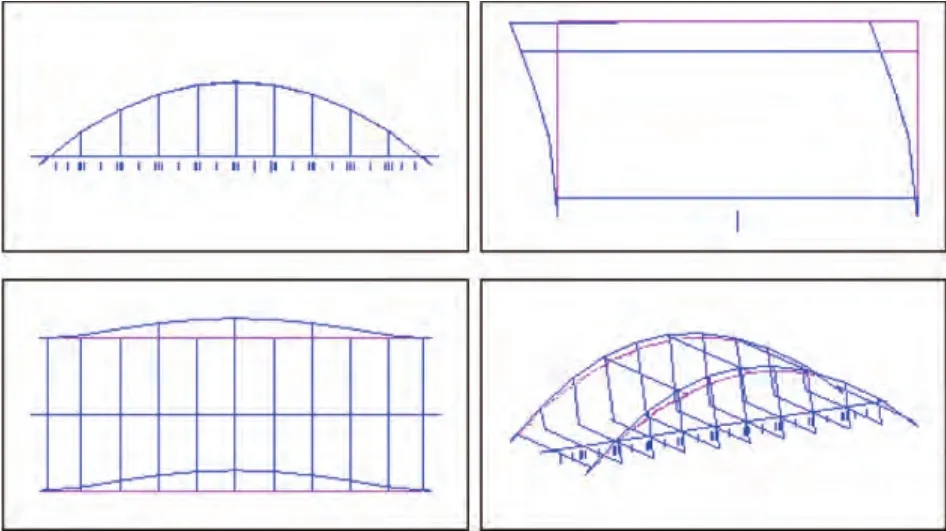
圖4 拱肋有橫撐時工況9 第一階失穩形態

在后 3 個施工階段里，穩定性系數均出現逐漸增大的情況，原因是由于后 3 個階段對吊桿的張拉屬于對整個吊桿力的微調階段，且跨中吊桿力是略微減小的，故穩定安全系數有所增大。

4 結論

本文采用有限元程序 Midas Civil 建立東江系桿拱橋模型，分析了該橋在不同工況下的穩定性，并比較了在施工過程中是否需要加入橫撐的狀況，得到以下結論：

（1）施工階段拱肋的穩定性通常低于成橋后的穩定性，并且平面外的穩定性常常是拱肋失穩的主要原因。設置橫撐可以大大提高結構的穩定性，本例可考慮在吊桿張拉前安裝全部或部分橫撐，防止結構因失穩發生破壞。

（2）非保向力對拱肋穩定性的影響有正面效應，也有負面效應，在分析時須同時考慮吊桿的內力和吊桿的非保向力對拱肋穩定性的綜合影響。本例中拱肋的穩定性下降并非是由于吊桿的負面效應，而是由于吊桿的作用力增大所致。

（3）合理地調整吊桿的張拉次序及張拉力可使拱的穩定安全性系數起伏較小，但怎樣找到張拉吊桿的理想方案尚需進一步加以研究。

[1] 邱文亮，張哲，范金軍.大跨度鋼管混凝土系桿拱橋施工方案研究[J].大連理工大學學報.2005,45(2):230-233

[2] 劉釗，呂志濤.有橫撐系桿拱橋的側向穩定承載力[J].工程力學，2004，21(3)：21-24.

[3] 鄭曉燕，周躍，瞿芹，等.PC 系桿拱橋施工階段穩定性及臨時橫撐影響分析[J].橋梁建設，2012，42(1)：67-70.

[4] JTG D62—2004,公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].