微積分證明題中的常數變易法

顧曉偉

（蘇州健雄職業技術學院現代港口與物流管理系，江蘇太倉215411）

顧名思義，常數變易法就是將某一常數換成變量，引入輔助函數證題的方法.此法在證明等式和不等式時有普遍應用.請看以下幾例：

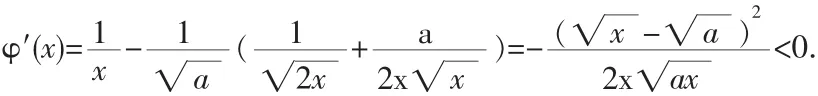
故當 x＞a 時,f(x)單調增加.又 f(a)=0,所以當 x＞a 時,f(x)＞f(a),

(x2+a2)(ln x-ln a)＞2a(x-a).從而當 b＞a＞0 時,有(b2+a2)(ln b-ln a)＞2a(b+a).即：

例 2 設 b＞a＞e,求證:ab＞ba.

[證明]考察 F(x)=x ln a-a ln x,a≤x＜+∞,F(x)在[a,+∞）可導,F(a)=0,

所以 F(x)在[a,+∞）單調上升,即 b＞a＞e 時有 F(b)＞F(a)=0,即 b ln a＞a ln b，

因此 b＞a＞e 時,ab＞ba.

例 3 設 f(x)在［0,+∞）連續.又 f(0)=0,f″(x)＜0(?x＞0),求證:對?x1＞0,?x2＞0,f(x1+x2)＜f(x1)+f(x2).

[證明]考察函數 F(x)=f(x)+f(x1)-f(x1+x),由 f′(x)＜0(?x＞0)知 f′(x)在x＞0 單調減少,故 f(x)＞f(x1+x)，即 F′(x)=f′(x)-f′(x1+x)＞0(?x＞0),所以 F(x)在 x＞0 單調上升,又 F(0)-f(0)=0,故 F(x)＞0(x＞0).因此?x2＞0,?x1＞0,有 F(x2)=f(x2)+f(x1)-f(x1+x2)＞0,即 f(x1+x2)＜f(x1)+f(x2).

例 4 設函數 f(x)在［0,1］連續,在（0,1）內可導,且 f(0)=0,0＜f′(x)＜1

例5 設f(x),g(x)均在［a,b］上連續,證明柯西不等式:

亦即：

例6 設f(x)連續，證明：

[分析]本題可用分部積分法或二重積分法證明。但若將a當作變量，由于當a=0時等式兩邊相等（均為零），只需檢驗二邊的導數相等.事實上，左邊導數為而右邊導數為.兩者相等，故原式成立.