基于測向測時差云閃定位精度分析及布局優(yōu)化

劉 洋，孫秀斌，盧 舟，王少娟

(成都信息工程學院電子工程學院，四川成都610225)

0 引言

閃電是發(fā)生于大氣中的災害性放電現象，放電過程中伴有大電流、高電壓和強電磁輻射，往往造成嚴重的財產損失和人員傷亡[1]。特別是近年來，隨著航空航天事業(yè)的發(fā)展，高層建筑的增多以及微電子技術的普遍運用，閃電造成的損失愈來愈嚴重。由于雷電災害的巨大破壞性和發(fā)生的不可阻止性，開展對閃電探測的研究是降低雷電災害損失的主要途徑。

根據閃電發(fā)生的位置，可將閃電分為云內閃電、云際閃電和云地閃電[2－3]。云地閃電又稱地閃，往往造成重大的人員傷亡和財產損失。云內閃電和云際閃電合稱為云閃，自然界中的大多數閃電都屬于云閃，但其造成的危害遠小于地閃。因為云閃在雷暴發(fā)生過程中先于地閃發(fā)生，同時也蘊含了更豐富的閃電信息，可以為雷電的監(jiān)測預警提供有力支撐，所以探測云閃具有更重要的科研價值[4]。

從閃電定位原理出發(fā)，利用測向測時差的無源定位方法對云閃進行定位。仿真了不同布站方式下的幾何稀釋精度(GDOP)等高線圖，并詳細分析了Y形布站方式下不同因素對定位精度的影響。

1 云閃定位方法及原理

云閃定位方法基本可以分為到達時間差法(Time Difference of Arrival，TDOA)、測向交叉法(Angle-of-Arrival，AOA)和測向測時差法(AOA/TDOA)[5－6]。到達時間差法至少需要4個站才能完成對云閃目標三維定位，并且對各站的測時精度要求較高，提高了探測系統(tǒng)的復雜性。測向交叉法僅需兩個探測站即可完成定位，但其測向精度受探測站附近地形地物影響較大，對天線的安裝環(huán)境要求較高，因此實際探測精度不是很高。測向測時差法是在時間差法的基礎上加入輻射源的方向信息以確定閃電發(fā)生的三維位置。這種方法在不提高系統(tǒng)復雜性的前提下，可以保證較高的定位精度，是較為理想的云閃定位方法。

云閃定位是通過采集云閃發(fā)生時輻射出的電磁脈沖信號的時間和角度信息，經過一系列的處理計算以確定閃電發(fā)生的位置和相關參數。利用測向測時差的定位方法僅需兩個探測站即可完成云閃的空間三維定位，并且定位的站數越多，定位精度越高[7]。在設定4個探測站的基礎上研究云閃的定位算法、定位精度及最優(yōu)布站方式。

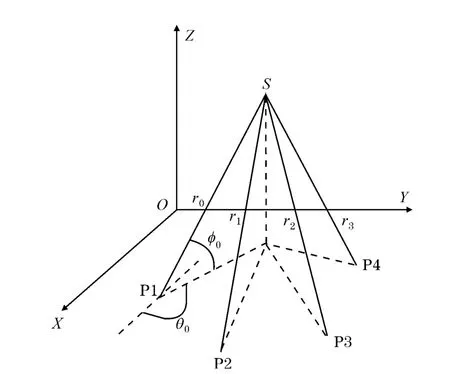
圖1 云閃輻射源與探測站位置關系

如圖1，建立4站云閃輻射源定位模型，4個地面探測站分為位于 P1、P2、P3、P4，站址坐標為 (xi，yi，zi)，i=0，1，2，3。P1為主站，P2、P3、P4為輔站。4個探測站的最大有效探測距離為200km，角度測量誤差小于3度，時間測量誤差小于50ns。主站及輔站均可測得云閃入射波的俯仰角、方位角和到達時間，為(θi，φi，ti)，i=0，1，2，3。由此可以確定主站和輻射源距離與各輔站和輻射源距離之差為Δri=c(t0-ti)，i=1，2，3。c為雷電電磁波傳播速度，其值為2.99792×10sm/s。再選用主站測得的方向信息則可以確定5個測量參數(φ0，θ0，Δr1，Δr2，Δr3)用以確定云閃發(fā)生位置。

根據圖1所示的閃電輻射源與各探測站的位置關系，結合主站測得的方位角和俯仰角以及云閃輻射脈沖到達各探測站的時間，可以得出定位方程:

式(1)中 ri= [(x-xi)2+(y-yi)2+(z-zi)2]1/2，i=0，1，2，3 。把 r0看作一個待求未知量，并將方程組(1)中各式化簡變形并整理成矩陣形式得:

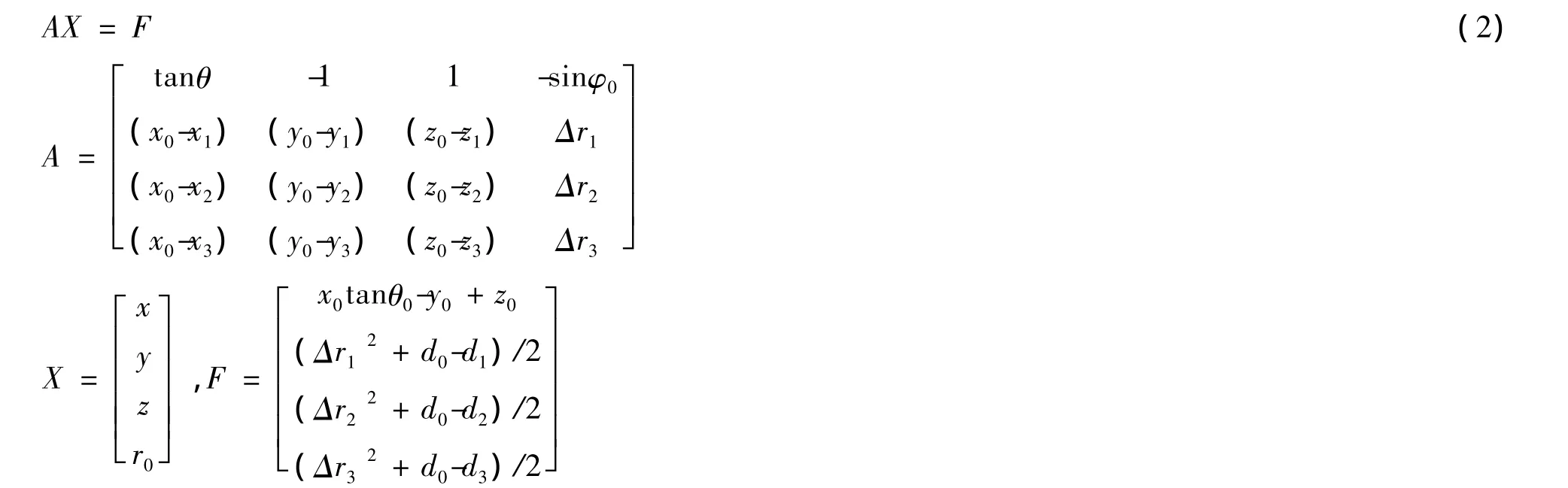
其中，di=x2i+y2i+z2i，i=0，1，2，3

式(2)成立的條件是rank(A)=4[8]。則此時，可求得云閃輻射源的空間位置:

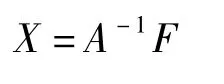
2 定位精度分析

云閃定位屬于無源定位，利用測向測時差法進行定位時，先忽略計算有關誤差和雷電信號提取有關誤差因素的影響，進而對定位誤差進行分析[9]。則云閃定位精度主要受到到達時間測量誤差、角度(俯仰角、方位角)測量誤差、站址測量誤差和探測站的布站方式的影響。

為了減小測時誤差對定位精度的影響，需要各探測站保持高精度的時間同步。隨著衛(wèi)星GPS同步授時技術的發(fā)展，閃電定位系統(tǒng)多運用GPS時鐘以解決各探測站的時間同步問題。對各探測站間的同步時間差在經過一定的修正之后誤差可保持在20ns之內，可以滿足云閃定位系統(tǒng)對時間同步的要求[10－11]。探測站獲取的方位角和俯仰角誤差主要來源于探測站的解算誤差。

想要獲得更高的閃電定位精度，探測站的合理布局優(yōu)化顯得尤為關鍵。為了描述定位精度與探測站幾何位置的關系，引入幾何稀釋精度(Geometric Dilution of Precision，GDOP)，是衡量系統(tǒng)定位精度的一個重要系數，定義為系統(tǒng)的定位誤差與測量距離的比率，反映實際的定位誤差對測量誤差的放大程度[11]。GDOP的表達式為:

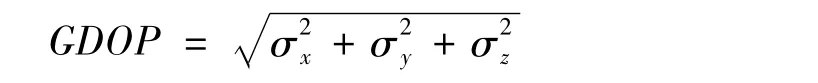
上式中，σx、σy、σz分別表示閃電輻射脈沖在x、y、z方向上的定位標準差，GDOP值越大，定位精度越低;GDOP值越小，則定位精度越高[12]。

對方程組(1)中各式求微分得，整理為矢量形式為:

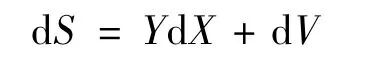
上式中，dS= [dθ0，dφ0，dΔr1，dΔr2，dΔr3]T表示主站測角誤差以及主站和各輔站到達時間差引起的誤差，dX=[dx，dy，dz]T表示云閃輻射源的定位誤差，dV= [kθ0，kφ0，k0-k1，k0-k2，k0-k3]T表示各探測站站址測量引入的誤差[13]。系數矩陣

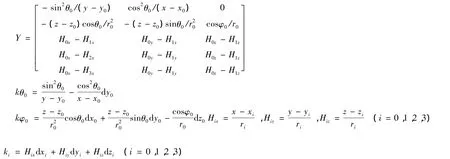
則可解出定位誤差dX的最小二乘解:

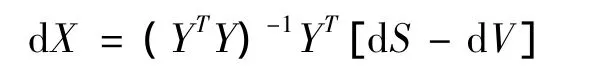
假設各探測站相互獨立，各探測站的探測量和站址誤差互不相關。σΔri(i=1，2，3)為各探測站因測時引起的距離誤差標準差，σθ、σφ分別為主站測得的方位角φ、俯仰角θ的誤差標準差，各探測站站址誤差標準差均為σs，且經過系統(tǒng)修正后，σΔri、σθ、σφ、σs均服從正態(tài)分布。設定時間差距離誤差標準差均為σΔ。則定位誤差協(xié)方差矩陣為:

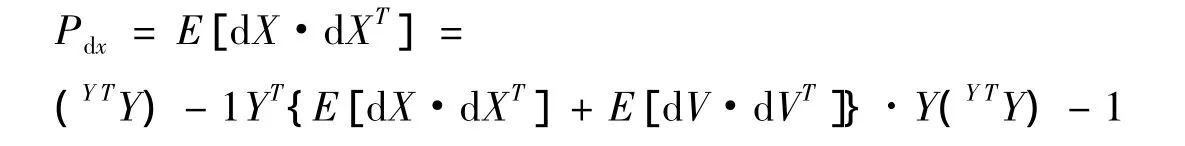
上式中:

3 不同布站方式仿真分析

云閃輻射信號的最大傳播距離為100～200km，因此云閃定位系統(tǒng)中的探測站的基線長度應小于200km[14]。根據誤差分析可知，云閃定位精度與測量誤差、站址誤差、布站方式等因素有關。顯然，測量誤差與站址誤差越小，閃電定位精度越高。在測量誤差和站址誤差一定的前提下，布站方式對閃電定位精度起到了重要作用。

常用的布站方式有正方形、菱形、T形和Y形等，不同布站方式下的定位精度分布各有特點。不同布站方式下各站坐標見表1。經過計算機Matlab仿真，圖1給了出基線長度為100km、輻射源高度為10km、測角精度為0.5°、測時精度為20ns時4種布站方式下的GDOP等高線圖，GDOP等高線單位為km。

表1 不同布站方式下各站坐標

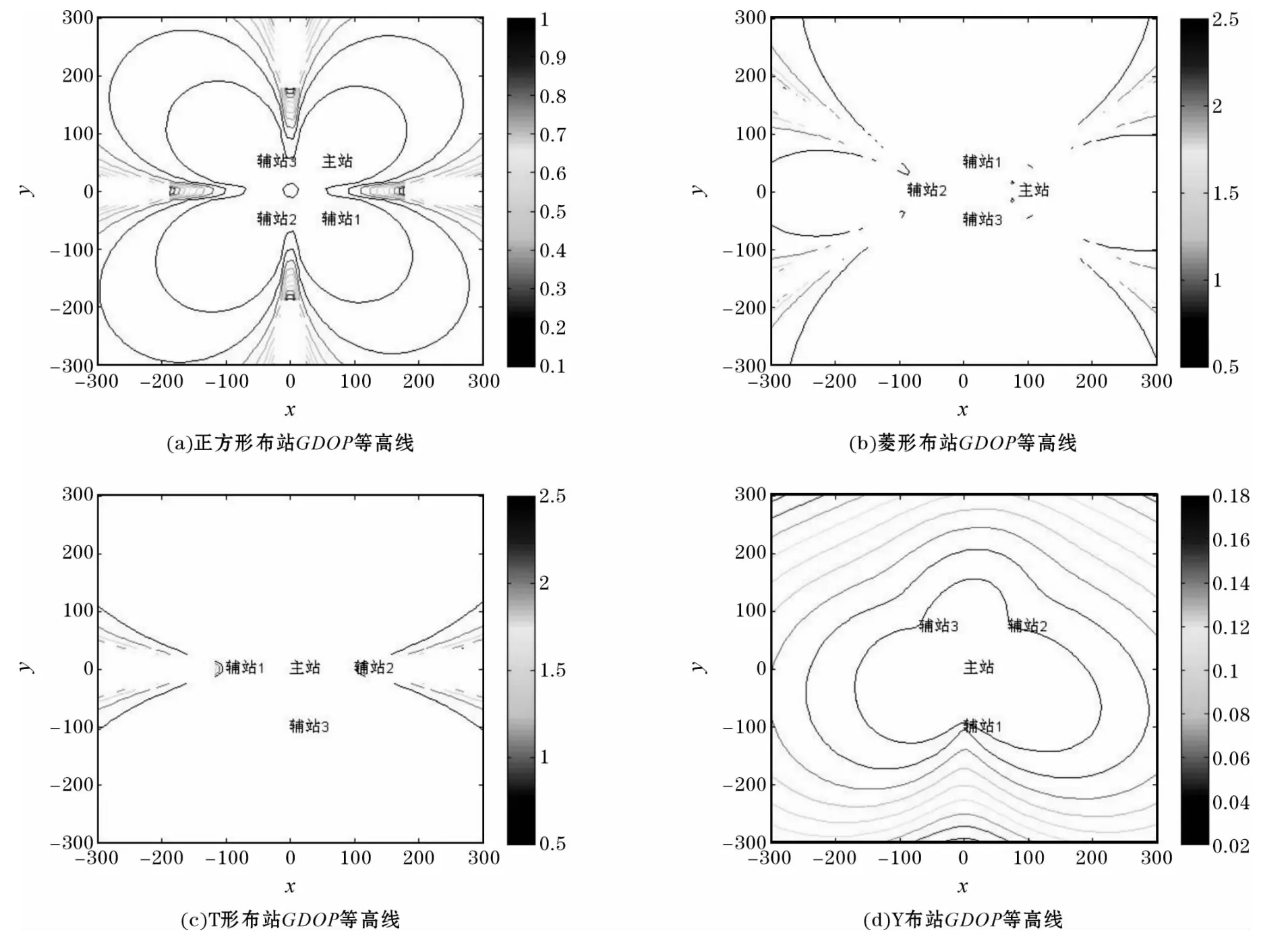
圖2 正方形、菱形、T形、Y形布站方式的GDOP等高線圖

由圖2可以看出，Y形布站的定位精度明顯優(yōu)于其他3種布站方式，且在整個定位區(qū)域內的定位精度分布較均勻，適合對于大區(qū)域內的全方位定位。除Y形外其他布站方式定位誤差圖像均呈左右對稱分布。正方形布站在兩條對角線方向上的定位精度高于菱形和T形，但其他方向的定位精度偏低。菱形布站定位精度在布站菱形外接矩形對角線方向上存在著模糊區(qū)，并且距離越長，模糊區(qū)張角越大，定位精度越低。T形布站定位精度分布在主站前后精度很高，但在左右方向上的精度較低并且隨著距離拉長模糊區(qū)增大。

若定位目標大致方向已知，菱形和T形布站因其定位精度分布的強方向性可作為布站的最優(yōu)選擇方式，但云閃定位屬于無源定位，使用Y形布站可以在較大區(qū)域內得到更均勻的定位結果，是更理想的布站方式。

4 定位精度影響因素分析

由以上分析可知，Y形布站在整個定位區(qū)域內的定位精度分布較均勻，是閃電定位系統(tǒng)的理想布站方式。那么在Y形布站前提下，主站位置、基線長度和主站與輔站相對高度這些因素又會對定位精度產生何種影響，下面進行詳細分析。

4.1 主站位置的影響

4個探測站坐標不變，改變主站位置，仿真數據如表2所示。經仿真，得到一組以原點為中心的Y形布站GDOP等高線圖，如圖3所示。

表2 主站位于不同位置時各站坐標

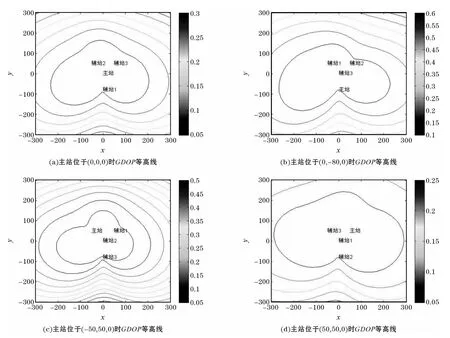
圖3 主站位于Y形不同位置的GDOP等高線圖

由仿真結果可以看出:當4個探測站坐標不變，改變主站位置時，GDOP等高線的形狀與數值隨主站位置不同而發(fā)生變化。與主站位于中心位置相比，主站位于Y形布站上方兩頂點時，相同距離GDOP等高線數值變小，則定位精度提高;主站位于Y形布站下方頂點時，相同距離GDOP等高線數值變大，則定位精度降低。

4.2 主站高度的影響

各輔站坐標不變，僅改變主站高度，仿真數據如表3所示。經仿真，得到一組Y形布站GDOP等高線圖，如圖5所示。

表3 主站位于不同高度時各站坐標

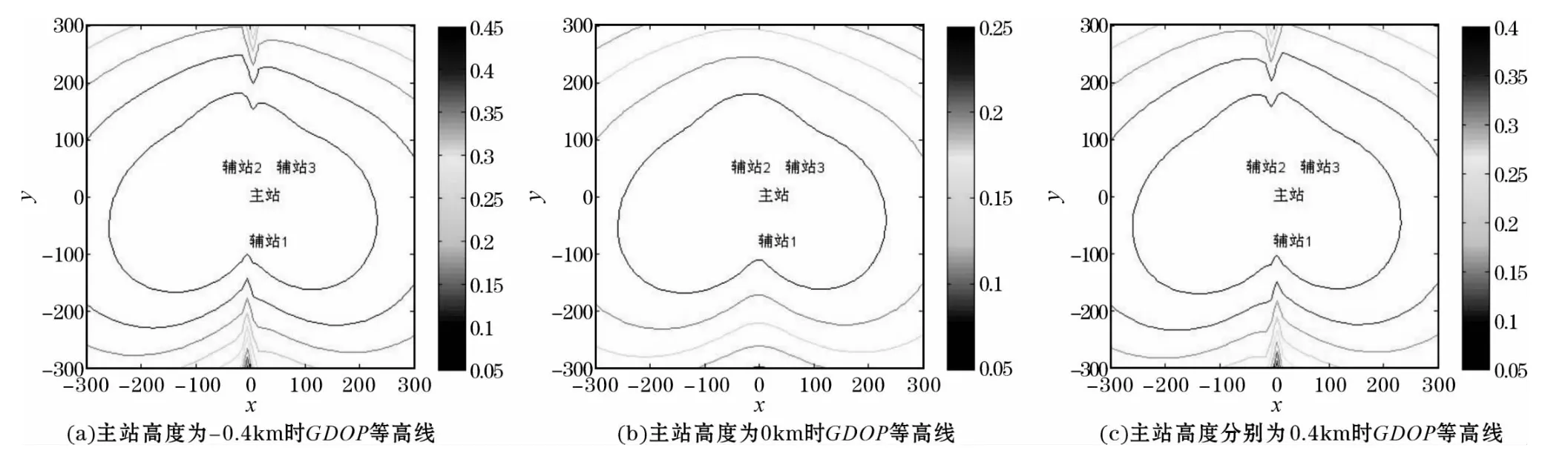
圖4 主站高度分別為－0.4km、0km、0.4km時GDOP等高線圖

由仿真結果可以看出:無論是主站高于輔站還是低于輔站，相同距離的GDOP等高線數值變化不大，但隨著主站與輔站高度差的增加，都會使主站前后方的定位精度降低。

4.3 基線長度的影響

主站位置不變，僅改變基線長度，仿真數據如表3所示。經仿真，得到一組Y形布站GDOP等高線圖，如圖4所示。

表4 不同基線長度時各站坐標

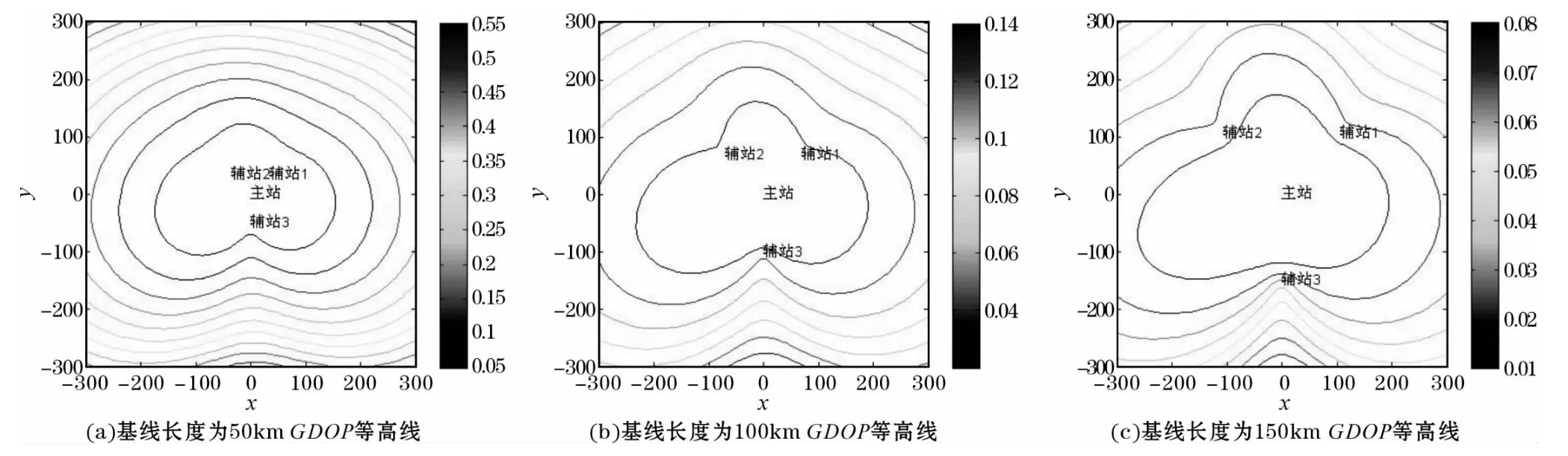
圖5 基線長度為50km、100km和150km時的GDOP等高線圖

由仿真結果可以看出:隨著基線長度的增加，相同距離GDOP等高線的數值變小，則定位精度提高。

5 結束語

在建立4站云閃定位模型的基礎上，詳細介紹了利用測向測時差無源定位法進行云閃定位的原理及算法。在探測精度及站址誤差一定的前提下，利用Matlab仿真，得出了4站探測網在4種幾何布站方式下的定位精度分布情況。通過對比分析，Y形布站方式是云閃定位理想布站方式，能夠在整個探測區(qū)域內得到更高的定位精度且分布均勻。

對于Y形布站，在探測范圍內增加基線長度可以提高定位精度。主站位置影響定位精度，當主站位于Y形上當兩頂點時，定位精度比主站位于其他頂點更高;無論主站高度高于輔站或低于輔站，拉長主站與輔站的高度差都會使定位精度在一定方向出現模糊區(qū)，降低定位精度。仿真得出的結論可以有效的對實際云閃4站探測網的布站優(yōu)化給予指導，為探測網的布站方式提供理論支撐。探測站測量誤差和站址誤差為云閃定位的影響在文中沒有進行闡述，這將是下一步的研究重點。

[1] 郄秀書，張義軍，張其林，等.閃電放電特征和雷暴電荷結構研究[J].氣象學報，2005，63(5):646.

[2] 田芳.江蘇省閃電定位儀觀測資料的修訂與分析[D].南京:南京信息工程大學，2009.

[3] Uman M A.The Lightning Discharge[M].New York:Academic Press，1987.

[4] 李云敏，孫秀斌，楊崧令，等.云閃定位算法及誤差分析[J].電子測量與儀器學報，2012，26(10):917.

[5] K.Becker.An Efficient Method of Passive Emitter Location[J].IEEE Transactions on Aerospace and Electronic Systems.1992，28(4):1091－1104.

[6] 孫仲康，周一宇，何黎星.單站基地有源無源定位技術[M].北京:國防工業(yè)出版社，1996:115－130.

[7] 張政超，童力.四站時差無源定位精度分析[J].中國電子科學研究院學報，2010，5(6):582.

[8] 陳玲，李少洪.無源測向測時差定位算法研究[J].電子與信息學報，2003，25(6):771－772.

[9] 張萍，趙文光，胡志祥，等.雷電定位系統(tǒng)云閃定位精度圖形因素分析[J].武漢大學學報(理學版)，2009，55(2):249.

[10] 張義軍，孟青，馬明，等.閃電探測技術發(fā)展和資料應用[J].應用氣象學報，2006，17(25):613－614.

[11] Krehbiel P，Thomas R，Rison W，et al.Lightning mapping observations in central Oklahoma[J].EOS，2000:21－25.

[12] 黃亞萍.基于TDOA和TOA的無線定位技術研究[D].南京:南京郵電大學，2012.

[13] 敖偉，張揚.基于Chan算法的無源雷達定位精度分析[J].電腦知識與技術，2009，5(10):2758－2759.

[14] 徐振魯.時差法多站無源定位及其信號處理技術研究[D].南京:南京航空航天大學，2010.

[15] 李京校.基于SAFIR資料的北京及周邊地區(qū)閃電特征分析[D].南京:南京信息工程大學，2011.

致謝:感謝成都信息工程學院中青年學術帶頭人科研基金(J201204)對本文的資助