加入信道估計誤差的MIMO雙向中繼最大和速率的研究*

盧雅哲，陳 宇，劉 璐，束 鋒，2*

(1.南京理工大學電子工程與光電技術學院，南京210094;2.東南大學移動通信國家重點實驗室，南京210096)

因為無線中繼傳輸系統可以拓寬覆蓋范圍和提高系統容量，所以是一個有前景的研究課題。文獻［1-3］都是研究分析中繼系統容量的文章。為了提高中繼網絡的容量，我們需要考慮點對點多天線輸入多天線輸出(MIMO)的情況［4］。MIMO中繼系統的容量在文獻［5］中有研究。大部分中繼系統都是假設工作在半雙工情況下的，也就是中繼不同時接受和發送信息，這樣可以避免中繼節點的環路干擾。

文獻［6-7］中通過研究雙向中繼協議來克服半雙工頻譜效率損失。在第一個時隙，兩個源節點同時發送信息給中繼;在第二個時隙，中繼節點傳輸先前的信號給用戶終端。因為每個終端節點都知道其自身的信道狀態信息，所以在終端節點可以消除自身的干擾［7］。相比于需要四個時隙傳輸信號的單向中繼協議來說，雙向中繼協議只需要兩個時隙。所以，雙向中繼協議可以從半雙工中繼信號中補償一大部分的容量損耗。因此雙向中繼是目前研究的熱點。

在實際中繼系統中，因為放大轉發AF(Amplify and Forward)方式中繼節點只需要線性處理基帶信號，不需要解碼信號，所以它相比于解碼轉發方式易于實現而且有著較低的計算復雜度。文獻［8］研究了一個基于奇異值分解SVD(Singular Value Decomposition)的線性方法去實現MIMO AF單向中繼系統的系統容量。對于雙向中繼而言，迫零ZF(Zero Forcing)和最小均方誤差 MMSE(Minimum Mean Square Error)算法在文獻［9］中都有所研究。文獻［10］研究用戶單天線中繼多天線的AF雙向中繼系統，文中利用迭代算法計算基于最大和速率的權值矩陣。文獻［11］研究用戶和中繼都是多天線的MIMO AF雙向中繼系統，文中利用梯度下降法迭代運算得出最優權值矩陣F。

本文在文獻［11］的基礎上引入了信道估計誤差，在非理想的狀態下推導出更一般的最優權值矩陣F的計算公式，這是本文的一大創新點。計算系統和速率和相應的誤碼性能，對比不同估計誤差下的通信性能，結合通信系統對性能的要求得出我們在進行信道估計中需要滿足的精度。

在本文中(·)T、(·)H分布表示矩陣的轉置和共軛轉置，(·)*表示矩陣的共軛。ε表示期望，IN表示N×N的單位矩陣，tr(A)表示矩陣的跡，|A|表示矩陣的行列式。

1 系統基本模型

假定MIMO雙向中繼系統中用戶有M根天線中繼有N根天線如圖1所示。兩個用戶通過一個中繼相互通信，并且工作在時分雙工模式。本文我們假設兩個用戶節點可以直接通信忽略大尺度衰落。

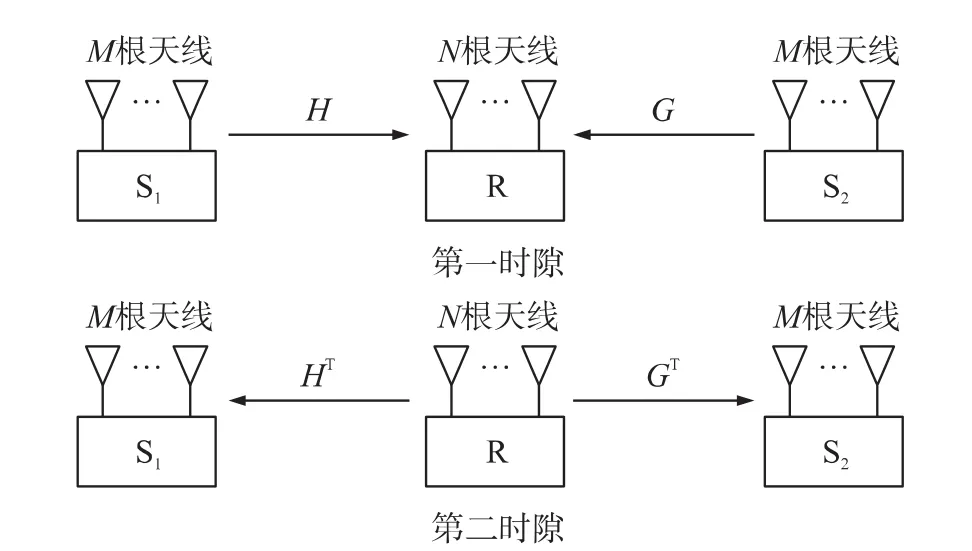
圖1 系統信道模型

我們需要為信道估計誤差建模，在本文中，我們引入文獻［12］定義的Gauss-Markov模型。

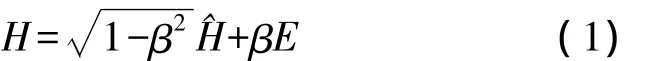
其中H是真實信道，H^是估計信道，噪聲E服從零均值單位方差高斯隨機分布。標量β表征了節點對信道信息的了解情況。當β=0時，意味著知道完美的CSI，估計信道等于實際信道，當β=1時意味著完全不知道信道信息。這是兩種極端的情況，實際的信道估計在這兩種情況之間。

在第一個時隙，兩個終端節點同時把它們的信號sA和sB傳送給中繼節點R。然后接收到的N維信號向量r為:

其中H和G是從終端S1和S2到中繼端的N×M維信道矩陣，n是零均值復高斯隨機噪聲ε(nn+)=IN，sA和sB是M維傳輸信號向量其中PA和PB是終端S1和S2的功率。

在第二個時隙，中繼端進行線性處理乘以權值矩陣F。那么中繼節點要傳輸的信號向量x為:

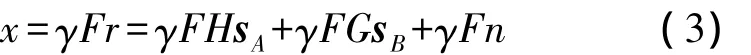
其中 γ是功率規格化系數，滿足功率約束條件ε{tr(xx+)}=PR，可以表示為:

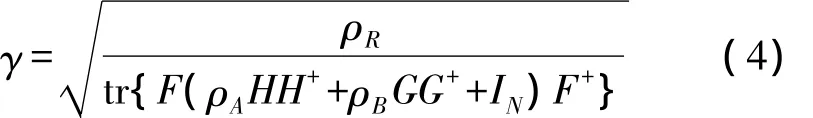
中繼端處理過后的信號x從中繼節點傳輸到終端節點S1、S2，如圖1所示，廣播信道矩陣為HT和GT，所以在兩個終端節點接收到的信號yA和yB可以表示為:

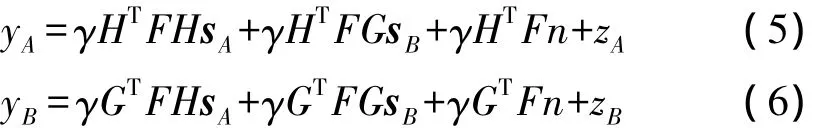
其中zA和zB是協方差矩陣為IM的復高斯白噪聲。

因為在終端節點我們知道所估計的信道，但是由于信道存在估計誤差，所以自干擾不可以完全消掉。自干擾項減去估計的信道，我們可以得到最終終端節點和為:

從式中我們可以得出雙向中繼的性能取決于權值矩陣F。下面一節我們將要計算一個滿足和速率最大化的權值矩陣F。

2 最大化和速率

假設在式(7)、式(8)信號的總噪聲是零均值圓周對稱的復高斯分布，則MIMO雙向中繼系統的和速率可以表示為:

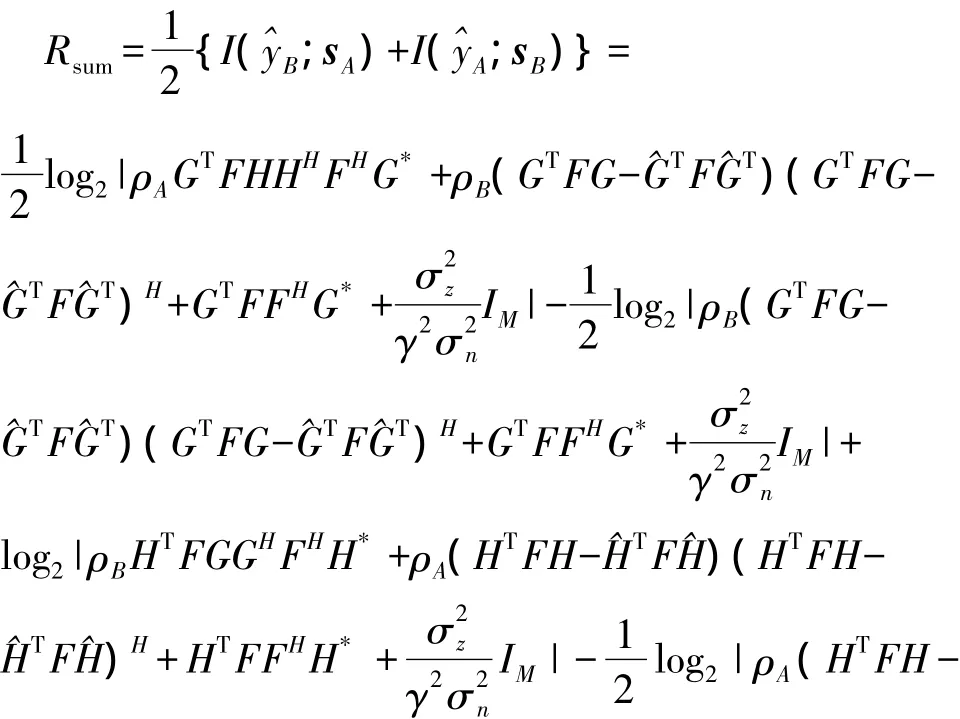
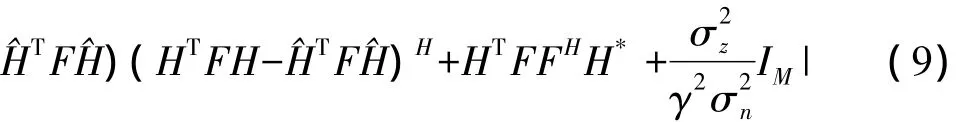
其中I(x;y)表示x和y的互信息量，因為它們工作在半雙工的模式下，所以要乘以系數1/2，γ是由式(4)給出的值。

接下來，為了找到使得和速率最大的最優中繼權值矩陣F，我們把問題描述成為:

因為函數Rsum不是關于F的一般凸函數或凹函數，所以它的最大化問題難以分析和解決。在本文中我們引入文獻［11］所提出的梯度下降算法來解決式(10)最優化問題。

因為和速率Rsum是一個實函數，所以我們可以認為為了計算簡便，我們設:

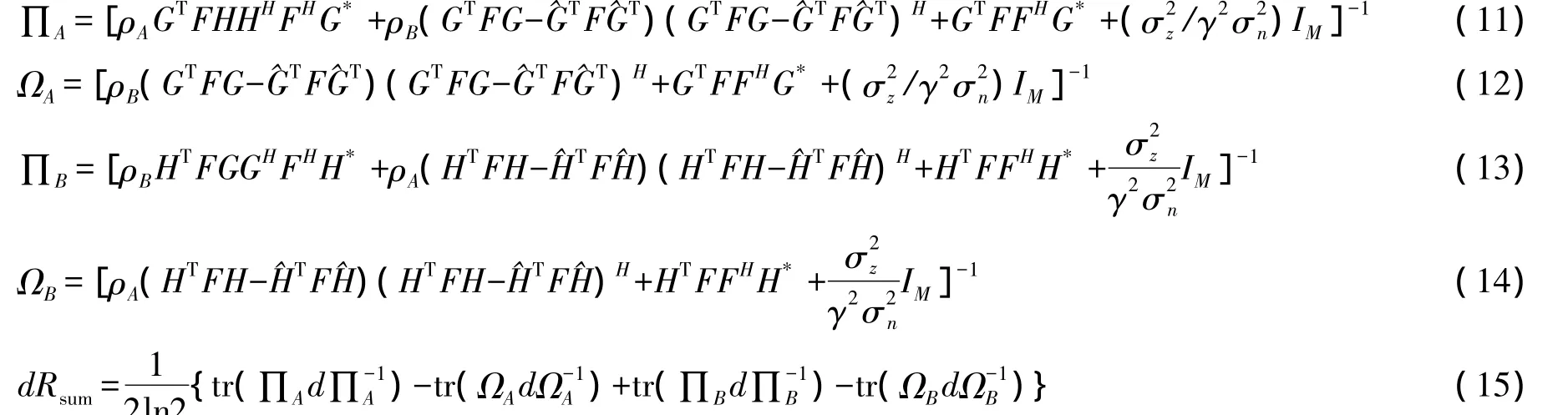
速率和的微分式(9)可以寫為式(15)。在這里我們考慮了 γ也是 F的函數。這個結果可以用公式［?tr(AXX+B)］/?X+=BAX來證明。那么和速率的梯度可以表示成為:

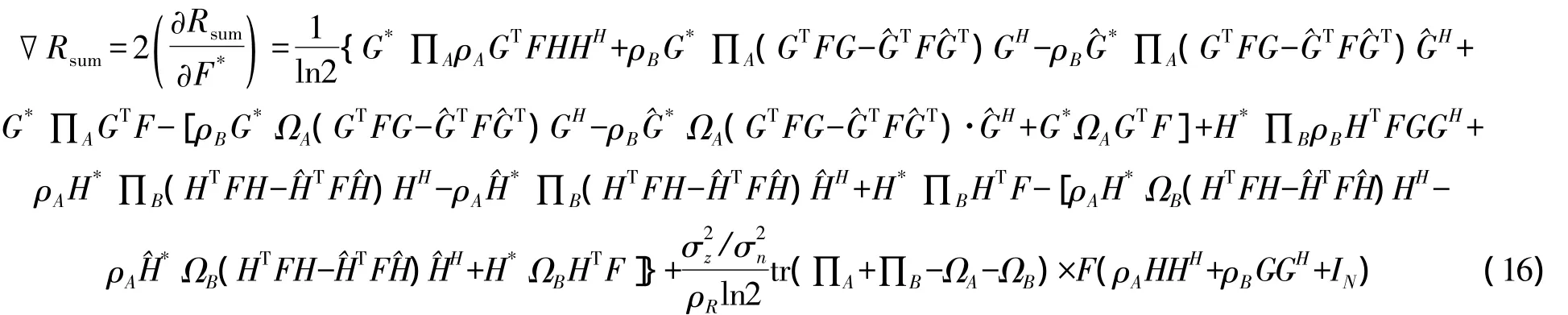
得出梯度公式，我們運用迭代算法解決式(16)問題

在這個迭代過程中，ε是終止容忍值。文獻［13］中給出了一些確定步長的線性搜索方法。我們采用Armijio’s Rule方法搜索步長，則步長δ可以表示為δ=vm，其中m是滿足下面式子的最小整數

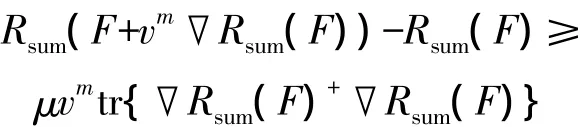
在這里v和μ是0到1范圍內的一個確定的值。

因為該問題是一個非凸問題，所以迭代算法并不能保證全局最優，所以我們為了保證得到的矩陣最優，就要產生多個初始值多次迭代，然后從所得的結果中選出最優值。

3 仿真結果

在這個部分我們要仿真不同信道誤差估計下的最大和速率和誤碼性能。在仿真中我們設PA=PB=P/4，，其中P是中繼網絡的功率。SNR=P/，其中H和G的元素是獨立同分布的零均值單位方差復高斯信道。我們在仿真中初始化F權值矩陣10次以得到全局最優。

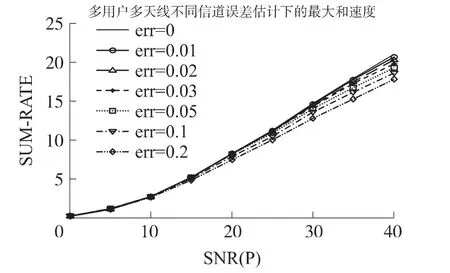
圖2 不同估計誤差下的最大和速率

在圖2中，我們選擇β的取值分別為0、0.01、0.02、0.03、0.05、0.1、0.2;選擇用戶天線個數M=2，中繼天線個數N=4，噪聲的方差==1，為了使得到的最優值為全局最優，我們設置20個初始值來計算并從中選擇最優值。從圖2中可以得出，隨著信道估計誤差的增大最大和速率均勻下降，所以我們要保證一定的信道估計誤差來保障和速率。

在圖3中，我們選擇β的取值分別為0、0.01、0.02、0.05、0.1;天線數目和噪聲與上面相同，從圖3中可以得出，隨著信道估計誤差的增大誤碼性能隨之下降，尤其在高信噪比的情況下下降更多，我們可以看出，當信道估計誤差超過0.05的時候系統的誤碼性能就會變得非常差，所以我們要保證一定的信道估計誤差不能超過這一值。

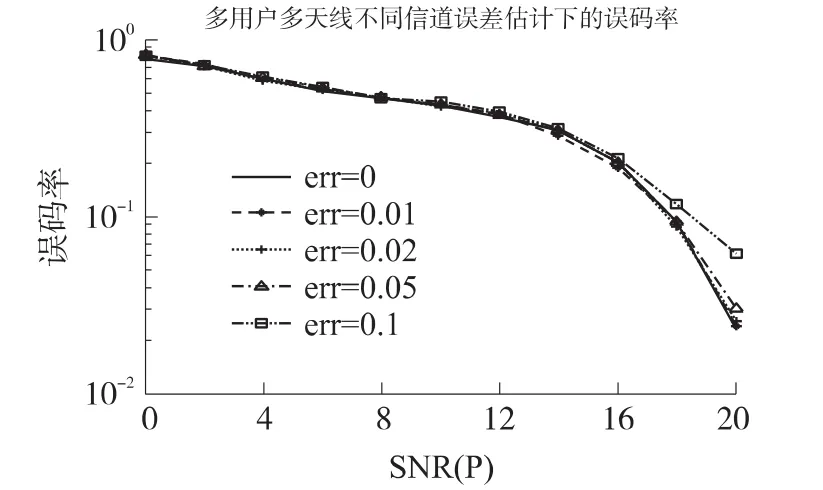
圖3 不同信道估計

4 總結

在這篇文章里，我們研究了加入信道估計誤差的最大和速率問題。我們運用了梯度迭代法計算波束成形矩陣F，對比了不同信道估計誤差下的最大和速率和誤碼性能，得出在該算法下為了保證通信質量必須控制信道估計的誤差不能太大。由于現實中，信道估計不可能完全沒有誤差，所以這個研究具有很強的現實意義，也是目前國內外學者的一個研究熱點。

［1］Cover T M，El Gamal A A.Capacity Theorems for the Relay Channels［J］.IEEE Trans Inform，1979，25(5):572-584.

［2］Gastpar M，Vetterli M.On the Capacity of Wireless Networks:The Relay Case［J］.Proc IEEE Infocom，2002(3):1577-1586.

［3］Kramer G，Gastpar M，Guptar P.Capacity Theorems for Wireless Relay Channels［J］.Allerton Conf Comm，Control and Comput，2003:1074-1083.

［4］Wang B，Zhang J，Host-Madsen A.On the Capacity of MIMO Relay Channels［J］.IEEE Trans Inform Theory，2005，51(1):29-43.

［5］Bolcskei H，Nabar R U，Oyman O，et al.Capacity Scaling Laws in MIMO Relay Networks［J］.IEEE Trans Wireless Comm，2006，5(6):1433-1444.

［6］Rankov B，Wittneben A.Spectral Efficient Signaling for Half-Duplex Relay Channels［C］//Proc IEEE Asilomar Conf on Signals，Systems and Comput，2005.

［7］Rankov B，Wittneben A.Spectral Efficient Protocols for Half-Duplex Fading Relay Channels［J］.IEEE J Select Areas Comm，2007，25(2):379-389.

［8］Tang X，Hua Y.Optimal Design of Non-Regenerative MIMO Wireless Relays［J］.IEEE Trans Wireless Comm，2007，6(4):1398-1407.

［9］Unger T，Klein A.On the Performance of Two-Way Relaying with Multiple-Antenna Relay Stations［J］.IST Mobile and Wireless Comm Summit Budapest，2007.

［10］Namyoon Lee，Hyun Jong Yang.Achievable Sum-Rate Maximizing AF Relay Beamforming Scheme in Two-Way Relay Channels［C］//ICC Workshops’08.IEEE，Beijing，2008.19-23.

［11］Lee Kyoung-Jae，Lee Kwang Won，Sung Hakjea.Sum-Rate Maximization for Two-Way MIMO Amplify and Forward Relaying Systems［C］//Vehicular Technology Conference，IEEE 69th，Barcelona，26-29 April 2009.

［12］Wang C，Au E K S，Murch R D，et al.On the Performance of the MIMO Zero-Forcing Receiverin the Presence ofChannel Estimation Error［J］.IEEE Trans Wireless Commun，2007，6(3):805-810.

［13］Bazaraa M S，Sherali H D，Shetty C M.Nonlinear Programming:Theory and Algorithms［M］.3rd Ed.New York:John Wiley and Sons，2006.