小脈沖約束下的近圓軌道控制方法研究

黃美麗 羅渠 趙峭

（北京空間飛行器總體設計部，北京 100094）

1 引言

大部分的應用衛星都是近圓軌道衛星，其中又有很多是需要進行軌道控制的。以選用凍結軌道的遙感衛星為例［1-4］，為避免衛星入軌之后進行減速機動，一般入軌時的初始軌道高度相對目標軌道高度有30km左右的負偏置，入軌之后需要由衛星利用自身的推力器進行變軌，將軌道抬升至目標軌道。特殊情況下，初始軌道高度的負偏置量還有可能大于30km，例如我國的海洋二號（HY-2）衛星［5］，初始軌道高度的負偏置量為60km 左右。軌道半長軸a、偏心率e、近地點幅角ω三個參數的調整可以稱為軌道平面內參數的調整，偏心率及近地點幅角（統稱為偏心率矢量）的調整是通過橫向脈沖（即在軌道平面內垂直于矢徑，沿衛星運行方向）在調整半長軸的同時來完成的。對于半長軸負偏置量大于30km 的軌道，一般來說，調整偏心率矢量所需的半長軸調整量小于半長軸的偏置量。近圓軌道的控制根據控制前后平面內參數（半長軸、偏心率、近地點幅角）的要求，只需要兩個橫向脈沖速度增量就可以完成，在工程實現時一般根據總控制量、單次控制時長約束以及控制精度要求，將兩個橫向脈沖拆分為若干批次的雙脈沖控制來完成。

采用傳統的雙脈沖控制方法［6-8］，則一條軌道圈內至多只能進行兩次軌道控制，在單次控制小脈沖約束下，單次控制量很小，若軌道調整量大，則總控制次數很多，整個控制周期很長。本文針對這一問題，提出了一種單次控制小脈沖約束下的近圓軌道平面內參數控制方法，增加在一條軌道圈內的軌道控制次數，可達到大幅縮短整個軌道控制周期的目的，保證在完成提升軌道高度的同時，完成偏心率及近地點幅角的調整。

2 雙脈沖近圓軌道平面內參數控制方法

對近圓軌道控制一般采用簡化的近似解析解，這種方法也是國際通用的，我國資源衛星（ZY）的軌道控制也成功地采用了這種方法。根據文獻［6］，令ex＝ecosω，ey＝esinω，Δa、Δex、Δey分別為a、ex、ey的總控制量。調整偏心率矢量所需的半長軸調整量Δae為

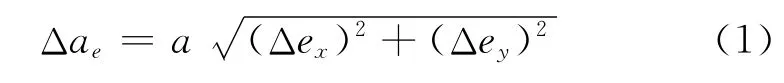
只需要兩個橫向脈沖速度增量就可以同時實現三個參數的調整。若恰當安排這兩個脈沖的位置和大小，還可以使總的速度增量達到最小。具體來說可以根據Δa以及Δae的大小分為2種情況：

1）Δa＞Δae

這種情況下，第一個速度增量的位置u1可以任選，位置選定后速度增量的大小ΔV1以及第二個速度增量的位置u2和大小ΔV2便都完全確定，而且兩個速度增量是同向的：

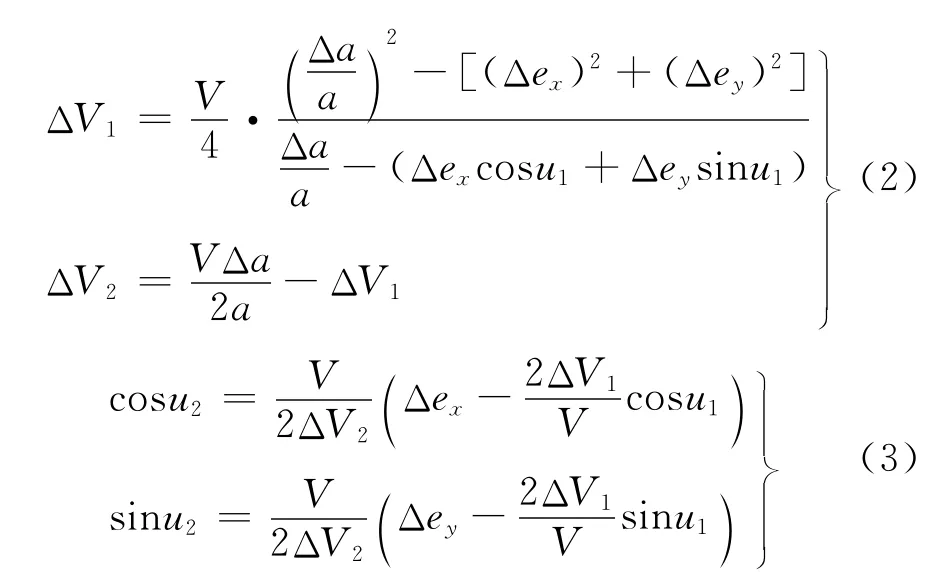
式中：V為軌道速度。

2）Δa≤Δae

雌飛魚會小心翼翼地將魚卵產在棕櫚葉的葉柄上，它們的卵又輕又小，卵的表面有許多絲狀突起物，這些呈絲狀且有一定黏性的突起物可以把飛魚卵牢牢地纏在棕櫚葉上。

這種情況下，兩次機動的位置和速度增量的大小都是完全確定的，但速度增量的方向相反，位置正好相差180°：

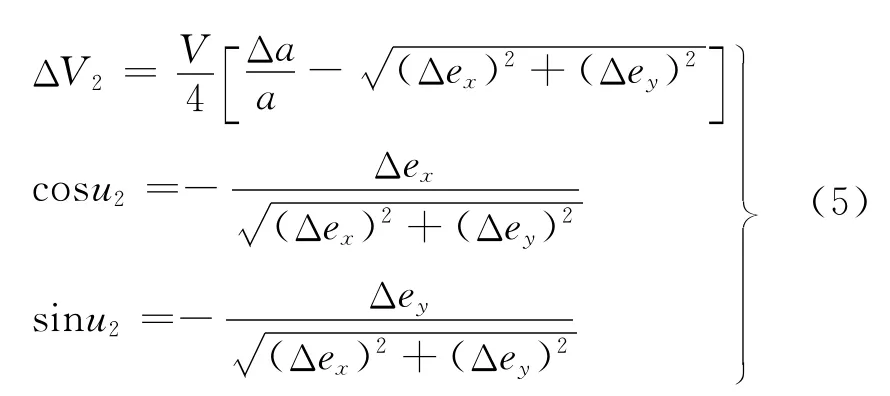
上述兩種情況中，兩次機動的順序都是可以交換的。

在實際工程應用中，一般選擇將這兩個脈沖分成若干個批次的雙脈沖來進行控制，每組機動控制施加的速度增量位置不變，僅對速度增量的大小分批次進行，機動次數根據總控制量、單次控制時長約束以及控制精度要求綜合確定。

3 小脈沖約束下的近圓軌道控制方法

雙脈沖近圓軌道平面內參數控制方法，由于機動位置約束，一條軌道圈內至多只能進行兩次機動控制，在單次控制小脈沖約束下，單次控制量很小，若軌道調整量大，則總控制次數很多，整個控制周期很長。

以海洋二號衛星為例，初始軌道高度的負偏置量為60km 左右，即衛星入軌后需要利用自身的推力器將軌道高度抬高60km 左右，才能進入正常的工作軌道。衛星入軌后，軌控推力器由于羽流擾動影響，在工作時會產生＋Z向偏航擾動力矩，受磁卸載能力的影響，每軌噴氣時間有限。以2個1N 的推力器同時點火為例，單次噴氣最長時間僅為10s左右。這種情況下，若采用一個軌道圈2次機動的方式，則需要機動上千次，完成整個軌道控制需要上百天的時間。因此，需要提高機動變軌頻率才有可能縮短多軌道控制時間。

3．1 控制原理和方法

對于我國的遙感衛星而言，一般星上安裝的軌控推力器都是沿衛星本體-X方向安裝的，正常對地姿態飛行的情況下，只能提供加速增量，要提供減速增量必須進行姿態180°機動。為了避免姿態機動，半長軸的入軌參數值一般都有偏置量，并且偏置量考慮了半長軸、偏心率以及近地點幅角的最大入軌誤差。

由于運載火箭的實際入軌精度一般遠遠優于入軌精度要求，因此，調整偏心率及近地點幅角所需的半長軸調整量一般小于半長軸偏置量，即Δa＞Δae。這種情況下，半長軸的總控制量大于調整偏心率矢量所需的半長軸調整量，因此，考慮將軌道平面內參數控制分為兩個階段：第一階段控制目標是抬高半長軸，但保證偏心率基本不變；第二階段是同時調整平面內參數半長軸、偏心率、以及近地點幅角。

這樣劃分的優點，在于要在偏心率基本不變的前提下達到抬高半長軸的目的，一條軌道圈內的軌道控制次數不局限于雙脈沖近圓軌道平面內參數控制方法的兩次，而是可以靈活地設置控制次數，從而達到增加一條軌道圈內軌道控制次數的目的。

（1）采取多點對稱點噴方式，在一條軌道圈內進行多次變軌，保證偏心率基本不變。

多點對稱點噴是指在一條軌道圈內均勻地進行多次小脈沖軌道機動控制，假定變軌次數為N（N為偶數），則相鄰兩次機動間的相位差為360°／N，即每隔1／N軌道圈進行一次機動。第一次機動的位置可以任選，N可以任選，脈寬根據變軌次數以及推力器點火時長約束確定。采取這種變軌方式，由于機動位置對稱，且脈寬相同，機動的效果是半長軸均勻地抬升，而偏心率基本不變。

以4脈沖對稱點噴為例，機動控制示意如圖1所示。

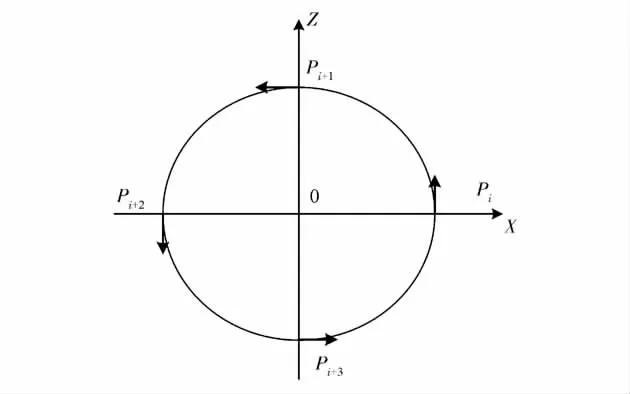
圖1 4脈沖對稱點噴的機動示意圖Fig．1 Drawing of 4-pulse maneuvering

多點對稱點噴的控制量Δa1為

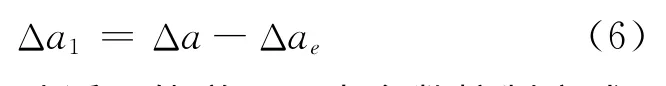
（2）采取雙脈沖近圓軌道平面內參數控制方式，在一條軌道圈內進行兩次變軌，在抬升軌道高度的同時，調整軌道偏心率及近地點幅角至目標值。

第二階段的控制方式按照3．2節給出的雙脈沖近圓軌道平面內參數控制方法進行控制，雙脈沖的控制量為Δae，控制量及控制位置根據式（2）～（5）計算，可以分成多個批次進行，在抬升軌道高度的同時將偏心率及近地點幅角調整到位，最終捕獲目標工作軌道。

3．2 算例

給定衛星初始軌道參數以及目標軌道參數見表1。

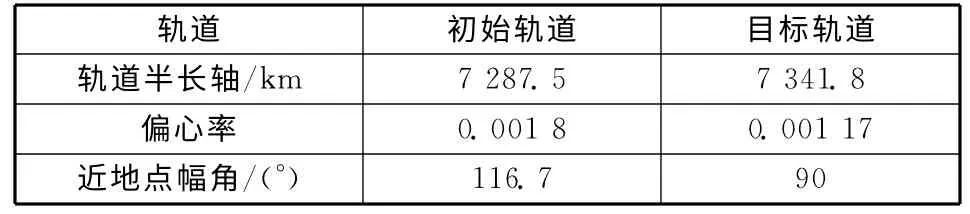
表1 主要軌道參數（平根）Table 1 Major Orbit Elements

根據表1計算得出，調整偏心率矢量所需的半長軸調整量Δae為6．75km，即第一階段軌道半長軸調整量為47．55km，第二階段軌道半長軸調整量為6．75km。

衛星在軌實際控制過程中，由于控制誤差的影響，實際控制結果不可能與理論脈沖計算結果完全一致，為避免第二階段的控制出現減速機動的情況，在第一階段控制預留1km 的余量，即第一階段軌道半長軸調整量為46．55km，第二階段軌道半長軸調整量為7．75km。

選取4個1N 推力器聯合進行變軌，每圈16脈沖機動控制，脈寬4s，將軌道半長軸抬高46．55km，通過商業STK 軟件進行仿真，第一階段偏心率及近地點幅角的變化情況如圖2～圖4所示。相比每圈2脈沖機動控制，16脈沖可以將控制周期縮短到1／8。

第一階段控制結束后，軌道參數：①半長軸為7 333．98km；②偏心率為0．001 929 410 8；③近地點幅角為108．667 949°。

對比初始軌道參數可以看出，偏心率變化很小，可以近似認為基本不變。

第二階段半長軸的控制量為7．75km，根據第二階段軌道參數的調整量關系分析可知，控制方法應采用雙脈沖近圓軌道平面內參數控制方法的第一種情況，第一個速度增量位置u1可以任選，考慮到實際情況中衛星在我國國境內時的相位位置為30°或150°附近，可以安排第一次脈沖控制在我國地面測控站弧段可見的范圍內實施，故選擇第一個速度增量位置u1＝30°。由式（1）～式（4）可得，雙脈沖控制的控制量及位置為：①第一個速度增量位置u1＝30°；②第一個速度增量大小ΔV1＝0．655 12m／s；③第二個速度增量位置u2＝301．835 5°；④第二個速度增量大小ΔV2＝3．240 09m／s。

針對上述計算結果，通過STK 商業軟件進行仿真，仿真結果表明，半長軸、偏心率及近地點幅角通過一組雙脈沖控制或分成若干個批次的雙脈沖控制可以同時達到目標值，實現目標軌道捕獲。

我國的海洋二號衛星，其軌控推力器每軌只能進行小脈沖軌道機動控制，按傳統的雙脈沖控制方法需要112d，采用了上述軌道控制方法，在14d進行了1578次軌道機動，完成了全部軌道調整，進入目標工作軌道，控制時間縮短了98d。

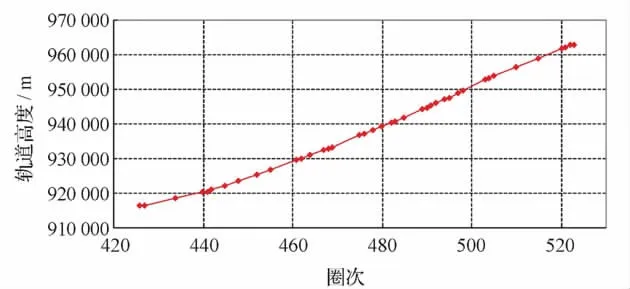
圖2 16脈沖對稱點噴的半長軸變化Fig．2 Variation of semi-major axis under 16pulses

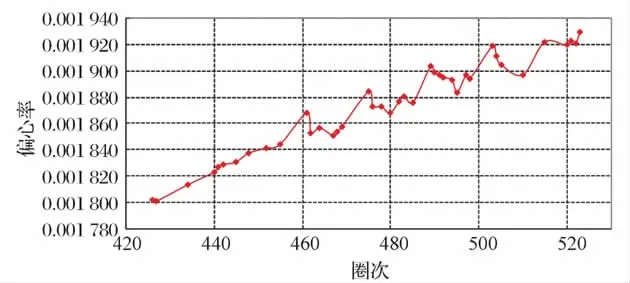
圖3 16脈沖對稱點噴的偏心率變化Fig．3 Variation of eccentricity under 16pulses

圖4 16脈沖對稱點噴的近地點幅角變化Fig．4 Variation of argument of perigee under 16pulses

4 結束語

本文提出的小脈沖約束下的近圓軌道平面內參數控制方法，通過多點對稱點噴以及雙脈沖控制兩階段軌道調整，可在第一階段多點對稱點噴控制環節增加一條軌道圈內的軌道控制次數，大幅縮短整個軌道控制周期，完成目標軌道捕獲。這種控制方法可以應用于軌道平面內參數調整量較大但單次點火時長限幅較小的衛星，使衛星在最短的時間內進入目標軌道，執行飛行任務。

（References）

［1］楊維廉．凍結軌道的一階解［J］．中國空間科學技術，2002，22（4）：45-50

Yang Weilian．A first order solution for frozen orbit［J］．Chinese Space Science and Technology，2002，22（4）：45-50（in Chinese）

［2］Brouwer D．Solution of the problem of artificial satellite theory without drag［J］．Astronautical Journal，1959，64：378-397

［3］楊維廉．基于Brouwer平根數的凍結軌道［J］．中國空間科學技術，1998，18（5）：13-18

Yang Weilian．Frozen orbit based on brouwer mean orbit elements［J］．Chinese Space Science and Technology，1998，18（5）：13-18（in Chinese）

［4］陳潔．太陽同步衛星的軌道設計［J］．上海航天，2004，21（3）：34-38

Chen Jie．Orbit design of Sun-synchronous satellite［J］．Aerospace Shanghai，2004，21（3）：34-38（in Chinese）

［5］王敏．海洋二號衛星工程創造五個“第一”［J］．中國軍轉民，2011（9）：78-79

Wang Min．The five‘First Times’created by HY-2project［J］．Defense Industry Coversion in China，2011（9）：78-79（in Chinese）

［6］楊維廉．近圓軌道控制的分析方法［J］．中國空間科學技術，2003，23（5）：1-5

Yang Weilian．An analytical method for controlling near circular orbits［J］．Chinese Space Science and Technology，2003，23（5）：1-5（in Chinese）

［7］肖業倫．航天器飛行動力學原理［M］．1版．北京：中國宇航出版社，1995

Xiao Yelun．Flight dynamics theory of spacecraft［M］．1st ed．Beijing：China Astronautics Press，1995（in Chinese）

［8］劉林．航天器軌道理論［M］．北京：國防工業出版社，2000

Liu Lin．Orbit theory of spacecraft［M］．Beijing：Nationa1Defense Industry Press，2000（in Chinese）