淺析龍門吊拉車皮對大車輪啃道及斷軸的危害

.南昌鐵路局龍巖工務段；.南昌鐵路局龍巖車務段 連慶勇 徐錦輝

龍巖東站貨場有一臺20／10t C型龍門起重機(以下簡稱門吊)，于1997 年9 月投入運用生產。主要承擔整車、零擔、集裝箱的裝卸作業。近年來，隨著我國經濟的不斷發展，鐵路運輸量不斷加大，龍巖東站貨物裝卸作業量也逐年增長。該機自投產以來，使用頻繁，已成為保證鐵路運輸暢通、加快貨物周轉不可缺少的設備。但由于操作人員違章作業，經常用門吊的索具（鋼絲繩）拉動貨車對位裝車，致使該設備近年經常出現大車啃道及車輪斷軸現象。

1 門吊拉車原因剖析

隨著鐵路貨物裝卸機械化的不斷發展，裝卸作業量逐年上升，機械作業逐漸代替了人力作業，一向以撬棍作為推車工具，臉朝鐵軌背朝天拼命推車的場面，在機械化程度高的地方，愈來愈少見，甚而見不到了。究其原因：一則少數職工依賴機械，貪圖省事的惰性心理和行為明顯增多；二則大多數職工搶裝搶卸提高經濟收入的意識大大增強；三則個別職工按章操作、愛護設備、延長設備壽命的觀念有所削弱；四則吊機發生故障，對作業班組（拉車）責任者考核不力，缺乏經濟制約有很大關系。

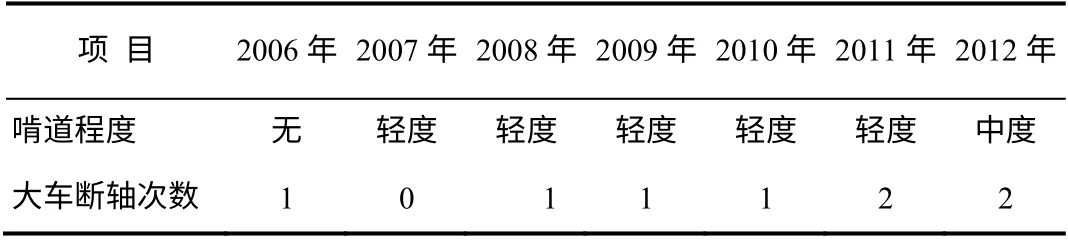
表1 2006 年～2012 龍巖東貨場20／10 tC型 門吊大車啃道、斷軸情況表

從表1 可以看出，大車啃道、斷軸自2006 年開始，幾乎每年都有發生，2011 年至2012 年發生的大車斷軸比以前增多一倍。其啃道程度也由原來的輕度，發展到中度。這是非正常狀況，無疑影響著設備的完好率、利用率和故障停機率。

2 門吊拉車造成大車啃道與斷軸分析

2.1 力學計算與分析（以主動車輪軸為研究對象）

2.1.1 走行梁拉車點A力學分析(見圖1、圖2)

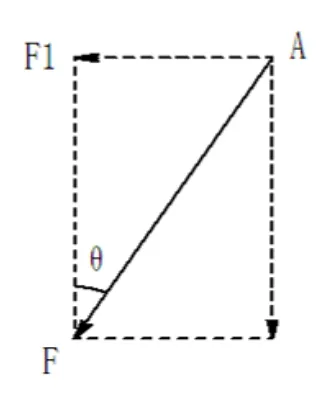
圖1

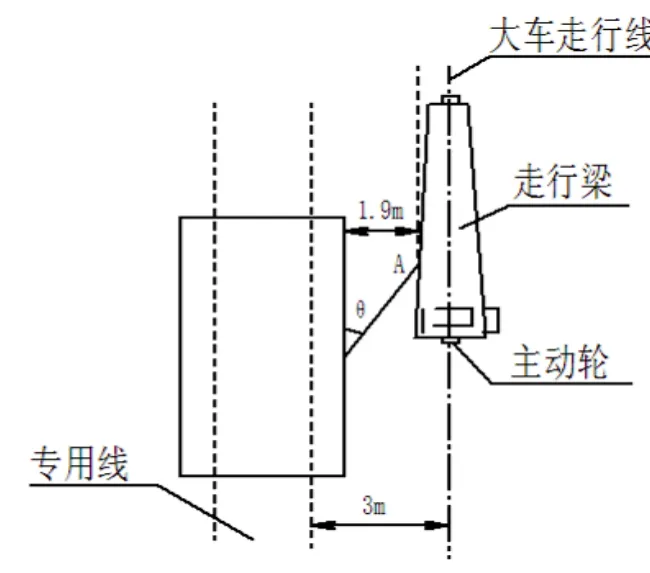
圖2

從圖1可知，以大車走行梁支點A上的拉車鋼絲繩與走行梁中心線成一夾角θ（θ 的大小與鋼絲繩長短成正比例關系）。

設鋼絲繩拉車的作用力為F（F跟所拉車的數量成正比，同時與專用線和門吊大車走行線平直度有關），則促使主動車輪發生橫向位移的力：

從（1）式得出，F1 與F和鋼絲繩夾角θ 成正比例關系。當F1 的值達到一定時,可造成大車輪啃道，由于走行梁長期受外力F1 的橫向作用，天長日久，容易使其發生永久變形。實際上，大車輪軸嚴重啃道和走行梁變形，已使輪軸受到不正常的外力，加大了輪軸的彎曲應力，使軸疲勞而發生裂紋。這是拉車造成斷軸的主要因素。

從圖3 可看出，龍巖20／10tC型門吊因拉車造成輪軸徑向截面中心線與走行基礎中心偏離20mm，這是長期拉車造成的后果。

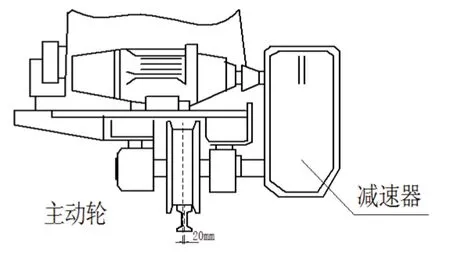
圖3

2.1.2 應力和扭矩計算

根據設計資料，20／10t C型門吊大車運行機構有關參數為：最大運行速度U＝40 ～ 42 m／min；電動機功率N＝11 kW；額定轉速n＝715r／min；傳動比i＝37.7；傳動效率η＝0.95。

斷軸承受的扭矩與應力分別為：

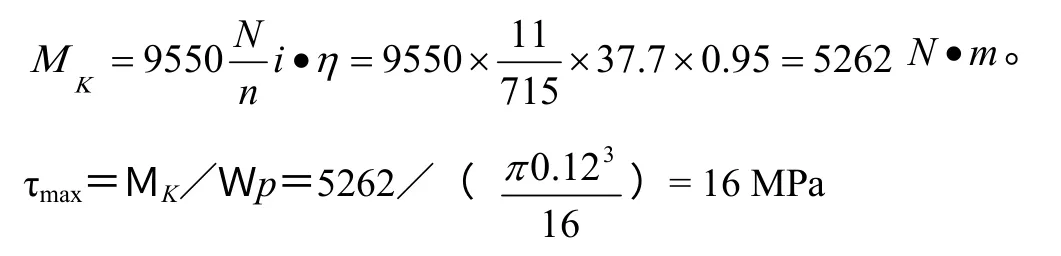
其中，Wp 為抗扭截面系數。

門吊在作業時大車往返運行，軸承受著循環扭矩作用。鑒于大車空載和負載運程的運動阻力相差不大，可偏于安全地近似看成對稱循環，幅值τa＝τmax＝16MPa。

按原設計要求，大車主動輪軸材料為40Cr ,并經調質（淬火后高溫回火）處理，要求HB241～262。

根據鋼材硬度與強度近似線性關系式，當硬度在HB 150～400 之間時

從機械設計手冊查得，軸的許用安全系數〔n〕＝1.6，按圖紙要求40Cr 調質處理，σb＝787 MPa，σ1＝359 MPa，換算得τ1＝201 MPa，根據σb可查得有效應力集中系數為Kτ＝1.76，尺寸系數0.75，粗車表面加工系數為β＝0.9，則工作安全系數為：

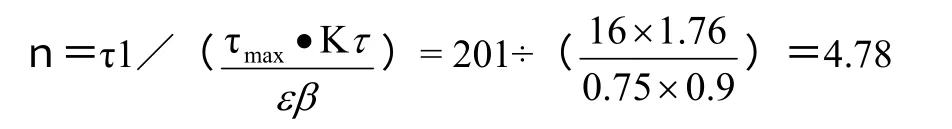
由于n＞ 〔n〕，因此可以斷定40Cr 的軸是能滿足疲勞強度要求的。

但這一計算過程中，沒有考慮沖擊載荷的影響，在司機采用反接制動或點動定位時，瞬間尖鋒載荷很大，這當然也是導致早期失效的原因。

2.1.3 力的計算

2.1.3.1 車輪傳遞的轉矩（受力如圖6(a)、(b)所示） 2.1.3.2 計算最大垂直輪壓（徑向力）Q

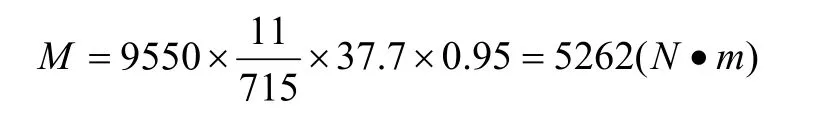
在門吊拉車過程中，一般是空載（即起升機構處于非工作狀態）拉車，而且是小車處于有效懸臂處的情況下拉車為多數。為了計算方便，本文不考慮梯子、電纜懸筒、大小車緊急制動等對輪壓的影響，并把小車重心與起升中心線合二為一作為研究狀態。 圖4 所示為門吊空載拉車（小車處于懸臂處）輪壓計算簡圖。

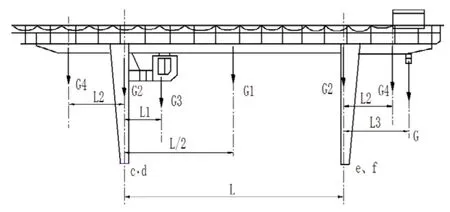
圖4

G——小車自重（10.98t）。

G1——上部主梁跨中部分重量（15.7t）。

G2——支腿重量（14.35t）。

G3——司機室重量（0.98t）。

G4——上部主梁懸臂部分重量（6.5t）。

L—— 跨度（22.5m）。

L1——司機室重心至大車軌道中心線距離（2.5m）。

L2——懸臂重心至大車軌道中心線距離（4.5m）。

L3——小車及機械設備重心至大車軌道中心線距離（7m）。

由圖5 可知：

Re＝（Rmax·5000）／9000＝24（t）

Re 即為主動輪輪壓。Re＝Q＝24（t）

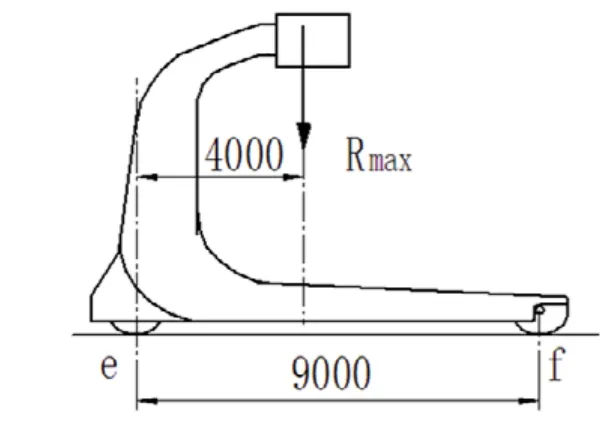
圖5

2.1.3.3 最大摩擦阻力P

最大摩擦阻力P由車輪沿軌道滾動摩擦阻力P1和起重機運行發生歪斜時（大車走行軌道變形）車輪輪緣與軌道側面摩擦所引起的附加摩擦阻力P2合成。

式中，K——滾動摩擦系數，K＝0.08；μ——車輪軸承摩擦系數，μ＝0.015；K附——附加阻力系數，K附＝1.5；d——滾動軸承內徑（厘米）；D輪——車輪直徑（厘米）。

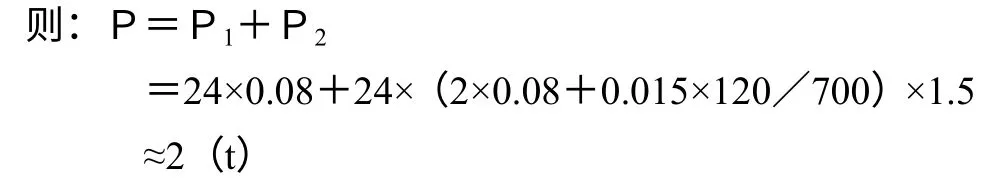
2.1.3.4 軸向力N

主動車輪因受F1（圖2 所示）作用，將向垂直于大車走行軌道方向滑動，其滑動摩擦力P滑＝Q·K1＝24×0.12＝2.88（t）（如圖7所示），其中K1為滑動摩擦系數。

當F1＞P滑時,車輪發生橫向位移（滑動），以致車輪輪緣與軌道摩擦，形成啃道。因此軸向力N≥P滑。

2.1.3.5 外力分析

由車輪軸受力分析，得出軸的計算簡圖，如圖6(c)所示。

圖6

m＝P·D／2＝2×1000×10×0.7／2＝7000N·m

mc＝N·D／2＝2.88×1000×10×0.7／2＝10080N·m

力Q和力偶距mc 使軸在垂直面XAY 內產生扭曲變形，力P使軸在水平面XAZ 內產生彎曲變形，力偶矩m使軸產生扭轉變形，軸N使軸產生壓縮變形，因此，車輪軸AB為彎扭壓組合變形。通常，軸力N對軸的壓縮作用與彎曲、扭轉相比很小，可忽略不計，則將軸簡化為彎扭組合變形。

2.1.3.6 內力分析并畫彎矩圖和扭矩圖

軸在垂直面XAY 受力情況為圖6(d)所示，由平衡方程，解得A、B兩支座的反力為：

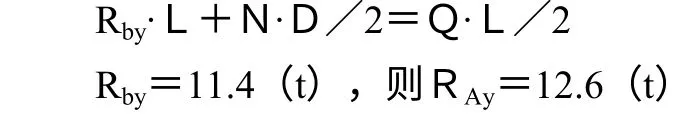
彎矩圖如圖6(e)所示，最大彎矩截面在C處，其值為：

Mcz＝RAy·L/2＝12.6×1000×10×0.325/2＝20475N·m

軸在水平面XAZ 內的受力情況如圖6f 所示，A、B兩支座的反力為：

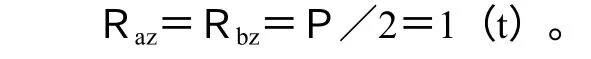
彎矩圖如圖6(g)所示，最大彎矩在C截面處，其值為:

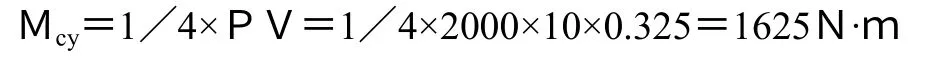
軸在力偶矩m作用下（圖6(h)），扭矩圖如圖6(i)所示，在BC 段內，各橫截面上的扭矩相同，其值為：

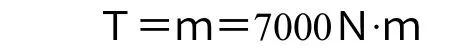
由內力圖可知，橫截面C是危險截面，在此截面上的合成彎矩為：Mc2＝Mcz2＋Mcy2

2.2 強度校核

軸材料為40Cr，其〔σ〕＝100 MPa

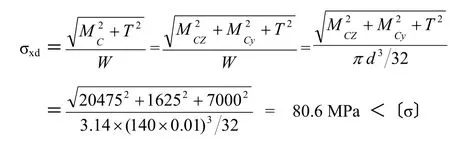
由圖計算結果表明，軸的強度能滿足。

由圖7 可知，當F1＝P滑時，車輪處于平衡的臨界狀態，只需F1稍微比P滑大一些，車輪即發生橫向位移，形成啃道。

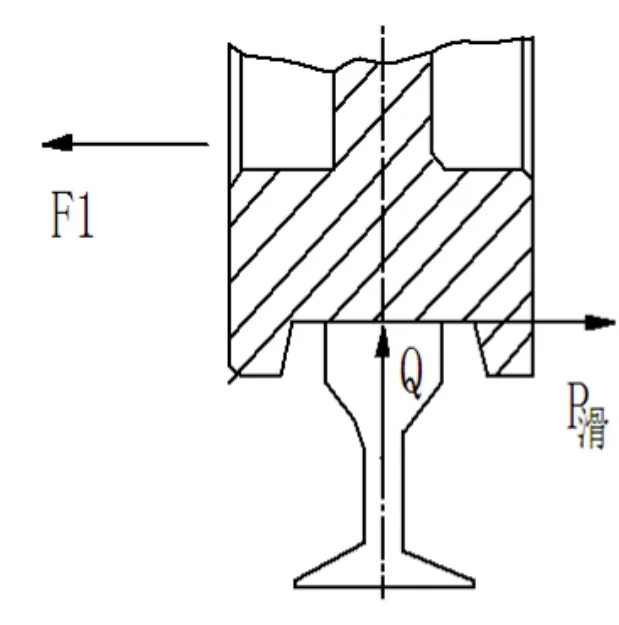
圖7

則此時所拉貨車的數量（或重量），按拉車鋼絲繩9 米計算,由圖2 得出：

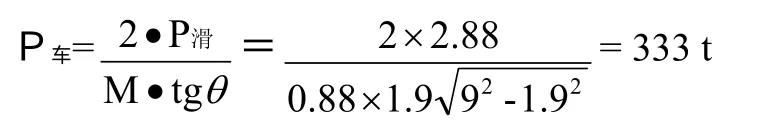
以上計算以貨車軌道、大車走行軌道和鋼絲繩均處水平狀態，不考慮軌道的坡度和鋼絲繩與水平線的夾角等影響。

若按C64 型貨車滿載計算，每個車質量＝自重＋載重＝22t＋61t＝83t，則貨車數量＝333／83≈4（個）

即按上述情況拉車，重車數量達到4 個時，大車輪形成輕度啃道，但軸的強度仍能滿足要求。

現在根據強度計算公式，求出拉車數量達到多少時影響軸的強度。

當σxd＝〔σ〕＝100MPa 時，影響軸的強度。

因為拉車數量的改變，不會使Mcy和T隨之改變，而πd／32 為常數。

由此可知：當Mcz＝25948N·m時， Mcz＝RAy·L／2

故 RAy＝2·Mcz／L×10＝16 t

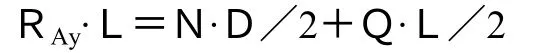
由圖6(d)列平衡方程:-

解得N＝3.72 t

求得拉車數量＝430／83＝5.2（輛）

由此可見，當門吊按前面情形拉重車達到5輛時，不僅會產生嚴重的啃道，同時也會影響軸的強度，就會嚴重縮短軸的壽命，造成斷軸。

本文對其它情形拉車造成大車啃道及斷軸的影響，不另作剖析。

3 結論與建議

3.1 結論

3.1.1 軸的材料系40Cr，經調質處理，按靜態計算其強度滿足要求。

3.1.2 利用龍門起重機大車拉車，造成啃道，使軸的受力發生變化，經兩種情形計算，分別造成啃道和嚴重啃道、危及軸的強度現象發生。

3.1.3 若小車處于另一端懸臂處時大車拉車，由于Q減小，P也減小，故按前兩種情形拉車，更易發生啃道和斷軸現象。

3.2 建議

3.2.1 車輪軸頸過渡圓角半徑不宜偏小，且加工刀痕不能太粗，以減少應力集中。

3.2.2 加大對違章拉車班組或個人的考核力度，以有效杜絕拉車現象發生。

3.2.3 加強現場作業人員愛護設備的思想教育，裝卸部門要協調好與車站的關系，要求運轉不亂甩車，做到送車到位。

[1] GB/T 3811-1983, 起重機設計規范[S].

[2] 張質文等.起重機設計手冊[M].北京: 中國鐵道出版社，2001.

[3] 劉鴻文.材料力學[M]. 北京: 高等教育出版社，2004.