路段擁擠條件下的高速公路匝道協調控制方法

柴 干 高祥云

(東南大學智能運輸系統研究中心,南京 210096)

隨著高速公路車輛保有量的增長,路段擁擠狀況不斷出現.當路段出現擁擠時,會形成道路瓶頸,產生嚴重的車輛延誤現象[1].若未對擁擠路段進行及時控制,上游車輛對其不斷沖擊將導致交通環境惡化,降低路網交通的整體效益.緩解交通擁擠,提高運營效率與安全性,已經成為亟待解決的現實問題[2].研究表明,匝道協調控制是緩解高速公路擁擠的最有效控制方式[3].開展擁擠條件下的匝道協調控制方法研究,對緩解擁擠、提高通行能力具有理論與工程應用價值.匝道協調控制主要包括最優控制、多變量控制、模糊控制和啟發式控制.最優控制通過優化性能指標,使主線交通處于期望狀態[4],但算法復雜、計算量大,難以建立擁擠下的控制方案.多變量控制使交通狀態維持在設定值附近,含有反饋機制,可減少誤差并抵抗干擾,但擁擠時控制效果并不理想[5].模糊控制不需要抽象模型,利用專家經驗克服原始數據的誤差[6],但對于多個匝道的協調控制,模糊規則呈指數增加,難以應用于實際中.啟發式控制無需確定控制目標,基于經驗和實測數據,采取局部與協調結合的方法生成調節率,技術復雜性低、可實施性好[7].

啟發式協調控制方法已經成功應用于美國高速公路的匝道控制中[5].其中,Zone算法具有實時性與靈活性,但由于控制目標不清楚且沒有充分考慮交通突變,難以應對交通擁擠;Helper算法無需準確的OD信息和交通流模型,但由于缺乏優化目標,難以實現優化控制,并且不具備預測機制,難以避免時滯引起的控制誤差.Swarm算法依據預測交通參數識別交通瓶頸,期望在萌芽階段消除交通擁擠;但是該方法需要準確的預測模型和精確的OD數據,才能實現調節率的合理選擇.Bottleneck控制方法具有實時性、靈活性和邏輯簡單等特點,可通過改進控制策略的魯棒性和時滯性,提高解決路段交通擁擠的有效性.

為了充分利用Bottleneck控制方法的優點,克服其缺陷,以解決擁擠條件下的匝道控制問題,本文依據擁擠持續時間內交通流波陣面向上游移動的距離,推導擁擠影響范圍,獲得需要調節的匝道數.然后,通過變換控制變量,對局部調節率和協調調節率進行優化,獲得改進的Bottleneck控制方法,克服原方法超調量過大、調節時間過長的缺陷.

1 Bottleneck控制方法

1.1 局部調節率

通過測得匝道上、下游鄰近處的占有率,根據調節率-占有率曲線,采用在線查表法[8]確定該匝道的局部調節率,即

(1)

式中,R(j,k)為周期k內匝道j的局部調節率;Pu,Pv分別為占有率-調節率曲線上控制點u,v的相應占有率;Ru,Rv為Pu,Pv對應的調節率;P(j,k)為周期k內匝道j上游的主線占有率.

1.2 協調調節率

若路段i下游占有率超過閾值,出現交通瓶頸,則

P(i,k-1)≥Pc(i)

(2)

Qup(i,k-1)+Qon(i,k-1)≥Qoff(i,k-1)+

Qdown(i,k-1)

(3)

式中,P(i,k-1)為周期k-1內路段i的下游占有率;Pc(i)為路段i的下游占有率閾值;Qup(i,k-1),Qdown(i,k-1)分別為周期k-1內路段i的上、下游流進交通量;Qon(i,k-1),Qoff(i,k-1)分別為周期k-1內路段i內的入、出口匝道流出交通量.

針對每一個瓶頸路段i,計算其上游各入口匝道調節率的降低總量,并按照經驗權重將降低總量分配至相關入口匝道.權重系數根據上游入口匝道到路段i的距離設定,即

Qreduction(i,k)=[Qup(i,k-1)+Qon(i,k-1)]-

[Qoff(i,k-1)+Qdown(i,k-1)]

(4)

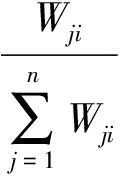
(5)

式中,Qreduction(i,k)為周期k內路段i上游關聯入口匝道流入的降低流量;Rreduction(j,i,k)為周期k內路段i上游關聯入口匝道j流入的降低流量;n為需要協調的匝道數;Wji為路段i上游關聯入口匝道j的權重系數.各瓶頸路段的影響區域可能發生重疊,每個入口匝道常會處于不同瓶頸路段的影響區域中.因此,需要選取各瓶頸路段的入口匝道流入交通降低值中的最大值,作為各個匝道的協調調節率,即

(6)

式中,Qon(j,k-1)為周期k-1內匝道j的實際流入量;r(j,k)為周期k內匝道j的協調調節率.

1.3 最終調節率

將局部層面和協調層面上匝道j的調節率R(j,x)和r(j,k)進行比較,取最小值作為匝道j的最終調節率Rend,即

Rend=min[R(j,k),r(j,k)]

(7)

Bottleneck控制方法的不足在于:① 協調層面上,缺乏需要調節的入口匝道數量和位置的準確表達式.② 主線最大流量隨時間、天氣等因素的變化而變化,故將流量作為控制變量,難以確切反映主線的交通瓶頸;臨界密度則相對穩定且不受天氣等因素的影響,故將密度作為控制變量,適于反映主線的交通擁擠狀態.③ 頻繁對局部調節率和協調調節率取極小值,易形成主線交通運量的欠載或過載現象.

2 改進的Bottleneck控制方法

2.1 控制匝道數的識別

根據路段擁擠時交通波運行機理,應用Greenshields模型推導擁擠影響范圍,并結合匝道樁號確定所需調節的匝道數與位置.設ρi為路段i的堵塞密度,路段i有2個相鄰且不同密度的區域ρi1和ρi2,用垂直面S加以分割(稱S為波陣面);交通波的波速為ω,且按圖中箭頭x方向運行(見圖1).

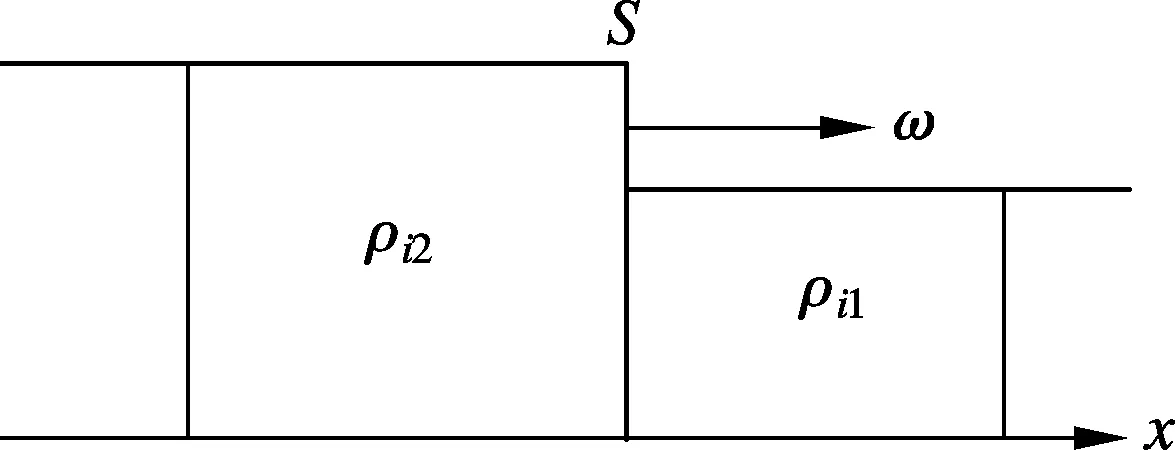
圖1 交通波示意圖

高速公路發生擁擠致使車輛難以通行時,上游車輛將在波陣面S處開始排隊.根據交通波波速和Greenshields模型的車流速度-密度線性關系,求得擁擠點上游影響范圍L為

(8)

式中,μf為自由流車速；T為擁擠持續時間.

擁擠狀態下的匝道控制即是對擁擠點上游流入交通進行控制.從探測到擁擠時刻開始,就需要估計匝道控制范圍,確定需要進行協調的匝道數n,其計算公式為

n={L,Xn}

(9)

式中,Xn為波陣面上游第n個匝道的樁號.傳統的匝道協調方法沒有給出需調節的匝道數量與位置,故實際操作性不強.此處定義XS為波陣面樁號,在[XS,XS+L]內,得到用于辨識匝道數n及其位置的表達式為

(10)

n的確定還與高速公路具體的結構有關.當L相同、匝道間距不同時,n的取值一般不同.

2.2 匝道流入交通降低量的確定

控制變量是反映交通控制系統特性的關鍵參數,其選取的合理性直接關系到控制效果.本節將依據流量與密度的關系,闡述應用密度代替流量作為控制變量的原理,并采用比例積分控制方法,推導流入交通降低量的表達式.交通流量和密度的關系如圖2所示.圖中,ρm為最大流量qm對應的密度.任一流量值q對應2個密度值ρi1和ρi2,前者小于ρm(即位于不擁擠區域),后者大于ρm(即位于擁擠區域).交通擁擠時,事發點上游密度變大,下游密度變小,而上、下游交通量的計算值可能相差并不大[9],故Qreduction可能很小.若按照經驗權重將Qreduction分配至各個關聯匝道,則難以實現擁擠條件下的控制效果,故需要對Qreduction的計算公式進行改進.

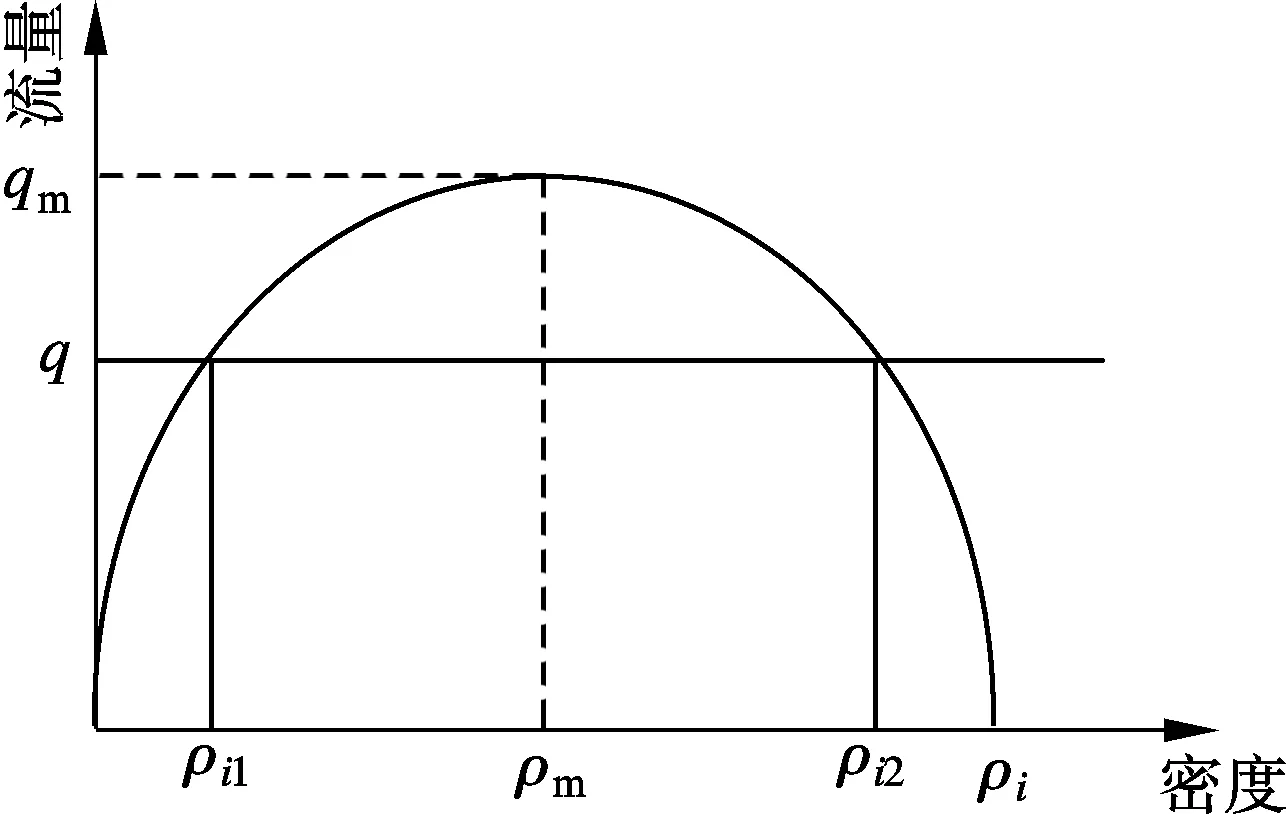
圖2 交通流量和密度的關系圖

PID控制器采用反饋控制方式控制變量與期望值的誤差,其積分單元用于消除穩態誤差,比例和微分單元用于加快控制反饋.由于微分項產生沖擊效應,PID控制器常用于反饋速度較慢的系統[10].將密度作為控制變量,則

Qreduction(i,k)=-[K1e(i,k)+K2(e(i,k)-e(i,k-1))]

(11)

式中,K1,K2為PID的控制參數[11],由實驗獲得;e(i,k)為周期k內的控制誤差.將e(i,k)=ρd-ρS(i,k)代入式(11)可得

Qreduction(i,k)=-(K1+K2)[ρd-ρS(i,k)]+

K2[ρd-ρS(i,k-1)]=-K1ρd+

(K1+K2)ρS(i,k)-K2ρS(i,k-1)

(12)

式中,ρd為擁擠點上游的期望密度;ρS(i,k)為周期k內路段i中波陣面S的上游密度.

將式(12)代入式(5),則

Rreduction(j,i,k)=[-K1ρd+(K1+K2)ρS(i,k)-

(13)

2.3 最終調節率的優化

路段擁擠時,Bottleneck控制方法取局部調節率與協調調節率中的較小值,這樣雖然可以迅速減小路段密度,但當路段沒有發生擁擠或交通密度小于期望密度時,容易使超調量過大,并產生較長的調節時間.對其進行改進的思路為:當被調密度大于期望密度時,按照最嚴格的方式調節(取局部調節率與協調調節率中的較小值);當實際密度小于期望密度時,對調節率進行重新取值,最終調節率取局部調節率和協調調節率的加權組合,即

(14)

式中,ρtarget=35 pcu/(km·lane)為路段i的密度理想值[11];αj為匝道j的比例因子，且0≤αj≤1.

3 仿真示例與分析

選取寧杭高速溧陽西至丁山6個路段作為示例路徑,路徑拓撲圖見圖3.

圖3 寧杭高速公路路徑的拓撲圖

3.1 參數初始化

交通擁擠發生時,檢測器檢測到的各路段密度和調節率初值見表1.由表可知,第6路段(即丁山路段)的密度大于期望密度,發生擁擠.

表1 各個路段的初始密度與初始調節率

根據該路段交通運行的基本狀況,設期望密度為35 pcu/(km·lane);上游主線進入的流量平均值為6 000 pch/h;仿真步長為20 s;仿真時間為2 000 s.仿真實驗中,K1=97,K2=29時,期望密度的動態跟蹤性能較好.對寧杭高速上296起碰撞或拋錨等事件持續時間進行統計分析,取事件持續時間T=60 min,代入式(8)得事件影響范圍為19.6 km.根據式(10)得事件影響范圍內的匝道為丁山、宜興和西塢.協調層面的調節率分配權值可根據匝道與擁擠斷面的距離決定,離擁擠斷面越遠,匝道承擔的調節率降低值越小.

3.2 比例因子的敏感性分析

根據改進的Bottleneck控制方法,應用數字仿真技術,分別對丁山、宜興、西塢3個入口匝道的比例因子αj(j=1,2,3)進行敏感性分析.當αj=0,0.2,0.4,0.6,0.8,1.0時,相應路段密度隨時間變化的曲線見圖4.

當權重系數為1.0時,密度曲線快速且平穩地變化,超調量小,調節時間少,幾乎無振蕩,控制效果最為理想,可以使路段交通密度快速平穩地達到所期望的目標值.

由此可知,針對本示例,式(14)實際演變為

(15)

3.3 控制算法的比較

采用Bottleneck控制方法、改進的Bottleneck控制方法以及未施加控制方法時,對擁擠路段及其上游相鄰路段進行仿真分析，路段車流密度隨時間的變化軌跡見圖5.由圖可知,未施加控制方案時,3個路段的擁擠狀況隨時間延長而加劇,并逐步影響上游各路段.在路段發生擁擠時,利用Bottleneck控制方法,取局部調節率與協調調節率中的較小值可以迅速減小路段密度.當路段沒有發生擁擠時,仍然采用局部調節率與協調調節率中的較小值,將產生較大的超調量和較長的調節時間.控制變量需要經過1 500 s才能穩定在理想密度上,且期望密度與路段密度的最大絕對誤差達到11 pcu/(km·lane).利用改進的Bottleneck控制方法,能夠迅速使擁擠的第6路段(丁山段)在450 s時消散擁擠,達到平穩交通流狀態.由于采取了優化的匝道調節率,有效避免了原Bottleneck控制方法的不足,使調節時間減少70%,超調量減小75%,無余差且幾乎無振蕩.利用該方法不僅能迅速疏導路段擁擠,而且能夠使擁擠路段的上游路段密度快速趨向期望密度,保持路徑上交通流運行的通暢與穩定.

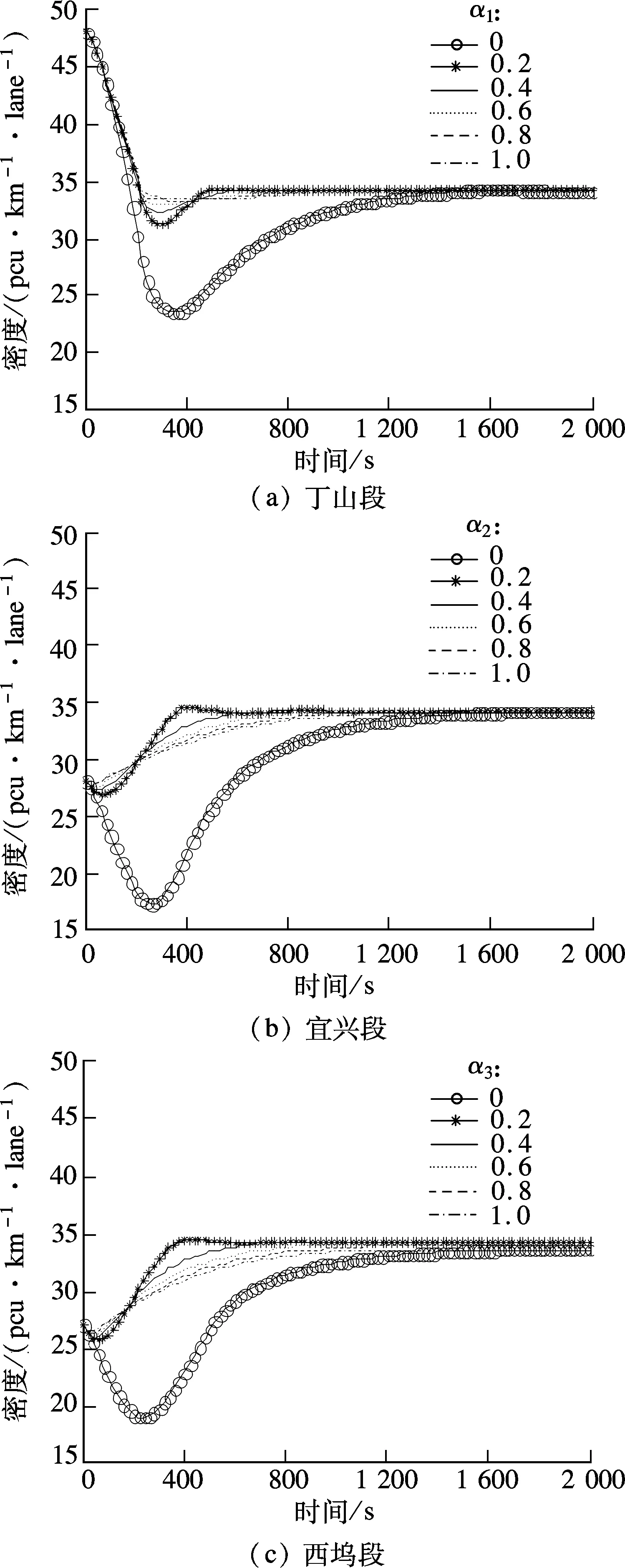
圖4 比例因子的敏感性分析

圖5 控制方法的比較結果

4 結語

基于交通波理論推導的交通擁擠影響范圍,能夠辨識影響范圍內需要協調控制的匝道數量及位置,為改進Bottleneck控制方法提供關聯入口匝道權重系數的計算依據.針對Bottleneck控制方法使用流量累積判別動態交通狀況,難以檢測主線交通擁擠狀態的缺陷,以密度代替流量作為控制變量,設計PID控制器,構建改進的Bottleneck控制方法,從而將流量囤積調節轉變為密度擁擠控制.調節路段流量累積，使控制變量接近期望值時會產生調節過度現象,通過對局部調節率和協調調節率進行組合,確定優化的最終調節率,則可解決調節過度的問題.

)

[1]Papamichail I,Papageorgiou M.Heuristic ramp-metering coordination strategy implemented at monash freeway[J].TransportationResearchRecord,2010,2179: 10-20.

[2]張海軍,張鈺,楊曉光.異常事件下高速道路交通狀態的分析與仿真[J].交通運輸工程學報,2008,8(2):116-121.

Zhang Haijun,Zhang Jue,Yang Xiaoguang.Analysis and simulation of traffic state on expressway during incident[J].JournalofTrafficandTransportationEngineering,2008,8(2): 116-121.(in Chinese)

[3]Chai Gan,Xie Yongli.A genetic-fuzzy control application to ramp-mainstream joint coordination control of the freeway[J].AdvancedScienceLetters,2012,7: 369-374.

[4]Kotsialos A,Papageorgiou M,Mangeas A.Coordinated and integrated control of motorway networks via nonlinear optimal control[J].TransportationResearchPartC:EmergingTechnologies,2002,10(1): 65-84.

[5]Papageorgiou M,Kotsialos A.Freeway ramp metering: an overview[J].IEEETransactionsonIntelligentTransportationSystems,2002,3(4): 171-181.

[6]溫凱歌,曲仕茹,張玉梅.基于模糊邏輯的高速公路入口匝道控制方法[J].中國公路學報,2007,20(6): 100-104.

Wen Kaige,Qu Shiru,Zhang Yumei.Method for freeway on-ramp control based on fuzzy logic[J].ChinaJournalofHighwayandTransport,2007,20(6): 100-104.(in Chinese)

[7]Papamichail I,Papageorgiou M.Traffic-responsive linked ramp-metering control[J].IEEETransactionsonIntelligentTransportationSystems,2008,9(1): 111-121.

[8]Jacobsen L,Henry K.Real-time metering algorithm for centralized control[J].TransportationResearchRecord,1989,1232: 17-26.

[9]Zhang H M.Coordinated Traffic responsive ramp control via nonlinear state feedback[J].TransportationResearchPartC:EmergingTechnologies,2001,9(5): 337-352.

[10]Sheu J B.Stochastic modeling and real-time prediction of vehicular lane-changing behavior[J].TransportationResearchPartB:Methodological,2001,35(7): 695-716.

[11]梁新榮,劉志勇,徐建閩.高速公路多匝道協調控制系統設計與仿真[J].信息與控制,2005,34(3):308-311.

Liang Xinrong,Liu Zhiyong,Xu Jianmin.Design and simulation of coordinated ramp control system on freeway[J].InformationandControl,2005,34(3): 308-311.(in Chinese)