環氧瀝青混合料細觀尺度水損壞特性

胡 靖 錢振東

(東南大學智能運輸系統研究中心, 南京210096)

環氧瀝青混合料(EA)是大跨徑鋼橋面的主要鋪裝材料之一,是由集料和瀝青砂漿所組成的多相混合料.水對EA的影響十分復雜,一方面,水分降低了瀝青混合料的強度,使其在載荷作用下容易出現破壞;另一方面,集料的化學和熱力學性質決定了集料對水的吸附性大于對瀝青砂漿的吸附性,因此水分會逐漸浸入集料與瀝青砂漿的黏結面,直至兩者剝離.在細觀結構上可以理解為瀝青砂漿在水分作用下模量和黏結力的衰減.

針對水分對瀝青混合料的影響,文獻[1-2]主要從宏觀角度進行研究,但無法在本質上揭示混合料內部各組分的影響機理.采用有限元數值技術進行瀝青混合料的細觀力學研究已成為分析內部組分影響的有效途徑.Bandyopadhyaya等[3]通過有限元軟件建立瀝青混合料的細觀力學模型,預測了集料為不規則形狀與橢圓形顆粒時的力學行為,較好地模擬了混合料裂縫的大小及位置;Dai[4]利用細觀模型分析了瀝青混合料的動態模量和相位角等黏彈性質,表明細觀模型是預測瀝青混合料黏彈性能的有效方法;Arambula等[5]則利用瀝青混合料細觀模型分析了水汽擴散運動的機理及影響因素,指出混合料中水分擴散系數對水損破壞有直接關系.近年來,Liu等[6]通過內聚力模型(CZM),在瀝青混合料劈裂模型中預設裂縫,模擬了裂縫萌生與擴展變化過程中試件的力學狀況;Caro等[7]采用CZM模擬瀝青混合料中集料與瀝青砂漿的黏結界面,研究了瀝青混合料中水汽對混合料力學強度、材料性質及加載情況的影響,表明采用有限元方法研究水損破壞的可行性[7].盡管已有學者進行了瀝青混合料細觀力學水損方面的研究,但很少涉及不同水分擴散狀態下的混合料力學變化情況.因此本文使用ABAQUS有限元軟件建立EA細觀力學與流體滲透模型,分析干燥、部分飽和以及完全飽和情況下瀝青混合料內部的應力應變以及集料與瀝青砂漿黏結界面裂縫的萌生、擴展直至失效的過程.

1 瀝青混合料內聚力模型

CZM是模擬黏結面逐步分離的力學計算方法,最初用于模擬脆性材料的斷裂過程.CZM的本構關系由內聚力區域單元的牽引-分離定律(traction-separation law)所定義,該定律描繪了界面上的黏聚力與單元厚度方向上2個面之間相對位移的關系[8].ABAQUS中提供了線性與指數2類本構關系的內聚力單元(cohesive element),文獻[9]指出線性本構模型較適合模擬瀝青混合料斷裂特性,如圖1所示.圖中,T為裂縫前段微小區域內的內聚力,即黏聚力;Tc為黏聚力極值;δ為分離界面的相對位移;δn與δf分別對應軟化點及最終破壞的相對位移.

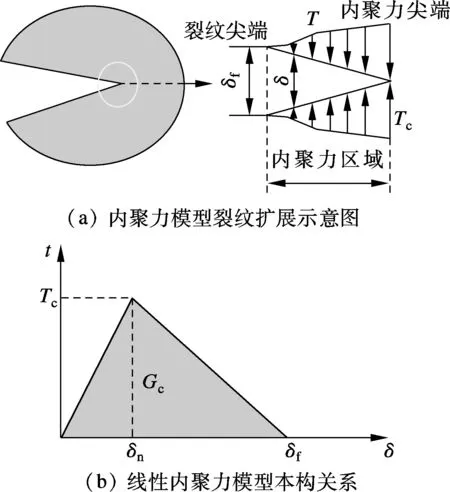
圖1 內聚力模型原理與線性本構關系圖

線性內聚力本構由2部分組成:在初始損傷發生前(內聚力小于Tc,且相對位移小于δn)的線性關系和單元達到初始損傷后的線性軟化過程.在理論上,初始損傷處的內聚力達到Tc后材料出現開裂破壞,而線性本構關系曲線下方的面積即為材料的斷裂能.采用界面黏結單元模擬裂紋的萌生與擴展,其初始損傷準則為最大名義應力判據:

(1)

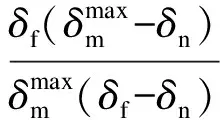
(2)

模型中分別采用三角形平面應變單元(CPE3)和帶孔隙水壓性質的四邊形平面應變單元(CPE4P)對瀝青砂漿與集料劃分網格,在每個集料的四周建立厚度為0.1 mm的界面黏結平面單元,用于模擬集料與周圍瀝青砂漿的黏結作用.在局部區域采用較細網格,以確保計算精度,細觀模型及其有限元網格劃分如圖2所示.

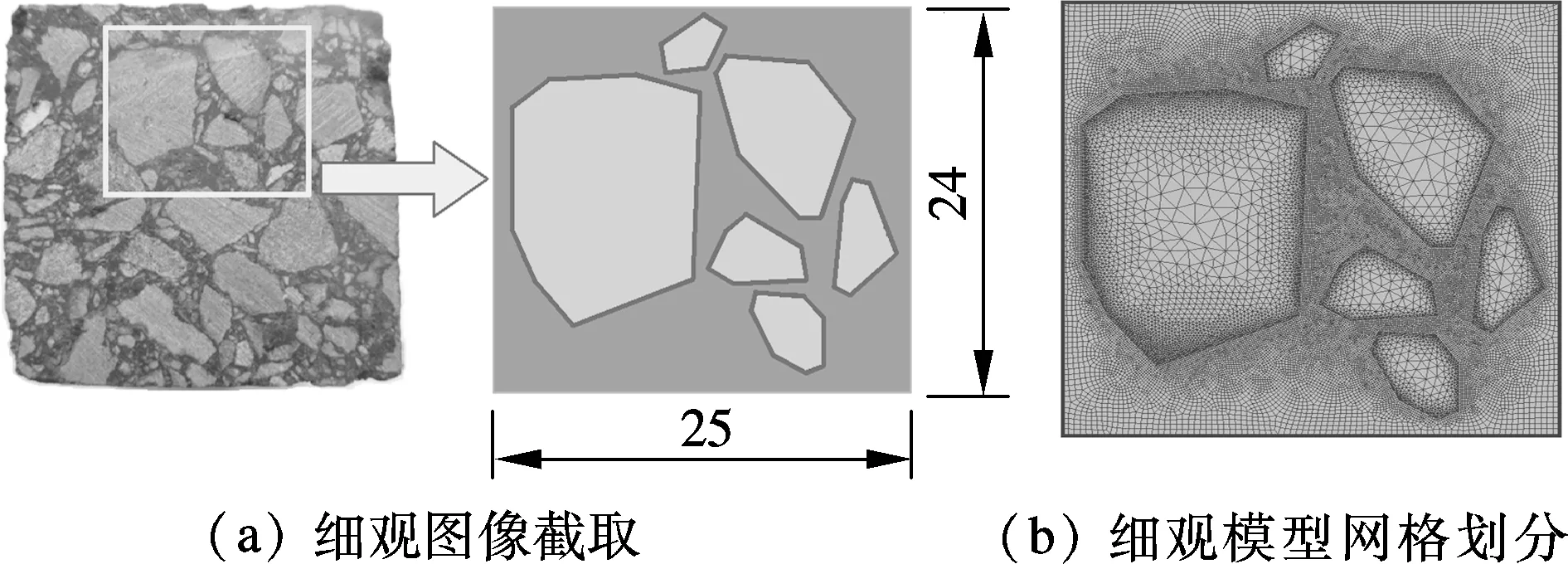
圖2 EA細觀有限元模型建立圖示(單位：mm)

為了保證瀝青砂漿與界面黏結單元變形的協調性,假設兩者的材料參數取值相同，隨著含水率的不同產生線性變化,部分材料參數取自文獻[10],列于表1.

表1 細觀模型材料參數

2 荷載-水分擴散有限元細觀模型

瀝青混合料細觀力學模型分析采用流體滲透/應力耦合分析類型.在滲流過程中,對模型施加逐漸增大的均布載荷,增幅恒定為0.05 MPa/s.由于實際車輛載荷對鋪裝層的作用時間遠小于結構的滲流時間,因此假設瀝青混合料的孔隙率不隨模型的變形改變且滲流狀態與所處的應力狀態無關.

細觀模型的水分滲透遵循Forchheimer定律,假定模型上表面受滲透水壓,下表面設為排水邊界,兩側則為不排水邊界.由于滲透水壓的作用,模型內部各點的含水率隨時間不斷發生變化,即出現水分擴散現象,如圖3所示.

圖3 瀝青混合料細觀模型水分擴散過程

假設隨著瀝青混合料中瀝青砂漿與界面黏結層含水率的變化(由干燥到完全飽和),各項參數均由干燥時的初始值線性衰減至完全飽和時初始值的一半,因此本文利用場變量技術來研究瀝青混合料水損壞過程中材料參數的變化.

3 荷載-水耦合作用下瀝青混合料水損壞細觀數值仿真

本節對界面黏結單元與混合料內部砂漿單元兩者的受力特性進行分析,研究在荷載-水耦合作用下EA內部的力學響應.

3.1 細觀模型黏結界面斷裂狀態分析

載荷作用下瀝青混合料內部會產生復雜的力學響應,集料與瀝青砂漿黏結界面中過大的應力應變會導致黏結狀態的失效,特別是在有水分參與作用的情況下.本研究中,模型內部各單元處的含水率隨時間的增加而增大,這將直接導致瀝青砂漿與界面層材料性能的衰減.

表2和圖4分別反應了不同含水率情況下集料與瀝青砂漿由于載荷作用,導致黏結界面隨作用時間而出現破壞的發展情況.

表2 不同含水率下黏結界面失效時間 s

不同含水率對黏結界面失效點位置與失效時間都有較大的影響.完全干燥情況下,集料與瀝青砂漿的黏結界面在載荷作用下出現第1個失效點的時間是133 s,相對于部分飽和與完全飽和情況下的92 s和71 s,分別高出30.8%和46.6%,表明瀝青混合料在干燥時出現初始破壞所需的載荷要大得多.此外,不同含水率下集料與砂漿的初始失效點位置相同,但后續失效點出現的順序有所改變.也可看出,隨著含水率的上升,瀝青混合料的破壞程度與速率均朝著不利的方向發展,表現為在載荷相同的情況下,發生剝落的集料顆數隨著含水率的上升而增加.由圖4還可發現,最容易發生剝落的是體積較大且形狀較為不規則的集料.

圖4 不同含水率集料剝落情況

在不同含水率下,集料與瀝青砂漿黏結界面失效長度與加載時間的擬合關系曲線如圖5所示.式(2)中設破壞水平D處于0.95～1范圍內,計算所有集料周圍界面黏結單元失效長度總和作為黏結界面失效總長度.

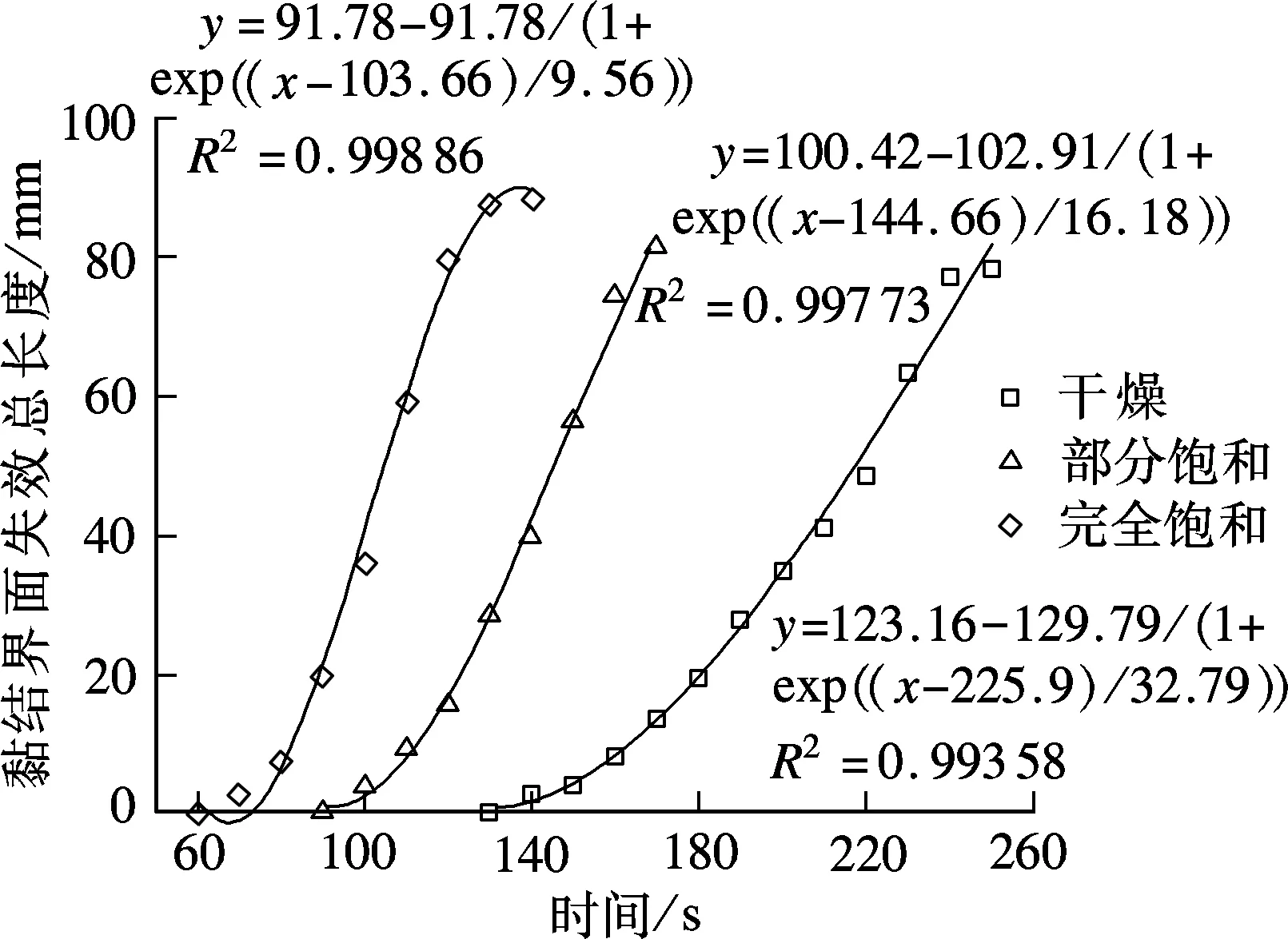
圖5 失效界面總長度隨荷載作用時間的變化

從圖5可看出,失效總長度在發生時間與增長速率方面與含水率有很大的關系.完全飽和時集料與瀝青砂漿黏結界面在加載71 s后萌生裂縫,比部分飽和與干燥狀況下裂縫萌生時間分別早21 s和62 s.曲線也顯示了黏結界面剝離的變化趨勢,即出現初始裂縫后,在載荷的逐漸作用下新裂縫出現的速率逐漸增大,出現一段明顯的快速增長期,最后裂縫增長速率逐漸減小并趨于穩定.材料處于干燥狀態的瀝青混合料,產生相同長度的黏結界面裂縫需要更大的載荷,說明了保證瀝青混合料的干燥狀態或相對較低的含水量對抵抗裂縫、剝落等病害是有利的.

圖6為瀝青混合料最不利受力點處界面黏結單元的最大主應力隨載荷作用時間的變化曲線圖.分析結果表明,在不同含水率情況下,集料與瀝青砂漿的剝落破壞出現時間存在較大的差異.在出現初始破壞前,其最大主應力與加載時間呈現線性變化關系且不同含水率下的應力大小相似,但是界面黏結單元在發生初始破壞、損傷累積直至完全失效的過程中,其最大主應力的變化并沒有遵循線性規則,而是呈拋物線衰減,這主要是由于含水率的變化改變了材料性質以及黏結單元的失效并非由于純拉或純剪,而是復合破壞所致.

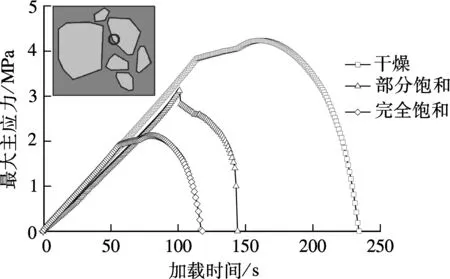
當瀝青混合料處于干燥狀態時,材料性能并不受到水分的影響,界面黏聚力較大,只有在加載時間足夠長(載荷足夠大)的情況下才能發生破壞,其發生初始損傷時的最大主應力超過了4 MPa;隨著材料含水率的增加,部分飽和時和完全飽和時發生初始損傷時的最大主應力分別為3.1 MPa和2.1 MPa,分別比干燥時的最大主應力減少27%和50%.

3.2 瀝青混合料細觀尺度受力狀態分析

瀝青混合料在豎向載荷作用下,由于橫向拉應力的作用,容易出現裂縫病害.為了分析瀝青混合料在荷載-水耦合作用下細觀結構的力學響應情況,選取圖7(a)中所示的細觀混合料模型豎向中線處應力應變作為研究對象,研究載荷作用下橫向應力、應變在豎向中線處的變化趨勢,如圖7所示.

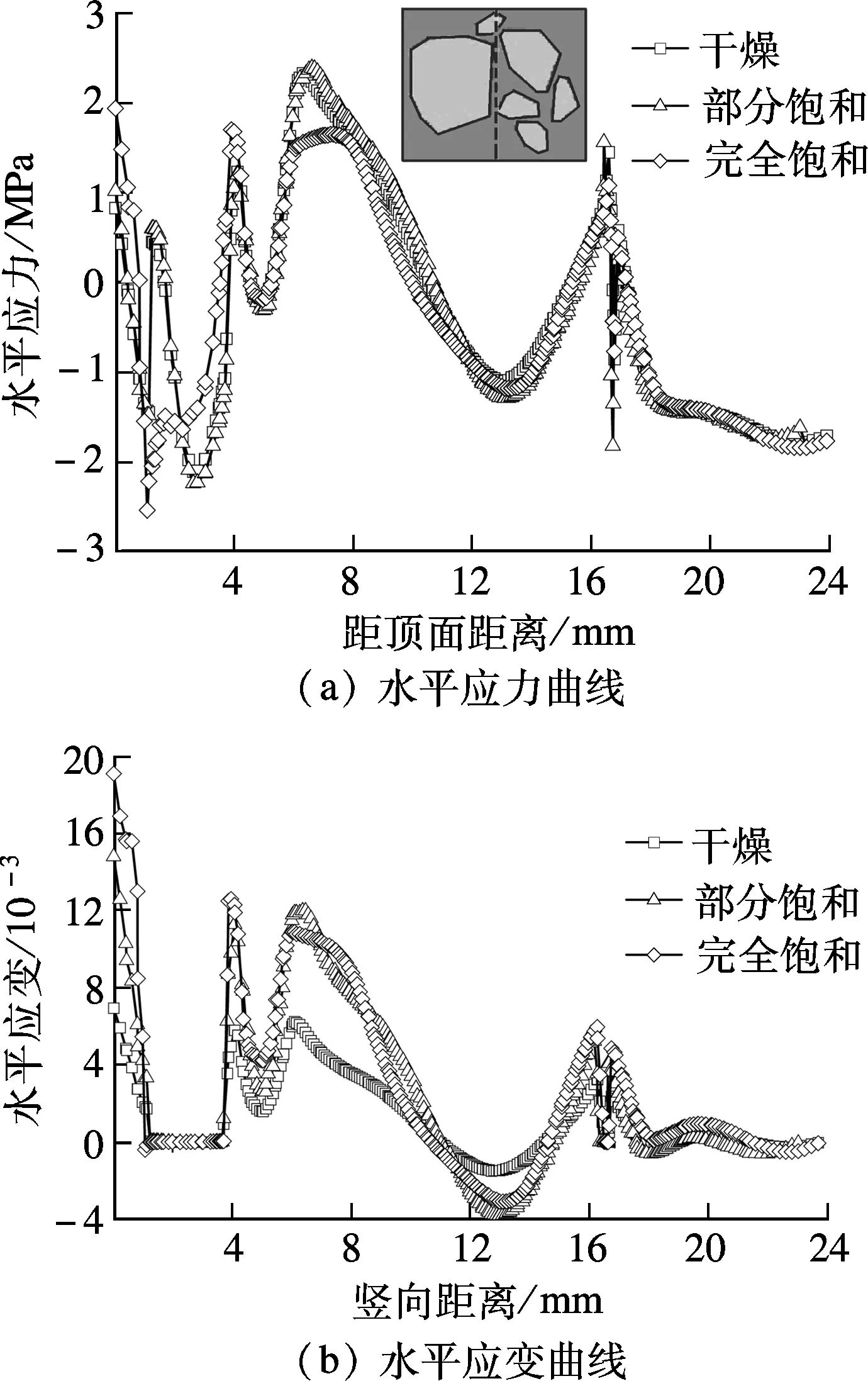
圖7 瀝青混合料豎向中線處應力和應變曲線

由圖7(a)可知，曲線變化趨勢總體上是相似的,并沒有因為水分的影響而出現較大的差異.圖中數據表明,瀝青混合料中的集料主要承受水平壓應力,而瀝青砂漿沿豎向中線的橫向應力分布要復雜得多,在靠近集料的部位表現為拉應力,而遠離集料的部位則表現為壓應力,說明在集料與瀝青砂漿的黏結界面以及在集料附近的瀝青砂漿區域都是處于橫向受拉狀態,容易產生開裂破壞.因此,不同含水率條件下,集料附近的瀝青砂漿受力最不利,且由于集料與砂漿黏結界面的分離,極易產生裂縫破壞.

圖7(b)曲線中除貫穿集料部分的應變接近于0外,其他部分大多呈現拉應變狀態.相對于應力變化,應變曲線受不同材料含水率的影響較大,基本上表現為含水率越高,混合料所受的拉應變越大,這主要是由于材料性能受含水率的增加而出現衰減所致.

4 結論

1) 水分的存在對EA中集料與瀝青砂漿的黏結極為不利,隨著混合料含水率上升,集料與瀝青砂漿剝離的程度趨于嚴重,且水損病害首先發生在體積較大、形狀不規則的集料四周.

2) 在不同含水率下,界面發生剝離的時間與長度不同.處于干燥狀況的瀝青混合料出現相同界面裂縫需要更大的外部載荷以及更長的作用時間.

3) 黏結界面失效點處的最大主應力在不同含水率下的變化趨勢相同,但干燥時最大主應力為4.2 MPa,分別是部分飽和以及飽和狀態下的1.4倍和2倍.

4) 瀝青砂漿在靠近集料的部分主要表現出較大的拉應力,而遠離集料的部分則為壓應力.說明集料與瀝青砂漿的黏結界面及其附近區域都處于不利的受力狀態.

本文尚未考慮不同溫度下瀝青砂漿的黏彈塑性材料參數,將在下一步進行研究.

)

[1]姜旺恒,張肖寧,李智. 基于動水壓力模擬試驗的瀝青混合料水損壞力學機理[J]. 中國公路學報,2011,24(4):21-25.

Jiang Wangheng, Zhang Xiaoning, Li Zhi. Mechanical mechanism of moisture-induced damage of asphalt mixture based on simulation test of dynamic water pressure [J].ChinaJournalofHighwayandTransport, 2011,24(4):21-25. (in Chinese)

[2]郭乃勝,譚憶秋,趙穎華. 動荷載下飽水瀝青路面黏彈性分析[J]. 土木工程學報,2012,45(2):187-190.

Guo Naisheng, Tan Yiqiu, Zhao Yinghua. Viscoelastic analysis of saturated asphalt pavement subjected to dynamic load [J].ChinaCivilEngineeringJournal, 2012,45(2):187-190. (in Chinese)

[3]Bandyopadhyaya Ranja, Das Animesh, Basu Sumit. Numerical simulation of mechanical behavior of asphalt mix [J].ConstructionandBuildingMaterials, 2008,22(6): 1051-1058.

[4]Dai Qingli. Prediction of dynamic modulus and phase angle of stone-based composites using a micromechanical finite-element approach [J].JournalofMaterialsinCivilEngineering, 2010,22(6): 618-627.

[5]Arambula Edith, Caro Silvia, Masad Eyad. Experimental measurement and numerical simulation of water vapor diffusion through asphalt pavement materials [J].JournalofMaterialsinCivilEngineering, 2010,22(6): 588-598.

[6]Liu Jinghui, Wang Duanyi. Numerical simulation of a crack in the cement stabilized stone using cohesive zone models [C]//InternationalConferenceonExperimentalMechanics. Nanjing, China, 2008: 737511.

[7]Caro Silvia, Masad Eyad, Bhasin Amit, et al. Micromechanical modeling of the influence of material properties on moisture-induced damage in asphalt mixtures [J].ConstructionandBuildingMaterials, 2010,24(7):1184-1192.

[8]Shet C, Chandra N. Analysis of energy balance when using cohesive zone models to simulate fracture processes [J].JournalofEngineeringMaterialsandTechnology, 2002,124(4): 440-450.

[9]張東, 黃曉明, 趙永利. 基于內聚力模型的瀝青混合料劈裂試驗模擬[J]. 東南大學學報:自然科學版, 2010, 40(6): 1276-1281.

Zhang Dong, Huang Xiaoming, Zhao Yongli. Simulation of indirect tension test of asphalt mixtures based on cohesive zone model [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2010,40(6):1276-1281. (in Chinese)

[10]Song Seong Hyeok, Paulino Glaucio H, Buttlar William G. A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material[J].EngineeringFractureMechanics, 2006,73(18): 2829-2848.