耦合分?jǐn)?shù)階布朗馬達(dá)在非對(duì)稱勢(shì)中的輸運(yùn)*

王飛 鄧翠 屠浙 馬洪?

1)(四川大學(xué)數(shù)學(xué)學(xué)院,成都 610064)

2)(電子信息控制重點(diǎn)實(shí)驗(yàn)室,成都 610036)

(2012年7月17日收到;2012年9月20日收到修改稿)

1 引言

關(guān)于布朗馬達(dá)[1]問題的研究,最初是源于熱力學(xué)中有關(guān)第二類永動(dòng)機(jī)問題的爭(zhēng)論,以及希望對(duì)一些復(fù)雜的輸運(yùn)機(jī)制給出合理解釋.以往的研究大多集中于對(duì)單個(gè)布朗馬達(dá)輸運(yùn)機(jī)制的分析[2,3],但在許多情況下粒子之間的相互作用是不可避免的,甚至有時(shí)起著決定性作用.最近二十年,在對(duì)耦合布朗馬達(dá)的研究中,發(fā)現(xiàn)耦合能夠促使粒子鏈有更快的平均流速[4,5],而驅(qū)動(dòng)力頻率對(duì)粒子鏈的運(yùn)動(dòng)方向也有顯著影響[6],并且在對(duì)稱周期勢(shì)下粒子鏈也能產(chǎn)生定向輸運(yùn)[7,8]等.隨著分子操縱技術(shù)的發(fā)展,耦合布朗馬達(dá)的定向輸運(yùn)問題開始受到化學(xué)和生物學(xué)等不同學(xué)科領(lǐng)域的密切關(guān)注[9,10].在化學(xué)方面,應(yīng)用Frenkel-Kontorova(FK)模型研究了鏈狀分子十六烷的輸運(yùn)現(xiàn)象[11];在生物學(xué)的分子馬達(dá)研究中,發(fā)現(xiàn)許多稍大的分子馬達(dá)實(shí)際具有復(fù)雜的內(nèi)部結(jié)構(gòu),即具有如雙頭和多頭肌動(dòng)蛋白馬達(dá)這樣的多自由度特殊結(jié)構(gòu),多個(gè)這樣的分子馬達(dá)相互作用時(shí)就會(huì)產(chǎn)生復(fù)雜的輸運(yùn)現(xiàn)象[12,13].但目前關(guān)于耦合布朗馬達(dá)輸運(yùn)現(xiàn)象的研究仍大多局限于整數(shù)階動(dòng)力系統(tǒng)[1?13].

越來(lái)越多的研究表明,粒子在黏性介質(zhì)中的運(yùn)動(dòng)具有“記憶性”,這是整數(shù)階動(dòng)力系統(tǒng)難以刻畫的,而近年迅速發(fā)展起來(lái)的分?jǐn)?shù)階隨機(jī)微分方程理論,則特別適合于描述具有記憶、遺傳和路徑依賴性的物理、化學(xué)和生物學(xué)現(xiàn)象[14,15],為研究耦合布朗馬達(dá)在具有“記憶性”黏性介質(zhì)中的輸運(yùn)現(xiàn)象提供了嶄新的數(shù)學(xué)工具.

本文應(yīng)用分?jǐn)?shù)階FK模型研究粒子鏈在黏性介質(zhì)中的定向輸運(yùn)現(xiàn)象.通過數(shù)值模擬,觀察到整數(shù)階動(dòng)力系統(tǒng)情況下所沒有的定向輸運(yùn)反向流;此外,還討論了階數(shù)、耦合強(qiáng)度和噪聲強(qiáng)度分別對(duì)粒子鏈的平均流速的影響,發(fā)現(xiàn)當(dāng)固定噪聲強(qiáng)度時(shí),粒子鏈的平均流速隨耦合強(qiáng)度、階數(shù)的變化會(huì)產(chǎn)生廣義共振;而當(dāng)階數(shù)固定時(shí),粒子鏈的平均流速則會(huì)隨噪聲強(qiáng)度的變化出現(xiàn)廣義隨機(jī)共振現(xiàn)象.

2 模型建立

2.1 經(jīng)典的FK模型

考慮經(jīng)典的FK模型[16,17],如圖1所示,周期長(zhǎng)為l的棘齒勢(shì)V(x),在外力yi(t)和噪聲的驅(qū)動(dòng)下,忽略慣性效應(yīng),系統(tǒng)運(yùn)動(dòng)方程為

其中k為耦合強(qiáng)度,D為噪聲強(qiáng)度,設(shè)粒子間自由長(zhǎng)度為a,不顯含于上式,γ為阻尼系數(shù),為方便通常設(shè) γ=1,ξi(t)為高斯白噪聲:〈ξi(t)〉=0,

圖1 FK模型原理圖

2.2 分?jǐn)?shù)階FK模型

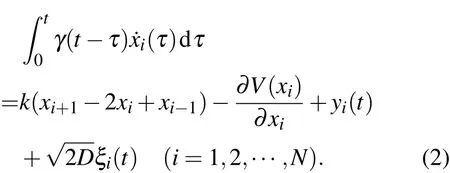
然而在很多物理和生化環(huán)境中,黏性介質(zhì)對(duì)速度通常具有冪律記憶性:距當(dāng)前時(shí)刻越近,記憶性越強(qiáng);距當(dāng)前時(shí)刻越遠(yuǎn),記憶性越差.描述這種退色記憶性的阻尼核函數(shù)γ(t)為[21]

為方便通常設(shè)γ0=1.

由圖2可以看出,γ(t)隨著時(shí)間t的增加按t的冪次逐漸衰減,α越大γ(t)衰減越快,α越小γ(t)衰減越慢.

把(3)式帶入(2)式得到

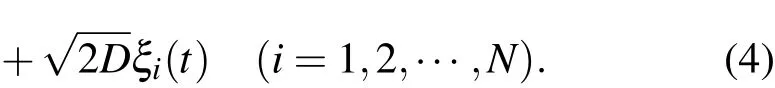
根據(jù)Caputo分?jǐn)?shù)階微積分的定義[22,23],上式可以寫為

稱(5)式為分?jǐn)?shù)階FK模型.

圖2 分?jǐn)?shù)階阻尼核函數(shù)γ(t)

2.3 模型說(shuō)明

這里所關(guān)心的重點(diǎn)是耦合系統(tǒng)粒子鏈的平均流速[5],定義如下:

其中N是系統(tǒng)中的粒子數(shù),T為總時(shí)間.平均流速是一個(gè)宏觀物理量,反映了粒子運(yùn)動(dòng)的一個(gè)整體趨勢(shì).

圖3 勢(shì)函數(shù)V(x)示意圖

我們選用一個(gè)周期l=1的棘輪勢(shì),形式為

V(x)的示意圖如圖3.

對(duì)外力yi(t),要求滿足〈yi(t)〉=0,即外力無(wú)偏置.這里主要考慮yi(t)為對(duì)稱的周期力

其中A為周期力幅度,ω為周期力的角頻率.

3 數(shù)值模擬

當(dāng)粒子間沒有相互作用,即k=0時(shí),系統(tǒng)轉(zhuǎn)化為外力作用下的單粒子在棘輪勢(shì)中的運(yùn)動(dòng);當(dāng)粒子間相互作用趨于無(wú)窮大,即k→∞時(shí),所有粒子都被剛性束縛在一起,系統(tǒng)的動(dòng)力學(xué)行為相當(dāng)于單個(gè)粒子在有效勢(shì)中的運(yùn)動(dòng)[5].本文排除上述極端情況,主要考慮對(duì)于有限大小的耦合強(qiáng)度k,粒子間的相互作用所引起的復(fù)雜定向輸運(yùn)行為.

為了模擬方程(5)所刻畫的粒子運(yùn)動(dòng),我們采用分?jǐn)?shù)階差分法[22].采樣步長(zhǎng)?t=0.005 s,仿真時(shí)間取50 s,粒子數(shù)N=10,角頻率ω=1,噪聲強(qiáng)度D=0.1,采用周期邊界.

需要指出的是,粒子xi在時(shí)刻t受到的阻尼力即t時(shí)刻的阻尼力是時(shí)段[0,t]內(nèi)的速度關(guān)于阻尼核γ(t)的加權(quán)平均.當(dāng)階數(shù)α→1時(shí),即系統(tǒng)的記憶性變差,核函數(shù)γ(t)的衰減加快,這意味著歷史速度對(duì)當(dāng)前阻尼力貢獻(xiàn)減少,阻尼力變?nèi)?導(dǎo)致粒子具有更快的輸運(yùn)速度;而當(dāng)階數(shù)α降低時(shí),即系統(tǒng)的記憶性增強(qiáng),歷史速度對(duì)當(dāng)前阻尼力貢獻(xiàn)增強(qiáng),阻尼力也隨之增強(qiáng),致使定向輸運(yùn)的速度減緩,甚至當(dāng)這種記憶性增強(qiáng)到某一程度時(shí),促使粒子反向越過勢(shì)壘,形成定向輸運(yùn)反向流.

對(duì)不同強(qiáng)度的周期力和不同大小的耦合強(qiáng)度,圖4給出了平均流速v與階數(shù)α的關(guān)系.

圖4 不同耦合強(qiáng)度和周期力幅度下,粒子鏈平均流速v與階數(shù)α的關(guān)系 (a)k=0;(b)k=3;(c)k=5;(d)k=10

在周期力強(qiáng)度較弱時(shí)(A=0,1),小周期力不足以使得單個(gè)粒子越過勢(shì)壘,粒子只能在勢(shì)阱中徘徊.當(dāng)粒子間不存在相互作用,即k=0時(shí),眾粒子的運(yùn)動(dòng)不能相互協(xié)調(diào),各粒子在時(shí)刻t所受阻尼力的方向也不盡相同,即使較小的階數(shù)α導(dǎo)致歷史速度對(duì)當(dāng)前阻尼力貢獻(xiàn)較強(qiáng),也不足以使得單個(gè)粒子越過勢(shì)壘形成定向輸運(yùn);但若粒子間存在相互作用,即k＞0時(shí),耦合使得粒子間的運(yùn)動(dòng)相互協(xié)調(diào),各粒子在時(shí)刻t所受阻尼力也就具有較大的同向分量,加之小周期力和噪聲的作用,這樣當(dāng)階數(shù)足夠小時(shí),粒子鏈將形成定向輸運(yùn)反向流.

在受到較強(qiáng)的周期力時(shí),周期力能促使單個(gè)粒子越過勢(shì)壘.我們觀察到,若階數(shù)α→1時(shí),系統(tǒng)的記憶性變差,有正的定向流出現(xiàn);但當(dāng)α→α0(α0為v(α)與橫坐標(biāo)交點(diǎn)所對(duì)應(yīng)的階數(shù),參見圖4)時(shí),系統(tǒng)的記憶性增強(qiáng)導(dǎo)致粒子運(yùn)動(dòng)的阻尼力增強(qiáng),平均流速v將減小并趨于0;隨著階數(shù)α繼續(xù)減小,將會(huì)出現(xiàn)定向輸運(yùn)反向流,并在負(fù)方向上出現(xiàn)一個(gè)共振峰值.對(duì)于不同的周期力強(qiáng)度,發(fā)現(xiàn)在A=5的時(shí)候,對(duì)應(yīng)著較大的正向平均流速,說(shuō)明系統(tǒng)在階數(shù)和耦合強(qiáng)度固定時(shí),存在一個(gè)使粒子鏈平均流速極大的A.并且對(duì)于具有較大正向平均流速的A,要使系統(tǒng)出現(xiàn)定向輸運(yùn)反向流的阻尼力也應(yīng)較大,因此對(duì)阻尼力有實(shí)質(zhì)貢獻(xiàn)的歷史時(shí)間需要更長(zhǎng),也就是對(duì)應(yīng)于更小的α0;而當(dāng)周期力幅度A相同時(shí),隨著耦合強(qiáng)度k的增加,α0也增加.

對(duì)不同的階數(shù)α,圖5給出了周期力幅度A=2.3時(shí),平均流速v與耦合強(qiáng)度k的關(guān)系.當(dāng)α=1和0.8時(shí),可以明顯觀察到正向上的共振曲線,即在某一優(yōu)化耦合強(qiáng)度下系統(tǒng)存在正向極大平均流速.隨著階數(shù)下降到0.5,系統(tǒng)記憶性增強(qiáng),系統(tǒng)產(chǎn)生了反向流,并隨k增加,在負(fù)向上出現(xiàn)了共振曲線,即在k≈3時(shí),粒子鏈存在負(fù)向極大平均流速.這組曲線表明:太弱的耦合不能使得粒子之間形成統(tǒng)一的躍遷;太強(qiáng)的耦合,所有粒子束縛在一起,同樣限制了粒子鏈的輸運(yùn);適當(dāng)?shù)鸟詈蠌?qiáng)度可以使粒子鏈的輸運(yùn)速度達(dá)到極值.

圖5 不同階數(shù)下,粒子鏈平均流速v與耦合強(qiáng)度k的關(guān)系 (a)α=1.0;(b)α=0.8;(c)α=0.5

圖6 階數(shù)固定情況下,輸運(yùn)速度v與噪聲強(qiáng)度D關(guān)系

圖7 不同階數(shù)下,各粒子平均位移隨時(shí)間的演化 (a)α=0.6;(b)α=0.8

固定A=1.6,k=3,圖6展示了平均流速v與噪聲強(qiáng)度D的關(guān)系.我們發(fā)現(xiàn)當(dāng)階數(shù)為1時(shí),系統(tǒng)不具有記憶性,平均流速v在正向上產(chǎn)生了廣義隨機(jī)共振現(xiàn)象.當(dāng)α=0.8時(shí),系統(tǒng)記憶性較弱,觀察到了與整數(shù)階情況相同的現(xiàn)象,但在噪聲強(qiáng)度較弱的時(shí)候(D＜8),平均流速明顯快于整數(shù)階情況,這主要是由于在具有記憶性的系統(tǒng)中,歷史速度對(duì)當(dāng)前阻尼力有貢獻(xiàn),而歷史速度受到歷史噪聲的影響,因此歷史噪聲間接地對(duì)當(dāng)前速度做出貢獻(xiàn),所以較之整數(shù)階情況,達(dá)到極大平均流速所需要的噪聲強(qiáng)度明顯下降.而當(dāng)階數(shù)減少到0.6時(shí),系統(tǒng)記憶性再增強(qiáng),平均流速v隨噪聲強(qiáng)度D的增加在負(fù)向上產(chǎn)生了廣義隨機(jī)共振現(xiàn)象.

固定噪聲強(qiáng)度D=5,圖7給出α分別為0.6及0.8時(shí),各粒子平均位移〈xi(t)〉的時(shí)間演化.可以明顯地看出,當(dāng)α=0.6時(shí)粒子整體向負(fù)方向運(yùn)動(dòng),而α=0.8時(shí)粒子整體向正方向運(yùn)動(dòng).這同樣證實(shí)了前文的結(jié)論:分?jǐn)?shù)階的階數(shù),即系統(tǒng)的記憶性,對(duì)粒子鏈的運(yùn)動(dòng)方向有顯著影響.

4 結(jié)論

本文主要研究了粒子鏈在階數(shù)和其他參數(shù)相互作用下的復(fù)雜輸運(yùn)現(xiàn)象.得到以下結(jié)論:1)系統(tǒng)的記憶性即系統(tǒng)的階數(shù)對(duì)粒子鏈的運(yùn)動(dòng)狀態(tài)有顯著影響,在固定其他參數(shù)時(shí),調(diào)節(jié)階數(shù)將導(dǎo)致粒子鏈出現(xiàn)定向輸運(yùn)反向流,并在某一階數(shù)產(chǎn)生隨機(jī)共振;2)不同階數(shù)的噪聲-平均流速曲線v(D)表明,分?jǐn)?shù)階系統(tǒng)出現(xiàn)極大平均流速所需的噪聲強(qiáng)度較之整數(shù)階系統(tǒng)更小;并且在小噪聲狀態(tài)下,平均流速明顯快于整數(shù)階系統(tǒng);3)當(dāng)階數(shù)固定時(shí),耦合強(qiáng)度-平均流速曲線v(k)表明,平均流速會(huì)隨耦合強(qiáng)度的變化出現(xiàn)廣義共振,當(dāng)階數(shù)較大即系統(tǒng)記憶性較弱時(shí),出現(xiàn)正向粒子流的廣義共振,而當(dāng)階數(shù)較小即系統(tǒng)記憶性較強(qiáng)時(shí),則出現(xiàn)反向粒子流的廣義共振.

[1]H¨anggi P,Marchesoni F 2009 Rev.Mod.Phys.81 387

[2]Qian M,Wang Y,Zhang X J 2003 Chin.Phys.Lett.20 810

[3]Ai B Q,He Y F 2010 J.Chem.Phys.132 094504

[4]Wang H Y,Bao J D 2004 Physica A 337 13

[5]Csah′ok Z,Family F,Vicsek T 1997 Phys.Rev.E 55 5179

[6]Ai B Q,He Y F,Zhong WR 2011 Phys.Rev.E 83 051106

[7]Kumar K V,Ramaswamy S,Rao M 2008 Phys.Rev.E 77 020102

[8]Gehlen S V,Evstigneev M,Reimann P 2009 Phys.Rev.E 79 031114

[9]Fendrik A J,Romanelli L 2012 Phys.Rev.E 85 041149

[10]Zheng Z G 2004 Spatiotemporal Dynamics and Collective Behaviors in Coupled Nonlinear Systems(Beijing:Higher Education Press)p279(in Chinese)[鄭志剛2004耦合非線性系統(tǒng)的時(shí)空動(dòng)力學(xué)與合作行為(北京:高等教育出版社)第279頁(yè)]

[11]Vadakkepatt A,Dong Y L,Lichter S,Martini A 2011 Phys.Rev.E 84 066311

[12]Nishikawa M,Takagi H,Shibata T,Iwane A H,Yanagida T 2008 Phys.Rev.Lett.101 128103

[13]Camp`as O,Kafri Y,Zeldovich K B,Casademunt J,Joanny J F 2006 Phys.Rev.Lett.97 038101

[14]Liu F,Anh V V,Turner I,Zhuang P 2003 J.Appl.Math.Comp.13 233

[15]de Andrade M F,Lenzi E K,Evangelista L R,Mendes R S,Malacarne L C 2005 Phys.Lett.A 347 160

[16]Braun O M,Kivshar Y S 2004 The Frenkel-Kontorova Model:Concepts,Methods and Application(New York:Springer)

[17]Han X Q,Jiang H,Shi Y R,Liu Y X,Sun J H,Chen J M,Duan W S 2011 Acta Phys.Sin.60 116801(in Chinese)[韓秀琴,姜虹,石玉仁,劉妍秀,孫建華,陳建敏,段文山2011物理學(xué)報(bào)60 116801]

[18]Bao J D 2009 Random Simulation Method of Classical and Quantum Dissipation System(Beijing:Science Press)p80(in Chinese)[包景東2009經(jīng)典和量子耗散系統(tǒng)的隨機(jī)模擬方法(北京:科學(xué)出版社)第80頁(yè)]

[19]Oldham K B,Spanier J 1974 The Fractional Calculus(New York:Academic Press)

[20]Kou S C,Xie X S 2004 Phys.Rev.Lett.93 180603

[21]Gao S L,Zhong S C,Wei K,Ma H 2012 Acta Phys.Sin.61 100502(in Chinese)[高仕龍,鐘蘇川,韋鹍,馬洪2012物理學(xué)報(bào)61 100502]

[22]Podlubny I 1999 Fractional Differential Equations(San Diegop,CA:Academic Press)

[23]Samko S G,Kilbas A A,Marichev O I 1993 Fractional Integrals and Derivatives Theory and Applications(New York:Gordon and Breach Science Publisher)