基于實數編碼量子進化算法的IIR數字濾波器優化設計

哈爾濱電氣集團阿城繼電器有限責任公司 孫成發

1.引言

IIR數字濾波器是一類重要的濾波器，具有較高的計算精度，且能夠用較低的階數獲得很好的頻率選擇特性，已在很多領域得到了應用。IIR數字濾波器設計是信號處理中的一個重要課題。許多學者在IIR數字濾波器設計方面作了大量的工作[1-4]，主要分為兩類：一類是先設計模擬濾波器，然后利用雙線性變換轉變為數字濾波器，方法簡單易行，但設計結果有時不是十分理想[1]；另一類是基于某一優化準則，將數字濾波器設計問題轉化為優化問題的求解，以使設計的數字濾波器性能達到最優，但由于相應的優化問題均是復雜的多參數非線性函數優化問題，在求解過程中極易陷入局部極值，難以得到全局最優解或滿意解。近年來，隨著智能優化算法的發展，已有學者將遺傳算法（GA）[2]和粒子群算法（PSO）[3，4]應用到IIR是字濾波器設計中，但GA算法存在著難以克服的“早熟”和“停滯”問題；PSO雖然運行速度快，簡單，但仍有很大可能陷入局部極值。

實數編碼量子進化算法（Read-coded quantum evolutionary algorithms，RQEA）是基于量子計算的相關概念和原理形成的一種概率性搜索算法，具有收斂速度快，全局搜索能力強的特點[5，6]。RQEA為數字濾波器的設計提供了一種新的工具，文中將RQEA用于IIR數字濾波器的優化設計，給出了IIR數字濾波器設計的優化模型，介紹了RQEA的基本原理和應用RQEA設計IIR數字濾波器的具體實現過程，最后，通過仿真試驗表明應用RQEA設計IIR數字濾波器不僅可行，而且有效。

2.IIR數字濾波器優化設計

2.1 IIR濾波器的優化模型

設N階IIR數字濾波器的傳遞函數描述為：

如采用(1)式進行IIR數字濾波器設計，則待優化參數共有M +N+2個，且各參數的取值范圍難以確定。為了便于采用優化算法進行IIR數字濾波器優化設計，通常采用二階節的級聯結構形式對(1)式進行變形，即：

式中A是增益，是一個常數，N為二階節的個數，ak、bk、ck和dk是待優化設計參數。當IIR濾波器采用(2)式結構時，頻率響應對系數變化的敏感度低，便于調整頻率響應。(2)式對應的IIR數字濾波器的頻率響應為：

式中：

2.2 參數取值范圍的確定

將(3)式代入(5)式得：

可見，E是增益A和濾波器系數ak、bk、ck和dk(N k=1,…,)的非線性函數，而增益A不是獨立參數，可由其它參數參數確定，則優化問題（5）式含有4k個參數。

將(6)式對A求微分并令其為0，可推導出最佳增益A的解析表達式，即：

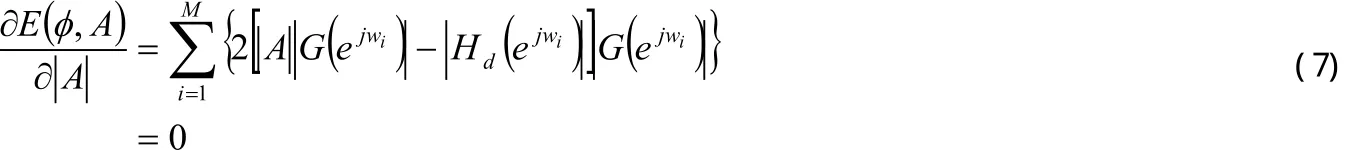
可得：

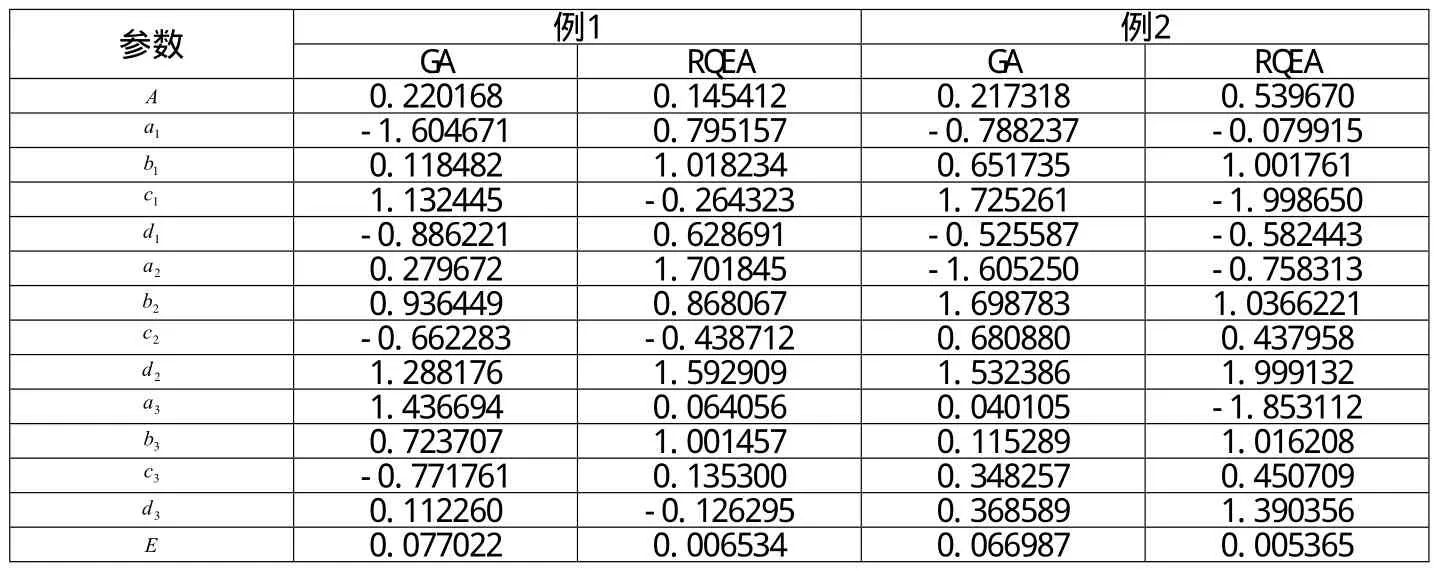
表1 IIR數字濾波器設計結果Table1 Results of IIR digital filter design

圖1 不同算法進化過程Fig.1 Evolutionary procures of different algorithms

由于只考慮幅度響應誤差，A的正負值對結果沒有影響。但是，為了保證設計濾波器的穩定性，需要對優化參數范圍進行限制。由(2)式可知，只要使每個二階節的極點都在Z平面的單位園內，即：的零點zk都滿足由此可以確定ck和dk的取值范圍為：-2＜ck＜2，-1＜dk＜1，(k=1,…,N )。若參數在此范圍內取值，優化結果仍然出現不穩定極點，可以用該極點在單位圓內的映像代替該極點(相當于級聯了一個全通網絡)，可以在不改變濾波器幅頻響應的基礎上，保證得到穩定的濾波器。如果要求設計的濾波器同時具有最小相移特性，對ak和bk的取值范圍作同樣的限制。

3.實數編碼量子進化算法(RQEA)

RQEA基本思想[5]：(1)構造實數編碼三倍體染色體；(2)利用量子旋轉門和基于高斯變異的互補雙變異算子一起進化染色體；(3)通過離散交叉實現染色體之間的信息交流，擴大算法搜索范圍；(4)采用“爬山”選擇，加快算法收斂速度。

實數編碼三倍體染色體的等位基因由復雜函數自變量向量x的一個分量xi和量子比特的一對概率幅組成，即：，則實數編碼三倍體染色體可描述為：

式中，αi和βi滿足歸一化條件，i=1,…,n。n為染色體長度，由復雜函數的維數決定。

RQEA對每一個染色體實施單基因變異[7]。設第t代時群體為N為群體規模。對于，隨機選擇第i基因位對變量進行高斯變異，可得：

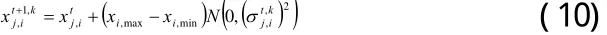
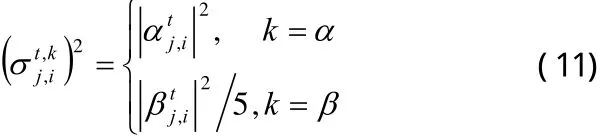
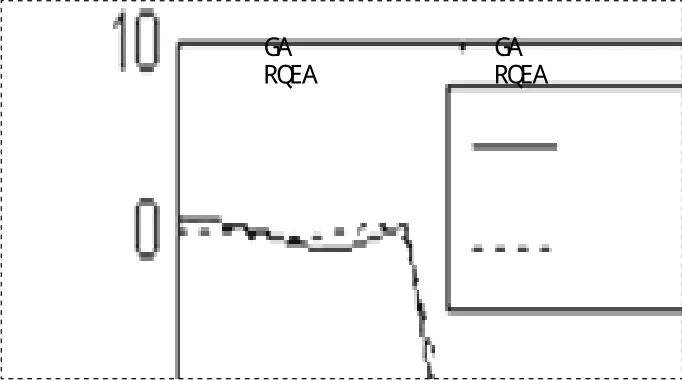
圖2 不同算法設計濾波器幅頻特性Fig.2 Magnitude of filter designed by different algorithms

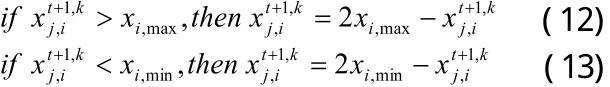
若由(10)式生成的新染色體優于原染色體，則為有效進化，可令否則為無效進化，并由量子旋轉門更新和，即：

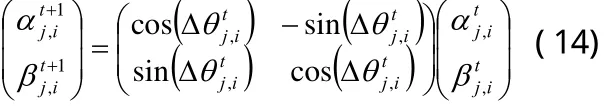
式中，θ0為初始旋轉角，γ為進化尺度，θ0和γ控制旋轉角大小；符號函數sgn（·）控制旋轉角方向，以確保算法收斂。

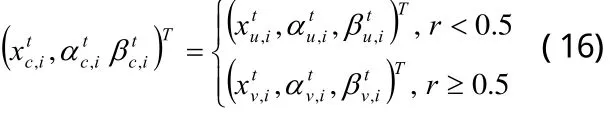
4.算例分析

為了驗證文中提出方法的有效性和優越性，采用RQEA設計低通濾波器（例1）和高通濾波器（例2），同時，出于比較的目的，采用GA求解相同的問題。

例1：設計一個低通濾波器，其技術指標為：

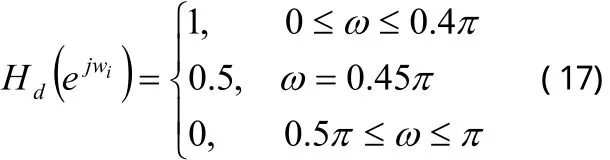
例2：設計一個高通濾波器，其技術指標為：

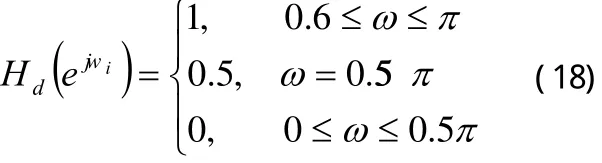
在例1和例2中，數字濾波器均選用3個二階節，即N=3，則濾波器參數共有個，頻域采樣點數均取為21。RQEA相關參數為：群體規模、初始旋轉角θ0=0.3π、進化尺度、實數編碼三倍體染色體基因位中的概率幅均取為連續“求精”和“求泛”次數分別為mf=6，mc=2；GA相關參數為：群體規模，是RQEA群體規模的2倍，最優個體保留，蒙特卡羅選擇，交叉概率pc=0.7，變異概率pm=0.1。兩種算法均以運算代數作為終止條件，且運算代數取為500，為消除單次運算存在的偶然性，各種算法均在給定參數下獨立運算10次，取其中最好的一次作為最終優化結果。圖1描述了設計數字濾波器的優化過程。圖2描述了設計數字濾波器的幅頻特性。

由圖1可以看出，RQEA無論是收斂速度，還是優化結果均優于GA。由圖2不難發現，應用RQEA設計的數字濾波器的通帶波動、過度帶斜率以及阻帶衰減均要優于GA設計的數字濾波器，應用RQEA設計數字濾波器具有更好的綜合性能。表1列出了數字濾波器設計結果，濾波器各個參數均保留6位小數，能夠發現RQEA設計數字濾波器與理想濾波器的均方誤差更小，性能更優。

5.結論

鑒于IIR數字濾波器優化設計本質上是一個多維非線性函數優化問題，文中將具有全局收斂性好，收斂速度快特點的RQEA引入IIR數字濾波器設計中。仿真實驗表明，應用RQEA優化設計IIR數字濾波器較GA具有更優良的性能，具有實際意義。

[1]Deckey A G.Synthesis of Recursive Digital Filters Using the minimum P-error Criterion[J].IEEE Trans.Audio Electroacoust,1972,20:257-263.

[2]李建華,殷福亮.設計IIR數字濾波器的遺傳優化算法[J].通信學報,1999,17(3):1-7.

[3]侯志榮,呂振肅.IIR數字濾波器設計的例子群優化算法[J].電路與系統學報,2003,8(4):16-19.

[4]張松華,陸秀令.IIR數字濾波器的粒子群優化設計方法[J].信息與電子工程,2007,5(4):271-274.

[5]高輝,徐光輝,張銳,等.實數編碼量子進化算法[J].控制與決策,2008,23(1):87-90.

[6]Gao H,Zhang R.Real-coded quantum evolutionary algorithm for global namerical optimization with continuous variables.Chinese Journal of Electronics(CJE),2011,20(3):499-503.

[7]王湘中,喻壽益.適用于高維優化問題的改進進化策略[J].控制理論與應用,2006,23(1):148-151.