CNS/SINS組合導航系統仿真分析

黃志遠，黃聲享

（武漢大學 測繪學院，湖北 武漢 430072）

隨著組合導航技術的發展，基于慣性導航和天文導航的組合導航系統成為導航等領域研究的熱點之一。慣性導航和天文導航都是自主式導航系統，前者不依賴于外部信息，可提供包括速度、位置、姿態在內的全導航參數，相對精度較高，但由于定位誤差隨時間積累，難以作為獨立的高精度導航系統使用［1］；后者的誤差不隨時間增加而累積，并能夠提供最高精度的姿態參數，但是卻受到外界條件的限制。因此，兩個系統的相互組合，可以達到提高導航性能的目的。

本文以彈道導彈為設計對象，首先通過軌跡發生器模擬導彈飛行姿態，然后在慣性系下建立天文導航和捷聯慣性導航（CNS/SINS）組合導航的數學模型，并設計了離散型卡爾曼濾波功能，最后通過對SINS和CNS/SINS的仿真比較，驗證CNS/SINS組合導航系統的可靠性。

1 CNS/SINS組合導航數學模型

CNS/SINS組合導航系統的數學模型主要包括狀態方程和量測方程兩個方面。

1.1 狀態方程

對彈道導彈而言，在綜合考慮加速度誤差、速度誤差、位置誤差和數學平臺角誤差之后，取15維狀態變量的狀態方程為［2－4］

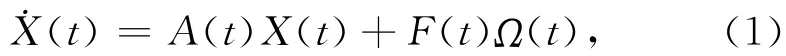
其系統變量X（t）為

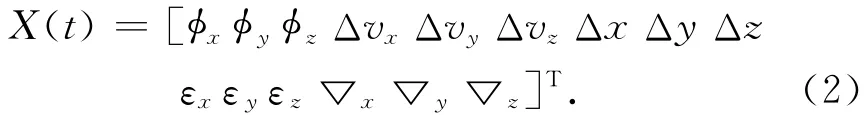
式中：φx、φy、φz是3個數學平臺失準角；Δvx、Δvy、Δvz是起點在慣性系3個坐標軸上的3個速度誤差；Δx、Δy、Δz是3個位置誤差；εx、εy、εz是3個陀螺儀常值漂移；▽x、▽y、▽z是3個加速度計常值漂移。

而系統噪聲Ω（t）的表達形式為

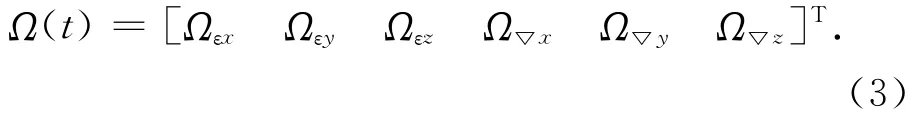
其中前3項是陀螺儀高斯白噪聲；后3項是加速度計高斯白噪聲。而系統的噪聲方差陣為［4］

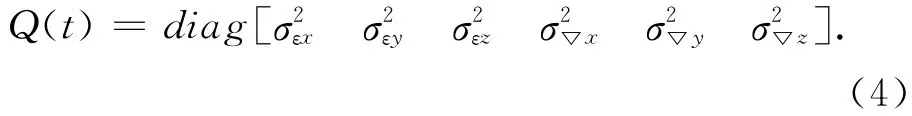
在狀態方程中的系數陣A（t）和F（t）的表達形式為

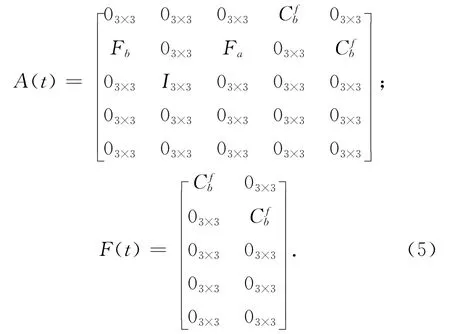
式中：Fa是由引力加速度對位置坐標的偏導數；Fb是由視加速度構成的反對稱陣；Cfb是載體系到起點慣性坐標系的姿態轉換陣。

1.2 量測方程

利用導航坐標系下的數學平臺誤差角方程形成的CNS/SINS組合系統的量測方程為［2，4］

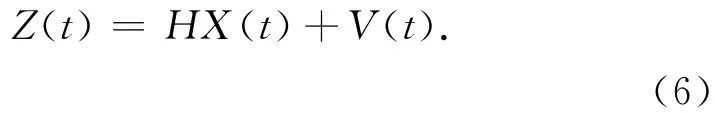
式中：H＝［I3×303×12］；V（t）是CNS零均值測量白噪聲。

CNS/SINS組合導航系統只能獲得姿態誤差角的觀測量，而導航狀態方程中包含的卻是數學平臺失準角，為此需要知道姿態誤差角到數學平臺失準角的變換矩陣，才能將姿態誤差角作為觀測值用于導航濾波。

定義四元數誤差Δq＝qi－（i＝0，1，2，3）。其中，qi是由CNS輸出的四元數理想值，是SINS輸出的姿態四元數實際估計值。那么采用四元數形式的姿態誤差角與數學平臺失準角之間的轉換關系如下［5］：

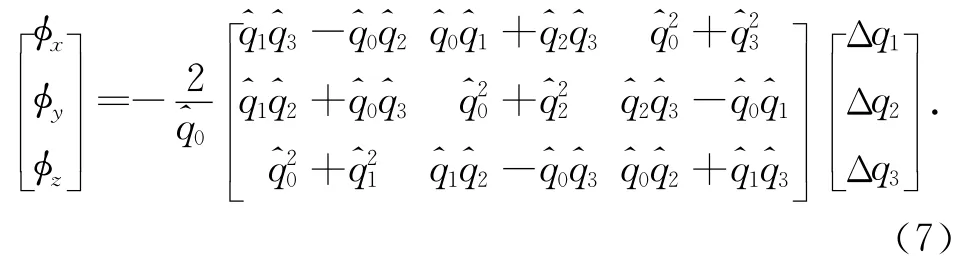
2 離散型卡爾曼濾波

根據實際需要，可以將組合導航狀態方程離散化為［3］

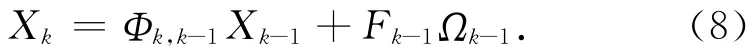
式中：Φk，k－1為k－1時刻到k時刻的一步狀態轉移矩陣。對Xk的量測滿足量測方程Zk＝HkXk＋Vk。由此離散型卡爾曼濾波的基本方程可以表示為公式（9）～（13）的形式［4］。

狀態一步預測

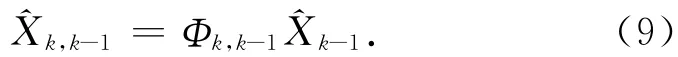
狀態估計

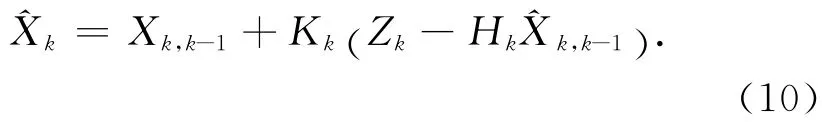
濾波增益

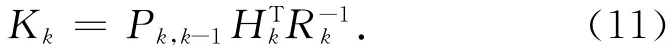
一步預測均方誤差

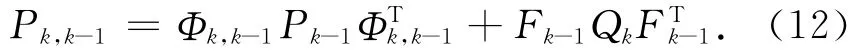
估計均方誤差

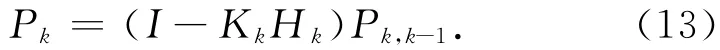
3 系統仿真及結果分析

在組合導航研究方面，更多的都是基于組合導航算法的研究［6］。為此，本文采用MATLAB進行程序設計，模擬彈道導彈的發射過程，對SINS和CNS/SINS仿真比較，驗證CNS/SINS組合導航系統的可靠性。

3.1 仿真參數設置

假設彈道導彈發射方位角為90°，初始姿態的俯仰角為90°，推力加速度為30m/s2，航向角和滾動角均為0°，導彈垂直發射上升時間為20s，主動段轉彎結束時刻為50s，發動機關機時間為150s。仿真參數見表1。

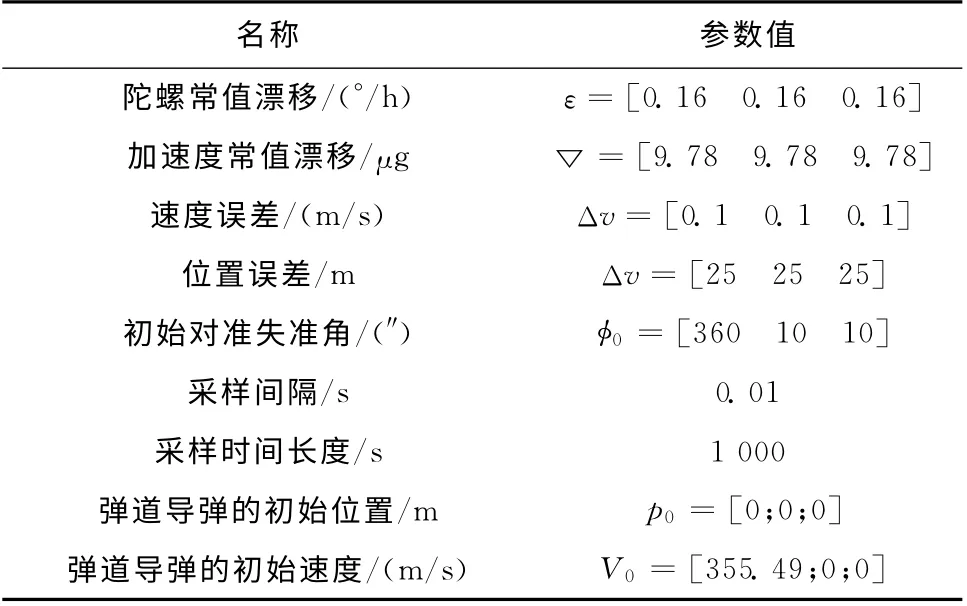
表1 仿真參數

3.2 仿真分析

彈道導彈遠距離、彈道高、時速快的飛行特點對導航系統提出很高的技術要求［6］。圖1顯示了在慣性系下的彈道導彈理論彈道、單純采用SINS解算的彈道以及CNS/SINS組合導航解算的彈道的三維軌跡。從圖中看出：SINS條件下導彈三軸位置誤差隨時間不斷增加。采用CNS/SINS組合導航解算的導彈彈道更接近理論彈道值。

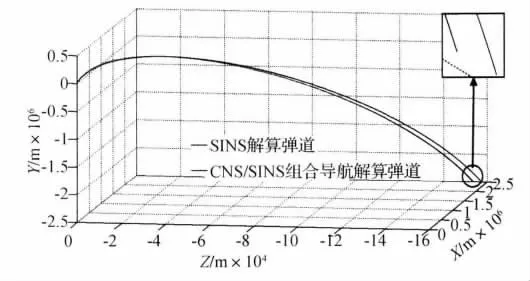
圖1 導彈理論彈道與導航解算彈道

3.2.1 位置誤差

圖2顯示了分別采用SINS和SINS/CNS組合導航解算的導彈三軸位置誤差。由于陀螺漂移、加速度計漂移的誤差、初始失準角的影響，仿真結束時，SINS解算的結果表明X軸向位置誤差為－309.1m，Y軸向位置誤差為2 070m，Z軸向位置誤差為－3 826m，且誤差隨著飛行時間的增加而有增加的趨勢。然而，CNS/SINS組合導航系統可以提高對位置的解算精度。在采用組合導航系統后，導彈的X軸向位置誤差為－171.2m，Y軸向位置誤差為242.4m，Z軸向誤差為－278.8m，且誤差隨著時間的增加變化較為平穩。

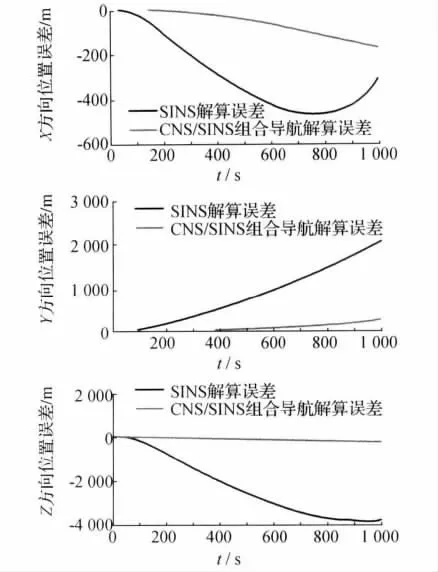
圖2 SINS和CNS/SINS解算的導彈三軸位置誤差

3.2.2 速度誤差

圖3顯示了分別采用SINS和SINS/CNS組合導航解算的導彈三軸速度誤差，結果表明：SINS解算的導彈X，Y，Z3個方向速度存在著較大的誤差，到仿真結束時，X軸向速度誤差為1.694m/s且最大；Y軸向速度誤差為3.277m/s且最大；Z軸向位置誤差為1.582m/s，而最大值是發動機關機時刻150s時的－6.583m/s，在整個仿真過程中，由于前150s存在發動機的推動作用，速度誤差隨著飛行時間的增加而不斷增加，150s時速度誤差出現轉折點。CNS/SINS組合導航系統可以提高對速度的解算精度。在采用組合導航系統后，導彈的X軸向位置 誤 差 為－0.198 4m/s，Y軸 向 位 置 誤 差 為0.613 8m/s，Z軸向誤差為－0.414m/s，且誤差隨著時間的增加變化較為平穩。

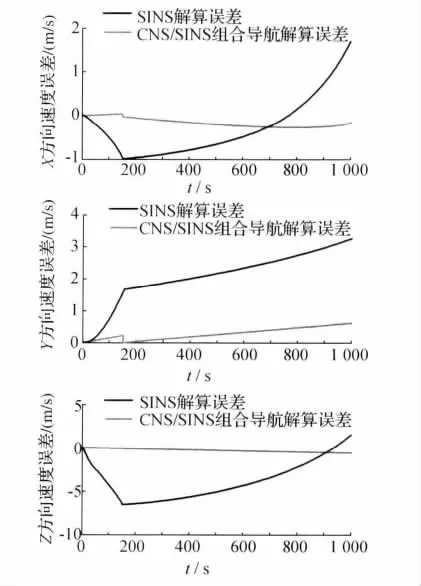
圖3 SINS和CNS/SINS解算的導彈三軸速度誤差

3.2.3 姿態角誤差

由圖4可見，采用SINS解算的姿態角誤差隨時間的增加呈現增加的趨勢，即SINS解算姿態角的精度較低。而CNS/SINS解算的姿態角誤差維持在零的水平，說明組合導航對提高姿態角解算精度有很大的幫助。

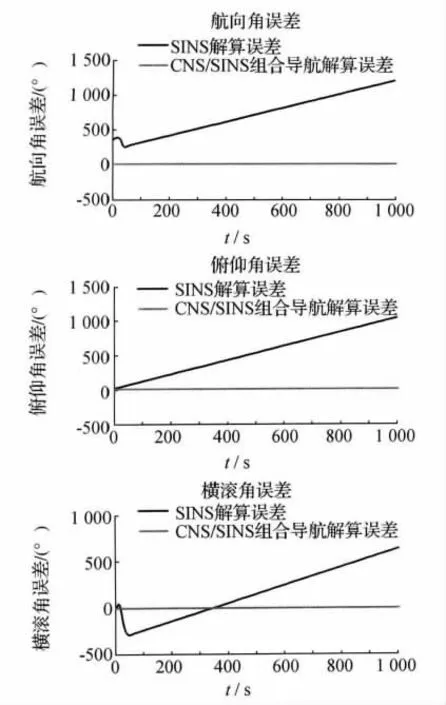
圖4 SINS和CNS/SINS解算的導彈姿態角誤差

4 結束語

天文導航和捷聯慣性導航（CNS/SINS）是優勢互補的組合導航系統，通過對速度誤差、位置誤差、姿態角的高精度解算，再結合適當的修正方案可實現高精度導航。利用MATLAB軟件對組合導航的仿真結果說明CNS/SINS綜合利用了兩個系統的測量信息，能夠對位置誤差、速度誤差進行有效估計，提高導航精度，而且還能對姿態角進行有效估計，為導彈的制導提供依據。

［1］王安國.現代天文導航及其關鍵技術［J］.電子學報，2007，35（12）：2347－2353.

［2］鄧紅，劉光斌，陳昊明，等.彈道導彈捷聯慣導/衛星系統/天文系統組合導航研究［J］.導彈與航天運載技術，2004（2）：24－28.

［3］崔希璋，於宗儔，陶本藻，等.廣義測量平差［M］.2版.武漢：武漢大學出版社，2009：220.

［4］房建成，寧曉琳.天文導航原理及應用［M］.北京：北京航空航天大學出版社，2006：151－278.

［5］鄧紅，劉光斌，陳昊明，等.發射慣性坐標系下誤差角與數學平臺失準角的推導與仿真［J］.宇航學報，2011，32（4）：781－786.

［6］張通，張駿.彈道導彈慣性/雙星/天文組合導航系統研究［J］.計算機仿真，2009，26（3）：40－42.

［7］吳太旗，孫付平，易維勇，等.GPS/INS組合導航系統的MATLAB/Simulink仿真［J］.測繪學院學報，2004，21（3）：172－174.