碰靠定位算法在不規則件排樣優化中的應用研究

梁利東 鐘相強

安徽工程大學，蕪湖，241000

0 引言

排樣是指將原材料分割成不同形狀的零件毛坯，因此排樣問題可抽象為在給定規格的原材料(如板材)中，尋找零件排放最優布局的優化問題。不規則件排樣屬于最復雜的組合優化問題之一，不僅表現在對不規則零件圖形的幾何形狀描述，還表現在零件形狀不規則性將導致零件之間的靠接、判交、控制和評價等處理比較復雜且計算量大。

對于不規則零件排樣問題，無論是采用矩形化包絡法［1］，還是對不規則零件直接排樣如臨界多邊形法［2-3］等，都需要對零件圖形進行判交和碰靠定位處理，以實現零件之間的緊密靠接來提高原材料的利用率。文獻［1］中提出了一種典型的不規則排樣算法，即將不規則件以矩形件排樣結束后，對每個零件進行試探性的移動碰靠測試，通過壓縮或擠壓過程來減少未利用空間。Hopper等［4］指出了該算法的局限性，因為單個零件的移動可能會導致其他零件的排樣位置發生變化，從而難以確定零件的移動方向并影響了計算效率。文獻［5］提出的柵格表示法是將板材劃分為大小相同的矩形柵格或網格，用它來近似地表示零件的輪廓特征，同時通過判斷兩個零件圖形所占的柵格狀態來判斷零件間的位置關系，算法實現簡單。但這種離散化的表示方法受零件圖形的特征或精度要求的局限，對于那些帶有復雜弧度或曲線的零件，當需要得到較高的排樣精度時，會使得柵格數量劇增，計算量也相應增加，降低了算法的效率。文獻［6］在臨界多邊形(NFP)算法的基礎上，提出了重心NFP的概念，通過零件的旋轉和移動選擇重心NFP中最低重心位置來確定零件的排放定位。這種方法在求解過程中基本上實現了零件最低的定位原則，但需要考慮已排零件與邊界形成的輪廓以用來求解NFP的移動碰靠軌跡，計算量較大。

針對以上方法的優劣分析，本文在對每個入排零件進行矩形化預處理來確定其初始位置的基礎上，根據最小靜矩原理對零件圖形進行旋轉和移動碰靠來搜索當前零件的最佳排放位置，并以其排樣高度和碰靠距離來評價最佳吻合定位，從而實現即時多角度碰靠優化。

1 碰靠定位算法原理

1.1 最低形心碰靠定位方法

零件的排放姿態涉及入排角度的確定，本文采用的最小靜矩碰靠定位方法是在保證整體排樣高度不增加的基礎上，盡可能通過對零件多邊形的旋轉和平移碰靠處理，使零件多邊形的靜矩最小。靜矩的物理意義表示零件圖形相對于板材邊界的遠近程度或零件之間距離的大小，對于排樣問題，選擇其最小靜矩的入排角度進行排放，從理論上可增加零件與板材邊界及零件與零件的接觸面，以減少排樣過程形成的無效區域，從而增加板材的利用率。圖1表示了不同零件在排放中的一般定位(上兩個示圖)和最小靜矩定位(下兩個示圖)的對比示意。圖中的兩組示圖分別以矩形件和不規則零件為例說明，可見零件在入排過程中以最小靜矩碰靠進行定位能有效提高排樣區域的有效利用率。特別指出，最小靜矩碰靠定位方法是:通過對每個入排零件圖形相對于形心的多次旋轉及定位碰靠試算，從中選擇出靜矩最小的排放角度作為該零件的最優入排方案。

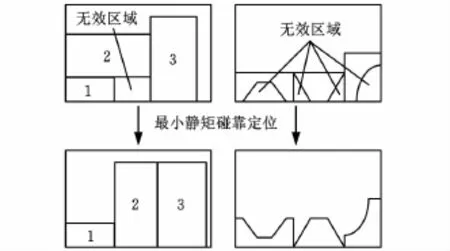
圖1 入排零件的最小靜矩碰靠定位的排樣布局優化

形心及靜矩的求解采用正負梯形分割法，即將多邊形通過各頂點分割成多個梯形的組合，規定多邊形逆時針方向面積為正，順時針方向面積為負，其中需要注意多邊形各邊的次序和方向。如圖2所示，以五邊形為例，多邊形面積可表示為

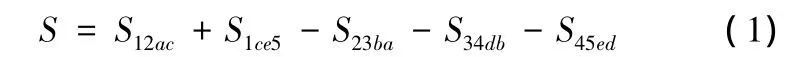
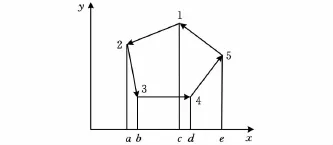
圖2 多邊形面積計算

在實際下料中，板材一般為均質體(即密度相同)且厚度統一，因此排樣零件的形心計算可簡化為求解平面多邊形的形心，如圖3所示，多邊形形心求解公式為

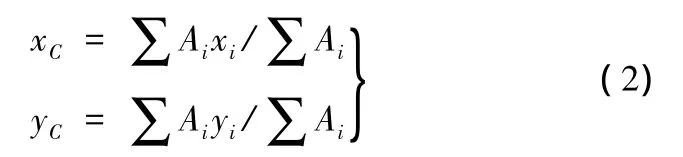
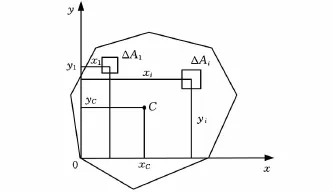
圖3 零件多邊形的形心坐標

對水平方向的靜矩為

式中，Ai為零件圖形劃分的單元面積;∑Ai為零件多邊形的面積;(xi，yi)分別為各單元的形心坐標;Sx為圖形對于x軸的靜矩或稱對于x軸面積的一次矩。

多邊形繞其形心進行旋轉變換以矩陣表示為

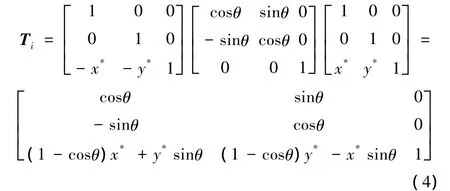
從而得到旋轉后的位置坐標為

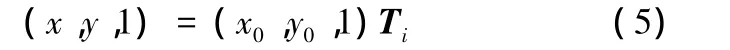
式中，(x0，y0)為初始坐標;(x，y)為旋轉后的坐標;θ為旋轉角度。

通常可根據實際情況設置旋轉角度間隔Δθ，每個零件以不同入排角度定位后對其靜矩值進行比較，取靜矩最小實現入排角度的優化。

零件多邊形的數據結構定義如下:

1.2 碰靠距離計算

零件碰靠處理的關鍵步驟是計算兩個零件的碰靠距離即零件按照指定的方向與另一個零件發生碰撞時的移動量。一般定義下的零件幾何外形輪廓是由若干基本實體或圖元(如直線、圓弧、曲線等)組成，碰靠距離可通過計算基本實體間的最短距離來獲得。文獻［7］論述了各種基本圖元間(如線與線、線段與圓弧、圓弧與圓弧)碰靠距離的計算方法，從而實現零件的平移和靠接操作。研究表明，不規則零件中各實體(尤其是弧等曲線)的碰靠計算復雜度較高，影響排樣系統的執行效率。本文采用了一種簡單而有效的方法來計算碰靠距離，即對零件圖形中各圖元外輪廓進行離散化處理，用若干個離散點形成的連續的直線段構建多邊形來近似描述零件圖形，這樣將碰靠運算轉化為各離散點與離散點構成的直線段沿碰靠方向的求交和求距的計算，最終取其最小值作為碰靠距離。圖元離散化過程簡化了圖形的表示方法，如直線段只需提取其起始點和終止點;圓弧則因規則性以其起始點和終止點(包含之)來均分得到各離散點;對于復雜曲線則根據其曲率變化適當選擇離散點。

假設給定兩個零件圖形P和Q，碰靠方向為水平方向(其中任意方向都可以通過圖形變換將其轉化為所需碰靠方向，這樣便于描述計算)，其碰靠距離求解算法的主要步驟如下。

(1)離散化圖形P和Q，分別產生各自的離散頂點序列:P={p1，p2，…，pn}和 Q={q1，q2，…，qm}。其中各頂點的坐標可表示為(X(pi)，Y(pi))或(X(qj)，Y(qj))。

(2)計算圖形P上各頂點到Q的距離。對于點 pi(i=1，2，…，n)，遍歷 Q 上所有頂點 qj(j=1，2，…，m)，如果滿足條件:Y(qj+1)≤ Y(pi)≤Y(qj)或Y(qj)≤Y(pi)≤Y(qj+1)，則計算pi點沿水平方向的直線與線段qjqj+1的交點并求出pi與交點的距離記為dij;否則計算下一個點pi+1直到完成P上所有頂點的計算。從所得距離中取最小距離值min dij。

(3)同樣方法計算圖形Q上各頂點到P的距離，得到最小距離min d'ij。

(4)比較min dij和min d'ij，取其最小者為零件P和Q的碰靠距離，將零件Q或P以此值作為移動量進行平移操作，實現兩個零件的靠接，如圖4所示。

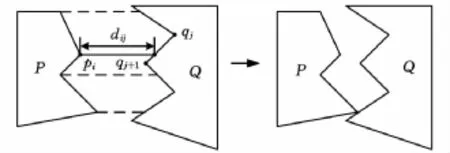
圖4 零件的碰靠計算

2 基于最佳吻合碰靠的排樣算法

在零件以一定的次序排入過程中，首先在給定的排放區域內通過計算當前零件不同排放角度的靜矩，選擇最小靜矩的入排角度。然后根據設定的碰靠方向，對當前零件進行碰靠操作，為減小計算量，通常以水平和垂直方向作為碰靠方向，使零件盡可能緊密靠接，并以當前排樣高度最低作為最佳碰靠定位方案。因此，最佳吻合碰靠過程從某種意義上說是使零件在最小靜矩的排放規則基礎上再進行碰靠處理從而搜索到排放高度最低的位置。圖5給出了零件通過旋轉碰靠實現較好的定位排樣效果。

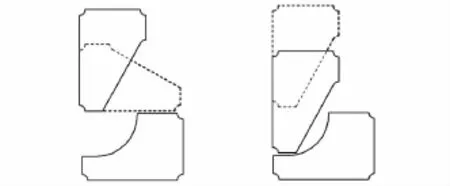
圖5 最佳吻合碰靠定位示意

此外對于形狀較復雜零件，本文設計的排樣系統增加了交互式點對點碰靠方法作為輔助碰靠定位，即依靠人類的先驗知識和感官判斷，對入排零件可以人為調整選擇最佳的碰靠方向使零件沿著規定的靠接定位位置移動，如圖6所示。

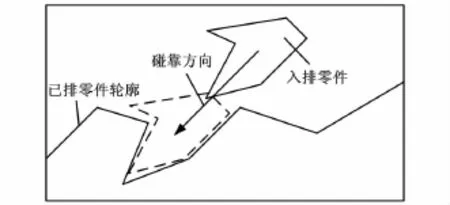
圖6 交互點對點碰靠

無論是自動碰靠還是交互碰靠，評價最佳吻合碰靠定位的目標函數是零件向下向左移動的最大距離或零件實現靠接后的最低排樣高度，對于相同排樣高度的情況，優先最左靠接位置。目標函數表示為

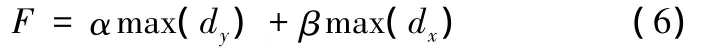
其中，max(dy)表示高度方向最大碰靠距離，max(dx)表示水平方向最大碰靠距離;α和β為參數因子，α?β，以保證當前面的函數值不同時，后面的函數值不會對結果的判斷造成影響。

碰靠排樣算法流程如圖7所示，圖中虛框中所表示的外循環表示對于排樣零件入排次序的優化，優化方法可采用遺傳算法、粒子群算法等，可參閱文獻［8-9］，本文著重討論定序情況下的定位碰靠方法，故對其不作詳細闡述。

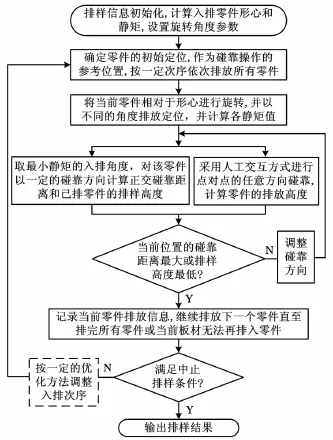
圖7 最佳吻合碰靠流程圖

3 應用實例

通過對上述算法的描述和分析，本文設計排樣系統平臺，以剩余矩形法作為解碼算法結合自動碰靠算法實現零件定位和排樣布局。選擇板材長度為8000mm，寬為2000mm。輸入兩組待排零件，其中以已排零件的面積之和與板長方向的零件包絡矩的最高輪廓線以下區域面積S的比率作為材料利用率的評價函數，其目標評價函數表示為

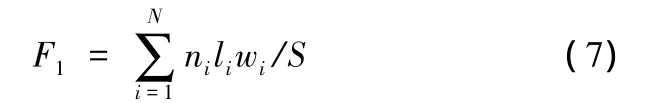
式中，ni為排樣零件個體;li為零件包絡矩長度;wi為零件包絡矩寬度;N為入排零件個數;S為整體排樣結構的包絡面積。

圖8為69個零件的排樣圖，板材利用率為86.87%;圖9為43個零件的排樣圖，板材利用率為85.63%。

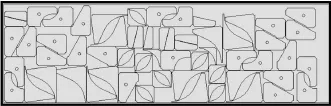
圖8 排樣布局一

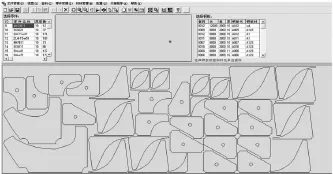
圖9 排樣布局二

4 結束語

本文在借鑒矩形化策略基礎上，將零件以最小靜矩(或最低重心)為定位準則選擇最佳入排角度進行正交靠接排放和定位，并設計了交互排樣中的點對點交互碰靠算法，實現零件以任意碰靠方向進行最優布局調整。碰靠距離的計算采用零件圖形離散化處理，實現離散點沿碰靠方向的求交和求距，求解方便簡單。利用該算法設計的排樣系統在對不規則零件的排樣優化中具有較好的穩定性和有效性。

［1］Jakobs S.On Genetic Algorithms for the Packing of Polygons［J］.Eurpean Journal of Operational Research，1996，88:165-181.

［2］Bennell J A，Kathryn A，Dowsland W B.The Irregular Cutting－stock Problem－A New Procedure for Deriving the No－fit Polygon［J］.Computers and Operations Research，2001，28:271-287.

［3］劉嘉敏，佟德剛，黃有群.臨界多邊形生成算法的改進［J］.沈陽工業大學學報，2005，27(5):567-570.Liu Jiamin，Tong Degang，Huang Youqun.An Improved Approach for No－fit Polygon Creation［J］.Journal of Shenyang University of Technology，2005，27(5):567-570.

［4］Hopper E，Turton B C H.A Genetic Algorithm for 2D Industrial Packing Problem［J］.Computers and Industrial Engineering，1996，37:375-378.

［5］Ismail H S，Hon K K B.The Nesting of Two－dimensional Shapes Using Genetic Algorithms［J］.Proceeding of the Institution of Mechanical Engineers，1995，209(2):115-124.

［6］劉胡瑤，何援軍.基于重心NFP的二維不規則形狀排樣算法［J］.中國機械工程，2007，18(6):723-726.Liu Huyao，He Yuanjun.2D Irregular Nesting Algorithm Based on Gravity Center NFP［J］.China Mechanical Engineering，2007，18(6):723-726.

［7］陳文亮，崔英，李磊.基于自動碰撞技術的最優排樣算法［J］.計算機應用研究，2000，17(7):37-39.Chen Wenliang，Cui Ying，Li Lei.The Optimized Nest Algorithm Based on Automatic Touching Technology［J］.Application Research of Computers，2000，17(7):37-39.

［8］梁利東，葉家瑋.基于遺傳算法的不規則件優化排樣的研究［J］.計算機工程與應用，2009，45(2):223-224，228.Liang Lidong，Ye Jiawei.Research of Irregular Parts with Genetic Algorithm［J］.Computer Engineering and Application，2009，45(2):223-224，228.

［9］梁利東，鐘相強.基于粒子群優化算法在不規則件排樣中的應用［J］.中國機械工程，2010，21(17):2050-2052，2069.Liang Lidong，Zhong Xiangqiang.Application of Particle Swarm Optimization for Solving Irregular Parts Nesting Problem［J］.China Mechanical Engineering，2010，21(17):2050-2052，2069.