基于PSO差分-共射負反饋放大電路參數的自適應優化

楊一軍,陳得寶,王江濤,丁國華

(淮北師范大學 物理與電子信息學院,安徽 淮北 235000)

Kennedy等[1]提出的粒子群優化算法(PSO)由于具有易編程和收斂快等優點而引起人們廣泛關注,并使其理論得到迅速發展. 如Ratnaweera等[2]將變異理論引入PSO算法中,采用變加速系數算法,有效控制了本地搜索和收斂,達到全局最優解;Sari等[3]將PSO算法應用于燃料電池電路設計中;Pedersen等[4]通過調整自身行為參數,提出一種簡化粒子群算法;Mousa等[5]結合遺傳算法和粒子群優化算法,提出了混合粒子群優化算法的多目標優化方法;郭新辰等[6]利用PSO算法求解殘差平方和的極小化優化問題,得到逼近解.

當放大緩慢變化的小信號時,多采用直接耦合多級放大方式,由于存在零點漂移和配置級間電平,并需考慮交流指標參數等,因此工程上常先做近似處理,以簡化設計,再通過調試,逐步逼近. 本文以直接耦合方式下的差分-共射電壓并聯負反饋放大電路為例,以高互阻增益、 大共模抑制比和低輸出電阻為設計要求,采用PSO算法,編寫程序優化電路參數,并利用虛擬電子工作臺(EWB)仿真驗證.

1 電路設計

1.1 直流電位分析

差分-共射電壓并聯負反饋放大電路如圖1所示. 其中: 第一級放大電路為差分結構,有較強的抑制零點漂移能力;第二級為共發射極放大電路,有較好的電壓和電流放大能力;電鍵位于A為反饋放大器,位于B為基本放大器. 在基本放大器的直流電位計算中,反饋電阻Rf遠大于RS,與RS并聯后可忽略不計. 由于晶體差分對管T1和T2基極電流為小電流,RS,RB1和RB2的電阻值均較小,因此可略去其上的直流壓降,認為T1和T2的直流輸入對稱,靜態電流IE1和IE2相等,有

(1)

圖1 差分-共射電壓并聯負反饋放大電路Fig.1 Circuit diagram of differential-common emitter amplifying circuit

根據圖1電路可建立方程組:

VC2-VCC/RC2+IB3+IC2=0,

(2)

VC2-RB3IB3-VBE-RE3(1+β3)IB3=0.

(3)

不失一般性,在電路中設各晶體管的β值均相同. 根據放大狀態下IC和IE的關系,可求得VC2和IB3.

1.2 交流指標

1.2.1 基本放大器電壓增益 利用增益相互轉換關系,可先求多級放大器的電壓增益Av,再求互阻增益Ar. 在同相輸出條件下,由差分電路組成的第一級電壓增益為

(4)

其中:Ri2=RB3+rbe3+(1+β)RE3為第二級放大電路的輸入電阻;rbe1和rbe3可由式

rbe=rbb′+(1+β)VT/IE

(5)

計算. 由共發射極構成第二級的電壓增益為

Av2=(-βRC3∥Rf∥RL)/Ri2,

(6)

放大器總電壓增益Av為

Av=Av1·Av2.

(7)

利用不同增益間的相互轉換,可將電壓增益轉為互阻增益

(8)

其中Ri=2(RB1+rbe1)∥Rf為考慮反饋網絡負載效應后的差分-共射負反饋放大器的輸入電阻. 其源互阻增益為

∥Ri)Av.

(9)

1.2.2 共模抑制比 當單端輸入、 單端輸出時,差分放大器的差模電壓增益Avd=Av1,共模電壓增益Avc為

(10)

由定義可得共模抑制比

(11)

由于第二級為采用直接耦合方式的共發射極放大電路,它對差模和共模的放大能力相同,因此差放的共模抑制比即為整個放大器的共模抑制比.

1.2.3 反饋放大器互阻增益 由電路可得反饋系數

kfg=-1/Rf,

(12)

再利用反饋放大器與基本放大器的關系

Arf=Ar/(1+kfgAr)

(13)

可得反饋放大器的互阻增益.

1.2.4 輸出電阻 根據反饋放大器輸出電阻Rof與Ro間的關系

Rof=Ro/(1+kfgArst)

(14)

及圖1可得基本放大器輸出電阻Ro=RC3∥Rf,其中Arst為負載開路時的源互阻增益.

2 基于粒子群算法的電路參數優化

2.1 優化電路參數

2.1.1RB1和RB2的設置 由式(4)和(11)可知,晶體差分對管的基極電阻RB1和RB2越小,越有利于提高開環增益和共模抑制比,因此在算法中限定最小變量值為10 Ω,以驗證其優化效果.

2.1.2 發射極電阻RE3的設置 由式(4)可知,RE3增大可提高Av1;由式(6)可知,RE3增大將減小Av2. 受RC2制約,當RE3增大時,Av1增加較小,Av2減小較大. 由于RE3取較大值時有利于設置T3管的靜態工作點,因此在算法中設置若其小于500 Ω,則令其等于500 Ω.

2.1.3 放大區的工作條件 在優化電路參數時,需考慮電流的實際流向,算法中使用限制條件IC2>0和IC3>0;根據晶體管工作在放大區和動態范圍的需要,令1 V1.2 V. 同時取VCC=12 V,VEE=-12 V,RS=1.5 kΩ,RL=50 kΩ,β=100,rbb′=100 Ω.

2.1.4 適應度函數的選擇 差分-共射電壓并聯負反饋放大器對共模信號具有較強的抑制能力,其交流參數的互阻增益較大,輸入和輸出電阻較小. 因此選擇高共模抑制比、 大互阻增益和小輸出電阻作為適應度函數.

2.2 標準粒子群優化算法簡介

粒子群算法模擬動物捕食原理,利用動物跟蹤當前群體和記憶自身經歷過的最好位置,實現對問題的優化. 即先隨機產生初始解,再通過進化迭代找到最優解. 在每次迭代中,粒子通過跟蹤自身和整個種群中當前找到的最優解進行更新.

粒子位置更新方程[1]為

Xi(k+1) =Xi(k)+Vi(k+1),

(15)

其中:Xi(k+1)和Xi(k)分別為k+1時刻和k時刻第i個粒子的位置;Vi(k+1)為k+1時刻該粒子的運動速度. 速度更新方程為

Vi(k+1)=wVi(k)+c1rand(·)(Xpbesti(k)-Xi(k))+c2rand(·)(Xgbest(k)-Xi(k)),

(16)

其中:c1和c2為學習因子(常數);Xpbesti和Xgbest分別為系統進化迭代至當前代時,第i個粒子的最好位置和整個粒子群中最優粒子位置;rand(·)為0～1間的隨機數;w為加權因子,隨更新次數的增加而線性減小,可表示為

(17)

其中:wmax為最大加權因子;wmin為最小加權因子;gen為當前更新代數;maxgen為最大更新代數.

為限制粒子在一定范圍內運動,所有粒子運動應遵循如下限制條件:

1) 若X>Xmax,則X=Xmax;若XVmax,則V=Vmax;若V<-Vmax,則V=-Vmax. 其中Vmax,Xmax和Xmin分別為粒子允許運動的最大速度、 最大和最小位置. 利用限制條件1)可避免在全局最優解附近出現“振蕩”現象.

2.3 反饋放大器參數的優化

2.3.1 算法參數設置 粒子群運動范圍Vmax=10,Xmax=1 000 000,Xmin=10;最大進化迭代數maxgen=30 000;常數c1=c2=2;wmax=0.9;wmin=0.4. 根據互阻增益、 共模抑制比和輸出電阻的計算要求,按表1所列的粒子編碼表,隨機初始化一組群體.

表1 粒子編碼Table 1 Particle code

2.3.2 計算各粒子的適應度值 根據設計高互阻增益、 高共模抑制比和低輸出電阻的要求,定義f=ArfKCMR/Rof作為粒子的適應度函數.

2.3.3 最好位置的選擇和更新 計算和保存各粒子和所有粒子運動到當前進化代數的最好位置. 按式(15)～(17)及限制條件1),2)對粒子位置進行更新至算法結束. 否則重新計算各粒子的適應度值.

在優化過程中,對互阻增益Arf(分別大于200,225,250,275,300 kΩ)和輸出電阻Rof(分別大于200,250,300,350,400 Ω)進行限制,以考察適應度函數的變化. 優化后的各電阻值(電路參數值)列于表2.

表2 電路電阻參數Table 2 Resistance parameters for the circuit

2.4 結果與討論

1)RB1=10 Ω,Xmin=10為粒子允許運動的最小位置;RE3=500 Ω為算法中限制的最小值,在優化過程中,它們的值越小,越有利于增大適應度函數f.

2) 當僅設定Rof>200 Ω或Arf>200 kΩ時,對電路優化沒有影響(表2中第2行),此時f取最大值.

3) 由式(14)可知,RC3對Rof影響較大,當需要Rof較小時,RC3越小越好;由式(4),(6)～(8)和(13)可知,當需要高互阻增益時,RC2和RC3越大越好. 算法在參數優化過程中以增大RC2、 提高Arf、 減小RC3及降低Rof的方式,獲得最大f. 當Arf受限時,增大RC3以提升Arf;當Rof受限時,RC3和Arf增大,f減小.

圖2 RC3,f,Rof和Arf的關系曲線Fig.2 Relation curves between RC3,f or Rof and Arf

4) 圖2為RC3,f,Rof和Arf的關系曲線. 由圖2可見,隨著Arf增大,RC3和Rof增加,f單調減小,這是由于對f中某些參數限制形成條件優化后,Arf均從右邊趨近于設定的最小值,以使f在受限制條件下獲得最大所致.

5) 由表2中7～10行可見,Rof限定的最小值與第2行不加條件限制的220.69 Ω偏離越大,f越小,原因同上.

6) 對共模抑制比進行限制,也有類似現象.

7) 根據工程實際,可對某個參數進行限制或加權處理(如乘方和取對數等),優化后以滿足特定需求.

3 EWB仿真

將圖1中電阻用表2中2～6行數據替代,啟動EWB仿真軟件,并觀察閉環下輸入電流、 輸出電壓和互阻增益Arf. 由相對誤差=|理論值-仿真值|/理論值×100%可得PSO算法與仿真結果間的相對誤差,結果列于表3. 由表3可見:Arf的PSO算法與EWB仿真結果相對最大誤差小于0.515%,在工程上吻合較好,表明電路參數合適,晶體管工作于放大區;隨著Arf增大,仿真與理論結果的相對誤差減小,最后轉為負誤差,這與rbb′選取有關. 在一定范圍內,若rbb′較大,則rbe增大,Ar和Arf的理論值減小,即不產生負誤差.

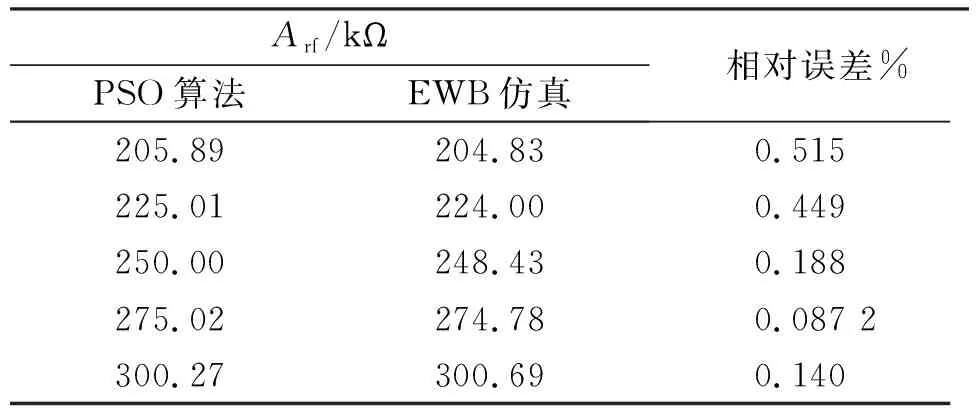
表3 EWB仿真和PSO算法的相對誤差Table 3 Relative errors between simulating with EWB and PSO algorithm

綜上,本文以閉環互阻增益和共模抑制比乘積對輸出電阻的比為適應度函數,結合差分-共發射極電路的設計要求,采用粒子群優化算法得到了電路的電阻值,從而得到了優化電路. 反饋放大器互阻增益與EWB仿真結果相符. 當對放大器某交流指標進行設計時,適應度函數值均減小,并趨于該指標的底限以獲取適應度函數的最大值. 表明在設計多級反饋放大電路時,既可根據對放大器不同性能指標的要求,選擇不同的指標參數優化,也可修改某些指標的數值(或采用對指標加權,定義適應度函數)實現參數優化,以取得實際需要的最佳效果.

[1] Kennedy J,Eberhart R C. A New Optimizer Using Particle Swarm Theory [C]//Proc of the 6th International Symposium on Micro Machine and Human Science. Nagoya: [s.n.],1995: 39-43.

[2] Ratnaweera A,Halgamuge S K,Watson H C. Self-organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients [J]. IEEE Transactions on Evolutionary Computation,2004,8(8): 240-255.

[3] Sari A,Espanet C,Hissel D. Particle Swarm Optimization Applied to the Co-design of a Fuel Cell Air Circuit [J]. Journal of Power Sources,2008,179(1): 121-131.

[4] Pedersen M E H,Chipperfield A J. Simplifying Particle Swarm Optimization [J]. Applied Soft Computing,2010,10(2): 618-628.

[5] Mousa A A,El-Shorbagy M A,Abd-El-Wahed W F. Local Search Based Hybrid Particle Swarm Optimization Algorithm for Multiobjective Optimization [J]. Swarm and Evolutionary Computation,2012,3: 1-14.

[6] GUO Xin-chen,WU Xi,CHEN Shu-kun,et al. Hybird Method Based on RBFNN and PSO for Solving Linear Volterra Integral Equations of the Second Kind [J]. Journal of Jilin University: Science Edition,2010,48(4): 658-661. (郭新辰,吳希,陳書坤,等. 基于RBFNN和PSO求解第二類Volterra積分方程的混合方法 [J]. 吉林大學學報: 理學版,2010,48(4): 658-661.)