求解加權(quán)Euclidean單中心問題的SMO-型算法

叢 偉 杰

(西安郵電大學(xué) 理學(xué)院,西安 710121)

0 引 言

給定點(diǎn)集P={p1,p2,…,pm}?Rn和對(duì)應(yīng)的正權(quán)重W=(w1,w2,…,wm}；加權(quán)Euclidean單中心(weighted Euclidean one-center,簡(jiǎn)記為WEOC)問題就是尋找一個(gè)點(diǎn)c∈Rn,最小化P中各點(diǎn)到c加權(quán)Euclidean距離的最大值. 給定(P,W)的WEOC問題記為WEOC(P,W),可表示為

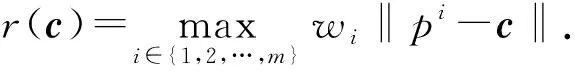
WEOC問題[1-3]是計(jì)算幾何中的經(jīng)典問題,在現(xiàn)代工程學(xué)和數(shù)學(xué)領(lǐng)域應(yīng)用廣泛,尤其在設(shè)施選址問題上[4-5]. 當(dāng)WEOC問題中的所有權(quán)重wi=1時(shí),WEOC問題即退化為最小閉包球(minimum enclosing ball,簡(jiǎn)記為MEB)問題[6],即尋找一個(gè)半徑最小的球包含點(diǎn)集P中的所有點(diǎn).

序列最小最優(yōu)化(sequential minimal optimization,簡(jiǎn)記為SMO)方法[7]是支持向量機(jī)中求解凸二次優(yōu)化問題的主要工具,與一般傳統(tǒng)優(yōu)化迭代方法不同,SMO方法在每次迭代過程中只需更新決策變量的兩個(gè)分量,節(jié)省了計(jì)算時(shí)間,能加速算法的執(zhí)行. 本文首先定義了求解WEOC問題的兩個(gè)近似最優(yōu)性條件,然后基于SMO方法的思想,提出一種求解WEOC問題的SMO-型算法. 該算法求解WEOC問題滿足第二個(gè)近似最優(yōu)性條件的(1+ε)-近似解. 數(shù)值實(shí)驗(yàn)結(jié)果驗(yàn)證了算法的有效性.

1 優(yōu)化公式及近似最優(yōu)性條件

WEOC(P,W)問題可以轉(zhuǎn)化為如下優(yōu)化問題:

(1)

其中c=(c1,c2,…,cn)T∈Rn和r∈R是原始變量. 文獻(xiàn)[3]通過平方問題(1)的約束并定義γ=r2,將問題(1)轉(zhuǎn)化為如下凸優(yōu)化問題:

(2)

(3)

其中u=(u1,u2,…,um)T∈Rm是對(duì)偶變量. 由問題的KKT最優(yōu)性條件[3]可得

(4)

其中(c*,r*)∈Rn×R和u*∈Rm分別為原規(guī)劃(1)和對(duì)偶規(guī)劃(3)的最優(yōu)解. 因此,WEOC(P,W)問題能轉(zhuǎn)化為求解對(duì)偶規(guī)劃(3).

(5)

下面類似于MVAE問題的近似最優(yōu)性條件[8],給出WEOC問題的兩個(gè)近似最優(yōu)性條件定義.

定義1給定ε>0,如果

wi‖pi-c‖≤(1+ε)r,i=1,2,…,m,

(6)

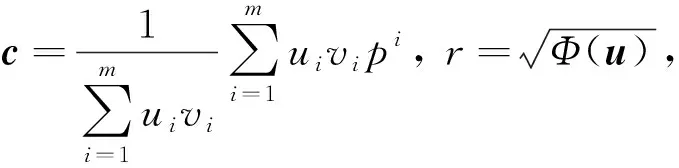
定義2給定ε∈(0,1),如果式(6)成立,并且有

ui>0 ?wi‖pi-c‖≥(1-ε)r,i=1,2,…,m,

(7)

則稱對(duì)偶規(guī)劃(3)的可行解u滿足強(qiáng)ε-近似最優(yōu)性條件.

由定義2可知,當(dāng)ui>0時(shí),有(1-ε)r≤wi‖pi-c‖≤(1+ε)r(i=1,2,…,m),表明對(duì)于充分小的ε,定義2是比定義1對(duì)式(5)更好的近似.

2 SMO-型算法

下面給出求解WEOC(P,W)問題的SMO-型算法.

算法1給定P={p1,p2,…,pm}?Rn,W={w1,w2,…,wm},ε>0.

4) 令

算法1中1)是簡(jiǎn)單的初始化過程,與文獻(xiàn)[3]中算法5.1的初始化過程相同. 算法1與算法5.1[3]的主要不同在于主循環(huán)部分,在第k次迭代中,由2)和3)可得

wi+‖pi+-ck‖=(1+ε+)rk≤(1+εk)rk,wi-‖pi--ck‖=(1-ε-)rk≥(1-εk)rk,

表明每次迭代算法1總能得到對(duì)偶規(guī)劃(3)的一個(gè)可行解uk滿足強(qiáng)εk-近似最優(yōu)性條件. 因此,當(dāng)算法終止(εk≤ε)時(shí),得到的可行解uk滿足強(qiáng)ε-近似最優(yōu)性條件(6),(7),并且有

由WEOC(P,W)的(1+ε)-近似解定義知,算法1終止時(shí),得到問題的一個(gè)(1+ε)-近似解為(ck,r(ck))∶=(ck,(1+εk)rk).

算法5.1[3]給出的可行解迭代更新公式為uk+1=(1-λk)uk+λkei+=uk+λk(ei+-uk)或uk+1=(1+λk)uk-λkei-=uk+λk(uk-ei-),其中ei表示第i個(gè)分量為1的單位向量. 它們使用了兩個(gè)不同的搜索方向dk∶=ei+-uk或uk-ei-,導(dǎo)致算法5.1[3]計(jì)算非常復(fù)雜的步長(zhǎng)λk. 基于SMO方法的思想,每次迭代僅更新可行解的兩個(gè)分量,算法1中4)給出的可行解迭代更新公式為

uk+1=uk+λk(ei+-ei-),

(8)

其中搜索方向?yàn)閐k∶=ei+-ei-,使得算法1能夠計(jì)算一個(gè)相對(duì)簡(jiǎn)單的步長(zhǎng)λk.

(9)

ck+1=(1-(σ+-σ-))ck+σ+pi+-σ-pi-.

(10)

對(duì)于任意的x,y,z∈Rm和σ1,σ2∈R ,易驗(yàn)證下式成立:

下面計(jì)算算法1中的步長(zhǎng)λk. 由前面的計(jì)算可得Φ(uk+1)=Φ(uk)+Δk(λk),其中

(12)

對(duì)式(12)中關(guān)于λ的函數(shù)Δk(λ)分別求一、 二階導(dǎo)數(shù),得

3 數(shù)值實(shí)驗(yàn)

為了驗(yàn)證本文提出SMO-型算法的有效性,對(duì)于相同的數(shù)據(jù)集,在Matlab中同時(shí)執(zhí)行文獻(xiàn)[3]中的算法5.1和本文的算法1. 實(shí)驗(yàn)中用到的數(shù)據(jù)集是由函數(shù)randn(n,m)隨機(jī)產(chǎn)生的正態(tài)分布數(shù)據(jù),對(duì)應(yīng)的權(quán)重是由函數(shù)rand(1,m)隨機(jī)產(chǎn)生的均勻分布數(shù)據(jù),其中(n,m)=(10,10 000)～(100,100 000). 對(duì)于每對(duì)固定的(n,m),隨機(jī)產(chǎn)生10組不同的數(shù)據(jù)執(zhí)行算法,得到的結(jié)果以其算術(shù)平均值形式給出.

表1列出了當(dāng)精度ε=10-7時(shí),兩個(gè)算法執(zhí)行的迭代次數(shù)和CPU時(shí)間的比較結(jié)果. 由表1可見: 算法1總比算法5.1[3]運(yùn)行速度快,一般在迭代次數(shù)和CPU時(shí)間上比算法5.1減少41%～56%;對(duì)于n=100,m=100 000的大規(guī)模數(shù)據(jù),算法1僅需要執(zhí)行約90 s,表明算法1能有效求解高精度的大規(guī)模計(jì)算問題.

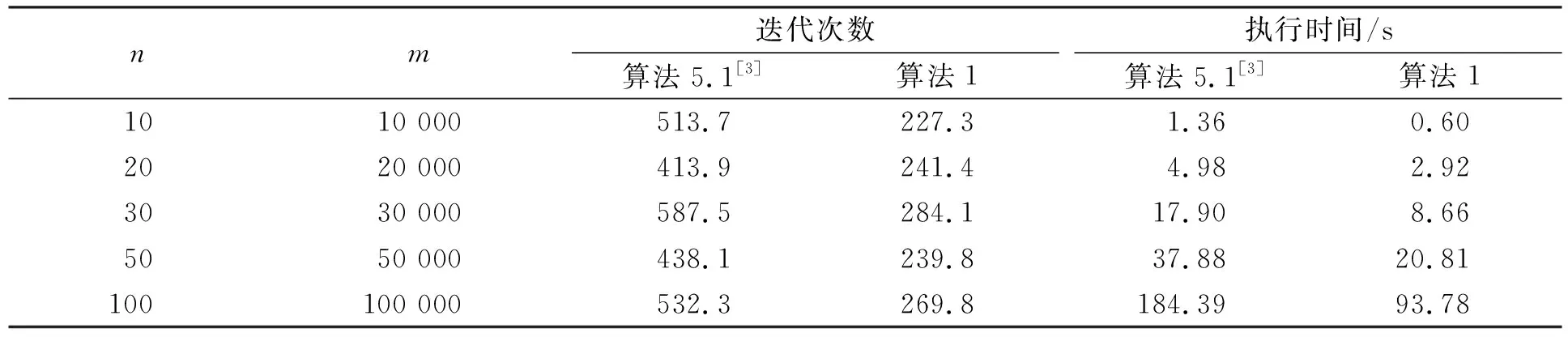
表1 算法5.1[3]和算法1在高精度ε=10-7下的數(shù)值結(jié)果比較Table 1 Comparisons of numerical results by virtue of algorithms 5.1[3] and 1 with ε=10-7

[1] Megiddo N. The Weighted Euclidean 1-Center Problem [J]. Mathematics of Operations Research,1983,8(4): 498-504.

[2] Megiddo N,Zemel E. AnO(nlogn) Randomizing Algorithm for the Weighted Euclidean 1-Center Problem [J]. Journal of Algorithms,1986,7(3): 358-368.

[3] Kumar P,Yildirim E A. An Algorithm and a Core Set Result for the Weighted Euclidean One-Center Problem [J]. Informs Journal on Computing,2009,21(4): 614-629.

[4] Drezner Z,Gavish B.ε-Approximations for Multidimensional Weighted Location Problems [J]. Operations Research,1985,33(4): 772-783.

[5] Drezner Z. The Weighted Minimax Location Problem with Set-up Costs and Extensions [J]. Operations Research,1991,25(1): 55-64.

[6] CONG Wei-jie,LIU Hong-wei. An SMO-Type Method for Solving the MEB Problem [J]. Journal of Northwest University: Natural Science Edition,2010,40(6): 965-969. (叢偉杰,劉紅衛(wèi). 求解MEB問題的一種SMO-型方法 [J]. 西北大學(xué)學(xué)報(bào): 自然科學(xué)版,2010,40(6): 965-969.)

[7] Chen P H,Fan R E,Lin C J. A Study on SMO-Type Decomposition Methods for Support Vector Machines [J]. IEEE Transactions on Neural Networks,2006,17(4): 893-908.

[8] CONG Wei-jie,LIU Hong-wei. Linearly Convergent Algorithm for Solving the Minimum Volume Axis-Aligned Ellipsoid Problem [J]. Journal of Jilin University: Science Edition,2011,49(2): 173-178. (叢偉杰,劉紅衛(wèi). 求解最小體積軸向橢球問題的線性收斂算法 [J]. 吉林大學(xué)學(xué)報(bào): 理學(xué)版,2011,49(2): 173-178.)