花崗巖殘積土鄧肯-張模型參數的合理確定

賴榕洲，吳能森，徐 青

(福建農林大學 交通與土木工程學院，福建 福州 350002)

花崗巖殘積土鄧肯-張模型參數的合理確定

賴榕洲，吳能森，徐 青

(福建農林大學 交通與土木工程學院，福建 福州 350002)

為合理確定花崗巖殘積土的鄧肯-張模型參數，制作3種不同含水率的試樣，分別在圍壓100 kPa、200 kPa和300 kPa條件下進行固結排水三軸試驗，得到的應力～應變關系曲線均呈非線性加工硬化型，符合鄧肯-張模型的適用條件。然后分別采用“全點法”和“兩點法”求取鄧肯-張模型參數，并利用求取結果對模型曲線進行擬合，結果表明：“全點法”因不可避免要受到異常數據的干擾，所求取模型參數精度較低，而“兩點法”僅使用高應力水平的兩組數據，不僅簡單、方便，且可以避免低應力階段異常數據的干擾，所求取模型參數精度較高。建議工程上采用“兩點法”確定花崗巖殘積土的鄧肯-張模型參數。

花崗巖殘積土；鄧肯-張模型；三軸試驗；全點法；兩點法

花崗巖殘積土是花崗巖經過物理風化和化學風化后殘留在原地的碎屑物，具有特殊的成分和結構特征，屬區域性特殊土，在我國南方分布廣泛。[1]鄧肯-張模型能較好地反映土體的非線性，且概念清晰，模型參數明確易得，便于工程應用。[2]在巖土及地下工程分析計算中，需要具體的鄧肯-張模型參數值，在土體本構模型適用的前提下，其模型參數的精確性決定了分析計算結果的可靠性。[3]為此，擬對花崗巖殘積土進行常規三軸試驗，應用兩種不同方法求取鄧肯-張模型的參數值，并通過擬合曲線和試驗曲線的對比，分析兩種方法的精確性，據此提出合理確定花崗巖殘積土鄧肯-張模型參數的建議。

1 鄧肯-張模型簡介

1963年，康納(Kondner)[4]在大量三軸試驗基礎上，提出圍壓為常數的常規三軸固結試驗的加工硬化型應力～應變關系可近似地用雙曲線來表示，即：

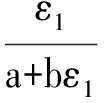
(1)

式中，a、b為試驗常數，ε1為軸向應變，σ3為圍壓，σ1為軸向主應力。

可將式(1)改寫為：

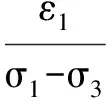
(2)

式(2)是一直線方程，a、b分別為該直線的截距、斜率，可通過試驗數據擬合直線獲得。

1970年，鄧肯(Duncan)和張(Chang)等[5]根據式(1)提出了包括切線模量Et和切線泊松比μt的鄧肯-張本構方程式，簡稱鄧肯-張模型E-μ模型，其中切線模量Et表達式為：

(3)

(4)

式中：Ei為初始切線模量(kPa)，c為土的粘聚力(kPa)，φ為土的內摩擦角(°)，Rf為破壞應力比，K、n為試驗常數，Pa為大氣壓力(取101.4 kPa)。

Ei、Rf與a、b的關系為：

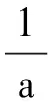
(5)

Rf=b(σ1-σ3)f

(6)

式中，(σ1-σ3)f為土樣破壞時的偏應力。

將式(4)進行坐標變換，可變為lgEi～lgσ3直線，則該直線斜率為n，當lgσ3=1時的lgEi值即為lgK。

在鄧肯-張模型的計算中，常用應力水平S來衡量土體強度發揮的程度：

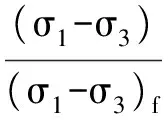
(7)

式中各變量意義同上。

2 試驗概況

試驗土樣取自福州晉安區鶴林新城二區某地塊，取土深度12.3～16.8 m，土樣呈褐黃、肉紅色，硬塑狀態，原狀土含水率ω=30.1%，密度ρ=1.84 g/cm3，土粒相對密度ds=2.72。試驗儀器為SLB-1型應力～應變控制式三軸剪切滲透試驗儀，采用固結排水三軸壓縮試驗(CD試驗)[6]。土樣經風干、碾碎、過孔徑為2 mm篩后，分別取含水率13%、17%、21%，按擊實法制備試樣，試樣直徑39.1 mm，高80 mm。試驗固結圍壓σ3分別取100 kPa、200 kPa、300 kPa，當體積讀數變化微小或長時間保持不變時認為試樣完成固結。固結完成后，在圍壓σ3保持不變的情況下，采用應變控制方式，以0.012%/min剪切速率增加軸向壓力進行排水剪切，直至試樣軸向應變值達到15%時停止試驗，試驗過程中排水閥始終保持開啟狀態。

試驗數據及相關曲線由儀器自動采集和繪制，如試樣的主應力差(σ1-σ3)與軸向應變ε1關系曲線(圖1)。

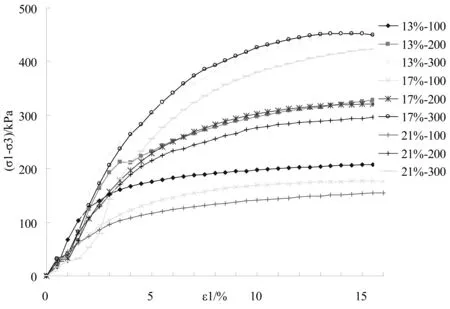
圖1 (σ1﹣σ3)～ε1關系曲線 Fig.1 The curves of (σ1﹣σ3)～ε1

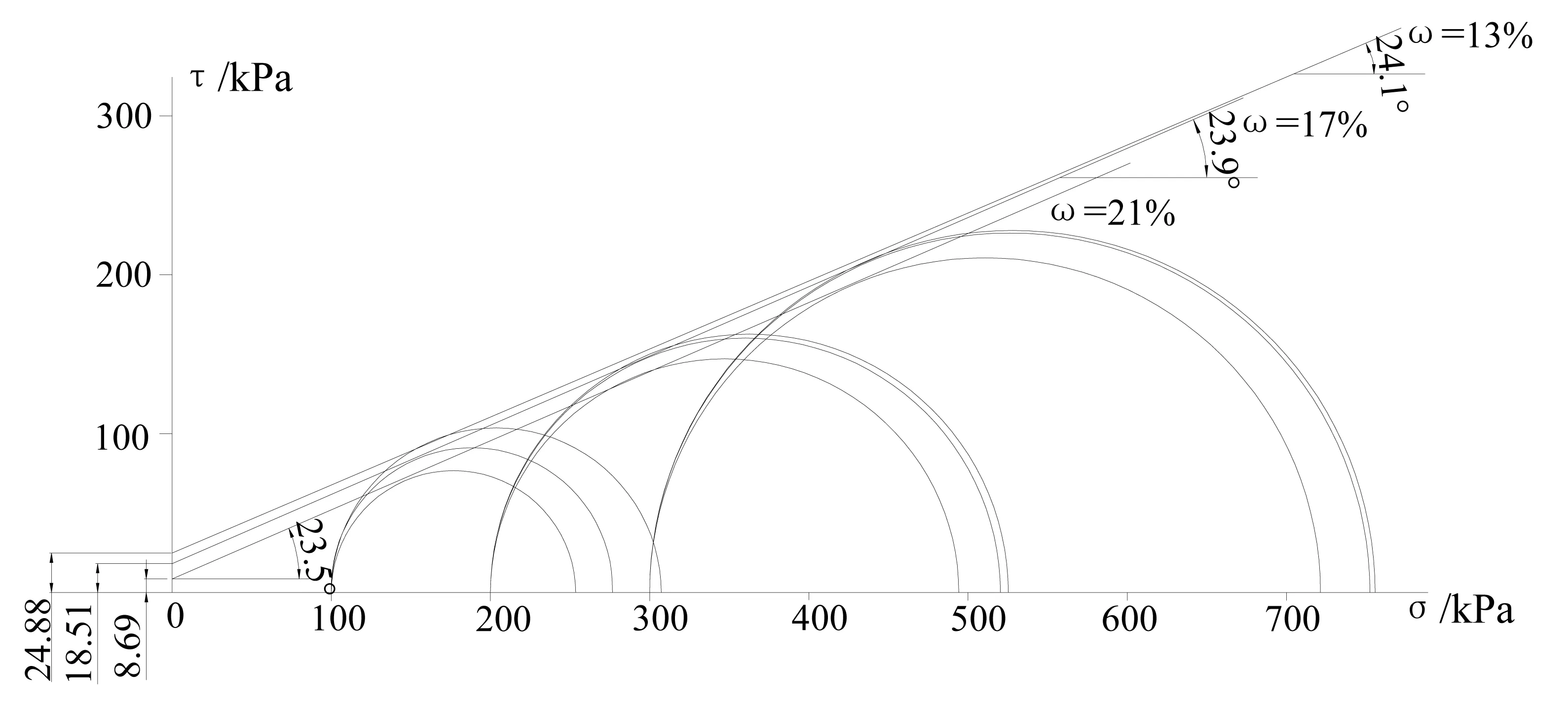
圖2 三軸剪切摩爾強度包線Fig.2 The Mohr strength envelope of triaxial test

3 鄧肯-張模型參數確定

由圖1可見，花崗巖殘積土試樣的應力～應變曲線總體上呈非線性的加工硬化型，與鄧肯-張模型的條件式(1)基本吻合，但在小應變階段試驗數據大多不太正常。式(3)～(6)中共有5個模型參數，即c、φ、K、n、Rf，其中c、φ值按摩爾庫倫準則，根據圍壓σ3和破壞偏應力(σ1-σ3)f繪制強度包線獲得(圖2)。由圖2得：含水率13%時c、φ值分別為24.88 kPa、24.1°；含水率17%時c、φ值分別為18.51 kPa、23.9°；含水率21%時c、φ值分別為8.69 kPa、23.5°。模型參數K、n、Rf大小取決于試驗常數a、b，下面分別采用“全點法”和“兩點法”確定a、b值，然后進行比較分析。

3.1“全點法”求取。

所謂“全點法”就是將全部的(σ1-σ3)～ε1試驗數據，按式(2)進行線性化處理，并繪制擬合直線求得a、b值。將全部試驗數據線性化后得到散點圖，如圖3所示，可見除了在軸向應變較小(基本在3%以內)時，有一些散點分布異常、與理論位置偏差巨大外，同一試驗的其他散點基本分布在一條直線上。根據圖3所擬合的直線(略)，可確定“全點法”的試驗常數a、b及模型參數K、n、Rf，見表1。

圖3 “全點法”線性化散點圖 Fig.3 The linearization scatter plot of “All point method”

圖4 “兩點法”直線Fig.4 The straight line of “Two point method”

3.2“兩點法”求取。

所謂“兩點法”是提取應力水平S=70%和S=95%的線性化試驗數據，在ε1/(σ1-σ3)～ε1坐標系中作通過該兩點的直線，從而求得a、b值[7]。根據試驗數據所作的“兩點法”直線如圖4所示，依此求得的a、b值及模型參數K、n、Rf也列在表1中。

3.3 模型曲線擬合。

根據上述兩種方法得到的試驗常數a、b，按式(1)采用Matlab擬合出各試樣在不同圍壓下的應力～應變曲線，并與試驗曲線進行對比，如圖5所示。可見，除個別情況外，兩種方法在小應變時的擬合結果比較接近，但當軸向應變達到一定值后，“兩點法”的擬合曲線大部分幾乎和試驗曲線重合，而絕大多數“全點法”的擬合曲線明顯低于試驗曲線，因此“兩點法”的擬合精度明顯高于“全點法”。

表1 鄧肯-張模型參數及試驗常數對照表

從表1分析，“全點法”擬合結果總體偏小的原因是試驗常數b偏大。b值偏大，意味著偏應力的極限值(σ1-σ3)ult偏小，導致破壞應力比Rf偏大。再進一步究其原因，是由于受試驗的系統誤差及試驗操作等人為因素的影響，各試樣在低應力階段的應力應變關系均存在不同程度的異常。由于“全點法”使用了全部試驗數據，不可避免要受這些異常數據的干擾而影響精度，而“兩點法”僅使用高應力水平的兩組數據，不僅簡單、方便，而且避免了低應力階段異常數據的干擾。

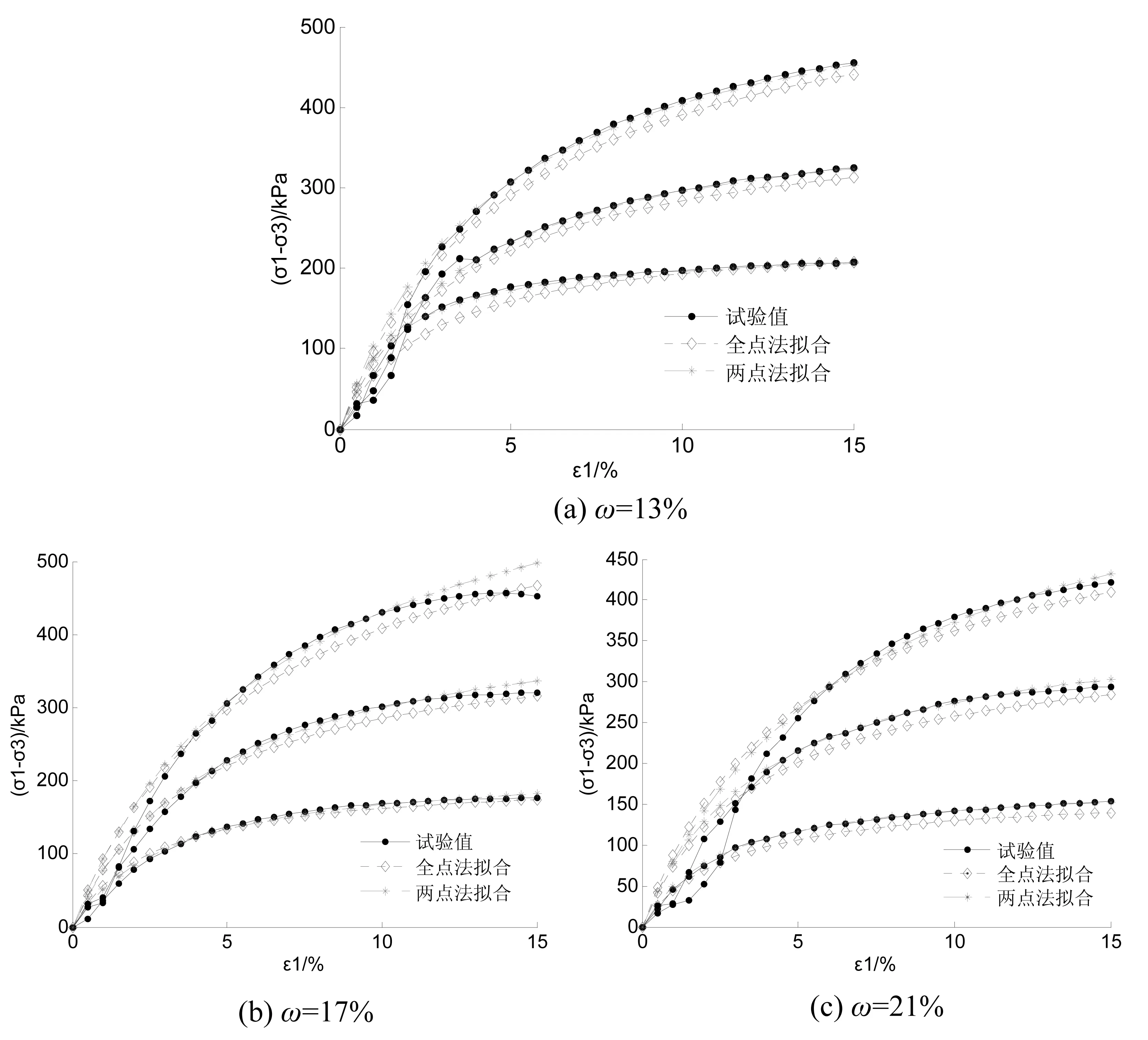
圖5 應力～應變曲線擬合

4 結語

為了提高巖土及地下工程分析計算的可靠度，除了所選用的巖土本構模型必須比較符合實際外， 關鍵在于計算

所用的模型參數的精度。研究表明，花崗巖殘積土的應力應變關系與鄧肯-張模型基本吻合，適宜使用鄧肯-張模型進行分析計算，但由于受試驗的系統誤差及試驗操作等人為因素的影響，試驗數據在低應力階段通常存在異常現象，因此若采用“全點法”確定模型參數，不可避免要受到異常數據的干擾而影響精度，而“兩點法”僅使用高應力水平的兩組數據，不僅簡單、方便，而且可以避免低應力階段異常數據的干擾，精度較高。為此建議采用“兩點法”確定花崗巖殘積土的鄧肯-張模型參數。

[1]吳能森，趙塵，侯偉生.花崗巖殘積土的成因、分布及工程特性研究[J] .平頂山工學院學報，2004，13(4)：1-4.

[2]張學言，閆澍旺.巖土塑性力學基礎(第2版)[M].天津：天津大學出版社，2004：60-65.

[3]徐中華，王衛東.敏感環境下基坑數值分析中土體本構模型的選擇[J].巖土力學，2010，31(1)：258-264.

[4]Kondner R L. Hyperbolic Stress-stain Response: Cohesive soils [J].Journal of the Soil Mechanics and Foundations Division. ASCE, 1963, 89( SM1): 115-143.

[5]Duncan J M, Chang C Y. Nonlinear analysis of Stress and Strain in Soils [J].Journal of the Soil Mechanics and Foundations Division. ASCE, 1970, 96(SM5): 1629-1653.

[6]GB/T 50123-1999 土工試驗方法標準[S].

[7]馮衛星，常紹東，胡萬毅.北京細砂土鄧肯-張模型參數試驗研究[J].巖土力學與工程學報，1999，18(3)：327-330.

ClassNo.:TU411DocumentMark：A

(責任編輯：宋瑞斌)

ReasonablyDeterminingtheParametersofDuncan-ChangModelforGraniteResidualSoil

Lai Rongzhou, Wu Nengsen, Xu Qing

(School of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002，China)

To determine Duncan-Chang model’s parameters of granite residual soil, three different moisture content samples were made and triaxial consolidation drained tests were done under surrounding pressures of 100 kPa、200 kPa and 300 kPa respectively. All stress-strain curves obtained are of the property of work-hardening which coincides with the conditional formula of Duncan-Chang model essentially. Afterwards, parameters of Duncan-Chang model were calculated to curve fit by means of “all point method” and “two point method” respectively, and the result is as follow: “all point method” is poor than “two point method” in accuracy, because “all point method” is interfered by abnormal data unavoidably; whereas “two point method” is not only simple and convenient, but can prevent from being disturbed by abnormal data in low stress level due to only using two sets of data in high stress level, so, It is suggested that “two point method” should be apply to calculate the Duncan-Chang model’s parameters of granite residual soil in engineering practice.

granite residual soil;Duncan-Chang model; triaxial test; all point method; two point method

賴榕洲，碩士，福建農林大學交通與土木工程學院。

吳能森，通訊作者，博士，教授，博士生導師，福建農林大學交通與土木工程學院。研究方向：巖土力學及地下工程。

福建省自然科學基金項目(2007J0357)；福建省高等學校科技項目(JA09073)；福州大學土木工程國家級實驗教學中心第三期創新性實驗研究項目(IRP2012-3)；福建農林大學創新(培育)團隊建設項目(Pytd12006)。

1672-6758(2013)12-0071-3

TU411

A