對2012年安徽中考物理卷兩道題目的質疑

王偉民

（安徽省太和縣宮集鎮中心學校，安徽 太和 236652）

就我國現在的教育體制來說，中考是僅次于高考的全國性“大考”（若論考生的數量，每年參加中考的人數比高考人數還要多），從每年中考期間各考點大門前由家長及帶隊教師組成的“送考大軍”即可見一斑.這就要求中考試卷應嚴把題目的科學性，試卷題目的編擬應發揚古人“吟妥一個字，拈斷數根須”的煉字精神，做到字斟句酌，科學嚴謹，無懈可擊.

然而，縱觀2012年安徽中考物理試卷，筆者以為，其中一些題目的編擬存在明顯的瑕疵.

例1.（2012年安徽中考物理試卷第7題）地球的表面積約為5.1×1014m2.地球表面的大氣壓約1.0×105Pa，則大氣對地球表面的壓力約為_______N.

不難發現，題目的編擬者想通過本題考查學生對壓力、壓強、受力面積之間關系式F＝pS的理解及運用能力.但是，編者沒有注意到，力是矢量，對壓力而言，只有物體各部分所受壓力方向一致時，物體所受的總壓力才等于各部分壓力的代數和.地球是個球體，地球表面各處所受大氣的壓力均指向地球的球心，地球上不同地方的大氣壓力方向不同，所以，即便知道地球的表面積和大氣壓強，也不可以利用公式F＝pS來計算大氣對地球表面的總壓力.若把地球看作一個標準的球體，并按照矢量的合成法則來計算地球表面所受大氣的總壓力，則總壓力數值應為0N（試卷“參考答案”給出的結果為5.1×1019N，顯然是根據公式F＝pS算出來的），而矢量與標量屬高中物理內容，初中生尚未學習，用這樣的題目來考查初中學生，雖說大部分學生可以“稀里糊涂”地根據公式F＝pS把所謂的“正確答案”做出來，但如此做法卻會給學生一種誤導——將矢量求和按標量求和的方法來對待，不要說這樣的方法錯誤，單是這種思維定勢對以后學生在高中物理及數學中的矢量求和內容學習，都將是非常不利的.

對初中生而言，本題可作如下修改——“中國的國土面積約為9.6×1012m2.若大氣壓約1.0×105Pa，則大氣對我國國土表面的壓力約為_______N.（我國的國土面積不到地球表面積的2%，可將其近似看作平面）”

例2.（2012年安徽中考物理試卷第9題）如圖1所示，利用動滑輪來提升一個物體，拉力F豎直向上.動滑輪其實就是一個變形的杠桿，請在圖中標出它的支點O，并畫出F的力臂L.

與定滑輪相比，動滑輪的特點是“雖然不能改變力的方向，但卻可以省一半的力”.需要說明的是，動滑輪的特點是“可以”省一半的力，但并非“一定”省一半的力.比如，用輕質滑輪來提升重物，在不計繩重及摩擦的情況下，若采用圖2所示的方法來提升重物，不但不能省一半的力，卻還要多費一倍的力，這就是說，對于變形杠桿動滑輪來講，動力臂未必一定為阻力臂的.

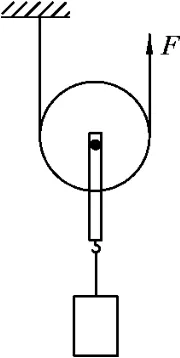
圖1

圖2

對杠桿而言，在幾個力的作用下，杠桿若保持平衡，則這幾個力的大小不會因所選擇支點的改變而變化.換句話說，對杠桿來講，支點的選擇可以是任意的.只不過在一般情況下，人們為了方便解決問題，通常選擇某個力的作用點作為支點，這樣，該力的力臂為零，該力的大小不會對杠桿的轉動產生影響，討論問題或求解某個未知量會比較方便.

我們以杠桿受力最簡單的一種情形為例，來證明支點的選擇不影響各力的大小.

如圖3，設輕質直杠桿OAB，選擇O為支點時，除支點O外，杠桿受兩個與杠桿垂直的力F1和F2的作用而保持平衡，設OA＝l1，OB＝l2，利用杠桿的平衡條件.則有F1l1＝F2l2.

圖3

圖4

當所選支點位置改變時，比如，我們將所選擇的支點向左平移k個單位至O′點（O′點不在杠桿上，是空間的另一個點），如圖4，因為F1＞F2，根據平行力的合成法則，杠桿平衡時，原支點O點處將受到一個方向向下，大小為F3＝F1－F2的力.對新支點O′而言，3個力的力矩之和為

用同樣的方法，我們可以證明，受n個力作用的杠桿，若相對于某支點，這n個力的力矩之和為0（即杠桿保持平衡），則將支點作任意變換時，相對于新的支點，這些力的力矩之和仍為0.

這就是說，對已平衡的杠桿來說，不論支點選在何處，都不會影響各力間的大小關系.因此，運用杠桿的平衡條件求解相關的未知量，支點的選擇可以是任意的（實際上，杠桿繞支點的轉動屬于機械運動，支點即為機械運動中的參照物，而機械運動中，參照物的選擇可以是任意的，所以，研究杠桿的轉動時，支點的選擇也應該是任意的）.

8讓我們再回到例2，圖1中，若不考慮滑輪的自重，動滑輪將受3個力的作用：兩邊繩子向上的拉力及所掛重物對滑輪向下的拉力，設繞過滑輪的繩子左邊拉力為F′，右邊拉力為F，重物對滑輪的拉力是G，則欲研究F與F′的大小關系，選擇滑輪的軸心作為支點比較方便（該題絕大多數失分考生的“錯誤”原因，是因為將支點選在了軸心，從而與“參考答案”不同造成的）；欲研究G與F′的大小關系，選擇滑輪的右側與繩子的切點處作為支點較為合適；而只有研究F與G的大小關系時，選擇滑輪的左側作為支點（即“參考答案”中的選法）才比較方便.需要注意，我們說的僅僅是“方便”，并非“必須”.實際上，在研究滑輪所受各力間的大小關系時，選擇其他任何一點作為支點都是可行的，只不過支點選擇得合適，研究或計算比較方便，支點選擇不合適，會給計算帶來很大的麻煩.我們不妨對此加以證明.

圖5

如圖5，在空間內任選一點O作為支點，過O作變形的杠桿動滑輪所受3個力F′、F、G作用線的垂線，垂足分別為A、B、C，設滑輪的半徑為R，OA＝x.

（1）研究F與F′的大小關系.

由杠桿的平衡條件得

由平行力的合成法則得

將（2）式代人（1）式得

即 F′x＋F′R＋Fx＋FR＝F′x＋Fx＋2FR，

所以有 F′R＝FR，

即 F′＝F.

（2）研究F與G、F′與G的大小關系.

這就是說，對于一個給定的動滑輪來講，不論選擇空間內的哪一點作為支點，根據題目條件，均可以求出兩個力間的大小關系.

對動滑輪而言，研究滑輪所受各力間的定量關系時，既然支點的選擇可以是任意的，而且根據題目所給條件，不論選擇哪一點作為支點都能確定兩力間的大小關系，那么，例2中要求考生“在圖中標出它的支點O”的做法顯然是多余的（不論標在哪里，也應該都算對的），緊接著“并畫出F的力臂L”的要求，其答案也不應是唯一的，而編者的“意圖”（從“參考答案”可以“揣摩”出題目編擬者的意圖）是想讓考生選擇圖中的“特殊”點，即滑輪的左側作為支點，相應的滑輪的直徑為力F的力臂，本應為“多姿多彩”的答案現在倒成了“唯一”的選擇.這樣的做法，對那些因中考答題與“參考答案”不同而失分的考生非常的不公平.

就目前的教育體制而言，中考仍是公眾重視程度很高的選拔性考試，而且，中考面向的是數以萬計的考生，規模之大是其他任何選拔性考試都無法相比的，中考題目的編擬，應該慎之又慎.