并列雙圓柱渦激振動的經驗性模型研究

秦 偉，康 莊，孫麗萍，宋儒鑫

(哈爾濱工程大學 船舶工程學院深海工程技術研究中心，黑龍江 哈爾濱 150001)

由于圓柱體之間的相互影響，雙圓柱體的渦激振動機理及現象相對于單圓柱體而言更加復雜。目前，國內外的研究者對雙圓柱體的渦激振動機理和現象進行了一定的研究，發現了影響串列或并列排列雙圓柱渦激振動特性的主要參數，比如兩圓柱體的中心間距、雷諾數以及兩個圓柱體的約束方式等。

Zdravkovich［1］對雙圓柱的渦激振動受力特性以及尾流形式做了綜述性的介紹，同時指出:對于雙圓柱體，由于兩個圓柱周圍流場的相互影響作用，在同一雷諾數下，也會表現出和單個孤立圓柱體不同的振動特性和旋渦脫落現象，而且隨著橫向和流向間距比的不同，兩個圓柱體的尾渦特性和受力特性也會有較大的不同。姚熊亮［2］對均勻流中并列剛性和彈性圓柱的流場進行了分類，同時認為脈動升力和阻力系數與柱的振幅、約化阻尼及兩柱間距有關，對柱型結構而言，合理的響應預報模型取決于流體載荷的系統分析。Williamson［3］對并列雙圓柱體的尾流特性做了深入的研究，發現兩個圓柱體在T/D ＞2.2 的特定間距比條件下，并列雙圓柱體下游的尾渦域內存在平行渦街同步的現象，即兩個平行渦街表現為反相位(in anti-phase)或者是同相位(in phase)這兩種形式。Sumner［4］也對并列雙圓柱體尾渦進行了研究，發現其尾渦模態可能存在3 種形式，分別為單一渦街(Single-bluff-body behaviors)、偏向流動(Biased flow pattern)和平行雙卡門渦街(Parallel vortex streets)形式。具體每個影響區域的中心間距會隨著雷諾數、實驗條件和固定方式等的不同而發生一定的變化。Wang［5］發現當并列排列的兩個圓柱體之間的中心間距比為1 ＜T/D ＜1.1 ～1.2 時，兩個圓柱體可以基本看成一個圓柱體，出現單個卡門渦街。Sumner［4］研究發現在雷諾數Re=1 000 ～3 000，中心間距比T/D=1.5 時，出現了偏向流動的現象，圓柱體出現不對稱的尾流運動和高頻率的旋渦脫落模態，其中一側的尾渦脫落頻率是另一側的脫落頻率的倍數關系，同時Sumner 還指出在T/D =2.5 和T/D =4.5 時發現了并排雙卡門渦街現象，此條件下兩個圓柱體相互影響比較小，同時兩圓柱體的旋渦脫落頻率相當。

由于渦致雙圓柱振動的過程比單圓柱情況更加復雜，公開發表的有關預報雙圓柱渦激振動響應的經驗性模型十分有限。Facchinetti 等［6］采用尾流振子模型對串列排列的雙圓柱渦激振動進行描述，得到的計算結果能夠在定性和定量上與實驗和數值模擬結果保持一致。

本文主要研究二維并列雙圓柱的渦激振動，同時建立一個能夠預測結構渦激振動響應的經驗性模型:由于特定間距比條件下的旋渦脫落頻率出現分支，因此假設用兩個具有不同固有頻率(即斯特勞哈爾頻率)的尾流振子來描述流體對結構的非線性動力作用，同時兩個流體振子均滿足van der Pol 方程，進而得到了結構振子和流體振子的耦合方程組，聯立組成并列雙圓柱渦激振動的尾流振子模型。采用實例基本數據，對經驗性模型進行了數值求解，并與實驗測量值進行對比分析，結果表明模型預報的響應能夠很好地預計并列雙圓柱渦激振動的結構振動特性和一般規律。

1 并列圓柱尾流振子模型

1.1 結構振動方程

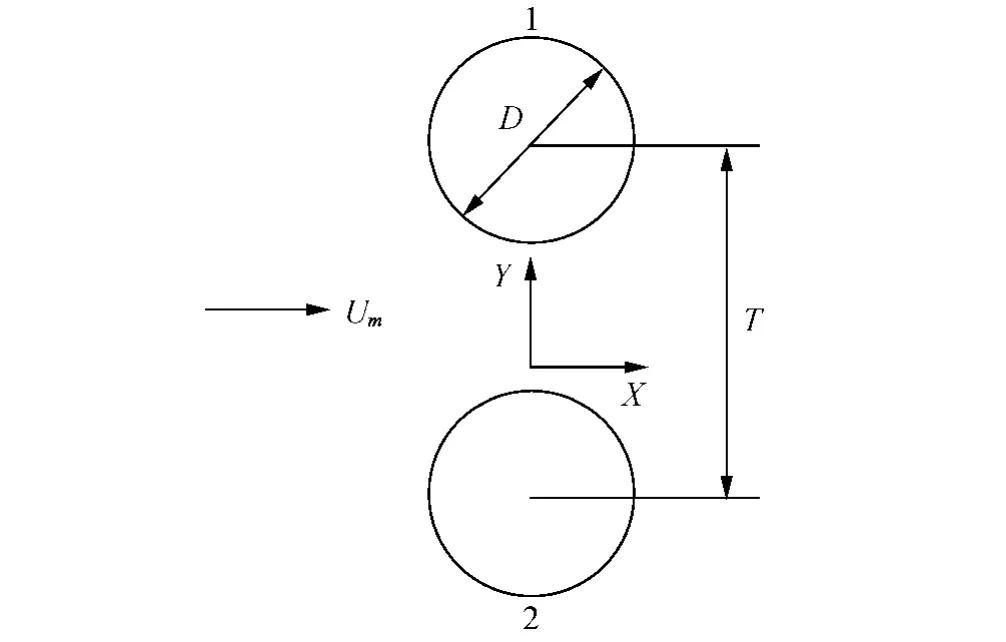
圖1 橫向并列圓柱布置Fig.1 A schematic layout of two side-by-side cylinders in a cross-flow

二維并列雙圓柱系統的布置如圖1 所示。兩個圓柱的直徑均為D，圓心之間的間距為T，同時考慮在流速為U∞的均勻來流作用下，圓柱沿垂直流向的橫向(Y 軸)運動。Facchinetti 等［7］給出了孤立彈性支承剛性圓柱的結構振動方程，對其進行拓展可以得到雙圓柱系統的結構振動方程為:

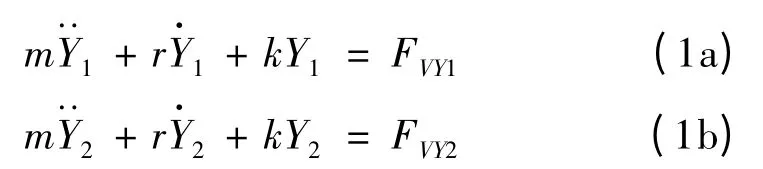
式中:m=(ms+ma)，ms為結構的質量，ma為流體的附加質量表示無粘流體的慣性作用力;ma=CaπD2ρ/4，Ca為流體的附加質量系數;r =(rs+rf)，為結構粘性阻尼;rf為流體附加阻尼，表示流體的粘性作用力;k 為結構的剛度;Y1和Y2分別表示圓柱1 和圓柱2 的橫向位置坐標，分別為結構橫向運動速度和加速度;FVY1和FVY2分別表示脫落的旋渦對圓柱1 和圓柱2 的脈動升力，通常將升力定義為無量綱的升力系數形式，即FVY1=ρU2DCL1/2 和FVY2=ρU2DCL2/2。

1.2 尾流振子方程

尾流振子方程將結構近壁的尾渦動力特性通過非線性振子來模擬，例如采用van der Pol 方程或者Rayleigh 方程來描述其自激自限的諧振動過程，并與結構振子聯立構成方程組，共同預測流固耦合系統的響應。Bishop 和Hassan［8］首先提出采用一個非線性自激的振子來表示作用在圓柱體上的升力。Hartlen 和Currie［9］以升力系數作為van der Pol 方程的狀態變量，給出了尾流振子方程的數學表達式。國內外諸多學者補充并推廣該方法，主要應用于研究孤立圓柱體，海洋立管和管道的渦激振動，如郭海燕［10］。

根據尾流振子模型建立的基本方法，引入無量綱參數q =2CL/CL0(其中的CL0為參考脈動升力系數［6］)為尾流振子方程變量，同時滿足受強迫激勵的van der Pol 方程，其中強迫項表示結構對流體振子的耦合作用。與單圓柱情況不同，并列圓柱的間距比對斯特勞哈爾數可能存在影響，圖2 給出了斯特勞哈爾數隨間距比變化的函數關系，可以看到尾渦模態為偏向流動情況下，可能存在兩個不同的主斯特勞哈爾頻率。因此，假設在特定的T/D 范圍內，流場中存在兩個具有不同固有頻率的尾流振子，其表達為:

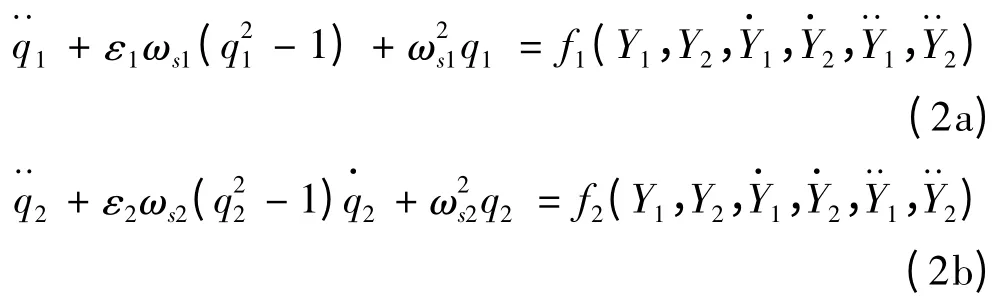
式中:ε 為van der Pol 方程參數;q1和q2分別表示圓柱1 和圓柱2 的尾流振子變量;ωs1和ωs2分別為圓柱1和圓柱2 相對應的旋渦脫落頻率，同時也是流體振子的固有頻率，其與斯特勞哈爾數的關系表達為ωs1，2=分別為耦合項。

Facchinetti 等［7］充分研究了單圓柱情況下結構與流體振子的耦合作用，分別對位移、速度、加速度三種耦合形式進行了對比和討論。研究表明強迫項采用結構的加速度形式最為理想，能夠反映共振特性，因此本文中采用的形式寫為:

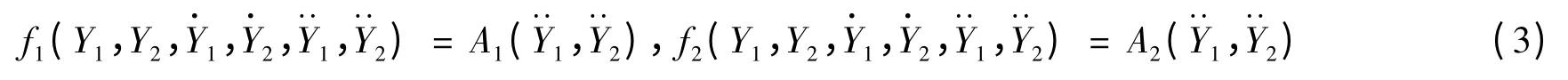
其中:A1和A2為實驗參數。

因此，脈動升力系數可以表示為:

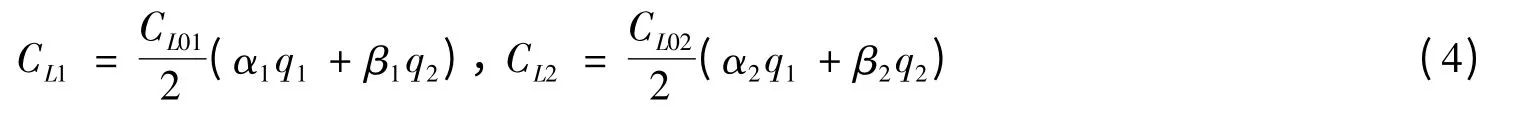
其中:(α1，β1，α2，β2)為模型的經驗性參數，分別是間距比T/D 的函數并滿足:

1.3 耦合振子模型

通過對結構振子方程式(1a)和式(1b)以及尾流振子方程式(2a)和式(2b)進行無量綱化，同時分別引入無量綱時間τ=(k/m)1/2t 和無量綱坐標y =Y/D，最終得到橫向并列雙圓柱的衰減階(Reduced-Order)耦合振子模型為:

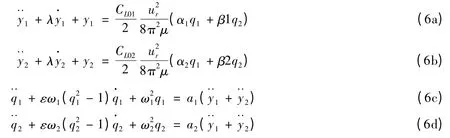
其中:此處的導數理解為對無量綱時間τ 求導;(α1，β1，α2，β2，a1，a2)為引入的無量綱參數;λ =r/(mk)為總阻尼比;ωn= (k/m)0.5為結構的固有頻率;μ = m/ρD2為質量比;ur= U/fnD 為來流的約化速度;ω1，2=ωs1，2/ωn為頻率比。

模型中的部分參數可以借鑒Facchinetti 等［7］尾流振子模型參數確定，本文中取a1=6，a2=6，ε =0.3。尾流振子方程中的頻率ω1和ω2分別代表旋渦的脫落頻率，需要根據不同尾渦模態中St隨間距比的變化規律來確定。參考脈動升力系數CL01和CL02一般是在固定圓柱條件下測得的，通常與雷諾數Re 有關。模型的經驗性參數(α1，β1，α2，β2)需要根據已有大量實驗數據通過曲線擬合或最小二乘法確定其函數變化規律，由于現階段可用的實驗數據有限，因此這些參數在具體實驗中給出。

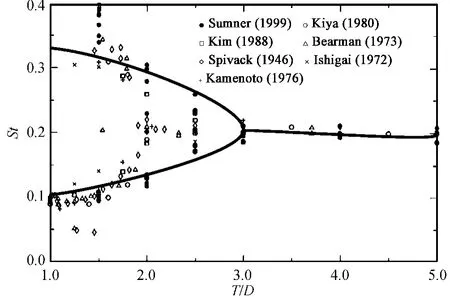
圖2 斯特勞哈爾數與間距比T/D 的關系Fig.2 Strouhal number data as a function of transverse pitch ratio T/D

2 計算實例與結果分析

2.1 實例基本數據

文中對比分析的數據來源于Liu 等［11］中高質量比并列雙圓柱的數值模擬實驗結果和低質量比的并列排列雙圓柱的模型實驗測量結果。

Liu 等對不同間距比條件下的并列雙圓柱進行了有限元CFD 數值模擬。分析中選取了三組不同的間距比，分別為T/D=1.8、3.0 和1.1。前兩種工況的設計參數為:無量綱質量比m*=4ms/(ρπD2)=10，質量阻尼比m*ξ=0.3。而在工況T/D=1.1 條件下，兩圓柱之間的距離很小，為了避免圓柱相撞需要調整結構的質量，其相應的設計參數取為無量綱質量比為m*=66，質量阻尼比為m*ξ =2.0。約化速度均控制在ur=5.0，相應的雷諾數為Re=200。

低質量比并列雙圓柱的模型試驗在船模拖曳水池開展。船模拖曳水池長108 m，池寬7 m，水深3.5 m。拖車車速0 ～6.5 m/s，拖車測量橋在垂直方向上的可調行程為0.4 m。實驗中使用的管模型為圓柱體，采用的材料為硬聚氯乙烯(UPVC)，直徑10 cm，壁厚5 mm，管長1.0 m，管底部有配重，兩端用水密封頭密封。模型的輔助設備包括與拖車固定的框架結構和與圓柱管相連的可擺動連桿架結構組成，圖3 給出了實驗模型的裝置圖和三維仿真模擬圖。實驗的相應設計參數包括，無量綱質量比m*=1.4，質量阻尼比m*ξ =0.047 6。約化速度的范圍在ur=4.2 ～16.8，相應的雷諾數范圍為Re=2 ×104～8 ×104。

圖3 并列雙圓柱實驗模型和實驗三維仿真模擬Fig.3 The experimental model for two side-by-side cylinders and 3-D simulation

2.2 模型的數值求解

并列雙圓柱的尾流振子模型即式(6a)～(6d)的數值求解使用的是自適應步長的四階龍格-庫塔方法。為了得到無量綱振幅與約化速度的關系，分別對增加流速和減小流速兩種情況進行計算，其流速增量的大小取為0.01，同時需要滿足后一流速條件下的初始條件取為前一流速的最終結果。時域模擬的時間控制為至少50 個振動周期，取穩定后的結果進行傅里葉分析從而得到振動的幅值與頻率。

Liu 等［11］首先對不同間距比條件下的固定并列雙圓柱進行了數值模擬實驗，實驗中可以測得參考脈動升力系數(CL0)和旋渦脫落頻率，為本模型中經驗性參數的確定提供參考。圖4(a)和4(b)分別給出了參考升力系數和模型中的經驗性參數隨間距比的變化規律。

在T/D=3.0 工況下，Liu 等得到了彈性并列雙圓柱的橫向位移(Y/D)響應隨時間的變化，如圖5(a)。結果顯示，兩個圓柱的位移響應均為一般的簡諧運動曲線，而且兩者之間的振動互為反相位。根據已確定的模型參數，對本文模型的方程組(6a)～(6d)進行數值求解，圖5(b)給出了經驗模型的預報結果，兩個圓柱的位移響應均為簡諧曲線，而且相位相差半個周期，即互為反相位。對比Liu 等［11］的實驗值，可以看到經驗模型預測的振動頻率與其吻合很好，但振動幅值偏小。

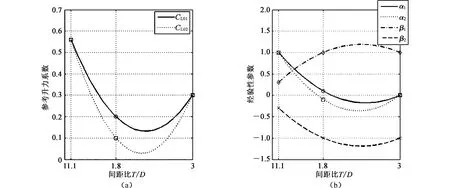
圖4 參考升力系數和經驗性參數隨間距比的變化規律Fig.4 The reference lift coefficients and the empirical parameters versus spacing ratios

在T/D=1.8 條件下，相應的尾渦形為偏向流模式(biased flow pattern)。Liu 等的實驗得到的升力和阻力時序曲線表現為強烈的不規則性，他們將產生的原因歸結于尾渦的相互作用，而非轉換性質(transition behavior)。同時，實驗中監測出升力CL 譜存在兩個主脫落頻率。圖5(c)給出了Liu 數值實驗得到的圓柱位移響應，可以看到響應曲線表現為不規則性。與此不同，經驗模型預報的圓柱振動中存在“拍”，即表明流體振子的一個頻率與結構的固有頻率相接近，如圖5(d)所示。因此，實驗中表現的強不規則性可能還包含了流－固之間的耦合作用。

當間距比取為T/D =1.1 時，兩個圓柱之間的距離很近，通常圓柱的位移幅值隨質量比的增加而減小，因此選用大質量比來保證兩圓柱不會發生碰撞。Liu 等設m*=66，并給出了圓柱的位移響應曲線，如圖5(e)。從圓柱剪切層脫落的發展旋渦存在很強的相互作用，同時還受到間隙流的影響，導致位移響應中有另一個額外峰值，位移譜也顯示出存在兩個主頻率。圖5(f)給出了經驗模型的預報結果，其得到的振動頻率和幅值都與實驗結果一致。

2.3 低質量比響應分析

低質量比并列雙圓柱渦激振動的模型實驗分別對T/D=4.7，4.2，3.9，3.5，3.0 和2.6 共六種工況進行了研究和討論。圖6(a)和6(b)給出了在間距比T/D=2.6，約化速度ur=6.3 條件下圓柱1 和圓柱2 借助加速度傳感器得到的結構頂部橫向位移加速度結果，由于提取的信號中存在高頻噪聲，需要對其進行光順濾波處理，本文采用低通與高通濾波方式對原始數據進行處理［12］。濾波后的加速度結果通過數值積分可以得到橫向位移隨時間的變化曲線，如圖6(c)和6(d)所示。經過譜分析從而得到了響應的振幅和頻率，如圖6(e)，以及斯特勞哈爾數隨間距比的變化關系，如圖6(f)所示。

低質量比渦激振動的顯著特點是圓柱的位移響應幅值相對較大，因此有必要對圓柱體橫向無量綱最大振幅(Y/D)進行討論。數值求解經驗模型的方程組，式(6a)～(6d)，其中參考升力系數取為經驗值CL01=CL02=0.3，模型的其它經驗性參數的取值及其隨間距比的變化規律在圖6(g)中給出，對比中高質量比的經驗性參數(圖4)，可以看到兩者的變化趨勢相近。

圖6(h)給出了T/D=4.7 和單圓柱條件下，模型實驗得到的圓柱最大振幅與約化速度的變化關系。可以看到并列雙圓柱的振幅響應及峰值位置與單圓柱的測量結果接近，因此可以認為兩個圓柱之間的距離較遠，相互之間的影響較小。經驗模型的預報結果與實驗結果的趨勢一致，振幅峰值都出現在約化速度ur=6.3附近，隨后最大振幅逐漸減小，但是預測的峰值數值偏小。

圖6(i)給出了T/D=2.6 條件下，模型實驗得到的圓柱最大振幅與約化速度的關系。實驗中發現圓柱的振幅響應在隨約化速度變化的過程中出現了兩個峰值，分別是在約化速度ur=6.3 和12.6 附近，其產生的原因可能是由于該間距比條件下結構所受的流體力存在兩個主頻率，隨著流速的增加兩個主頻率分別激起結構的共振從而出現兩個峰值。經驗模型也預報出兩個振動峰值，出現的位置和數值均小于實驗的觀測結果，但是最大振幅隨約化速度的變化趨勢與實驗結果基本一致。

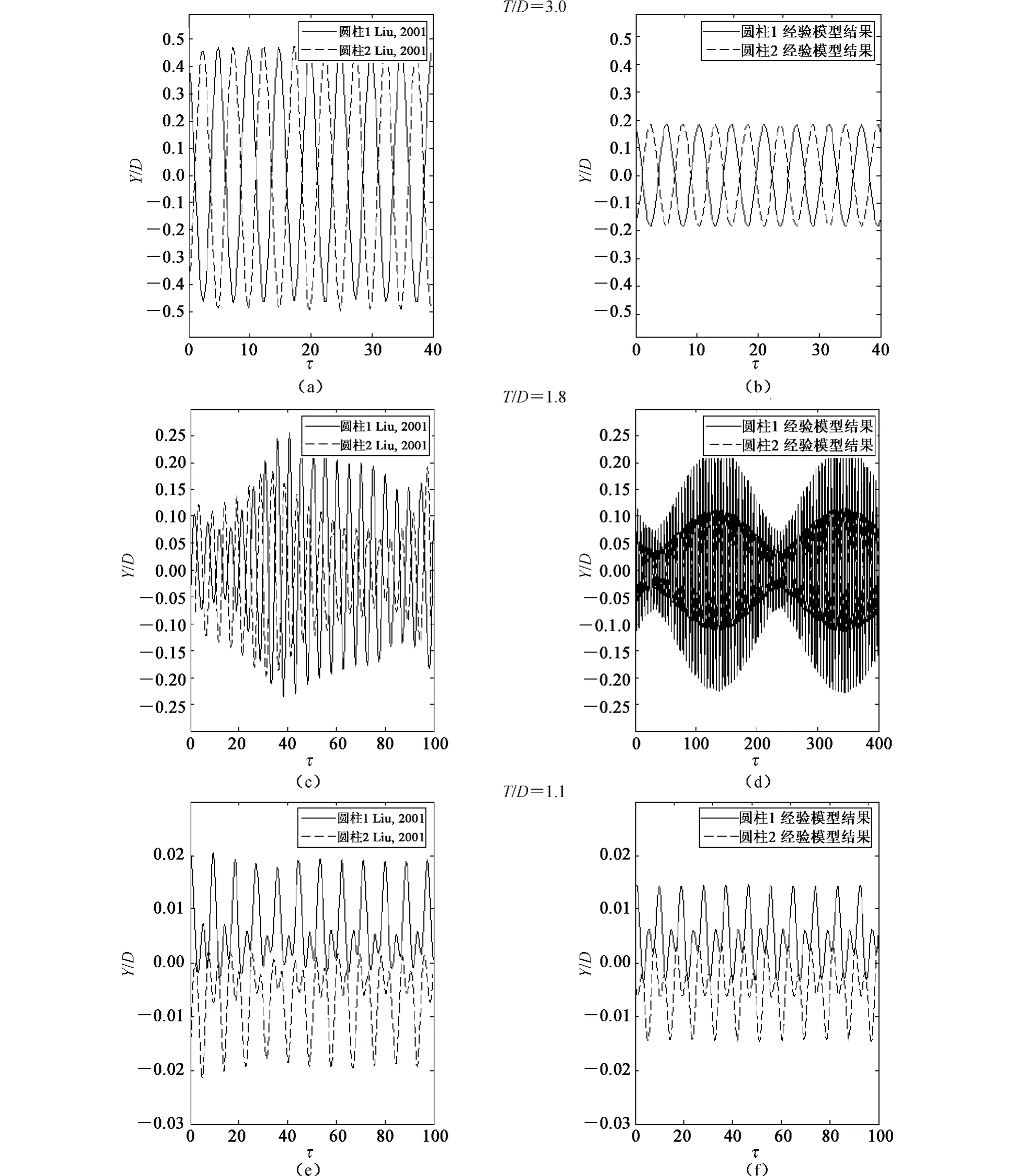
圖5 不同間距比條件下數值模擬和經驗性模型得到的Y/D 隨時間的變化Fig.5 Y/D time series for numerical simulation and empirical model under different spacing ratios

3 結 語

本文主要針對并列雙圓柱的渦激振動，建立了一種新的尾流振子模型，用來預測結構的渦激振動響應。現階段的研究表明，在特定間距比條件下，旋渦的脫落頻率(或斯特勞哈爾頻率)出現分支，即可能存在兩個主脫落頻率。因此，本文提出以兩個具有不同固有頻率的尾流振子來共同描述結構的近壁尾渦動力特性，同時兩個流體振子均滿足van der Pol 方程，進一步推導出結構振子和流體振子耦合的方程組，用來模擬并列雙圓柱的流固耦合現象。

本文同時給出了經驗模型的數值求解方法，并結合Liu 等［11］的中高質量比數值模擬實驗和低質量比模型實驗提供的設計數據，對該經驗模型進行了數值計算，得到的預測結果與實驗結果進行了對比。分析結果表明，預測的結構位移響應和最大振動幅值等變化規律與相應的實驗結果趨勢一致，能夠反映并列雙圓柱渦激振動的結構振動特性和一般規律。

［1］Zdravkovich M M.The effects of interference between circular cylinders in cross flow［J］.Journal of Fluids and Structures.1987，1(2):239-261.

［2］姚熊亮，陳起富.均勻流場中并列圓柱渦激振動的現狀與預測［J］.海洋工程，1995，13(3):37-47.

［3］Williamson C H K.Evolution of a single wake behind a pair of bluff bodies［J］.Journal of Fluid Mechanics.1985，159:1-18.

［4］Sumner D，Wong S S T，Price S J，et al.Fluid behavior of side-by-side circular cylinders in steady cross-flow［J］.Journal of Fluids and Structures.1999，13:309-338.

［5］Wang Z J，Zhou Y，Li H.Flow-visualization of a two side-by-side cylinder wake［J］.Journal of Flow Visualization ＆ Image Processing，2001，9:123-138.

［6］Facchinetti M L，Langre E，Fontaine E，et al.VIV of two cylinders in tandem arrangement:analytical and numerical modeling［C］∥Proc. of the 12th (2002)International Offshore and Polar Engineering Conference.2002:524-531.

［7］Facchinetti M L，Langre E，Biolley F.Coupling of structure and wake oscillators in vortex-induced vibrations［J］.Journal of Fluids and Structures，2004，19:123-140.

［8］Bishop R E D，Hassan A Y.The lift and drag forces on a circular cylinder in a flowing fluid［C］∥Proc.of Royal Society Series A，1963，277:32-50.

［9］Hartlen R T，Currie I G.Lift-oscillator model of vortex-induced vibration［J］.Journal of the Engineering Mechanics，1970，96:577-591.

［10］Li Xiao-min，Guo Hai-yan，Meng Fan-shun.Nonlinear coupled in-line and cross-flow vortex-induced vibration analysis of top tensioned riser［J］.China Ocean Engineering，2010，24(4):749-758.

［11］Liu Y，So R M C，Lau Y L，et al.Numberical studies of two side-by-side elastic cylinders in a cross-flow［J］.Journal of Fluids and Structures.2001，15:1009-1030.

［12］張建僑，宋吉寧，呂林，等.柔性立管渦激振動實驗的數據分析［J］.中國海洋平臺，2009，24(4):26-32.